水面無人艇領航—跟隨固定時間編隊控制

李賀，王寧，薛皓原

大連海事大學 船舶電氣工程學院，遼寧 大連 116026

0 引 言

近些年，水面無人艇（Unmanned surface vehicle,USV）在軍民用領域扮演的角色越來越重要，其可遂行情報偵察、水域環境檢測、海圖繪制等任務[1]。但是，當面臨復雜的水域環境以及多樣性的作業任務時，單個USV顯得勢單力薄，而多USV協同控制因其具有效率高、覆蓋廣、魯棒性強等優勢，逐漸成為研究的熱點[2]。在多USV協同控制領域，研究熱點之一便是編隊控制，主要策略有：圖論[3]、基于行為的控制策略[4]、虛擬領航者[5]、神經網絡[6]和領航—跟隨控制策略[7]等。在上述幾種策略中，領航—跟隨控制策略具有控制結構簡單、可擴展性好等優勢，因而得到了更加廣泛的應用。該策略中，跟隨USV只需接收領航USV的動態信息，便能夠實現穩定的編隊隊形。

領航—跟隨USV編隊控制系統中，其穩定性將會受到復雜的外界環境擾動影響（主要為水域環境中的風、浪、涌等干擾），這給USV編隊的穩定控制帶來了極大的困難。滑模控制技術因其具有較強的抗不確定性和抗擾性，已經在隨機系統、剛體系統、海洋裝備等領域得到了較為廣泛的應用[8]。常見的滑模技術主要有傳統的漸進收斂滑模[9]、積分滑模[10-11]、終端滑模[12]、非奇異終端滑模[13-14]等。為了進一步處理復雜的外界擾動，以前的研究主要采用了如非線性擾動觀測器[15]、降維擾動觀測器[16]等。近些年，有限時間擾動觀測器（finite-time distribute observer, FDO）技術逐漸成為研究熱點，Wang等[17-24]對FDO進行了嘗試應用，取得了顯著的成果。相比于傳統的擾動觀測器，FDO能夠對擾動實現快速、精確的辨識。但是，FDO技術在USV編隊控制領域鮮有應用，具有潛在的研究價值。

在領航—跟隨USV編隊控制中，為了更好地保證編隊系統的響應特性，收斂速率是首要考慮的控制指標。早期的文獻針對一階多智能體系統的線性一致性拓撲，提出了代數連通圖的概念，并運用漸進收斂算法證明了其有效的收斂性[25]。然而，漸進收斂算法存在收斂時間不可預測的不足，導致了系統穩定性的不可預測。鑒于此，隨后的文獻更多采用有限時間收斂算法，求解單智能體或者多智能體編隊的收斂性問題[26-28]，該算法極大改善了以往算法的跟蹤精度和收斂速度。近幾年，作為有限時間算法的擴展，固定時間控制算法逐漸被引入多智能體編隊控制領域。固定時間控制算法由Polyakov[29]首次提出，該算法能夠實現有限時間收斂，并且其收斂時間的上界可以通過數學方法計算得到。Zuo等[30-32]在隨后的研究中分別運用固定時間算法在一階、二階以及高階多智能體系統中進行了嘗試應用，證明了其具有更好的精準性和收斂性。

基于此，本文將針對復雜擾動下的領航—跟隨無人艇編隊系統，提出基于固定時間的編隊控制策略。首先，設計基于積分滑模的固定時間跟蹤控制（ISM-FTC）策略，將其應用于跟蹤控制子系統中；然后，引入基于有限時間擾動觀測器的固定時間編隊控制（FDO-FFC）策略，將其應用于編隊控制子系統中，對復雜擾動下的領航—跟隨編隊系統進行精確控制；接著，通過Lyapunov函數證明所設計控制器的理論可行性；最后，通過仿真實驗，驗證所提出設計方法的可行性。

1 預備知識和問題描述

1.1 預備知識

引理1：對于非線性系統：

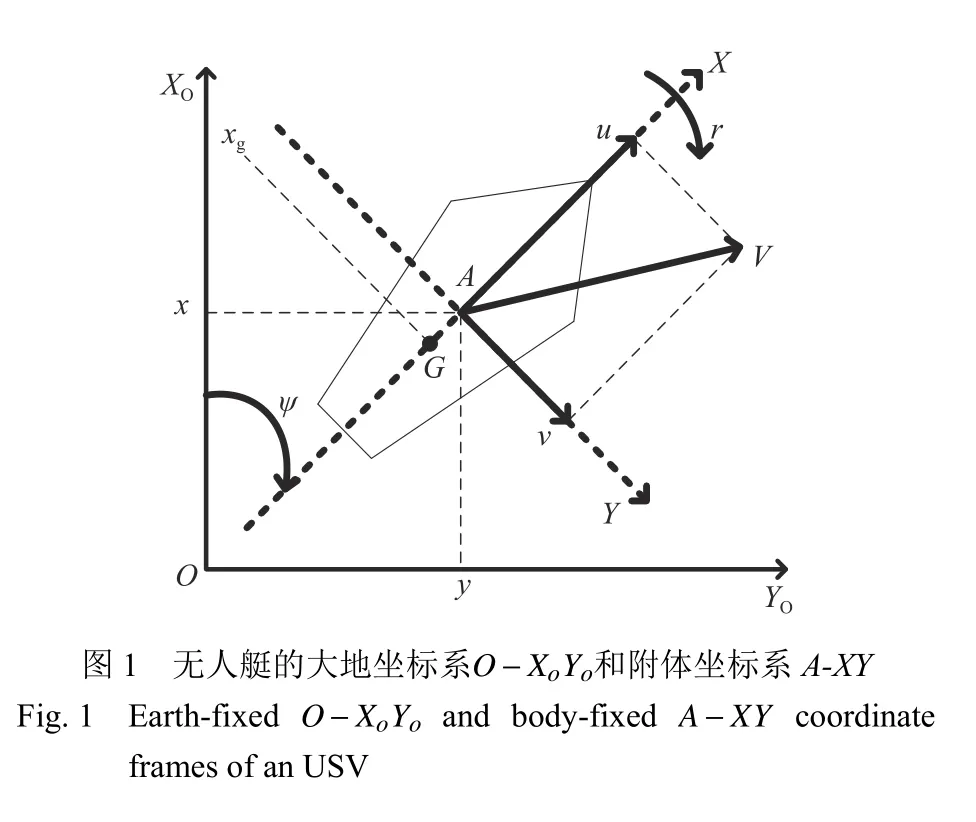
1.2 問題描述

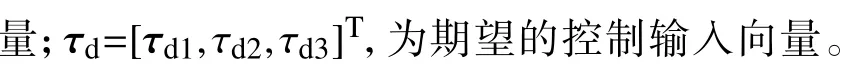
本文旨在設計一種固定時間編隊控制器，在固定時間內，控制器不僅能夠驅動跟蹤控制子系統精確跟蹤期望的軌跡，且能夠驅動編隊控制子系統快速形成期望的隊形并保持隊形，從而實現USV領航—跟隨編隊快速、精確的控制。

2 控制系統設計與穩定性分析

領航—跟隨編隊控制方案框圖如圖2所示，為保證編隊系統設計的整體性，將編隊系統劃分為跟蹤控制子系統和編隊控制子系統，分別設計控制器，從而保證編隊系統的有效性。

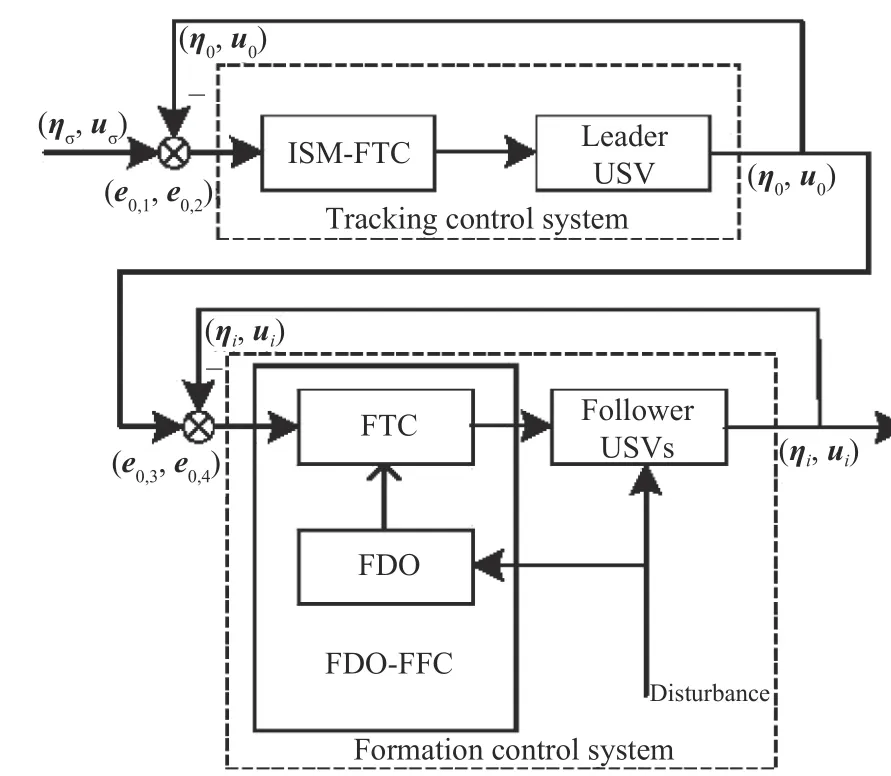
圖 2 領航—跟隨編隊控制方案框圖Fig. 2 The block diagram of the leader-follower control scheme

2.1 跟蹤控制子系統控制器設計

設計跟蹤控制子系統控制器，從而保證編隊系統對期望軌跡的精確跟蹤，同時為編隊控制子系統提供控制輸入信號。

2.2 編隊控制子系統控制器設計

3 仿真研究

為了驗證固定時間控制策略的有效性，利用經典的Cybership II試驗模型進行仿真實驗。設計1艘領航USV和2艘跟隨USV組成編隊系統，進行仿真驗證。

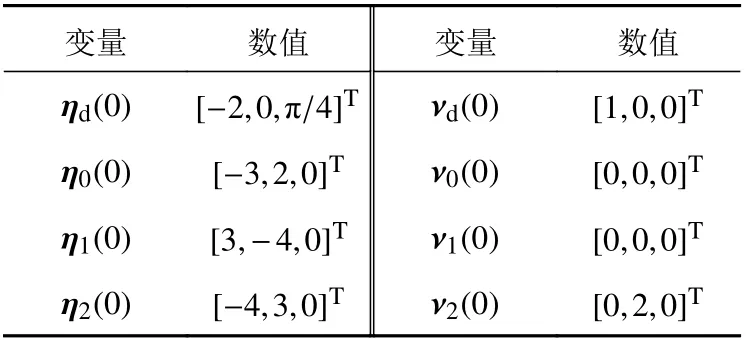
表 1 模型的初值Table 1 The initial values of the model

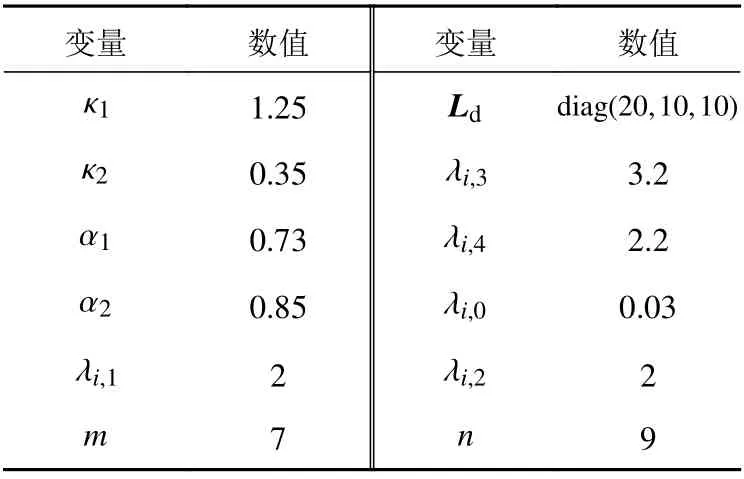
表 2 各參數的取值Table 2 The values of each parameter

仿真結果如圖3～圖12所示。圖3顯示了跟蹤控制子系統精確跟蹤的期望軌跡，可見編隊控制子系統能夠精確形成和維持領航—跟隨編隊隊形；圖4～圖5分別顯示了編隊系統的位置和速度跟蹤隨時間的變化曲線，可見在5 s內各個維度完成了期望的任務，并且收斂時間小于設定時間的上限；圖6～圖8分別顯示了領航USV和2個跟隨USV 的控制輸入隨時間的變化曲線，驗證了控制器能夠在固定時間內趨于穩定；圖9～圖10分別顯示了2個跟隨USV的外界擾動曲線以及FDO

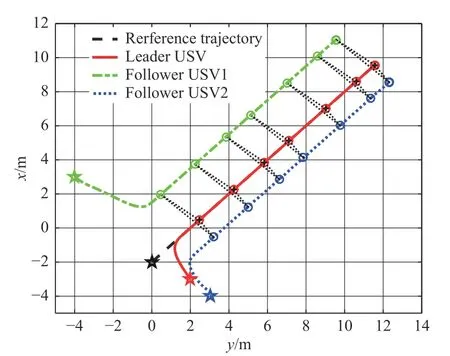
圖 3 USV編隊軌跡圖Fig. 3 The trajectories of USV formation

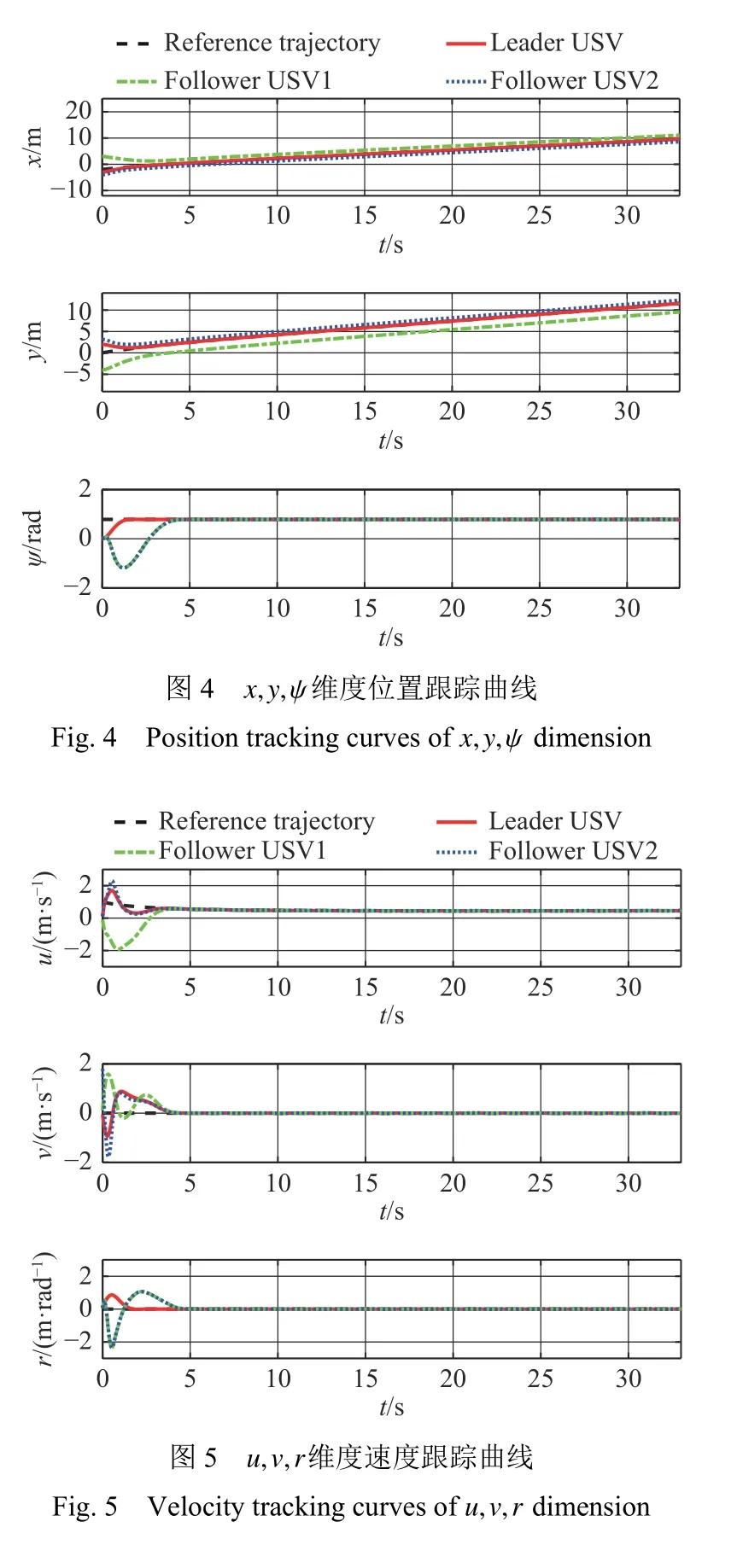
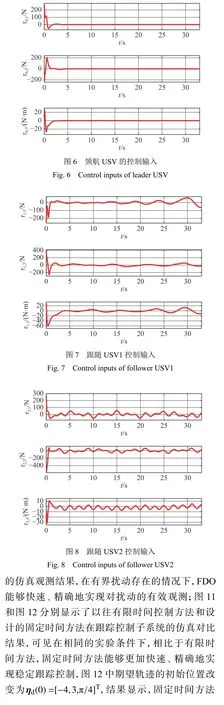
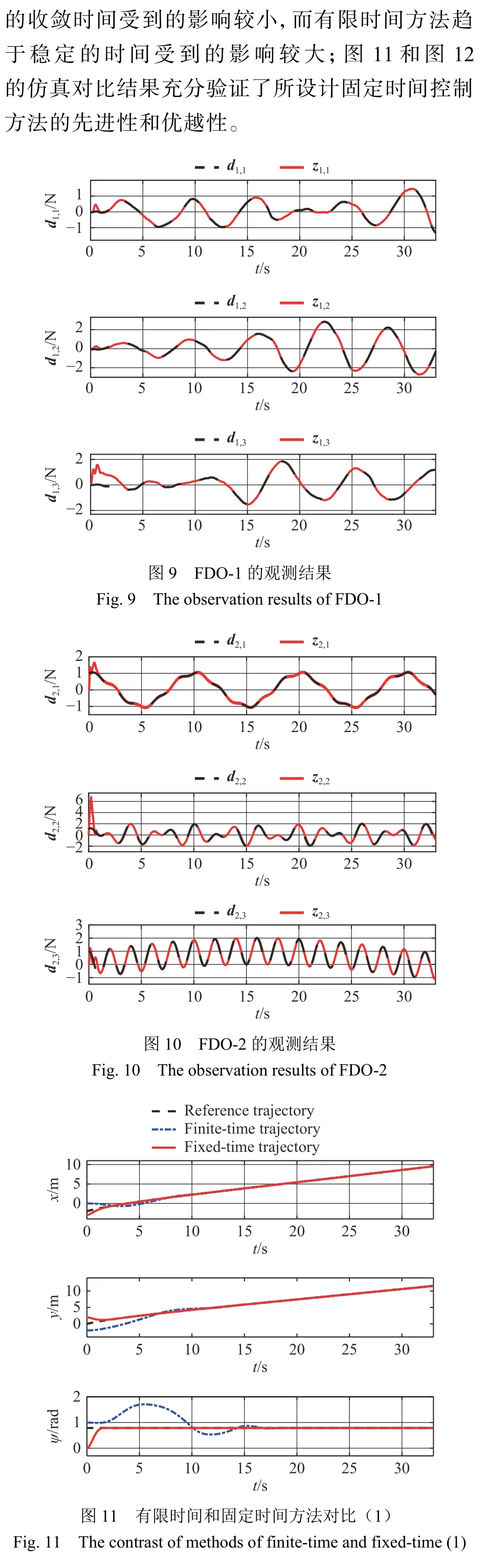
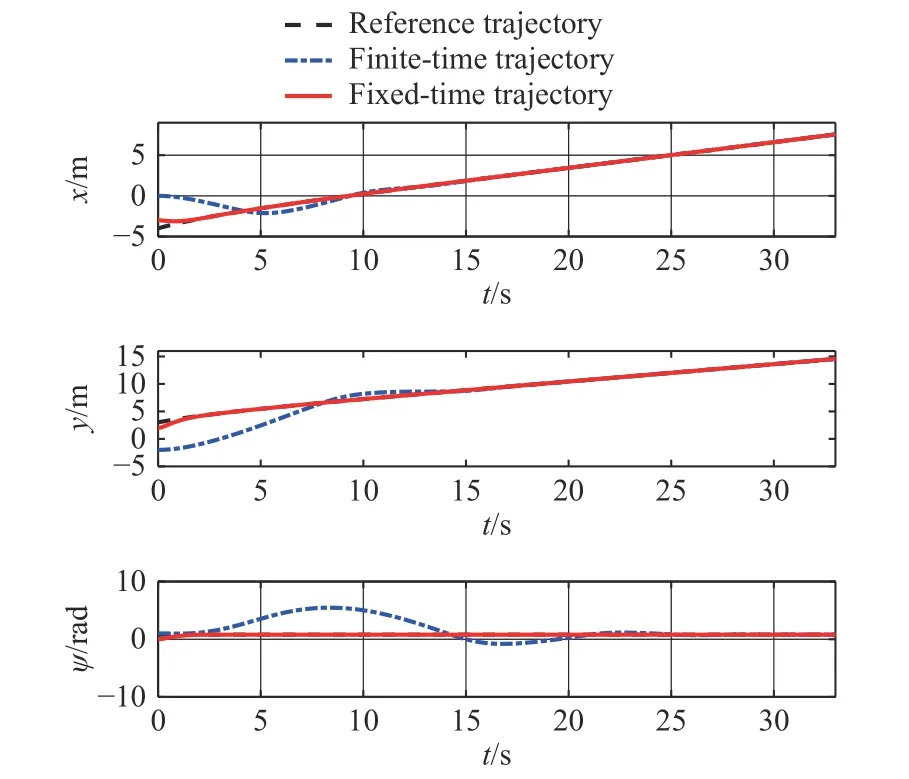
圖 12 有限時間和固定時間方法對比（2）Fig. 12 The contrast of methods of finite-time and fixed-time (2)

4 結 論

本文針對領航—跟隨USV編隊系統在復雜環境擾動下的控制問題，結合積分滑模和反步控制技術，提出了FTC策略。在跟蹤控制子系統中，設計了ISM-FTC控制器，使得領航USV精確跟蹤期望軌跡；在編隊控制子系統中，設計了FDOFFC控制器，使得跟隨USV精確保持對領航USV的相對位置，尤其是存在外界擾動的情況下，仍然能夠確保穩定的領航—跟隨USV編隊隊形。采用Lyapunov穩定性理論，證明了閉環編隊控制系統的穩定性。仿真結果表明，在復雜外界擾動下，所設計的USV編隊控制系統能夠精準跟蹤期望的軌跡并快速形成和保持期望的編隊隊形。本文設計的固定時間控制策略為USV編隊控制提供了新的設計方案。