基于EMD-LSTM耦合預測模型的BDS多路徑誤差削弱方法研究

徐小汶,陶 遠

(安徽理工大學 測繪學院,安徽 淮南 232001)

0 引 言

在北斗衛星導航系統(BDS)高精度變形監測中,通常采用相對定位的方式觀測. 其中,雖然采用雙差法可以完全消除衛星鐘差與接收機鐘差,也可憑借短基線測量中測站間距離較短的原因忽略電離層延遲與對流層延遲的影響,但多路徑誤差卻不能通過差分法消除,在BDS觀測數據中依然存在[1]. 因此,多路徑誤差成為高精度BDS應用的主要誤差源.

除合理的選址可降低多路徑誤差的影響外,削弱多路徑誤差的方法主要集中在接收機硬件和數據后處理兩方面. 從硬件方面削弱多路徑誤差,主要通過改進接收機天線的方式來抑制多路徑誤差,但其存在成本較高且消弱多路徑誤差效果較差的問題. 鑒于此,眾多學者采用數據后處理的方式削弱多路徑誤差,展開了一系列的研究. 其中應用最為廣泛的理論有如下幾種:基于信噪比方法或載噪比對全球定位系統(GPS)觀測值進行多路徑誤差削弱[2-3];基于多種濾波技術消除多路徑誤差,如基于交叉認證技術的Vondrak濾波[4]、經驗模態分解(EMD)方法[5-6]、小波分析[7]等. 雖然上述理論的研究取得了良好的效果,但上述后處理方法均是基于恒星日濾波技術進行應用. 而BDS具有星座異構的特點,其MEO衛星的回歸周期與地球靜止軌道(GEO)衛星、傾斜地球同步軌道(IGSO)衛星相差較大,因此在坐標值域中恒星日濾波方法將難以適用.

鑒于坐標值域序列優秀的后處理效率,同時針對BDS坐標值域中多路徑誤差難以適用恒星日濾波方法[7-8]以及神經網絡預測結果存在滯后性的問題,本文在深度學習方法的基礎上,提出采用EMD-LSTM的多路徑誤差預測模型進行多路徑誤差剔除. 本文的研究內容如下:首先基于EMD算法對多路徑誤差進行多尺度分解,然后利用長短期記憶神經網絡(LSTM)對模態分量進行建模預測,最終將預測值重構多路徑誤差,以此構建多路徑誤差的預測模型,實現多路徑誤差的準確改正.

1 多路徑誤差原理

在BDS測量中,衛星信號被測站周圍的障礙物影響,產生了反射或衍射現象. 這些干擾信號影響直射信號,從而使觀測值產生偏差或失真,這些干擾信號比直接信號有著更長的傳播路徑,導致產生傳播延遲,這種由多路徑的信號傳播所引起的干涉時延效應被稱作多路徑效應,這種效應導致的誤差為多路徑誤差. 多路徑誤差是BDS測量中一個重要的誤差源,多路徑誤差將嚴重損害BDS測量的精度,甚至將產生信號的失鎖[9].

由于多路徑誤差信號屬于載波信號,所以多路徑誤差具備與載波信號相同的性質,因此反射信號造成的多路徑誤差可簡單表示為

Sr=αAcos(φ+θ), 0≤α≤1，

(1)

式中:A與φ為反射信號的振幅與相位;α為反射因子；θ為多路徑誤差延遲相位. 多路徑誤差造成的相位誤差可表示為[10]

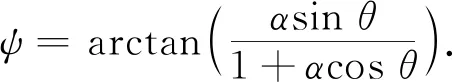
(2)

對于L1載波,多路徑誤差可使定位結果出現最大約4.8 cm的誤差.

對于短基線相對定位,多路徑誤差與測站環境、觀測衛星與接收機有關,當周圍環境變化較小或保持靜止時,每個運行周期為一個恒星日的衛星到接收機天線的幾何關系是相同的. BDS星座異構,坐標值域序列無固定周日重復性,難以對坐標值域進行恒星日濾波.

2 EMD-LSTM耦合模型

2.1 EMD原理

在處理BDS多路徑效應問題時,通常選擇對觀測數據進行降噪,以便最大程度上消弱多路徑誤差的影響. 本文選擇由Huang等[11]提出的經驗模態分解方法,也稱EMD算法. EMD算法的思想是:將BDS觀測數據看成是由一些互異的非正弦函數的信號分量構成. 依據這一特性,可以將復雜且波動較大的BDS觀測數據分解成若干個信號分量,并由高頻到低頻依次排列,這些信號分量稱為固有模態函數(IMF)[11-12].

針對BDS原始觀測序列x(t)的多尺度分解可以表示為

(3)

式中:imfi(t)為第i個多尺度分量;rn(t)為殘差余項.

EMD算法的實施步驟描述如下:

1)判斷BDS原始觀測數據x(t)中局部的極值點;

2)通過三次樣條插值函數獲得步驟1)中的局部極值點,并以此為基準構建觀測數據x(t)的上、下包絡線xu(t)和xd(t));

3)計算步驟2)中得到的xu(t)和xd(t)的平均值,其計算公式為

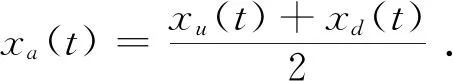
(4)

4)判斷q(t)是否滿足均值條件

q(t)=x(t)-xa(t).

(5)

若q(t)為零,此時可認為滿足要求并繼續進行運算;否則重復步驟1)～4),直至q(t)滿足均值條件;

5)提取BDS觀測數據中的殘余項ri(t),并判斷ri(t)是否滿足余項條件:

ri(t)=x(t)-imfi(t).

(6)

若極值點數ri(t)< 2,滿足余項條件,分解完成;若ri(t)> 2,則繼續按照上述步驟進行分解.

關于降噪問題的尺度選擇問題,常用的方法有以下幾種:①累積偏差法;②交叉認證法;③去除第一個IMF分量法;④依據通過分解后的IMF分量的能量密度與平均周期的乘積為常數值的特性,所設計的尺度選擇方法. 依據上述方法的便捷性與理論的嚴密性,本文選擇④中張敬霞[13]提出的一種自適應選擇IMF分量的算法,具體描述如下:

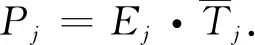
(7)

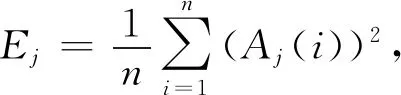
(8)

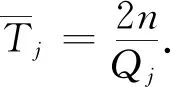
(9)

式中:Aj和Qj分別為第j個IMF分量的振幅和極值點的總和;n為每個IMF分量的長度.

2)計算RPj系數:

(10)

若RPj≥1,即認為所計算出的前j-1個IMF分量Pj為常數,將第j個IMF分量視為重構信號的尺度.

2.2 LSTM原理

長短期記憶網絡(LSTM)是Hochreiter和Schmidhuber在1997年所提出的一種特殊的深度學習方法,能夠很好地解決梯度爆炸和梯度消失問題,讓循環神經網絡具備更強更好的記憶性能. LSTM是使用獨特的“門”結構構建的,一般包括三個基本組件,分別是“忘記”,“輸入”和“輸出”門,三個組件協同工作以完成LSTM單元的功能并控制信息流[14].

在“忘記”門中,采用S型函數σ(*)記錄前一個狀態單元的儲存信息,表達公式如下[15]:

ft=σ(Wf[ht-1,xt]+bf),

(11)

式中:σ(*)為S形函數;Wf和bf為訓練后要確定的參數;ht-1為時間段t-1的隱藏狀態,xt為時間段t的輸入向量,ft為S型函數的輸出量.

函數的輸入量是前一個LSTM單元和輸入向量的隱藏狀態. 因此,函數的輸出量是介于0到1之間的值,并與前LSTM單元在單元狀態下的每個數字相對應. 這些值表示在先前單元狀態Ct-1中每個數字的遺忘度. 值“1”表示“完全保留”,相反,值“0”則表示“完全忘記或排除”[16].

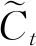
it=σ(Wi[ht-1,xt]+bi),

(12)

(13)

式中:σ(*)為S形函數;Wi,bi,Wc和bc為參數,將通過訓練過程確定,h為時刻t-1的隱藏狀態；xt是輸入向量.

最后,使用“輸出”門來決定和控制輸出. 此“門”由S型函數和tanh函數組成,表達公式詳見式(14)和(15). 其中,sigmoid函數的輸出量為Ot,它確定隱藏函數的輸出狀態,同時將單元狀態通過tanh函數并乘以向量Ot,用于確定LSTM單位的輸出.

Ot=σ(Wo[ht-1,xt]+bo),

(14)

ht=Ot*tanh(Ct).

(15)

式中:Wo和bo為訓練期間確定的參數;Ct為t時刻的細胞狀態.

2.3 EMD-LSTM的BDS多路徑誤差建模

在實驗中發現BDS多路徑誤差呈現高度非線性特征,且具有非平穩時間序列的特性.若將多路徑誤差分解為多模態分量,其各分量的非線性程度不但能夠降低,時間序列還會變得更加平穩,利于采用LSTM模型進行預測. 本文將EMD算法和LSTM方法相結合,構建一種基于EMD-LSTM耦合預測模型,對BDS坐標序列中的多路徑誤差進行預測,當獲取到對應歷元的數據時,對應改正其多路徑誤差.

基于EMD-LSTM耦合預測模型的流程圖如圖1所示,其削弱BDS多路徑效應的具體實施步驟如下:

1)對訓練數據多路徑誤差x(t)進行多尺度分解,分解成若干IMF分量;

2)根據式(10)計算RP系數,自適應舍棄高頻的噪聲IMF;

3)分別對有用信息的IMF分量進行LSTM預測;

4)預測分量重構多路徑誤差x′(t),改正實測序列.

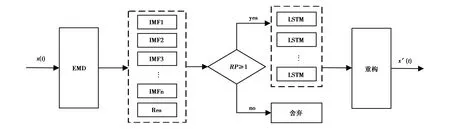
圖1 EMD-LSTM耦合模型流程圖

3 實驗與結果

3.1 數據來源

本實驗數據采集于安徽理工大學測繪學院五樓樓頂,由兩臺相同的接收機于2018-05-13-2018-05-15(共3天數據,年積日分別為DOY133、DOY134和DOY135)同時段接收BDS數據,采樣頻率為1 Hz,衛星截止高度角15°,接收機參數為天寶BD980板卡,AT300天線,支持BDS雙頻,且接收機采用扼流圈天線. 接收機間距離約為12 m,由于接收機距離較近,高程方向基本相當,可忽略對流層延遲、電離層延遲影響,并且天線相位中心偏差較小且穩定,因此測量型天線相位偏差對本文分析內容影響可忽略不計,但多路徑誤差在站星間差分無法削弱,綜上所述,原始觀測序列中僅存在多路徑誤差和噪聲.

原始觀測數據使用goGPS軟件( https://sourceforge.net/projects/gogps/),使用最小二乘方法的單歷元解算基線,基于站心坐標系下得到基線的E、N、U方向分量.

3.2 實驗方案

為了更好展現耦合模型的預測性能,設置如下方案進行對比:

方案一:EMD-LSTM耦合模型;

方案二:EMD方法降噪后直接以LSTM網絡預測實驗.

為了比較建模方法的預測結果,采用平均百分比誤差(MAPE)和均方根誤差(RMSE),兩個指標來衡量模型的預測結果,數值越小,模型精度高,則說明預測效果好.

MAPE計算公式為:

(16)

MAPE值反映的是同組數據的不同網絡訓練出的模型優劣情況,與訓練樣本大小無關,MAPE值僅可評價同組數據在不同模型下的效果,不同訓練數據下的指標大小無法進行評價.

RMSE計算公式為

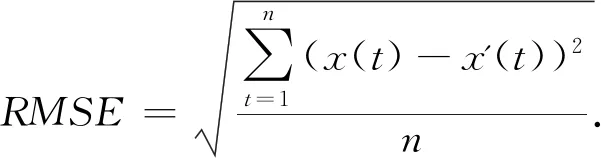
(17)

3.3 BDS實驗結果分析

對當天進行預測時,首先取前一天原始觀測數據為訓練數據,該天數據為測試數據,若對DOY134進行預測時,需取DOY133為訓練數據,其中原始觀測數據如圖2所示. LSTM網絡迭代次數為100次,輸入變量數為100歷元,輸出變量數為1歷元,時間步長設置為256,隱含層為12. 為了減小建模誤差,在進行訓練前將數據進行歸一化處理,預測后進行反歸一化即得真實預測值.

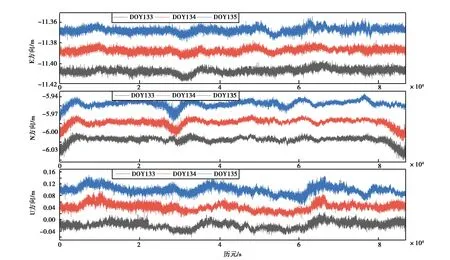
圖2 三天的原始坐標序列

為方便觀測坐標序列趨勢,在DOY134和DOY135各方向添加一定數值. 接收機雖裝有扼流圈天線,由圖2所示,多路徑誤差依然明顯,同時證明了硬件端削弱多路徑誤差程度有限. 限于篇幅,僅以E方向為例. 首先將訓練數據進行EMD多尺度分解,圖3為DOY133的E方向坐標序列經EMD分解的模態分量圖.

圖3 DOY133的E方向坐標序列EMD分解結果

分解得13個模態分量與1個殘余分量,計算分解提取尺度的RP系數在IMF4開始RP大于等于1,IMF1到IMF3均為高頻的隨機噪聲并剔除. 對IMF4至IMF13和Res分別進入LSTM網絡訓練和預測,并對預測得到的分量重構多路徑誤差. 圖4為兩組方案的預測結果.

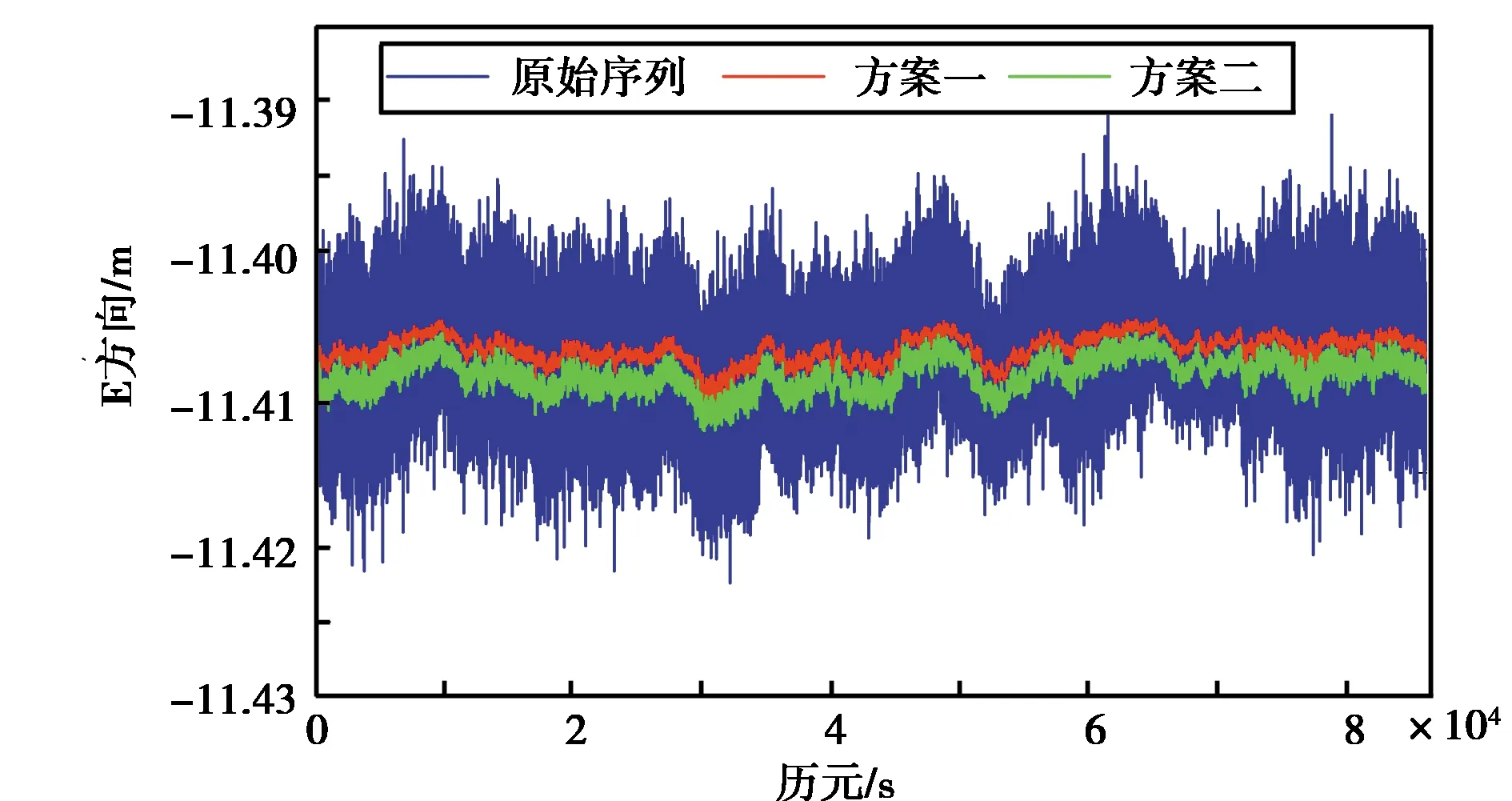
圖4 兩種方案的預測結果

圖5 兩種方案消除多路徑誤差的坐標序列

如圖4～5所示,兩種方案的預測結果雖在趨勢上具有一致性,但二者明顯存在偏移.其中,兩種方案得到的殘差序列,均呈現正態分布,方案二的殘差序列明顯存在滯后性,即并不在0處波動,這也滿足深度學習方法在預測中存在的滯后性特點,但基于EMD-LSTM耦合預測模型較好的解決了這一問題. EMD-LSTM方法能夠將非線性、非平穩性序列良好的學習序列的深層規律. 由表1所示,EMD-LSTM耦合模型的RMSE和MAPE值均比方案二略優,但方案二的均值較大,即后者在改正多路徑誤差時,有用信息被誤處理.

由表2所示,EMD-LSTM耦合方法能夠有效的削弱多路徑誤差,其中對U方向精度改善程度達到了40.30%、41.00%,對E、N方向改善程度分別為24.91%、22.93%和36.84%、39.07%.

表1 兩種方案消除多路徑誤差的坐標序列指標對比

表2 EMD-LSTM耦合模型消除多路徑誤差前后的RMSE對比

4 結 論

在BDS坐標值域中,因星座異構特性,恒星日濾波方法難以適用. 本文引入EMD-LSTM耦合預測模型,對多路徑誤差進行預測建模并改正,得出以下結論:1)本文設置的兩組方案,且均得到較好的結果,但EMD-LSTM耦合方法改善了深度學習方法預測中存在的滯后性問題,提高了多路徑誤差改善程度;2)EMD-LSTM耦合預測模型能有效地削弱多路徑誤差影響,坐標值域中的多路徑誤差改正不再局限于恒星日濾波方法,對E、N、U方向精度改善明顯. 從本文的研究可以看出,基于深度學習方法的多路徑誤差剔除,在測量數據處理中有著廣闊的應用前景,后期需要解決深度學習在實時多路徑誤差剔除中的應用問題.