冪函數變換的GM(1,1)模型在BDS衛星鐘差預報中的應用研究
蔣玉祥
(西寧市測繪院,青海 西寧 810001)
0 引 言
精密單點定位(PPP)是全球衛星導航系統(GNSS)發展史上又一重大技術革命[1],由于其對于衛星精密星歷軌道誤差和鐘差有極高的要求,所以精密星歷中的軌道誤差和鐘差就成為了PPP一個主要的誤差來源[2].根據國際GNSS服務(IGS)提供的15 min或者5 min間隔的精密衛星軌道和鐘差加密得到用戶所需要的精度成為一個很現實的問題.與此同時我國北斗衛星導航系統(BDS)也在迅速發展.根據IGS發布的精密星歷,利用已有的方法對BDS鐘差進行插值以及預報成為一個熱點問題.
隨著BDS的快速發展,針對精密星歷的插值方法也在迅速發展,目前主要的內插方法包括了拉格朗日(Lagrange)插值、牛頓插值、三次樣條插值、三角函數擬合、勒讓德擬合、廣義延拓逼近法等[3-8].而衛星鐘差預報模型目前主要的方法有灰色理論模型[9-11]、時間序列模型[12]、卡爾曼濾波模型[13]、BP神經網絡模型[14-15]、小波變換模型[15-16]、以及各種組合模型[17-22].這些預報模型針對使用情形的不同進行一定程度的改進和組合對鐘差預報具有很好的實際應用價值.
為實現BDS高精度精密定位,根據BDS原子鐘的特點:頻率高、非常敏感、極易受到外界及其本身因素的影響,從而很難掌握其復雜細致的變換規律,而這些特點符合將系統行為特征的信息累加或者累減建立微分方程,并將累計數據還原的灰色模型.而針對普遍使用的傳統GM(1,1)模型對原始數列的光滑度要求高且預測結果誤差較大的問題,對BDS鐘差數據用冪函數進行處理,進而提高了預測精度.本文結合BDS鐘差數據利用MATLAB編程對GM(1,1)模型和冪函數變換的GM(1,1)模型進行驗證,以改進傳統模型的缺點和不足.
1 Lagrange插值法原理
目前,IGS只提供采樣間隔為15 min或者5 min的精密衛星鐘差,根據其變化的規律一般使用低階的Lagrange插值方法即可獲得滿足精度要求的觀測歷元的衛星鐘差.
首先構造n次插值多項式:
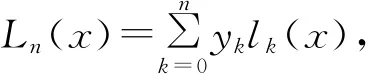
(1)
式中:lk(x)(k=0,1,…,n)都是n次多項式,稱為Lagrange插值基函數.將插值基函數簡化為
P(x0)=y0,P(x1)=y1,…,P(xn)=yn.
(2)
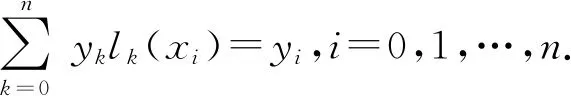
(3)
lk(x)需滿足:
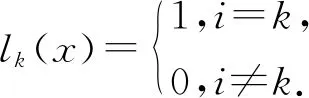
(4)
由此,根據n個節點xi(i≠k)都是n次多項式lk(x)的零點,故有:
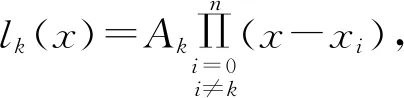
(5)
式中,Ak為待定系數,再由式(4)得到
從而得到最終結果:
(6)
式(6)就是Lagrange多項式插值的基本原理,利用BDS鐘差進行插值時,自變量x為觀測時刻, 因變量y為精密星歷給出的該時刻的鐘差.故想要獲得任意時刻衛星鐘差的n階拉格朗日插值,必須至少有n+1個時刻的衛星鐘差.當插值點位于插值區間的中央時,可以保證最佳的內插效果.
BDS鐘差進行高精度預報時,首先用Lagrange插值根據需要進行插值,其次利用預報模型進行預報,即可得出需要的歷元時刻對應的衛星鐘差.
2 冪函數變換的GM(1,1)模型
針對傳統GM(1,1)模型的缺陷,利用冪函數變換法對模型進行改進,以提高原始數據數列的光滑度,進而降低預報結果的預測誤差.
冪函數變換的GM(1,1)模型的建模過程如下:
首先,設原始數據列為
y(0)(t)={y(0)(1),y(0)(2),…,y(0)(n)}.
(7)
對原始數據做基于冪函數的變換:
x(0)(t)={x(0)(1),x(0)(2),…,x(0)(n)},
(8)
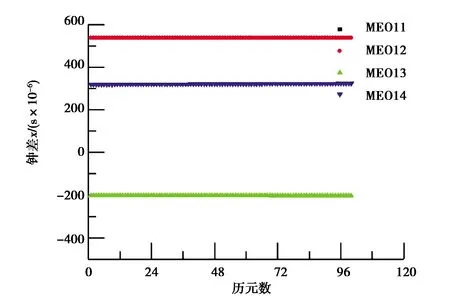
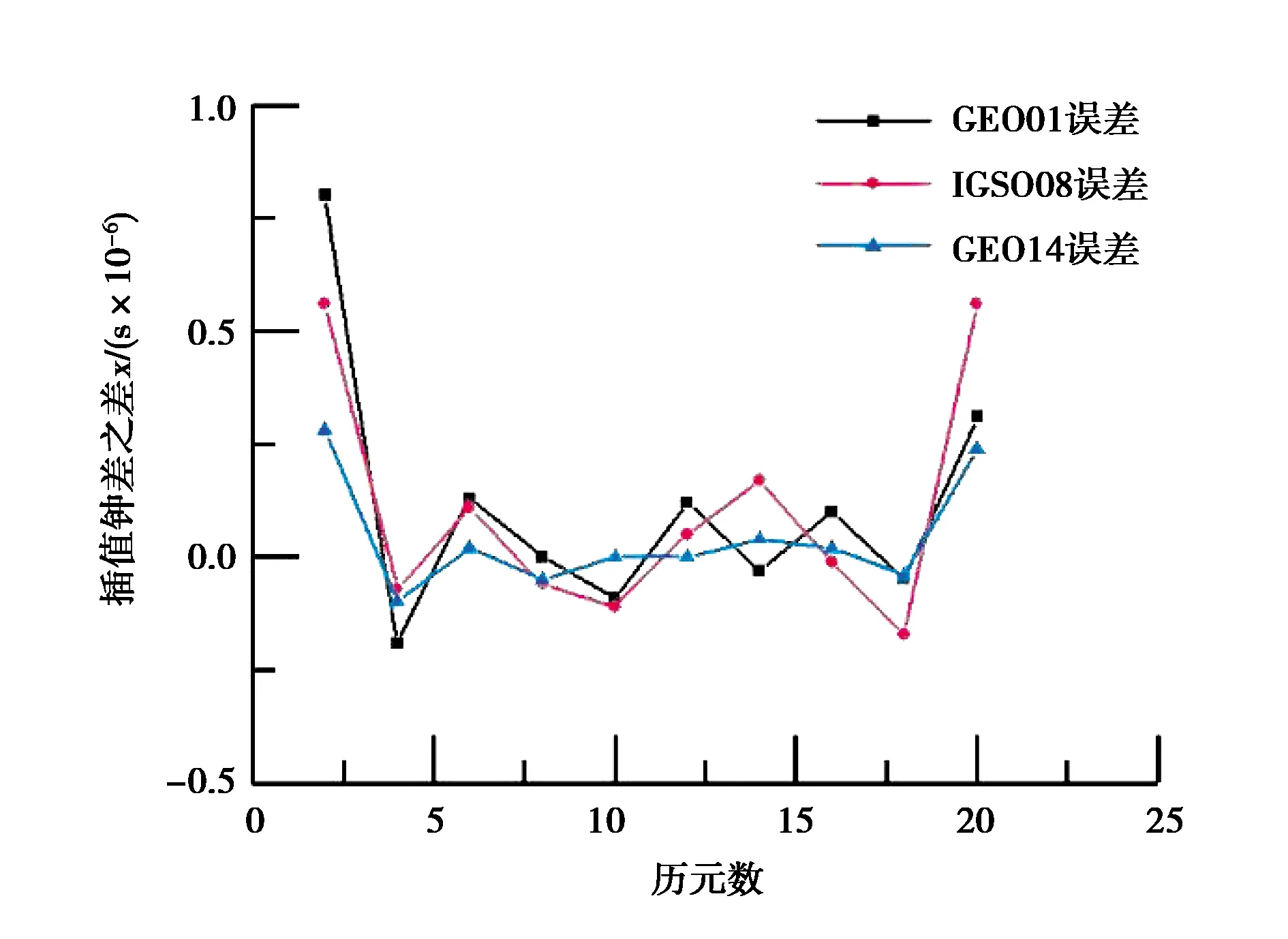
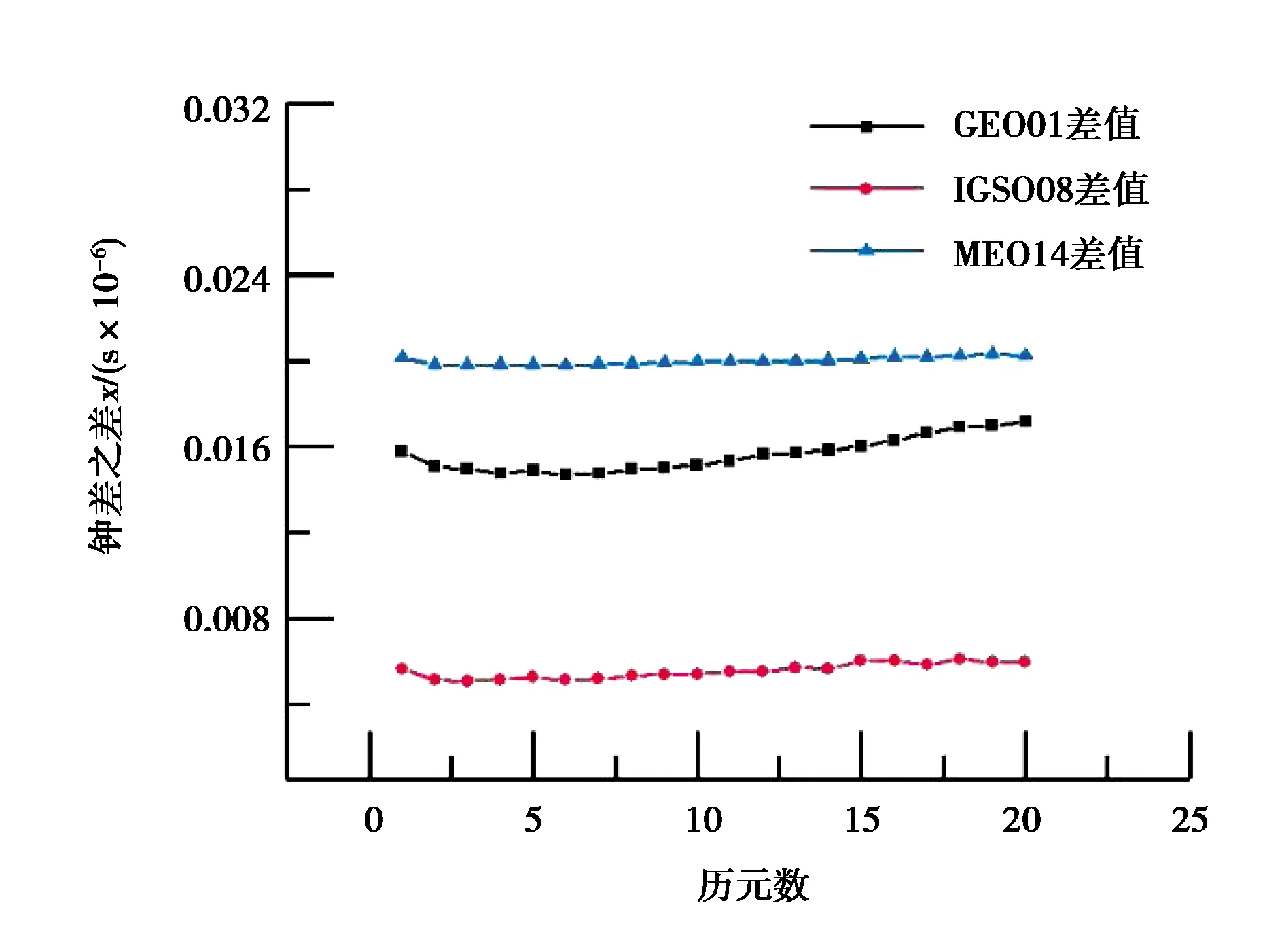
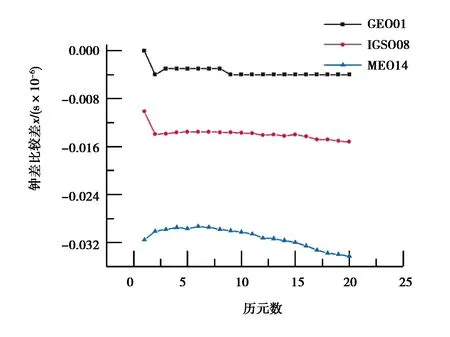
式中,x(0)(t)=[y(0)(t)]-a,t=1,2,…,n,0 其次,對x(0)(t)進行一次累加(1-AGO)生成一次累加序列: x(1)(k)={x(1)(1),x(1)(2),…,x(1)(n)}, (9) (10) (11) yn=[x(0)(2),x(0)(3),…,x(0)(n)]T. (12) 將求得的參數α、u值代入時間響應函數,即可得. (13) 累減還原后得到的預測模型為 (14) 最后,將函數還原后即可得到預測數據: (15) 式中:k表示BDS衛星的某時刻;x表示對應時刻衛星鐘差的冪函數變換;y表示該時刻的衛星鐘差. 式(15)為利用冪函數變換改進的灰色理論模型. 數據選自NASA(National Aeronautics and Space Administration)數據分析中心(ftp://cddis.gsfc.nasa.gov/pub/gps/products/mgex/)發布的多模混合數據中篩選出的2018年7月30日的采樣率為5 min的BDS精密星歷.數據中包含了14顆BDS衛星,其中地球靜止軌道(GEO)衛星5顆(C01-C05)、傾斜地球同步軌道(IGSO)衛星5顆(C06-C10)、中圓地球軌道(MEO)衛星4顆(C11-C14).歷元總數為288,采樣區間為0:0:0到23:55:0.將10 min歷元間隔的偶數歷元衛星鐘差作為將要插值的實際值,將10 min歷元間隔的奇數歷元衛星鐘差作為插值節點,首先采用Lagrange插值,然后利用傳統灰色理論模型和冪函數變換改進的灰色模型進行預報.并且將預報結果與原始觀測值進行對比分析,得出最終的預測結果精度. 圖1~3分別示出了2018年7月30日的BDS衛星GEO、IGSO、MEO三種衛星的偶數歷元鐘差統計.得出GEO衛星可利用1、4、5號衛星進行計算對比,而2、3號衛星鐘差有問題,無法使用;IGSO衛星都可以作為計算對比數據;MEO衛星中12、13、14可以作為計算對比數據,而11號衛星鐘差存在問題,無法使用. 圖1 GEO衛星鐘差統計 圖2 IGSO衛星鐘差統計 圖3 MEO衛星鐘差統計 利用Lagrange插值將BDS星歷中的三種鐘差分別選擇一顆衛星進行插值計算,GEO衛星選擇1號、IGSO衛星選擇8號、MEO衛星選擇14號,并且將0 min,10 min,20 min,…,110 min作為插值節點,選擇10階插值,可以得到5 min,15 min,25 min,…,105 min的插值結果,如圖4所示,插值與實際值保持一致;并且將插值結果與實際值做差可以得到如圖5所示結果,包含端點龍格現象在內的所有插值均滿足小于10-10的結果. 圖4 三種衛星的衛星鐘差插值 圖5 三種衛星的衛星鐘差之差 根據上文的插值結果剔除端點值后,利用傳統灰色理論模型和冪函數變換改進的灰色理論模型分別進行鐘差預報.可以得到GEO01、IGSO08和MEO14衛星的灰色模型鐘差預測值如圖6~8所示.并且得出預測值與實際值的差值,如圖9所示,1號衛星的差值在10-8左右,8號衛星的差值在10-9左右,14號衛星的差值可以達到10-10左右,精度滿足鐘差預測精度. 圖6 GEO衛星灰色理論傳統方法預測值 圖7 IGSO衛星灰色理論傳統方法預測值 圖8 MEO衛星灰色理論傳統方法預測值 圖9 傳統灰色模型預測值與實際值之差 利用冪函數改進的灰色理論模型進行預報可以得到GEO01、IGSO08和MEO14衛星的改進預測結果,如圖10~12所示,可以看出1號衛星鐘差預測值與實際值之差在10-8左右,8號衛星的鐘差預測值與實際值之差在10-9左右,14號衛星鐘差預測值與實際值之差在10-10左右,均滿足預報精度要求;并且得出冪函數變換改進的灰色模型預測值與實際值的差值,如圖13所示,1號衛星的差值在10-8左右,8號衛星的差值在10-9左右,14號衛星的差值可以達到10-10左右,精度滿足鐘差預測精度. 圖10 GEO衛星冪函數變換改進灰色模型預測值 圖11 IGSO衛星冪函數變換改進灰色模型預測值 圖12 MEO衛星冪函數變換改進灰色模型預測值 圖13 冪函數變換改進灰色模型預測值與實際值之差 圖14 改進模型與傳統模型鐘差之差的差值 根據傳統灰色模型的預測值和實際值的差與冪函數改進的灰色模型預測值與實際值的差值之差,由圖14所示可知冪函數改進后的灰色模型相比原模型預測結果更加接近原始數據中的鐘差.以GEO01、IGSO08和MEO14為例,得出當預測值越接近原始觀測值時,則改進模型預測結果越好. 在BDS衛星鐘差插值與預報中,Lagrange插值可以滿足高精度計算要求;而傳統GM(1,1)模型對三種衛星的鐘差值預報結果都可以得到一定的精度,但由于鐘差的不確定性、敏感性,導致有時候鐘差的波動比較大,從而會降低傳統灰色模型的預測精度,限制了其適用范圍.根據冪函數做變換改進灰色模型,則有效提高了原始數據的光滑度,由此建立的灰色模型預測精度也有效提高,冪函數變換的灰色模型在鐘差預報中具有實際使用意義,并且更加可靠和適用.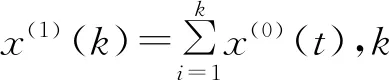
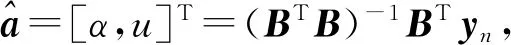
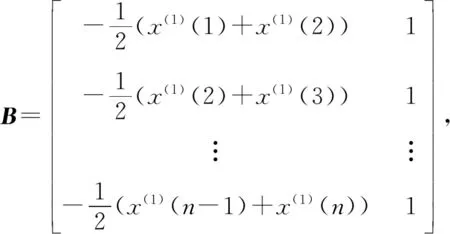


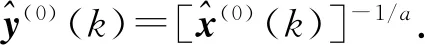
3 BDS精密鐘差預報算例分析
3.1 數據來源以及統計


3.2 BDS精密星歷鐘差插值分析

3.3 BDS精密星歷預報值分析




4 結束語

