民機液壓管路膨脹環結構參數影響分析

郭長虹， 史康俊， 權凌霄， 蔣紅巖2， 崔 超

(1.燕山大學 機械工程學院， 河北 秦皇島 066004； 2.南京機電液壓工程研究中心， 江蘇 南京 211153)

引言

飛機液壓傳動系統可認為是飛機的血管與肌肉，是飛機強健體魄的標識。液壓管路是飛機液壓傳動系統中最多的液壓系統輔件，其安全性與可靠性尤為重要。飛機液壓管路系統在服役過程中工作環境非常復雜，主要承受介質壓力、溫度、機體變形、振動及加速度載荷的交叉耦合作用。民機對可靠性要求特別高，據統計液壓管路失效占其元件故障的52%以上[1]，其失效形式主要有兩類：一是管路靜強度破壞；二是液壓泵壓力脈動、發動機傳動機匣振動和作動器運動等激勵源的頻率與管路系統固有頻率接近，誘發諧振[2]，導致管路出現疲勞裂紋萌生[3-4]。在民機液壓管路系統設計工程中，經常通過在液壓管路上增設一定數量的膨脹環來“容讓”管路內油液壓力、溫度和機體結構變形等載荷引起的形變，從而消弱此形變引起的額外應力集中。管路膨脹環的使用會導致管路空間構型變得復雜、管路系統重量增加，但是更嚴重的是影響液壓管路系統的靜力學特性和動力學特性，從而改變液壓傳動系統的工作性能。研究液壓管路膨脹環關鍵結構參數對管路特性的影響規律具有重大意義，并且為其優化設計奠定一定基礎。

近年來，為了提高液壓管路系統的可靠性，對液壓管路系統約束、管路振動特性和管路布置方案研究較多[5-9]，然而涉及液壓管路結構參數對管路靜力學特性和動力學特性影響的研究較少。歐陽小平等[10]考慮液壓管路曲率和摩擦對彎曲管路固有頻率的影響，結果表明管路曲率影響更加明顯，但是并沒有對管路折彎角度和跨度等其他參數的影響進行研究分析。付永領等[11]應用有限元單元法和計算流體力學法探索了彎管轉角對管路振動特性的影響規律，研究發現當管路彎頭的轉角從90°降低到60°時其振動幅值和振動峰峰值會大幅降低，這表明彎曲管路參數展開研究十分重要。權凌霄等[12]用傳遞矩陣法建立了液壓管路的數學模型，并對其進行應力分析、模態分析和振動響應分析，為液壓管路系統優化設計提供了理論指導。IRIE等[13]利用傳遞矩陣法分析求解了Euler-Bernoulli梁模型，HERRMANN等[14]在研究彎管路振動特性時將90°彎管等分為微小直管路進行振動分析，為用傳遞矩陣法求解管路動態特性奠定了基礎。

本研究通過傳遞矩陣法建立了帶膨脹環的民機液壓管路動力學數學模型，在有限元仿真軟件中求解了液壓管路最大集中應力和一階固有頻率，研究膨脹環關鍵結構參數對其靜力學特性和動力學特性的影響規律。

1 膨脹環模型簡化及關鍵結構參數選取

1.1 膨脹環模型簡化

某民機左側機翼區域的液壓管路膨脹環三維模型如圖1所示，在該管路膨脹環上卡箍布置在直線管段，且滿足一定的管路支承間距要求。將該液壓管路膨脹環進行結構簡化，對每段直線管段和彎曲管段都進行編號，如圖2所示。

1.2 膨脹環關鍵結構參數選取

液壓管路膨脹環的結構參數包括：管路材料屬性、管路外徑D、管路壁厚e、折彎角度σ、彎曲半徑R、跨度S和高度h。下面對各膨脹環參數取值范圍進行分析。

圖1 膨脹環三維模型

圖2 膨脹環結構簡化模型

1) 管路材料屬性、外徑和壁厚

在飛機液壓管路系統設計過程中，考慮許用能量損失、液壓系統設計壓力和管路系統重量等制約，通過流速限制法和壓降限制法確定使用的液壓管路規格(材料、外徑和壁厚)[15]。在之后進行液壓管路系統安裝布置設計時，管路規格不會發生變化，因此其不作為設計變量。本研究選取管路材料為不銹鋼，管路外徑0.375 in，壁厚0.02 in。

2) 折彎角度

在民機液壓管路設計規范中規定，管路折彎角度σ≥90°。本研究選取管路膨脹環折彎角度取值范圍為105°≤σ≤135°。

3) 彎曲半徑

彎曲半徑的確定涉及到彎管模具的設計制造，推薦使用的彎曲半徑不宜過多，不然會影響彎管設備的使用通用性。在民機液壓管路設計規范中，管路彎曲半徑有6個推薦使用值，在所有彎曲半徑中，最優推薦值為4D，最小彎曲半徑為3D，最大彎曲半徑為6D。本研究選取管路膨脹環彎曲半徑取值范圍為2.5D≤R≤6D。

4) 跨度和高度

在民機液壓管路設計規范中，對膨脹環跨度和高度沒有明確規定和要求。本研究選取路跨度取值范圍為8 in≤S≤16 in，高度取值范圍為3 in≤h≤7 in。

2 膨脹環動力學數學模型構建

利用傳遞矩陣法建立液壓管路膨脹環數學模型，通過各直管段、彎管段以及支承位置處的傳遞矩陣的依次乘積運算，得到膨脹環總傳遞矩陣[16]為:

H=H8H7Ht8HJKHt7H6Ht6HHIHt5H5

H4Ht4HEFHt3H3Ht2HCDHt1H2H1

(1)

其中，H1,H2,H3,H4,H5,H6,H7,H8分別為直管段1～8的傳遞矩陣；HCD,HEF,HHI,HJK分別為彎管段CD,EF,HI和JK的傳遞矩陣；Ht1,Ht2,Ht3,Ht4,Ht5,Ht6,Ht7,Ht8分別為各直線段與彎管段之間的連接點的點傳遞矩陣。

求得液壓管路膨脹環總傳遞矩陣H為:

(2)

液壓管路膨脹環最左端到最右端的傳遞關系為:

(3)

即:

(4)

式中，y為截面的撓度;θ為截面轉角;M為彎矩;Q為剪力且均為正值。液壓管路最左端與最右端為固支狀態，邊界條件為:

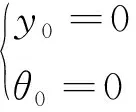
(5)

(6)

將上式(5)代入式(4)，可得:

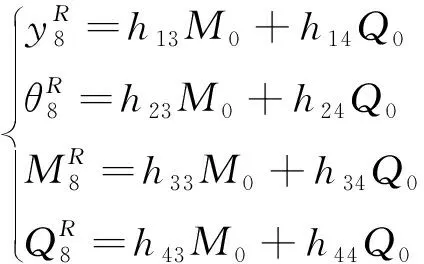
(7)

(8)

當剩余彎矩為0時，得到的結果即為液壓管路膨脹環的各階固有頻率[16]，由于液壓管路膨脹環最左端彎矩M0≠0，所以需滿足:

(9)

將邊界條件式(6)代入式(7)中，可得:

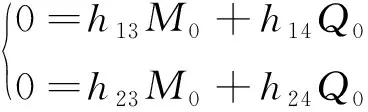
(10)

由式(7)可知，管路左端M0,Q0不全為0，所以:

(11)

由于傳遞矩陣的元素hij是固有頻率ω的函數，式(11)即為管路的固有頻率方程，該方程的根即為系統的固有頻率。在MATLAB中進行編程求解該固有頻率，過程如圖3所示。

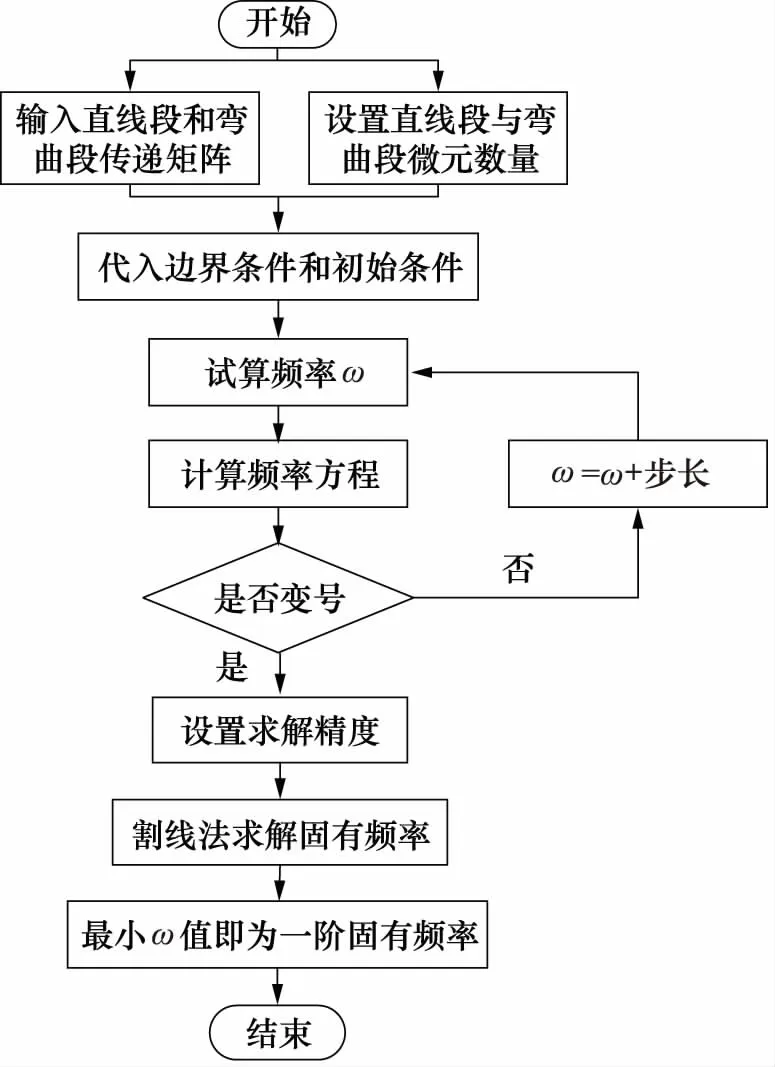
圖3 傳遞矩陣法編程求解過程

3 膨脹環結構參數影響仿真分析

在ABAQUS有限元仿真分析過程中，采用控制變量法研究靜力學特性和動力學特性隨某一關鍵結構參數的變化規律。選取的管路材料為不銹鋼，管路外徑0.375 in，壁厚0.02 in。在全部管路靜力學仿真載荷參數設置過程中，管路均只承受分布均勻的21 MPa壓力載荷和21℃溫度載荷。由于溫度載荷為室溫，所以膨脹環產生的額外應力主要是由于管內壓力載荷引起。

3.1 膨脹環折彎角度影響分析

建立除折彎角度不同其他結構參數均相同的7根液壓管路膨脹環模型，管路折彎角度從105°變化到135°，每間隔5°建立1根液壓管路模型。

1) 折彎角度對靜力學特性影響分析

鑒于文章篇幅，僅給出折彎角度為105°和135°時液壓管路膨脹環靜力學分析應力云圖結果，分別如圖4所示。

最后通過有限元靜力分析結果可得，當折彎角度改變時，膨脹環最大應力位于第1個和第4個折彎處。

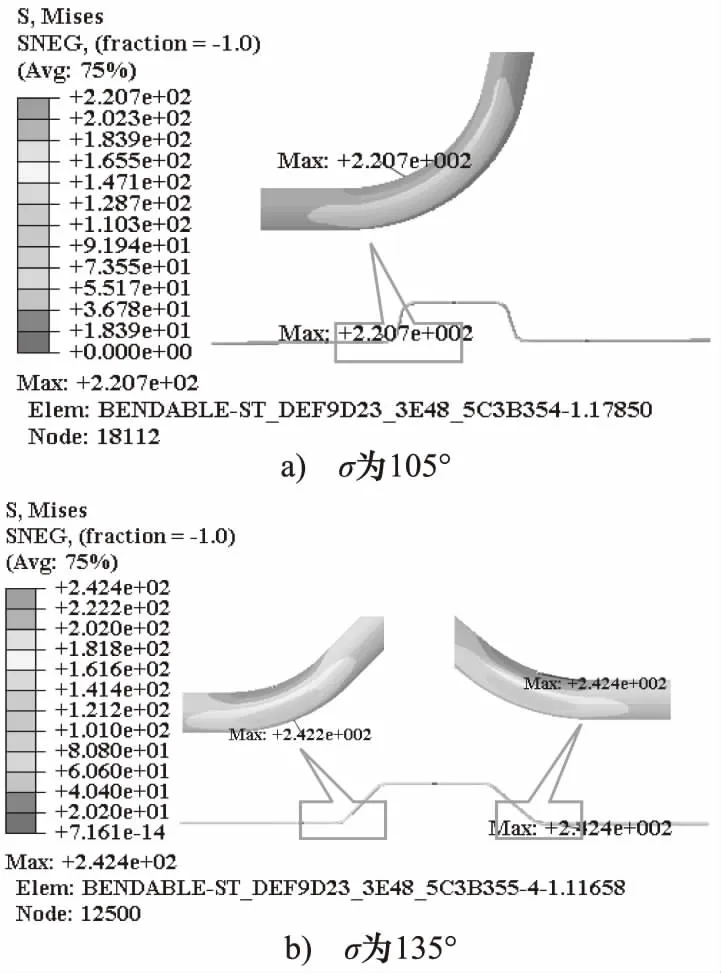
圖4 折彎角度改變時靜力分析應力云圖

因為本研究的管路膨脹環是關于垂直中軸對稱，并且壓力載荷和溫度載荷都均勻分布，所以第1個折彎和第4個折彎處的應力分布情況相同。因此后文只給出1處對稱結構位置的應力放大云圖。液壓管路膨脹環最大應力pmax隨折彎角度σ的變化規律擬合結果如圖5所示。

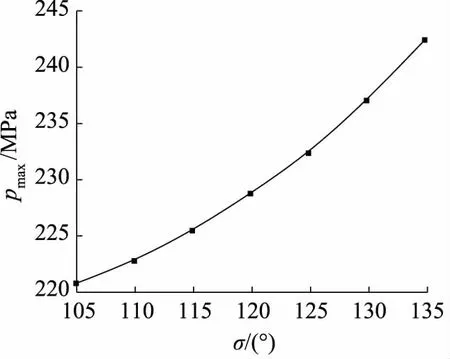
圖5 最大應力隨折彎角度變化規律

通過上圖可得，當折彎角度為105°時膨脹環最大應力最小，當折彎角度為135°時膨脹環最大應力最大。膨脹環最大應力隨著折彎角度的增大而逐漸增大，且增大速度逐漸變大。

2) 折彎角度對動力學特性影響分析

通過仿真分析獲得管路膨脹環一階固有頻率f，其隨折彎角度σ的變化規律擬合結果，如圖6所示。

通過圖6可得，當折彎角度為105°時膨脹環固有頻率最小，當折彎角度為135°時膨脹環固有頻率最大。膨脹環一階固有頻率隨折彎角度的增大而逐漸升高，而且升高速率逐漸增快。

圖6 一階固有頻率隨折彎角度變化規律

3.2 膨脹環彎曲半徑影響分析

建立除彎曲半徑不同其他結構參數均相同的6根液壓管路膨脹環模型，管路彎曲半徑取值為2.5D， 3D， 3.5D， 4D， 5D和6D，此時D取值為0.375 in。

1) 彎曲半徑對靜力學特性影響分析

鑒于文章篇幅，僅給出彎曲半徑為2.5D和6D時液壓管路膨脹環靜力學分析應力云圖結果，分別如圖7所示。

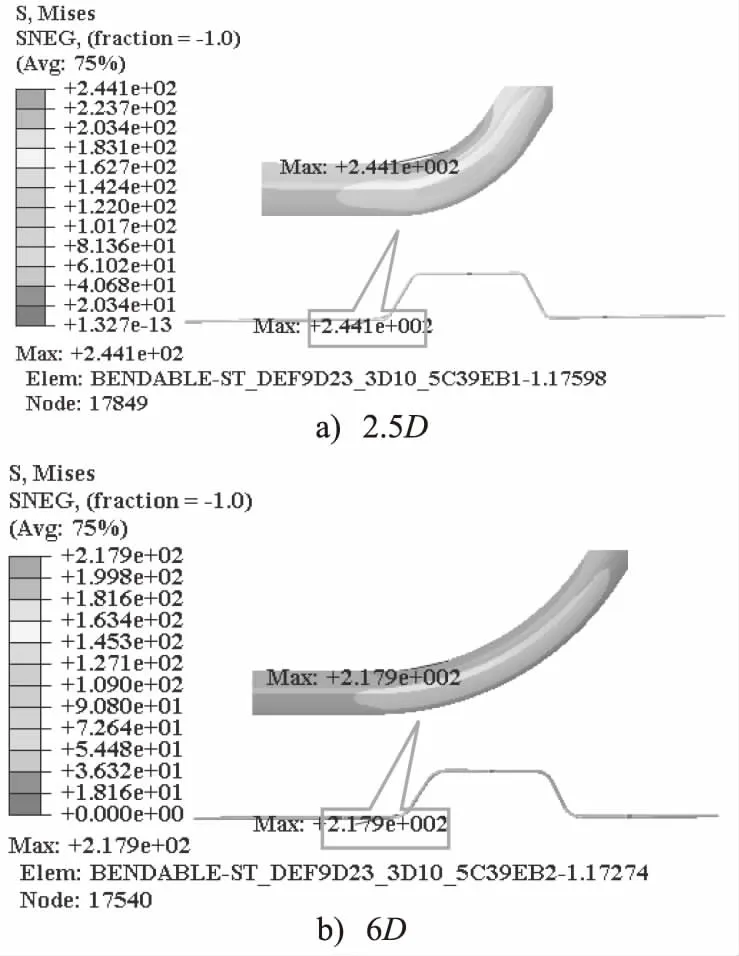
圖7 彎曲半徑改變時靜力分析應力云圖

最后通過有限元靜力分析結果可得，當彎曲半徑改變時，膨脹環最大應力均位于第1個折彎和第4個折彎處。液壓管路膨脹環最大應力pmax隨彎曲半徑R的變化規律擬合結果如圖8所示。

通過上圖可得，當彎曲半徑為2.5D時膨脹環最大應力最大，當彎曲半徑為6D時膨脹環最大應力最小。膨脹環最大應力隨著彎曲半徑的增大而逐漸減小，且減小規律逐漸趨緩。

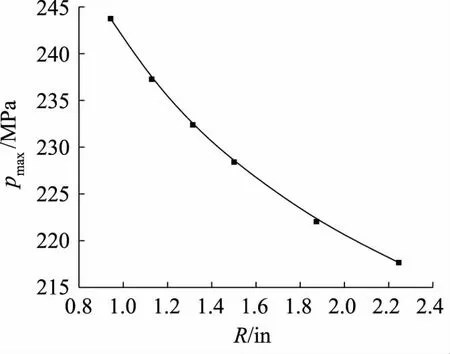
圖8 最大應力隨彎曲半徑變化規律

2) 彎曲半徑對動力學特性影響分析

通過仿真分析獲得管路膨脹環一階固有頻率f，其隨彎曲半徑R的變化規律擬合結果，如圖9所示。

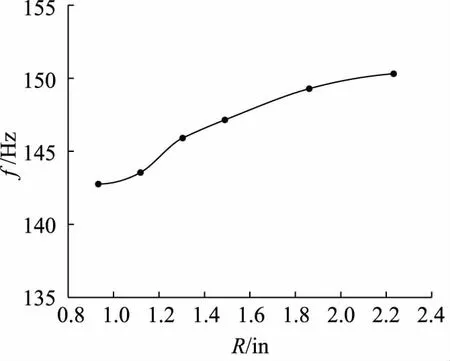
圖9 一階固有頻率隨彎曲半徑變化規律

通過上圖可得，當彎曲半徑為2.5D時膨脹環固有頻率最小，當彎曲半徑為6D時膨脹環固有頻率最大。液壓管路膨脹環一階固有頻率隨彎曲半徑的增大而逐漸升高，而且升高速率逐漸減慢。

3.3 膨脹環跨度影響分析

建立除跨度不同其他結構參數均相同的5根液壓管路膨脹環模型，管路跨度從8 in變化到16 in，每間隔2 in建立1根液壓管路模型。

1) 跨度對靜力學特性影響分析

鑒于文章篇幅，僅給出跨度為8 in和16 in時液壓管路膨脹環靜力學分析應力云圖結果，分別如圖10所示。

最后通過有限元靜力分析結果可得，當跨度改變時，膨脹環最大應力均位于第1個折彎和第4個折彎處。液壓管路膨脹環最大應力pmax隨跨度S的變化規律擬合結果，如圖11所示。

通過圖11可得，當跨度為8 in時膨脹環最大應力最小，當跨度為16 in時膨脹環最大應力最大。膨脹環最大應力隨著跨度的增大而逐漸增大，且增大速度逐漸變大。

圖10 跨度改變時靜力分析應力云圖

圖11 最大應力隨跨度變化規律

2) 跨度對動力學特性影響分析

通過仿真分析獲得管路膨脹環一階固有頻率f，其隨跨度S的變化規律擬合結果如圖12所示。

圖12 一階固有頻率隨跨度變化規律

通過上圖可得，當跨度為10.7 in時膨脹環固有頻率最小，當跨度為16 in時膨脹環固有頻率最大。液壓管路膨脹環一階固有頻率隨跨度的增加先降低再升高。

3.4 膨脹環高度影響分析

建立除高度不同其他結構參數均相同的5根液壓管路膨脹環模型，管路高度從3 in變化到7 in，每間隔1 in建立1根管路模型。

1) 高度對靜力學特性影響分析

鑒于文章篇幅，僅給出高度為3 in和7 in時液壓管路膨脹環靜力學分析應力云圖結果，分別如圖13所示。

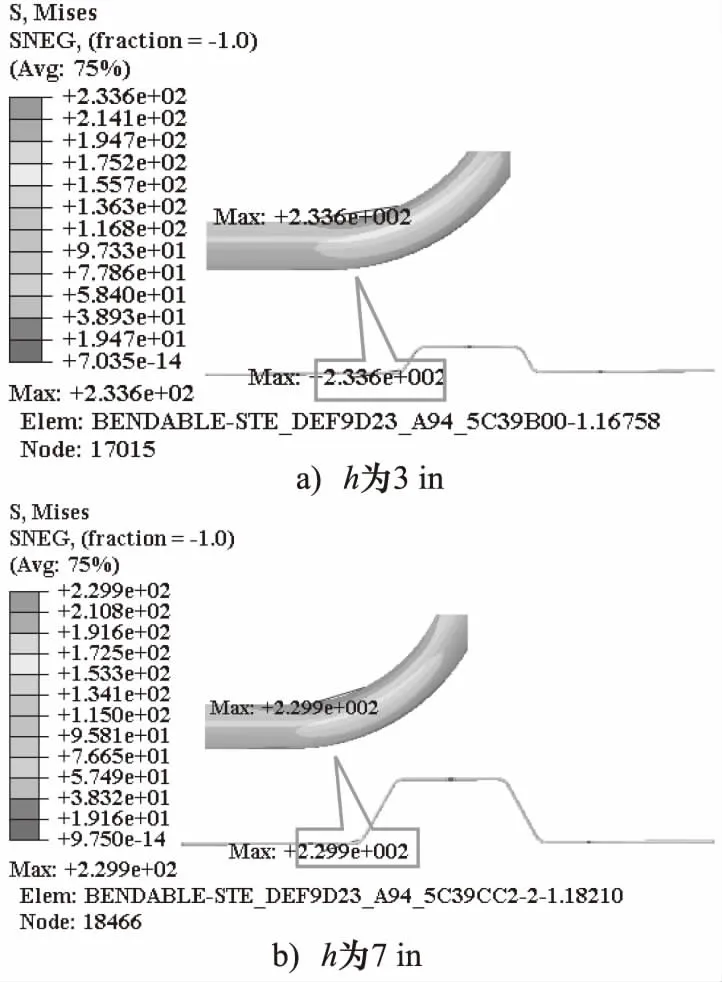
圖13 高度改變時靜力分析應力云圖

最后通過有限元靜力分析結果可得，當高度改變時，膨脹環最大應力均位于第1個和第4個折彎處。液壓管路膨脹環最大應力pmax隨高度h的變化規律擬合結果，如圖14所示。

圖14 最大應力隨高度變化規律

通過上圖可得，當高度為5.2 in時膨脹環最大應力最小，當高度為3 in時膨脹環最大應力最大。膨脹環最大應力隨著高度的增大而先減小再增大。

2) 高度對動力學特性影響分析

通過仿真分析獲得管路膨脹環的一階固有頻率f，其隨高度h的變化規律擬合結果如圖15所示。

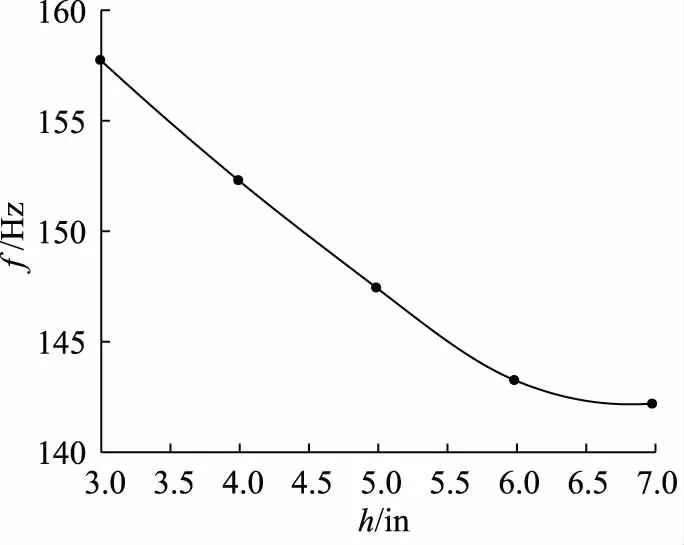
圖15 一階固有頻率隨高度變化規律

通過上圖可得，當高度為3 in時膨脹環固有頻率最大，當高度為7 in時膨脹環固有頻率最小。液壓管路膨脹環一階固有頻率隨高度的增加而降低。

4 驗證分析

4.1 靜力學仿真分析方法驗證

1) 實驗過程

為驗證本研究中使用的靜力學仿真分析方法的正確性，選取某型號飛機前機身區域的一段管徑為0.5 in和壁厚為0.035 in的鋁合金回油管路開展仿真靜力分析和管路靜力學實驗研究，支撐位置、數量與實際使用情況完全一致，該管路三維模型如圖16所示。

圖16 實驗管路模型

實驗管路上一共黏貼了3個自帶溫度補償的三軸應變花，黏貼位置如圖17所示。

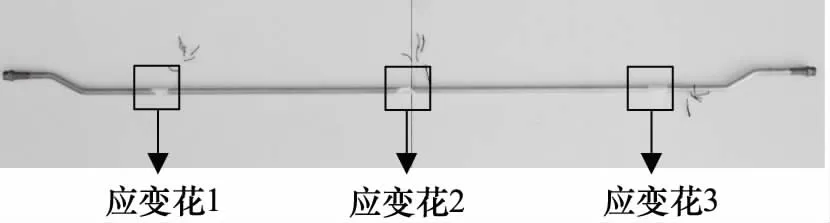
圖17 實驗管路應力測點

進行管路實驗時，工作介質選用10號航空液壓油，管路內壓力達到10 MPa，保持管內壓力穩定，調節溫控箱使管路工作溫度穩定在21℃，管路安裝如圖18所示。

圖18 管路安裝示意圖

2) 實驗結果

對各應力測量點的應力p進行記錄，各應變花的數據如圖19所示，穩定后最大平均應力值即為測量處管路承受的集中應力。

圖19 實驗管路各點應力曲線

3) 仿真結果

通過文中的靜力學分析方法對實驗管路進行仿真靜力學分析，應力云圖如圖20所示。

圖20 實驗管路靜力學分析云圖

在靜力學仿真結果中讀取與實驗管路上張貼應變花相同位置處的應力數值，然后與實驗測得應力數據進行對比，如表1所示。

從表1中可知，實驗與仿真誤差不超過5%，實驗測試結果與仿真分析結果具有較好的一致性。因此，通過實驗測試與仿真分析結果的對比，證明靜力學仿真分析方法正確，可以對分析管路實際工作過程中的應力和應變狀態提供指導和參考依據。

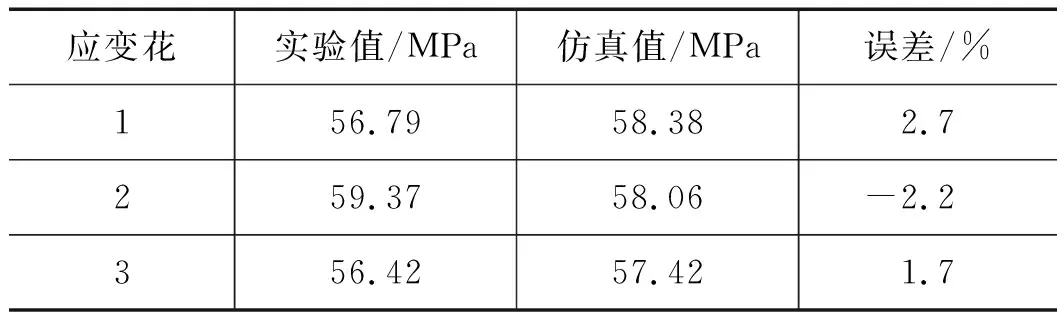
表1 應力實驗與仿真對比

4.2 動力學數學模型驗證

上文中基于有限元仿真軟件探索了膨脹環關鍵結構參數對液壓管路動態特性的影響規律，此時通過MATLAB對液壓管路膨脹環動力學數學模型進行求解分析，得到了膨脹環在不同折彎角度、彎曲半徑、跨度和高度下的一階固有頻率。鑒于文章篇幅，故只給出膨脹環在不同折彎角度下的一階固有頻率，并將其與仿真分析得到的一階固有頻率進行對比，如表2所示。

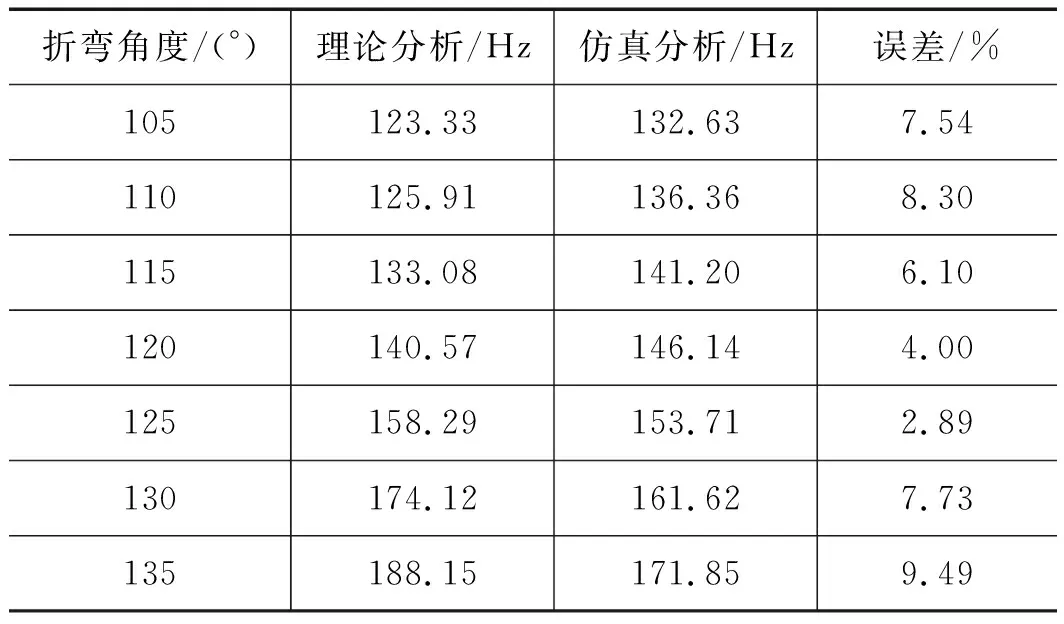
表2 一階固有頻率理論與仿真對比

通過上表可知，理論分析與仿真分析的誤差均小于10%，理論數學模型與仿真模型具有較高的一致性，建立的動力學數學模型準確度較高。

5 結論

研究了液壓管路膨脹環關鍵結構參數對其靜力學特性和動力學特性的影響規律，得出了以下結論。

(1) 液壓管路膨脹環靜力學仿真分析結果與實驗結果誤差低于5%，驗證了靜力學仿真方法的準確性，通過該方法能夠在一定程度上實現對液壓管路靜應力預測，減少實測時間和成本；

(2) 利用傳遞矩陣法建立了液壓管路膨脹環動力學數學模型，通過MATLAB求解了膨脹環在不同結構參數下的一階固有頻率，并將其與仿真結果進行對比，誤差控制在10%以下，證明了動力學數學模型的正確性；

(3) 當進行液壓管路膨脹環設計時，如果對管路靜力學特性要求較高，應該盡量減小膨脹環折彎角度和跨度，增加其彎曲半徑，高度取值在5.2 in左右；如果需要得到一階固有頻率較高的液壓管路，應該盡量增加膨脹環折彎角度、彎曲半徑和跨度，減小其高度。