基于一般集對評價法的節水灌溉方案優選

張 虎 陳 杰

（1.安徽省·水利部淮河水利委員會水利科學研究院 水利水資源安徽省重點實驗室 蚌埠233000 2.安徽省地球物理地球化學勘查技術院 合肥 230022）

節水灌溉方案優選就是從多種給定的工程方案中，經過系統地分析與評價，從而做出決策，選擇最佳方案。方案優選主要考慮項目的技術、經濟、生態和社會等幾個方面，如灌溉水利用率、投資回收期、作物適應性、項目受歡迎程度等相關指標，然而這些評價指標既有正向的影響，也有負向的影響，還有不確定性的影響。評價指標的模糊性、不確定性以及人為因素的主觀性，給方案優選工作帶來了一定的難度[1～2]。為此，本文利用一般集對評價法（general set pair analysis assessment method，GSPAAM）對節水灌溉方案優選方法進行了實例研究與應用。

1 一般集對評價法模型

1.1 模型原理

首先，根據具體問題，將集合A 和集合B 組成集對H=(A，B)。然后，對集對H 的特性展開分析[3～5]。

假設集對H 的特性總數為n，其中S 為同一性的個數，P 為對立性的個數，F= n-S-P 為兩個集合既不對立又不同一的個數（F 為差異性個數），所以，得出兩個集合的聯系數表達式為：

式中：a、b、c 為集對的聯系度分量，并且滿足a+b+c=1 的歸一化條件。

式（2）從不同角度定量解釋了確定性與不確定性。a、c 是相對確定的，b 是相對不確定的。

1.2 模型計算步驟

模型計算步驟如下[5]：

步驟1：將各等級標準進行符號量化處理。對于1 級標準，記為集合B1=（1，1，…，1）；對于2級標準，記為集合B2=（2，2，…，2）；依此類推，對于K 級標準，記為集合BK=（K，K，…，K）。

步驟2：將評價對象A 進行符號量化處理。評價對象A 的各指標值與對應指標各級的標準值進行比較，如落入第1 級，該指標為第1 級，將該指標量化為符號“1”；如落入第k 級，將該指標量化為符號“k”。逐個指標依次比較，得到符號量化的集合A，比如A1=（1，3，…，3）。

步驟3：構造集對H=（A，Bk）。將A 與Bk相對應的元素一一進行對照，統計符號相同的個數，記為S；統計符號相差1 級的個數，比如2 與1、2與3，記為F1；統計符號相差2 級的個數，比如2 與4、1 與3，記為F2；依此類推，統計相差K-2 級的個數，比如2 與K，記為FK-2；統計相差K-1 級的個數，比如1 與K，記為P。得到K 元聯系度：

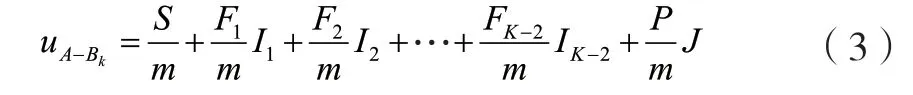
式中：S+F1+F2+…+FK-2+P＝m。

步驟4：確定差異不確定分量系數I1，I2，…，IK-2的值。差異不確定分量系數可以采用經驗取值法或均勻取值法來確定。

步驟5：將I1，I2，…，IK-2和J 代入上式中得到綜合評價指標值——聯系數，即kBAu?′（k=1，2，…，K）。根據聯系數的大小判斷A 所屬的評價等級，聯系數最大者對應的等級就是A 的評價，即根據kBAu?′推斷A 為第k 級。 如 3BAu?′最大，則推斷A 為第3 級。

2 案例應用

本文基于一般集對評價法模型，對某節水灌溉項目的管道灌溉、噴灌、滴灌和小管出流灌溉等4個待選方案的11 個技術經濟評價指標進行綜合評價與分析，選出最佳方案，作為項目決策的重要依據[6～9]。各待選方案評價指標見表1。

建立各方案的評價指標體系：凈現值x1（萬元），收益率x2（%），投資回收期x3（a），效益費用比x4，灌水均勻度x5（%），灌水強度x6（mm·h-1），灌水利用率x7（%），安全可靠性x8（%），作物適應性x9（%），農民歡迎程度x10（%），便于施工程度x11（%）。各方案的均值與均方差見表2。

根據本案例，應先確定各等級標準。根據均值標準差法將各指標分為三個級別：好（1 級）、中（2級）、差（3 級）。具體劃分為：對于越大越優的指標，1 級、2 級、3 級分別對應區間[x+k2s，+∞)、[x+k1s，x+k2s)、(0，x+k1s)，其中，x、s 分別為各方案技術經濟評價指標值的均值和均方差，經驗系數k1=-0.5，k2=0.5；對于越小越優的指標，1 級、2 級、3 級分別對應區間(0，x+k1s)、[x+k1s，x+k2s)、[x+k2s，+∞)，k1、k2同上。評價等級標準見表3。

把各方案確定為集合Ai(i=1，2，3，4)。方案1（A1），方案2（A2），方案3（A3），方案4（A4）。然后根據表3，將集合Ai(i=1，2，3，4)進行符號量化處理，計算結果見表4。最優等級標準為集合B1(1，1，1，1)，將集合Ai(i=1，2，3，4)與B1(1，1，1，1)構建為集對H=(Ai，B1)(i=1，2，3，4)。統計集對H 符號相同的個數，符號相差一級的個數和符號相差二級的個數，最后計算各集對的聯系數。

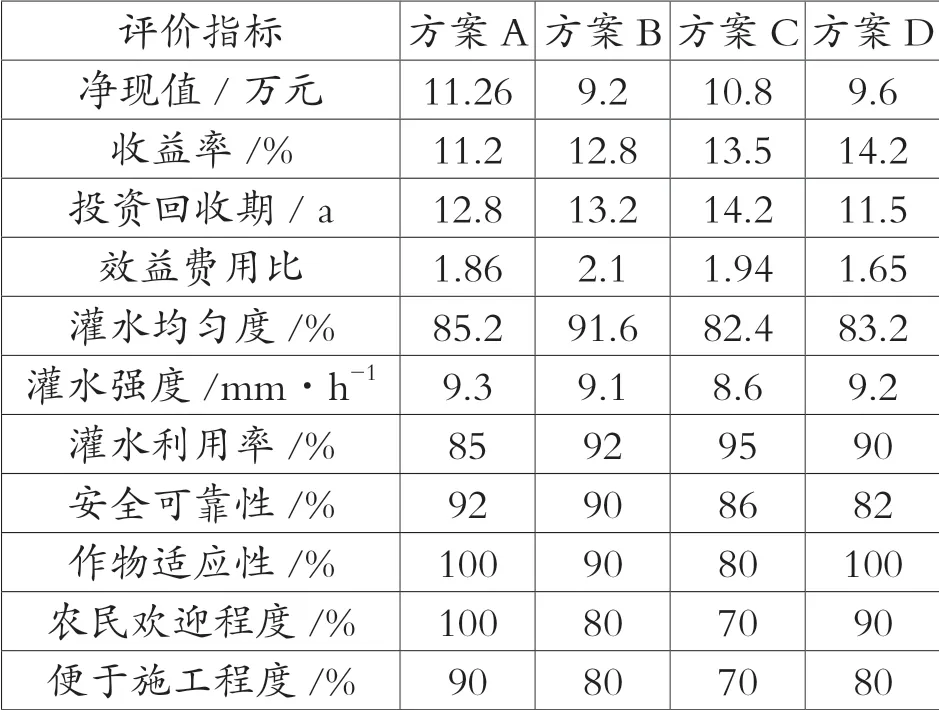
表1 各方案的主要技術經濟指標表

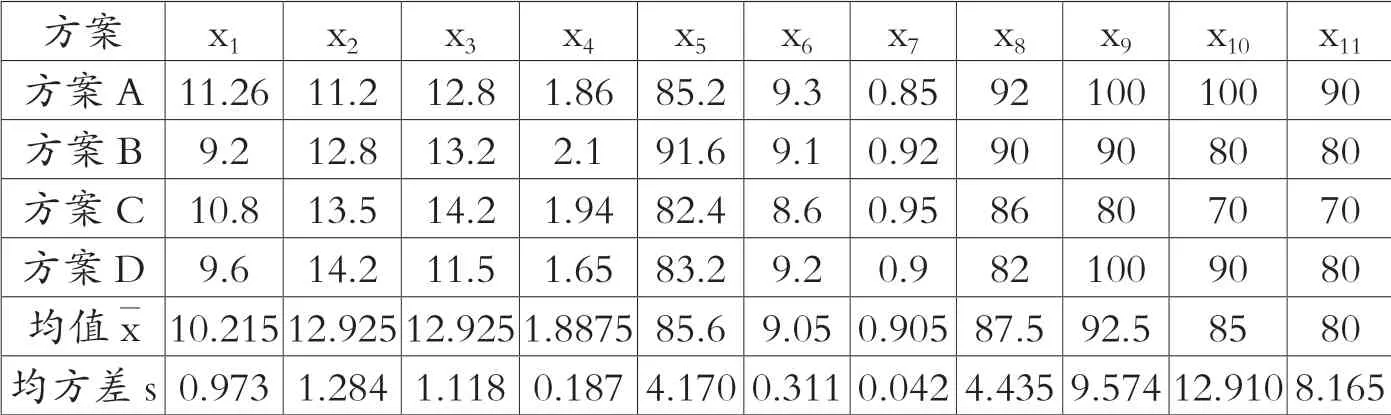
表2 節水灌溉方案指標值及相關統計值表

表3 評價等級標準表

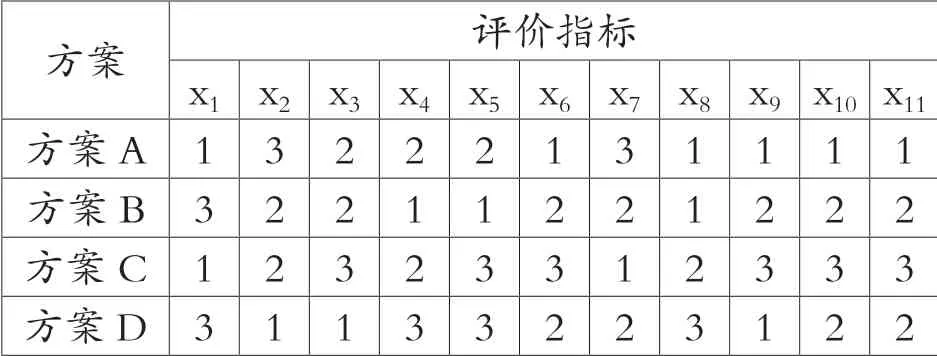
表4 各方案符號量化表

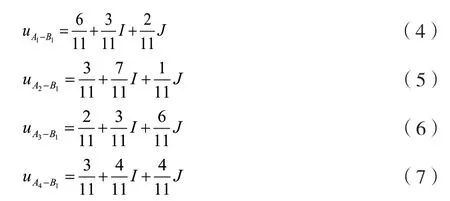
均勻取值法取I=0，J= -1，則各集對的聯系數分別為：

得出，方案A最優，其次是方案B，再次是方案D，最差的是方案C。

經驗取值法取I=0.5，J= -1，則各集對的聯系數分別為：

得出，方案A 和方案B 最優，其次是方案D，最差的是方案C。

從各方案評價指標體系來看，方案A 的11 項指標中有6 項指標為好，3 項指標為中，2 項指標為差，而方案B 的11 項指標中3 項指標為好，7 項指標為中，1 項指標為差。相比較而言，方案A 半數以上指標都為好，故推斷方案A 優于方案B。

所以，該案例所有方案優選排序為：方案A ＞方案B ＞方案D ＞方案C。

3 結語

（1）節水灌溉方案優選涉及到多個指標和因素，是一個比較復雜的系統評價問題。本文通過建立一般集對評價模型，在處理各種不確定問題上，把眾多評價指標變換成單一綜合評價指標，從而簡化了思路，易于計算與操作，為含有多個指標的節水灌溉方案優選問題提供了一種較為可靠的決策依據。

（2）評價結果說明了差異不確定系數分量取值過程有人為主觀因素的干擾，直接影響了最終的評價結果。因此，在方案優選決策中盡量降低人為因素的影響，減小決策者的偏好，對方案最后的優先結果有著重要意義。

（3）一般集對評價法理論的不足之處是沒有充分考慮評價指標的等級邊界的模糊性以及各評價指標的權重，在今后的研究中，考慮這方面的內容會使評價結果更加穩定與合理。