高超聲速滑翔飛行器傾側(cè)角影響分析

孟繁卿，田康生

(1. 空軍預(yù)警學(xué)院研究生大隊(duì)， 武漢 430019； 2. 空軍預(yù)警學(xué)院四系， 武漢 430019)

0 引 言

隨著各國(guó)反導(dǎo)預(yù)警體系的構(gòu)建與完善，傳統(tǒng)彈道導(dǎo)彈的威脅有下降的趨勢(shì)。臨近空間高超聲速飛行器的出現(xiàn)，使得針對(duì)彈道導(dǎo)彈構(gòu)建的反導(dǎo)體系面臨新的挑戰(zhàn)[1]。臨近空間高超聲速飛行器，既具有彈道導(dǎo)彈高速、遠(yuǎn)距離打擊的特點(diǎn)，又具有航空飛行器可靈活機(jī)動(dòng)的特點(diǎn)。臨近空間高超聲速飛行器的獨(dú)特優(yōu)勢(shì)使其逐漸成為各國(guó)研究的熱點(diǎn)。

臨近空間高超聲速滑翔飛行器作為當(dāng)前高超聲速飛行器研究的重點(diǎn)，在飛行過程中依靠空氣動(dòng)力實(shí)現(xiàn)滑翔飛行，其飛行速度大于Ma5，飛行高度大于20 km。高超聲速滑翔飛行器滑翔段的飛行控制參數(shù)主要是攻角和傾側(cè)角[2]，所以飛行器滑翔段的彈道特性也主要受攻角和傾側(cè)角影響。文獻(xiàn)[3]在縱向平面內(nèi)分析了平衡滑翔條件下，飛行器狀態(tài)變量與狀態(tài)變量、狀態(tài)變量與過程變量之間的關(guān)系，分析了跳躍滑翔條件下，初始狀態(tài)對(duì)彈道特性的影響。文獻(xiàn)[4]利用平衡滑翔條件，構(gòu)建了高超聲速飛行器航程與飛行時(shí)間的解析式，定量分析了升阻比對(duì)滑翔射程的影響規(guī)律。文獻(xiàn)[5]在最大升阻比平衡滑翔條件下，利用數(shù)值積分的方法求得了飛行速度、航程等狀態(tài)變量的解析式，提出并證明了最大升阻比平衡滑翔是航程最優(yōu)的彈道的觀點(diǎn)。文獻(xiàn)[6]從工程應(yīng)用的角度分析了再入攻角優(yōu)化問題的多種約束，得到了再入攻角的上下限及攻角設(shè)計(jì)空間，提出了再入攻角剖面的設(shè)計(jì)方案，所提方案在覆蓋區(qū)優(yōu)化問題上有較高的應(yīng)用價(jià)值。文獻(xiàn)[7]將熱流密度、動(dòng)壓和過載等過程約束轉(zhuǎn)化為攻角約束，將過程約束邊界轉(zhuǎn)化為攻角的上下限，減少了彈道規(guī)劃中約束變量的個(gè)數(shù)，降低了彈道規(guī)劃的復(fù)雜度和計(jì)算量。文獻(xiàn)[8]針對(duì)高超聲速飛行器受空氣擾動(dòng)后攻角易發(fā)生變化的問題，分析了攻角動(dòng)態(tài)變化時(shí)對(duì)高超聲速飛行器氣動(dòng)特性的影響，指出其性能參數(shù)的變化規(guī)律雖然沒有顯著改變，但存在遲滯現(xiàn)象。文獻(xiàn)[9]對(duì)高超聲速飛行器在大攻角情況下的氣動(dòng)特性進(jìn)行了分析，指出大攻角時(shí)飛行器的氣動(dòng)參數(shù)呈現(xiàn)非線性的特點(diǎn)，飛行器的縱向靜不穩(wěn)定性隨攻角增大而增大。文獻(xiàn)[10]通過對(duì)高超聲速飛行器的軌跡仿真得到了飛行器升阻比的變化規(guī)律，給出了升阻比的解析表達(dá)式，由升阻比解析式可知升阻比本質(zhì)還是受飛行器攻角控制。

以上文獻(xiàn)的研究成果豐富，為我們明晰高超聲速飛行器的彈道特性、進(jìn)行軌跡規(guī)劃和優(yōu)化提供了很好的借鑒。但不管是彈道特性分析還是彈道規(guī)劃設(shè)計(jì)，多是集中在縱向平面，以攻角的設(shè)計(jì)、優(yōu)化或攻角對(duì)飛行狀態(tài)和過程約束的影響分析為主，而忽略了傾側(cè)角對(duì)飛行器飛行速度、飛行高度和過程約束的影響[2]。為了將已有文獻(xiàn)研究成果的適用范圍進(jìn)一步擴(kuò)展，需要研究?jī)A側(cè)角對(duì)飛行器飛行速度、飛行高度和過程約束的影響。通過分析傾側(cè)角對(duì)高超聲速滑翔飛行器滑翔段飛行速度、飛行高度、過程約束的影響，可為彈道特性分析、彈道設(shè)計(jì)、彈道優(yōu)化和軌跡預(yù)測(cè)等提供借鑒。

1 高超聲速滑翔飛行器滑翔段運(yùn)動(dòng)方程

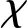
(1)

其中升力、阻力的計(jì)算可由式(2)求得。ρ是空氣密度，S是飛行器的參考面積，CL是飛行器的升力系數(shù)，CD是飛行器的阻力系數(shù)[4,12]。

(2)

(3)

2 飛行彈道控制參數(shù)模型及飛行約束條件

2.1 飛行彈道及彈道控制參數(shù)模型

臨近空間高超聲速滑翔飛行器的典型彈道按照運(yùn)動(dòng)平面可分為：縱向平衡滑翔彈道、縱向跳躍滑翔彈道、橫向無機(jī)動(dòng)彈道、橫向弱機(jī)動(dòng)彈道、橫向強(qiáng)機(jī)動(dòng)彈道。

(4)

縱向跳躍滑翔彈道控制參數(shù)模型即攻角α的參數(shù)模型[13]，如式(5)所示。αmax為最大飛行攻角，α(L/D)max為最大升阻比攻角。V1和V2分別為攻角參數(shù)變化的兩個(gè)臨界速度。

α(V)=

(5)

臨近空間高超聲速滑翔飛行器橫向機(jī)動(dòng)的主要控制參數(shù)是傾側(cè)角ε，如果橫向無機(jī)動(dòng)，則可令傾側(cè)角為零，即ε=0°。

橫向弱機(jī)動(dòng)彈道軌跡平滑，傾側(cè)角通常只翻轉(zhuǎn)一次，飛行器橫向只機(jī)動(dòng)一次。橫向弱機(jī)動(dòng)彈道控制參數(shù)模型如式(6)所示。εd為初始傾側(cè)角。A是飛行器飛行過程中在水平面上的投影點(diǎn)，O是飛行器初始位置在水平面上的投影點(diǎn)，F(xiàn)是目標(biāo)點(diǎn)在水平面上的投影點(diǎn)，B是O和F連線上的一個(gè)參照點(diǎn)。

(6)

(7)

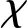
(8)

2.2 飛行約束條件

(9)

ρ(z)=ρ0ez/ξ

(10)

終端約束條件如式(11)所示，Ω是滿足終端約束的空間位置集合，(xf,yf,zf)是滑翔段結(jié)束時(shí)刻飛行器的位置坐標(biāo)，hf是終端高度約束，df是滑翔段結(jié)束時(shí)刻飛行器與目標(biāo)點(diǎn)的距離約束。

Ω={(xf,yf,zf)||zf|≥hf,

((xf-xt)2+(yf-yt)2)1/2≤df}

(11)

3 平衡滑翔傾側(cè)角影響分析

3.1 飛行速度和高度解析解

由平衡滑翔條件式(4)可得，

Lcosε=mg0cosγ

(12)

將式(2)代入式(12)可得，

(13)

所以可推導(dǎo)出飛行速度表達(dá)式為，

(14)

將式(10)代入式(14)可得，

(15)

將式(15)整理可得，

(16)

式(16)對(duì)z求微分可得，

(17)

將式(16)代入式(17)可得，

(18)

又因?yàn)椋?/p>

(19)

將式(1)代入式(19)可得，

(20)

由式(18)和式(20)可得，

(21)

將式(2)、(13)代入式(21)可得，

(22)

由式(22)可得飛行速度-傾側(cè)角解析式，

(23)

所以飛行速度是關(guān)于傾側(cè)角ε的偶函數(shù)。為方便討論，參考文獻(xiàn)[15]中傾側(cè)角的取值。

式(23)兩邊對(duì)傾側(cè)角ε求微分可得，

(24)

文獻(xiàn)[16]已經(jīng)證明速度傾角為負(fù)的小量，所以在同一攻角、同一速度傾角條件下，傾側(cè)角越大，所需飛行速度越大。

V(ε)為關(guān)于ε的單調(diào)遞增函數(shù)，所以其反函數(shù)一定存在，且也為單調(diào)遞增函數(shù)，如式(25)所示。參考文獻(xiàn)[5]中的結(jié)論，以最大升阻比攻角平衡滑翔，參考文獻(xiàn)[16]中最大升阻比的取值，CL/CD=2.98,Vmin為Ma5，所以γ∈[-1.4717°,0°)。

(25)

由式(14)和式(23)可得，

(26)

對(duì)式(26)進(jìn)行整理可得，

(27)

由式(10)和式(27)可得，

(28)

對(duì)式(28)整理可得高度-傾側(cè)角解析式，

(29)

式(29)兩邊對(duì)傾側(cè)角ε求微分可得，

(30)

將式(29)代入式(30)可得，

(31)

3.2 過程約束解析解

對(duì)式(9)中駐點(diǎn)熱流密度計(jì)算公式整理可得：

(32)

將式(14)代入式(32)整理可得，

(33)

將式(27)代入式(33)可得熱流密度-傾側(cè)角解析式，

(34)

(35)

將式(34)代入式(35)可得，

(36)

對(duì)式(36)整理可得，

(37)

因?yàn)棣谩蔥-1.4717°,0°)，sinγ∈[-2.57×10-3,0)，所以將sin γ近似為零[16-17]，式(37)可化為，

(38)

將式(2)、式(13)代入式(9)可得動(dòng)壓-傾側(cè)角解析式，

(39)

式(39)兩邊對(duì)傾側(cè)角ε求微分可得，

(40)

因?yàn)棣谩蔥-1.4717°,0°)，cosγ∈[0.9996,1)，所以cosγ≈1，式(39)可化為[16-17]，

(41)

將式(2)代入式(9)可得，

(42)

將式(13)代入式(42)整理可得過載-傾側(cè)角關(guān)系式，

(43)

式(43)兩邊對(duì)傾側(cè)角ε求微分可得，

(44)

因?yàn)棣谩蔥-1.4717°,0°)，cosγ∈[0.9996,1)，所以cosγ≈1，式(43)可化為[16-17]，

(45)

所以由式(41)、式(45)可知，當(dāng)傾側(cè)角及攻角確定時(shí)，飛行器的動(dòng)壓和過載基本保持不變。

3.3 仿真校驗(yàn)

以洛克希德-馬丁公司開發(fā)的高超聲速通用氣動(dòng)飛行器CAV-H(Common Aero Vehicle)為例[18]。

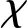
圖1(a)為5個(gè)平衡滑翔彈道的三維彈道軌跡圖，圖1(b)為5個(gè)平衡滑翔彈道的橫向平面彈道軌跡圖。

圖1 平衡滑翔彈道軌跡仿真圖Fig.1 Simulation diagram of equilibrium glide trajectory

3.3.1飛行速度和高度分析

表1是平衡滑翔各彈道速度解析解與數(shù)值解、高度解析解與數(shù)值解之間的最大絕對(duì)誤差和最大相對(duì)誤差表。從表1可以看出，5個(gè)彈道的速度解析解與數(shù)值解的最大絕對(duì)誤差小于131 m/s、最大相對(duì)誤差小于2%。5個(gè)彈道的高度解析解與數(shù)值解的最大絕對(duì)誤差小于310 m、最大相對(duì)誤差小于0.6%。由表1可知，平衡滑翔速度和高度的解析解具有較高的精度，能夠作為飛行速度和高度的近似解。

圖2是平衡滑翔各彈道的速度解析解與數(shù)值解、高度解析解與數(shù)值解的誤差曲線圖。從圖2可以看出，隨著飛行過程的進(jìn)行，速度解析解與數(shù)值解的誤差、高度解析解與數(shù)值解的誤差都震蕩收斂于0。飛行速度和高度的解析解作為一種近似解，圍繞數(shù)值解上下波動(dòng)，隨著飛行過程的進(jìn)行，解析解收斂于數(shù)值解。

表1 平衡滑翔速度和高度的解析解與數(shù)值解誤差Table 1 The error between analytic solution and numerical solution of equilibrium glide speed and altitude

圖3是平衡滑翔各彈道的速度和高度變化曲線圖。對(duì)比彈道2和彈道3、彈道4和彈道5可知，在相同機(jī)動(dòng)樣式、不同傾側(cè)角情況下，初始速度相同時(shí)，傾側(cè)角越大，阻力越大，飛行速度下降越快，同一時(shí)刻相應(yīng)彈道的飛行速度越小、高度越低。對(duì)比彈道2和彈道4、彈道3和彈道5可知，在相同傾側(cè)角、不同機(jī)動(dòng)樣式情況下，初始速度相同時(shí)，飛行速度和高度的變化與機(jī)動(dòng)樣式無關(guān)。

圖2 平衡滑翔速度和高度誤差曲線圖Fig.2 Error curve of equilibrium glide speed and altitude

圖3 平衡滑翔速度和高度變化曲線圖Fig.3 Curve of speed and altitude of equilibrium glide

3.3.2過程約束分析

表2是平衡滑翔各彈道過程約束解析解與數(shù)值解之間的最大絕對(duì)誤差和最大相對(duì)誤差表。從表2可以看出，5個(gè)彈道的熱流密度解析解與數(shù)值解的最大絕對(duì)誤差小于40 kW/m2、最大相對(duì)誤差小于5%。動(dòng)壓解析解與數(shù)值解的最大絕對(duì)誤差小于280 Pa、最大相對(duì)誤差小于0.6%。過載解析解與數(shù)值解的最大絕對(duì)誤差小于8×10-3、最大相對(duì)誤差小于0.6%。由表2可知，平衡滑翔彈道過程約束的解析解精度較高，能夠用來估算飛行過程中過程約束的大小。

圖4是平衡滑翔各彈道的過程約束解析解與數(shù)值解的誤差曲線圖。圖4(a)是平衡滑翔各彈道的熱流密度解析解與數(shù)值解的誤差曲線圖。從圖4(a)可以看出，隨著飛行過程的進(jìn)行，熱流密度解析解與數(shù)值解的誤差震蕩收斂于0，解析解作為一種近似解，圍繞數(shù)值解上下波動(dòng)，逐漸收斂于數(shù)值解。

圖4(b)和圖4(c)分別是平衡滑翔各彈道的動(dòng)壓解析解與數(shù)值解的誤差曲線圖、過載解析解與數(shù)值解的誤差曲線圖。從圖4(b)和圖4(c)可以看出，隨著飛行過程的進(jìn)行，動(dòng)壓解析解與數(shù)值解的誤差、過載解析解與數(shù)值解的誤差均呈現(xiàn)變大的趨勢(shì)。因?yàn)閯?dòng)壓和過載的解析解在計(jì)算過程中將cosγ近似為1，而實(shí)際飛行過程中速度傾角是緩慢變小的，所以動(dòng)壓和過載的解析解與數(shù)值解之間存在一定誤差。但動(dòng)壓解析解與數(shù)值解的相對(duì)誤差較小，小于0.6%；過載解析解與數(shù)值解的絕對(duì)誤差較小，在10-3量級(jí)

表2 平衡滑翔過程約束的解析解與數(shù)值解誤差Table 2 The error between analytic solution and numerical solution of equilibrium glide process constraints

圖4 平衡滑翔過程約束誤差曲線圖Fig.4 Error curve of equilibrium glide process constraints

。

圖5是平衡滑翔各彈道的過程約束變化曲線圖。圖5(a)是熱流密度變化曲線圖，對(duì)比彈道2和彈道3、彈道4和彈道5可知，在相同機(jī)動(dòng)樣式、不同傾側(cè)角情況下，初始速度相同時(shí)，傾側(cè)角越大，阻力越大，飛行速度下降越快，相應(yīng)彈道的熱流密度下降越快。對(duì)比彈道2和彈道4、彈道3和彈道5可知，在相同傾側(cè)角、不同機(jī)動(dòng)樣式情況下，熱流密度的變化與機(jī)動(dòng)樣式無關(guān)。

圖5 平衡滑翔過程約束變化曲線圖Fig.5 Curve of equilibrium glide process constraints

圖5(b)和圖5(c)是動(dòng)壓和過載變化曲線圖。對(duì)比彈道2和彈道3、彈道4和彈道5可知，在相同機(jī)動(dòng)樣式、不同傾側(cè)角情況下，初始速度相同時(shí)，傾側(cè)角越大，為平衡重力，所需空氣密度越大、飛行高度越低，相應(yīng)彈道的動(dòng)壓、過載越大。對(duì)比彈道2和彈道4、彈道3和彈道5可知，在相同傾側(cè)角、不同機(jī)動(dòng)樣式情況下，動(dòng)壓和過載的變化均與機(jī)動(dòng)樣式無關(guān)。

4 跳躍滑翔傾側(cè)角影響分析

跳躍滑翔彈道不滿足平衡滑翔條件，因此無法通過理論推導(dǎo)得出飛行速度、飛行高度、過程約束與傾側(cè)角之間的解析式。以CAV-H為例，采用數(shù)值仿真的方法分析傾側(cè)角對(duì)飛行速度、飛行高度、過程約束的影響。

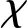
圖6(a)為5個(gè)跳躍滑翔彈道的三維彈道軌跡圖，圖6(b)為5個(gè)跳躍滑翔彈道的橫向平面彈道軌跡圖。

圖6 跳躍滑翔彈道軌跡仿真圖Fig.6 Simulation diagram of skip glide trajectory

4.1 飛行速度和高度分析

跳躍滑翔彈道的飛行器速度、高度變化曲線如圖7所示。由圖7可知，彈道7和彈道9、彈道8和彈道10的速度、高度變化曲線基本重合，說明飛行速度、高度變化均與機(jī)動(dòng)樣式無關(guān)。對(duì)比彈道7和彈道8、彈道9和彈道10可知，在相同初始速度情況下，傾側(cè)角越大，阻力越大，飛行速度下降越快，飛行高度波動(dòng)變化幅度越小，同一時(shí)刻相應(yīng)彈道的飛行速度越小、飛行高度越低。

圖7 跳躍滑翔速度和高度變化曲線圖Fig.7 Curve of skip glide speed and altitude

4.2 過程約束分析

跳躍滑翔彈道過程約束變化曲線如圖8所示。由圖8可知，彈道7和彈道9、彈道8和彈道10的熱流密度、動(dòng)壓、過載變化曲線基本重合，說明熱流密度、動(dòng)壓和過載等過程約束的變化與機(jī)動(dòng)樣式無關(guān)。對(duì)比彈道7和彈道8、彈道9和彈道10的過程約束的變化曲線可知，在相同初始速度情況下，傾側(cè)角越大，阻力越大，飛行高度波動(dòng)變化幅度越小，飛行高度對(duì)應(yīng)的空氣密度波動(dòng)變化幅度越小，相應(yīng)彈道過程約束的波動(dòng)變化幅度越小。

圖8 跳躍滑翔過程約束變化曲線圖Fig.8 Curve of skip glide process constraints

5 結(jié) 論

通過理論推導(dǎo)和數(shù)值仿真的方法分別對(duì)平衡滑翔和跳躍滑翔兩種情況下，傾側(cè)角對(duì)飛行速度、飛行高度、過程約束的影響進(jìn)行了分析。

采用平衡滑翔彈道滑翔時(shí)，通過理論推導(dǎo)得出了飛行速度、飛行高度、過程約束與傾側(cè)角之間的解析式。數(shù)值仿真結(jié)果表明,理論推導(dǎo)得出的解析解具有較高的精度，可用于數(shù)值解的近似計(jì)算。解析解作為一種近似解，可用來分析飛行速度、飛行高度和過程約束的變化規(guī)律。在平衡滑翔條件下，飛行速度、飛行高度和過程約束的變化均與機(jī)動(dòng)樣式無關(guān)。在相同初始速度情況下，傾側(cè)角越大，相應(yīng)彈道飛行速度、飛行高度、熱流密度下降越快，動(dòng)壓和過載越大。

采用跳躍滑翔彈道滑翔時(shí)，飛行速度、飛行高度和過程約束的變化均與機(jī)動(dòng)樣式無關(guān)。在相同初始速度情況下，傾側(cè)角越大，飛行速度下降越快，同一時(shí)刻相應(yīng)彈道的飛行速度越小、飛行高度越低，飛行高度和過程約束的波動(dòng)變化幅度越小。

不管是平衡滑翔還是跳躍滑翔，飛行速度、飛行高度和過程約束都與機(jī)動(dòng)樣式無關(guān)，而與傾側(cè)角有關(guān)。機(jī)動(dòng)樣式主要對(duì)橫向機(jī)動(dòng)距離和彈道變軌有影響，而傾側(cè)角對(duì)橫向機(jī)動(dòng)距離和彈道變軌影響如何則有待于進(jìn)一步研究。