始發保優的序列比對

陸 成 剛

(浙江工業大學 理學院，杭州 310023)

E-mail：luchenggang168@gmail.com

1 引 言

序列比對是矢量聚類或模式分類的基礎，它的核心功能是計算模式之間的相似(異)性的程度.無論哪一種聚類分類方法，本質上都要基于某種內置的距離運算.常規的歐幾里德距離可以看作是一種靜態的序列比對，而經典的DTW距離(DTW英文全稱Dynamic Time Warping即動態時間規整)則以動態對齊模式的距離計算而聞名[1-3].數學上可以證明，DTW距離并不符合距離公理的三角形法則(但滿足非負性、對稱性法則)，所以它并不支持使用算術平均來計算多個矢量的質心(距離滿足三角形法則是使用算術平均計算該距離意義下質心的必要條件)，也因此在k均值聚類、模糊c均值聚類等領域應用受到限制[4,5].事實上，在DTW對齊模式下求兩個矢量的算術平均是可以得到它們的(基于DTW距離意義下的)質心的，只是對于三個以上的矢量求它們的動態對齊方式是比較困難的，這就是所謂的動態規劃算法的“維數災難”問題[6-8].在兩個序列之間使用DTW計算距離具有一些不可多得的優勢，如能適應序列在時間軸上的伸縮變異，又能適應參與比較的兩個序列長度不一致的情況.在層次聚類、kNN近鄰法、PCA聚類、譜聚類和DBSCAN聚類法中只涉及計算兩兩之間的序列距離[9-13]，因而都可以使用DTW距離作為內置.

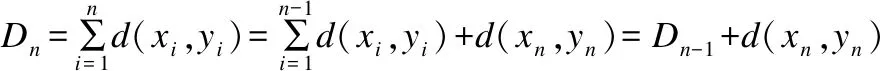
2 DTW的重新理解

2.1 DTW距離

DTW是使用動態規劃方法搜尋序列間足標的一種最佳對應使它們具有最小的距離.DTW距離主要使用在評估兩個數據序列之間的相似性上.特別是基于DTW距離的kNN匹配分類法一度是近十幾年間序列分類識別應用領域的經典標配[16-18].如圖1示例了常規歐幾里德距離的靜態對應和DTW距離的動態對應之間的差異：前者具有平行平均的對應間隔、后者完全是不規則對應的.

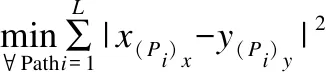
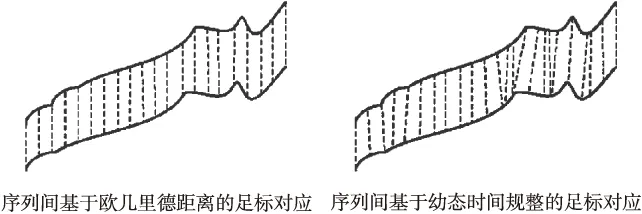
圖1 DTW動態時間規整具有捕捉序列時長動態差異的特性

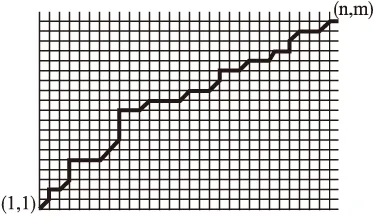
圖2 坐標軸點陣的路徑

傳統的DTW距離算法是基于動態規劃原理進行的，引入狀態變量D(i,j)表示由P1=(1,1)到點(i,j)的最小距離，于是D(n,m)就是所求的DTW距離.狀態變量D(i,j)有遞推式D(i,j)=min{D(i-1,j-1),D(i-1,j),D(i,j-1)}+d(i,j)其中d(i,j)=|xi-yj|2或d(i,j)=|xi-yj|.根據遞推公式生成狀態矩陣(D(i,j))m×n，其中首行首列通過其唯一前鄰點來生成，取得最小值的最優路徑由終點(n,m)逆溯到起點(1,1)而得到.取得路徑的逆溯過程的偽碼如下.

1) Path=NULL,(n,m)→Path;

2)i=n,j=m;

while(i>1 or j>1)

{

if(i==1) j=j-1;

else if(j==1) i=i-1;

else i, j get value from

min{D(i-1,j-1),D(i,j-1),D(i-1,j)};//將最小者對應的足標賦給i、j

(i,j)→Path;

}

3) Inverse(Path);//將Path中各點倒序;

2.2 DTW更新解讀

DTW距離求解法是基于狀態變量的遞推方程施行的，而遞推方程成立是利用了平方距離或曼哈頓距離的累計可加性.利用距離形式的累計可加性可以得出達到最優值的路徑也具有保持最優性的可加性(簡稱可加保優性)，這就是定理1.

首先介紹路徑全分割：如圖3中路徑Path={P1,P2,…,PL}分割成多個片段，每個片段稱謂子路徑(Subpath)，前后相鄰的子路徑共享一端點，所有子路徑的依次串接(共享的端點只計一點)恢復為原路徑.

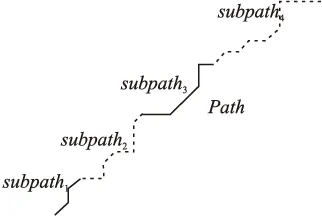
圖3 路徑的全分割示意圖：路徑Path被分割為4段子路徑Subpath，且第一條子路徑的起點P1，第4條子路徑的終點PL

定理1.設Path={P1,P2,…,PL}是DTW距離的(最優)路徑，則對該路徑的任何一個全分割，每條子路徑都是其自身起點到其自身終點的最優路徑.反之，Path={P1,P2,…,PL}的任意一個全分割的每條子路徑都是其起點到其終點的最優路徑，則Path={P1,P2,…,PL}是DTW距離的(最優)路徑.

證明：先證前面的結論，使用反證法，假設{Pi,Pi+1,…,Pj}?{P1,P2,…,PL}是一條子路徑，并且{Pi,Pi+1,…,Pj}不是序列(x(Pi)x,x(Pi)x+1,…,x(Pj)x)和(y(Pi)y,y(Pi)y+1,…,y(Pj)y)間DTW距離對應的最優路徑.求得它們的DTW距離對應的路徑不妨設為{Pi′,Pi′+1,…,Pj′}其中Pi′=Pi且Pj′=Pj，則{P1,P2,…,Pi-1,Pi′,Pi′+1,…,Pj′,Pj+1,…,PL}對應的距離數值應小于Path={P1,P2,…,PL} 對應的距離數值，這與Path={P1,P2,…,PL}是DTW距離對應的(最優)路徑矛盾.再證后面的結論，反之，Path={P1,P2,…,PL}本身也是它自己的一個全分割，它是最優路徑，所以它是DTW距離的(最優)路徑.證畢.

引入始發路徑的概念：以端點(1,1)為起點的路徑稱為始發路徑.如果對路徑上任意點作終點的始發路徑都是從(1,1)到該點的最優路徑，則稱該路徑具有始發保優性.DTW距離路徑即具始發保優性，此為推論1.

推論1.設Path={P1,P2,…,PL}是DTW距離的(最優)路徑，則以該路徑上任意點作終點的始發路徑都是從(1,1)到該點的最優路徑.反之，如果Path={P1,P2,…,PL}滿足這樣的性質：以該路徑上任意點作終點的始發路徑都是從(1,1)到該點的最優路徑，則Path={P1,P2,…,PL}是DTW距離的(最優)路徑.

證明：在Path={P1,P2,…,PL}任取一點作始發路徑的終點，則該始發路徑與以該點作起點、(n,m)為終點的子路徑構成原路徑的全分割，根據定理1，該始發路徑為最優路徑.反之是顯然的.證畢.

圖4示意了始發最優特性，一條最優路徑上任意點作終點的框內部分(路徑)都是最優的.

圖4 始發最優示意

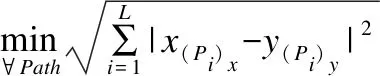
3 DTW距離的缺陷

傳統的DTW距離隱含著一種缺陷，例如考慮使用DTW距離計算以下三段直流信號的匹配情況：A=(0.1,0.1)、B=(0.25,0.25,0.25,0.25)、C=(0.28,0.28,0.28)，信號A與B的DTW距離為0.6，其最優匹配路徑的長度為4；而信號C與A的DTW距離0.54，最優匹配路徑的長度為3.從我們直覺判斷信號B比信號C更接近A，但從DTW距離決定的相異性來看，反而是C比B更接近A.造成這個反直覺的效果是由于我們僅僅考慮了距離，而忽視了路徑長度，假如以DTW距離相對路徑長度的平均值而言，B比C更接近A.傳統DTW的缺陷是沒有考慮路徑長度平均的距離，從而可能導致兩個同類序列的距離大于兩個異類序列的距離.這就違背了“距離大小決定相異程度”的準則.定理2從理論上揭示了這種可能性.

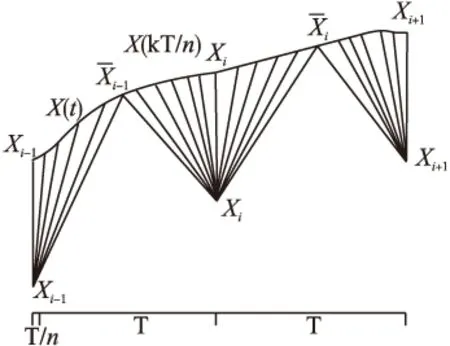
圖5 信號重構采樣后的DTW匹配

定理2.設對于序列S1其采樣周期為T，先將S1使用sinc插值恢復成模擬信號，再使用T/n的采樣周期離散化形成序列S2，S2長度n倍于S1、但兩者仍屬同類序列，可證S1和S2的DTW距離隨著n的增加而無限制增加，勢必將大于S1與任一確定的其它類序列H的DTW距離.

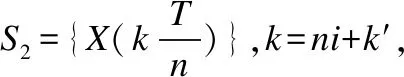
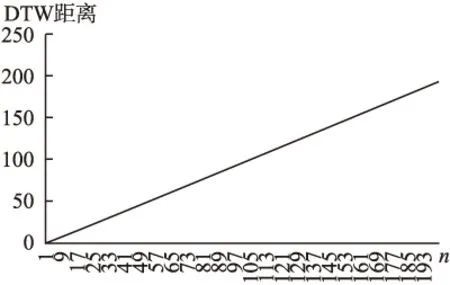
圖6 同類序列DTW距離隨著長度差異變大而變大

可見考慮路徑長度平均意義下的DTW距離是必要的，而這又牽涉到對于不滿足累計可加特性的距離形式的處理.

4 基于始發保優的延拓

對序列X=(x1,x2,…,xn)與Y=(y1,y2,…,ym)，定義滿足端點條件、連續性和單調性的足標對應的路徑Path={P1,P2,…,PL}，提出三個組合優化問題

(1)

(2)

(3)

顯然平均距離、Pearson相關系數和Tanimoto系數不滿足累計可加性，組合優化問題式(1-3)的最優解沒有保優可加性結構.由于始發保優特性易于算法實施，受此啟發，提出修正的最優路徑問題.考慮任意的終點為(μ,υ)的始發路徑，記作Path(μ,υ)，由此對應的三個組合優化問題衍生為三族問題，即

(4)

(5)

(6)

式(4-6)是三族優化問題，每族都考慮為μ=1,2,…,n;υ=1,2,…,m遍歷整個點陣時的一系列組合優化問題，由此開發的算法稱為始發保優的序列比對.當只考慮(μ,υ)=(n,m)時式(4-6)蛻化為式(1-3)，可以理解為式(4-6)的解路徑是式(1-3)的解路徑附加滿足始發保優性質的解路徑.

由式(4-6)求得的系數不妨稱作動態平均距離、動態Pearson系數和動態Tanimoto系數，照例它們滿足距離公理的非負性法則和對稱性法則，且序列X=Y時動態平均距離為0，而動態Pearson系數和動態Tanimoto系數均為1.

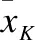
lij：表示(x1,x2,…,xi)與(y1,y2,…,yj)依始發最優特性計算絕對值最大Pearson相關系數時得到的對應路徑的長度；

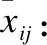
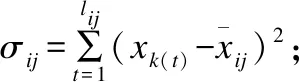
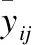
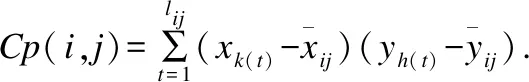
再引入這些統計量的累計計算公式，設(i′,j′)是當前點(i,j)的一個后繼，即(i′,j′)=(i+1,j)或者(i′,j′)=(i,j+1) 或者(i′,j′)=(i+1,j+1)，則

li′j′=lij+1

(7)

(8)

(9)

(10)

(11)

(12)

以上諸公式中式(7)是顯然的，式(8、10)是均值累計計算原理的應用；式(9、11)本質上也是均值的累計計算，只是在應用式(8、10)結果基礎上再進行累計計算；式(12)是內積的累計計算，可以通過內積的定義直接驗證.由此得到(i′,j′)的絕對值Pearson相關系數

(13)

下面給出以式(5)作例子的動態Pearson系數算法，其它兩族問題的算法類推可得.

動態Pearson系數算法

2.令k=1，h=2,3,…,m；l1h=l1h-1+1，

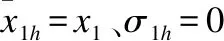
c1h=0

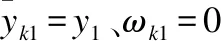
ck1=0

4.令k=2,3,…,n，h=2,3,…,m；

當(u,v)遍歷{(k-1,h-1),(k-1,h),(k,h-1)}得到三個|ctemp|中取最大的一個(在計算動態平均距離時取最小的一個，而動態Tanimoto系數也是取最大)，此時(u,v)=(u0,v0)為{(k-1,h-1),(k-1,h),(k,h-1)}里的具體的一個格點.因而利用式(7-13)更新矩陣元素如下

lkh=lu0v0+1

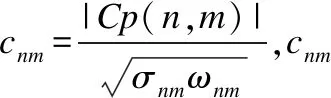
6.對其它兩族優化問題可以施行同樣的算法，這類算法可以總結為如圖7的四個模塊：首先是初始化，如以上算法的步驟1；其次對涉及到的統計量構成的矩陣更新其首行首列，如以上步驟2、3；然后依據式(7)-式(13)的累計計算原理更新矩陣的其余部分，如以上步驟4；最后是輸出結果如以上步驟5.

圖7 動態系數算法框架

Fig.7 Algorithm framework for dynamic mode

圖8-圖10示例了DTW距離與動態平均距離、Pearson系數與動態Pearson系數、以及Tanimoto系數和動態Tanimoto系數的執行效果的比較：

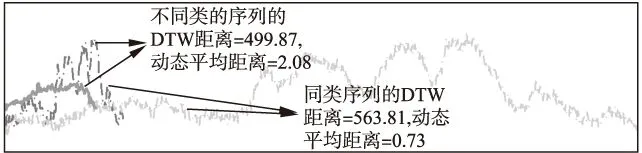
圖8 DTW距離與動態平均距離的比較

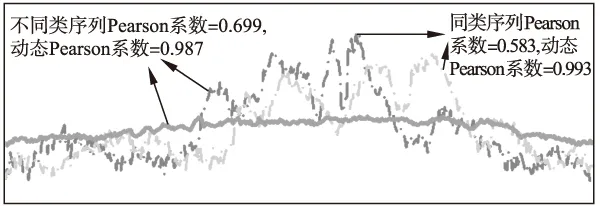
圖9 Pearson系數與動態Pearson系數的比較

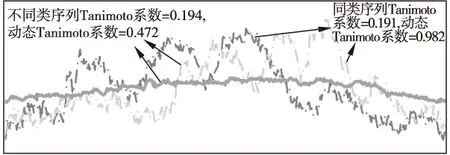
圖10 Tanimoto系數與動態Tanimoto系數的比較

在圖8-圖10中點劃線示例的是同一類序列，粗實線代表另外一類.圖8的DTW距離和動態平均距離的示例顯示相同類別的序列距離反而比不同類別的序列的距離遠，而動態平均距離則能正常地顯示同類距離近、異類遠.造成DTW距離度量失效的原因是DTW距離對序列長度分布的不均勻程度比較敏感，從而引入了路徑長度對距離數值的干擾.主要表現在同類的序列、但長度相差較大時，DTW距離的數值較大，“掩蓋”了它們本該相似的屬性.在算法測試部分，更多的序列測試證實了動態平均距離優于DTW距離.圖9、圖10使用長度相同的序列作比較，常規Pearson系數和Tanimoto系數均在同類序列顯示值為小、而異類序列值為大，動態計算的Pearson系數和Tanimoto系數能有效地“糾正”這個反常現象.

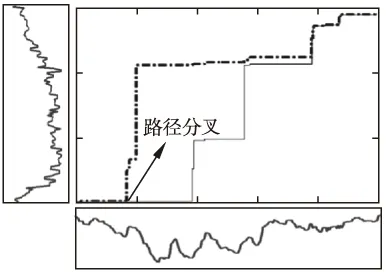
圖11 動態平均距離的最優路徑不滿足可加保優性

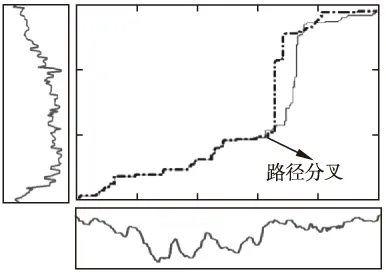
圖12 動態Pearson系數的最優路徑不滿足可加保優性

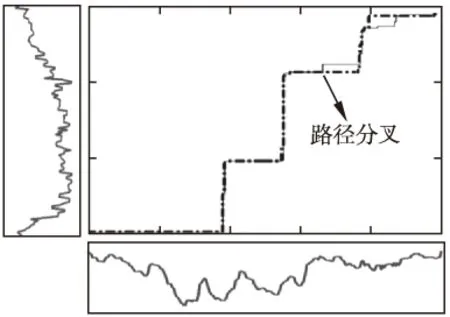
圖13 動態Tanimoto系數的最優路徑不滿足可加保優性

式(4-6)是始發保優原則衍生的三族優化問題，但解路徑依舊沒有傳統DTW路徑的可加保優特性.假如在依式(4-6)的最優模式中獲得的全局最優路徑上任意取定一點，以此為界，構造一個分割，那么從始發點到該點的最優路徑與全局最優路徑的前部分重合，而由該點到終點的最優路徑與全局最優路徑的后部分不一致，產生分叉.圖11-圖13分別示例了這個由分割點產生路徑分叉的現象.它證實了基于式(4-6)的序列比對法滿足始發保優，但不滿足可加保優特性.

最后對DTW距離、動態平均距離、動態Pearson系數、和動態Tanimoto系數進行算法復雜度分析，主要考慮算法框架中涉及到的矩陣變量的數目，因為它既關聯到緩存占用大小，又關聯到更新矩陣元素的計算量.這里不考慮臨時變量、輔助變量、以及編程時各種數據類型占用內存的差異.由于輸入序列段長分別是m和n，所以一個矩陣變量的資源數目就是mn，它既是緩存開銷的大小，也是計算量級.表1顯示了四類方法的計算資源的消耗量級.易知，DTW只需更新距離矩陣，所以是1個mn單位，而動態平均距離除了距離矩陣外，還需要更新路徑長度矩陣，所以是2個mn單位；動態Pearson方法包含路徑長度矩陣、序列X和Y的均值以及方差的矩陣、內積矩陣和Pearson系數矩陣共7個mn單位，類似可得動態Tanimoto系數方法的復雜度是3個mn單位.

表1 四類比對方法的計算復雜度比較

Table 1 Computation complexity comparing for 4 alignment methods

比對方法DTW動態平均距離動態Pearson動態Tanimoto內存消耗mn2mn7mn3mn計算量級mn2mn7mn3mn

5 動態平均距離的算法測試

相對來說動態平均距離具有最接近原始DTW方法的計算資源占用效率，而且兩者皆是距離屬性，可比度強，在算法測試階段專門以動態平均距離作代表與DTW作算法效果比較.實驗數據來源于國家環保部設立在浙江省環保廳的全國電離輻射測量監測中心.測試集是包含4298例環境電離輻射時間序列的波峰樣本，它們已經被人工標注為4類.序列集的平均長度為237.94點，根差為96.78，可見數據長度的分布有較大的不均勻性.這原因其一是由于波峰段檢測提取技術的限制，造成波峰前后帶有較多或較少的平緩部分；其二是電離輻射劑量波峰本身由于環境因素如持續時長不一的降水會導致波峰長短不一的現象.我們采用層次聚類法分別以DTW距離和動態平均距離作內置進行聚類，層次由底層向上層演進，聚類循環的停機閾值為類數4.

圖14 序列聚類算法的計數統計矩陣

如圖14(a)所示DTW距離內置的聚類結果統計，計數矩陣的非對角元數目較大，這表示算法的漏檢率、虛警率都較高；而圖14(b)顯示動態平均距離作內置的層次聚類執行效果較好，計數矩陣的非對角元數目較小.由表2統計DTW距離的平均F值僅為61.1%，而動態平均距離可達到的平均F值為96.9%，平均F值比前者竟高達35.8%.通過對于4298例已標注數據的算法測試，相對于DTW距離，就平均F值來說動態平均距離對算法性能的提升在35個百分點以上.

表2 對4298例序列進行層次聚類的定量分析

Table 2 Quantity analysis based on hierarchy clustering for 4298 samples

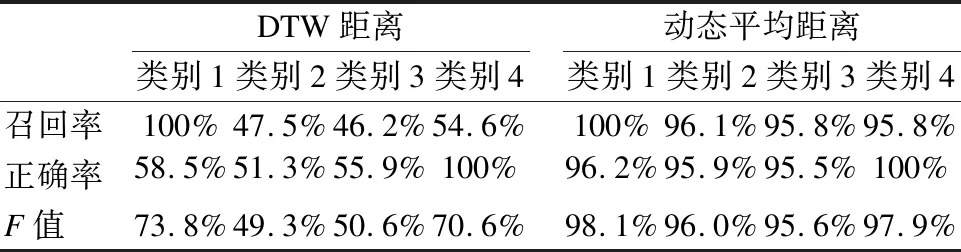
DTW距離類別1類別2類別3類別4動態平均距離類別1類別2類別3類別4召回率100%47.5%46.2%54.6%100%96.1%95.8%95.8%正確率58.5%51.3%55.9%100%96.2%95.9%95.5%100%F值73.8%49.3%50.6%70.6%98.1%96.0%95.6% 97.9%

另使用6182例4類別波峰段的標注數據集進行kNN最近鄰法分類測試，該數據集段長平均為180.7、根差為168.9.且與前面4298例數據集不同的是每條測試數據均含有外點成份，如圖15所示.電離輻射檢測儀器故障自動重啟、分布式監測網絡數據傳輸中斷等設備異常會造成電離輻射時間序列夾雜一定的隨機外點或噪聲.作為kNN法模板庫的樣本采用當前全部被測數據集合之外的波峰段、且經人工挑選而一律不含隨機外點成份.

圖15 6182例4種含外點的波峰段類型示例，其中3個外點是突降型，另外一個突升型

從表3看出在6182例數據集所含具有較懸殊的信號長度差別的動態特性下，將DTW距離和動態平均距離用于kNN模式分類時，后者的識別精度顯著地優于前者.

表3 對6182例數據集進行kNN近鄰法分類的定量分析

Table 3 Quantitative analysis of k nearest neighbor classification for 6182-samples set

類別DTW距離類別1類別2類別3類別4動態平均距離類別1類別2類別3類別4F值96.4%94.4%95.3%94.1%99.7%99.8%99.7%99.8%

表4 對杭州50年降雨數據進行kNN近鄰法的豐澇旱適分類

Table 4 Classification of the drought and waterlogging in the 50-year rainfall data of Hangzhou using the kNN

類別DTW距離澇豐適少動態平均距離澇豐適少F值98.6%99.2%97.8%96.4%99.8%99.4%99.6%99.2%

電離輻射波峰跟降雨及降雨持續時間有關，另考慮杭州近50年各年份日降雨量序列數據集，對部分整月數據進行雨澇、豐水、適中和少雨等四個類型標注，并對其余整月數據進行kNN近鄰法分類，然后對分類結果進行人工核驗，所得F值分析為表4，顯然動態平均距離內置的分類器更優.

6 總 結

數據序列的比對是模式聚類和識別的基礎，而遍歷數據的方式又是序列比對的基礎.以DTW距離為代表的數據動態對齊方式是一類行之有效的數據遍歷方式，它突破了傳統靜態距離計算的局限，不僅能適應時長不一致的序列比對，更能捕捉到數據時長伸縮的差異.如何將動態比對下的距離計算拓展到非一般距離，如平均距離、Pearson相關系數、和Tanimoto相似系數等，是一個有趣而實用的課題.我們的研究工作圍繞著距離形式失去累計可加性時，如何使用類似DTW算法的結構去計算動態平均距離、動態Pearson系數和動態Tanimoto系數，提出了始發保優的概念，并將其施行于算法的設計，創建了一系列的序列比對方法.并以算法復雜度最低的動態平均距離作代表進行大量標注數據集的層次聚類測試，算法執行效果較DTW內置的聚類法整體性能提升了35個百分點以上.且在使用kNN進行序列匹配分類測試時內置動態平均距離較DTW距離仍能取得更高的精度.將來如何將動態平均距離內置到k均值聚類是一個更值得期待的工作.文獻[4,5]使用類似最大期望法進行基于DTW距離的k均值聚類中心的生成，這個方法同樣適用于基于動態平均距離的k均值聚類.我們計劃實現這種聚類方法，并且基于動態平均距離比DTW距離更吻合“距離大小決定相異程度”的原則，從而期待證明動態平均距離在無監督聚類上比DTW距離具有更優越的表現.