環境激勵下基于改進經驗小波變換的土木工程結構模態參數識別

萬熹 黃天立 陳華鵬

摘要：針對經驗小波變換（EWT）識別噪聲信號模態參數時，由于傅里葉頻譜易受噪聲影響而頻帶劃分不準確等問題，提出了一種基于Burg算法的自回歸功率譜替代傅里葉頻譜的信號頻帶劃分技術，結合隨機減量技術和基于Hilbert變換的單分量模態參數識別方法，提出了環境激勵下基于改進經驗小波變換的土木工程結構模態參數識別方法。典型模擬信號、美國土木工程師學會ASCE Benchmark數值模型以及臺風激勵下香港汀九斜拉橋的模態參數識別結果驗證了方法的正確性、有效性和適用性。研究結果表明：基于自回歸功率譜的信號頻帶劃分技術，可更準確地估計信號頻帶邊界，隔離噪聲;基于改進EWT方法識別的結構模態參數更準確，精度高于基于小波變換的方法，且能有效地識別環境激勵下實際土木工程結構的低階自振頻率和阻尼比。

關鍵詞：模態參數識別;土木工程結構;斜拉橋;經驗小波變換;Benchmark模型

中圖分類號：TU311.3;U448.27文獻標志碼：A 文章編號：1004-4523（2020）02-0219-12

DOI：10.16385/j.cnki.issn.1004-4523.2020.02.001

引言

結構模態參數識別就是從結構激勵和響應數據或僅從響應數據中獲取結構的模態參數，其常用于結構損傷識別、結構模型修正和振動控制等領域。結構模態參數識別主要包括基于頻率響應函數（FRFs）的頻域方法和基于脈沖響應函數（IRFs）的時域方法兩大類。近年來，隨著各種信號時頻分析技術的發展，如短時傅里葉變換（STFT）、wign-er-Ville分布（wVD）、小波變換（wT）、s變換、希爾伯特一黃（HHT）變換和同步壓縮小波變換（swT）等，基于時頻域的結構模態參數識別方法，特別是基于小波變換和HHT變換的模態參數識別方法得到了深入的研究，并在土木工程結構中得到了廣泛的應用。

基于小波變換的模態參數識別方法雖然具有嚴格的理論基礎，但由于其在分離多分量信號時對小波基函數及其參數的選擇比較麻煩，因此一定程度上限值了其應用。文獻[8-10]提出的基于經驗模式分解（EMD）和Hilbert變換的希爾伯特一黃變換（HHT），由于EMD分解的自適應性，其在結構模態參數識別上得到了較好的應用。但是，EMD分解中存在過包絡、欠包絡、模態混疊、端點效應以及分解不正交等問題，雖然一些學者針對EMD分解中存在的這些問題，提出了一些改進措施，如黃天立等。針對EMD分解不正交的問題提出了正交化處理措施，并有效識別了具有密集模態情況的結構模態參數等，但由于EMD分解本質為經驗分解，沒有嚴格的數學證明，很大程度限制了HHT方法在結構模態參數識別上的應用。

Gilles等結合EMD分解自適應性和小波變換理論完備性的優點，提出了一種新的多分量信號分解方法——經驗小波變換（Empirical waveletTransform，EwT）方法，EWT方法通過搜索信號傅里葉頻譜中的極大、極小值點，自適應地劃分頻譜，自動選擇小波基函數構建小波濾波器組，從而能夠從多分量信號中提取具有緊支撐特性的調幅一調頻單分量信號。EWT方法是一種建立在小波理論框架之上的自適應時頻信號處理方法，由于其理論完備和計算高效，其在結構模態參數識別、機械故障診斷和地震勘探等領域得到了迅速地推廣應用。Amezquita-Sanchez等結合多重信號分類（MUSIC）算法，采用EWT方法識別了某高層建筑結構的自振頻率和阻尼比。Yuan等結合二階盲源分離技術，采用EWT方法識別了一個具有密集模態的帶調諧質量阻尼器（TMD）多層房屋結構的固有頻率。

Gilles提出的EWT方法在識別結構模態參數時，對于簡單模擬信號或信噪比高的信號，采用基于傅里葉頻譜的頻帶劃分技術，根據其劃分的頻帶可較好地分離多分量信號的各階模態，得到滿意的結果。然而，由于傅里葉頻譜不可避免的存在頻率泄露、對噪聲敏感和虛假極值等問題，對于信噪比較低的信號，基于信號傅里葉頻譜，無論采用其提供的何種方式來劃分邊界，如局部最大值或最小值方法等，都易產生過多的和不準確的邊界，存在無法準確分離信號各階模態的問題。

針對此問題，本文提出了一種基于Burg算法的自回歸功率譜替代傅里葉頻譜的信號頻帶劃分技術，結合隨機減量技術和基于Hilbert變換的單分量模態參數識別方法，給出了環境激勵下基于改進經驗小波變換的土木工程結構模態參數識別方法。通過典型模擬信號、美國土木工程師學會ASCEBenchmark數值模型以及臺風激勵下香港汀九斜拉橋的模態參數識別分析，研究了本文方法的正確性、有效性和適用性。

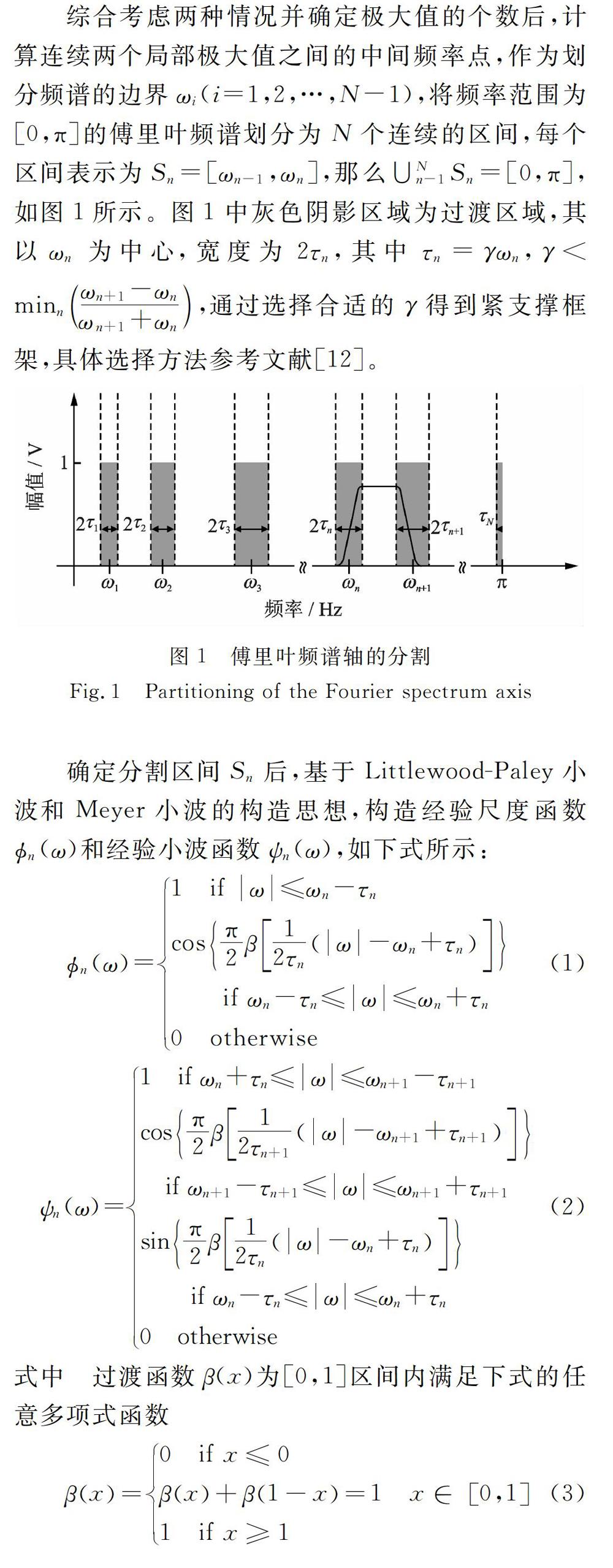
1理論基礎

1.1經驗小波變換

經驗小波變換方法對所分析的多分量信號傅里葉頻譜進行自適應劃分，同時構建一組小波濾波器組對劃分過的頻譜進行濾波，從而將多分量信號分解為一系列具有緊支撐傅里葉頻譜的調幅一調頻單分量成分。以所分析的某時域離散信號x（t）為例，為滿足Shannon準則，首先將信號的傅里葉頻譜范圍歸一化于[0，π]區問;其次，假設信號由N個單分量成分組成，對信號x（t）進行傅里葉變換得到其傅里葉頻譜X（ω），同時確定頻譜中的M個局部最大值，并將其進行降序排列。此時，考慮兩種情況：

（1）若M>N，表明信號中包含的單分量個數大于期望值N，此時保留前N個極大值;

（2）若M≤N，表明信號中包含的單分量個數小于期望值N，此時保留所有的極大值，對N值進行重置。

1.2.2基于自回歸功率譜的頻帶劃分技術

自回歸AR參數模型是全極點模型，反映的是功率譜峰值，其求解簡單、工程應用方便。相對于傅里葉頻譜，自回歸功率譜更光滑、分辨率更高，即使在有噪聲情況下，仍能很好識別每一階頻率，其功率譜密度曲線中每一個顯著的譜峰都可看作信號的一個單一模態，這為經驗小波變換方法劃分頻帶邊界提供了極大的便利。

選擇頻帶邊界時，Gilles提出了選擇頻譜兩相鄰峰值平均值作為邊界的方法，本文稱Gilles原方法，該方法對于無噪聲且信號組成分量簡單易分的信號非常有效。然而，對于含噪聲信號，由于其頻譜上存在一些噪聲引起的小峰值，使得基于Gilles方法的信號分解效果欠佳。為了減小噪聲對信號分解的影響，Amezquita-Sanchez等提出了一種改進的頻帶選擇方法，該方法采用與頻譜極大峰值相鄰的兩個極小值作為邊界，本文稱改進方法。圖2對比了上述兩種方法在頻帶邊界劃分上的區別，圖中實線為Gilles原方法，虛線為改進方法。從圖2可以看出，改進方法更好地將主要振動頻率和噪聲隔離開來，最大程度地減小了噪聲影響。

1.3隨機減量技術

隨機減量技術（RDT）是從環境激勵下結構振動響應信號中提取結構自由振動衰減響應的一種處理方法，該方法利用樣本平均，對實測振動響應信號中包含的確定性振動信號和隨機信號進行辨別，從而得到自由振動衰減信號，然后利用時域方法進行結構模態參數識別。

對一定長度的振動信號來說，在進行隨機減量指紋信號的提取過程中，觸發水平閾值A的選取至關重要。當A取值較大時，從信號中取到樣本函數的個數減少，導致隨機減量指紋中包括噪聲信息增加;如果A取值較小，雖然樣本函數的個數增多，平均次數增加，但由于其振動幅值量值較小，獲得的隨機減量指紋亦較差。為了在有限數據樣本情況下合理選取RDT觸發水平閾值，提高RDT的準確度，本文采用了兩種處理措施：（1）采用正、負閾值同時截取的方法;對于負閾值，截取子信號段，變號后參與疊加平均，使參與平均的子信號段數增加約1倍，如圖3所示;（2）通過曲線擬合方法提高樣本的采樣頻率，從而更精確地識別截取常數。

圖6（a）給出了該模擬信號的傅里葉幅值譜。從圖6（a）可以看出，模擬信號的3個峰值非常明顯且分離。因此，本文設置分解層數N=3，采用EWT自適應算法自動劃分頻帶，各頻帶邊界如圖6（a）中虛線所示。基于獲得的頻帶，EWT建立了由1個尺度函數和N個小波函數組成的小波濾波器組，模擬信號經小波濾波器組后被分解為3個單分量信號，如圖6（b）所示。從圖6（b）可以看出，經驗小波變換有效地分解出了模擬信號的各頻率信號成分，各分量之問沒有出現模態混疊，且各分量信號與構成原始模擬信號的各成分具有相同的時域信號特征。此外，由于EWT本質上仍屬于小波變換，具有小波變換的優點，因此，分解所得各分量之問具有嚴格的正交性，避免了EMD分解所得各固有模式函數之問正交性程度較差的缺點。

針對圖6（b）所示采用EWT分離出的單分量信號，采用基于Hilbert變換的單分量信號模態參數識別方法，基于線性最小二乘擬合圖7所示各分量幅值曲線和相位曲線的斜率，識別得到該模擬信號的3階頻率分別為1.0，4.993，9.992Hz，阻尼比均為1%，識別結果與理論值非常接近。

2.2ASCE Benchmark模型

為評價各種模態參數識別方法和損傷診斷方法的適用性，美國土木工程師學會提供了一個基準模型，即ASCE Benchmark模型。該模型為一個4層2×2跨的鋼框架模型，層高0.9m，單跨跨徑1.25m，其有限元模型如圖8所示。本文采用其12自由度模型，即每層僅包含x，y兩個方向的平動自由度和扭轉自由度，激勵采用高斯白噪聲模擬環境荷載作用于每層結構的y方向。圖9給出了模型第4層柱2（Column 2）的y方向加速度時程響應信號，其采樣頻率為1000Hz，信號時長為20s。

圖10（a）給出了第4層柱2（Column 2）的y方向加速度時程響應的傅里葉頻譜及其采用EWT方法檢測得到的頻帶劃分邊界，圖10（b）給出了第4層柱2（Column 2）的y方向加速度時程響應的自回歸功率譜及其相應的信號頻帶劃分邊界（邊界如圖中虛線所示）。從圖10（a）中可以看出，在低頻部分，EWT方法無法準確檢測到所有邊界，其中第1、第2階頻率被劃為到同一個頻帶中，其余各階頻率也沒有很好分離;在高頻部分，由于噪聲影響，EWT方法劃分出了若干無意義的頻帶。因此，基于EWT方法的頻帶，無法準確地提取出結構的各階模態響應。從圖10（b）可以看出，根據自回歸功率譜劃分了10階頻帶邊界，結構的前4階彎曲振動模態和前兩階扭轉振動模態被清楚的劃分到了第2，3，4，6，7和8階頻帶中。此外，圖10（b）所示第1，5，9和10階頻帶用于剔除信號噪聲而劃定，其經EWT分解所得信號不用于模態參數識別。

基于圖10（b）確定的頻帶，建立相應的小波濾波器組，通過EWT將信號分解為各單分量信號，每單分量信號代表信號的某一階模態響應。圖11給出了EWT分解所得的信號前3階分量。圖12給出了應用隨機減量技術提取的前3階分量信號的隨機減量指紋，即自由振動衰減響應。圖13給出了3階分量信號隨機減量指紋的對數幅值曲線和相位曲線，其中虛線為實際曲線，實線為基于最小二乘的擬合曲線，用于獲取相應的曲線斜率。應用基于Hilbert變換的單分量信號模態參數識別方法，識別得到結構的自振頻率和阻尼比，如表1所示。表1還給出了結構自振頻率和阻尼比的理論值和文獻[17]基于小波變換方法的識別結果。

從表1可以看出，基于改進EWT方法識別出的模態參數值與理論值非常接近，且識別出了小波變換方法未能識別的兩階扭轉模態。

3實橋應用：環境激勵下汀九斜拉橋模態參數識別

典型模擬信號和美國土木工程師學會ASCEBenchmark數值模型的模態參數識別結果驗證了基于改進EWT方法識別結構模態參數的正確性和有效性，本節進一步探討其在實際土木工程結構模態參數識別中的應用可行性。

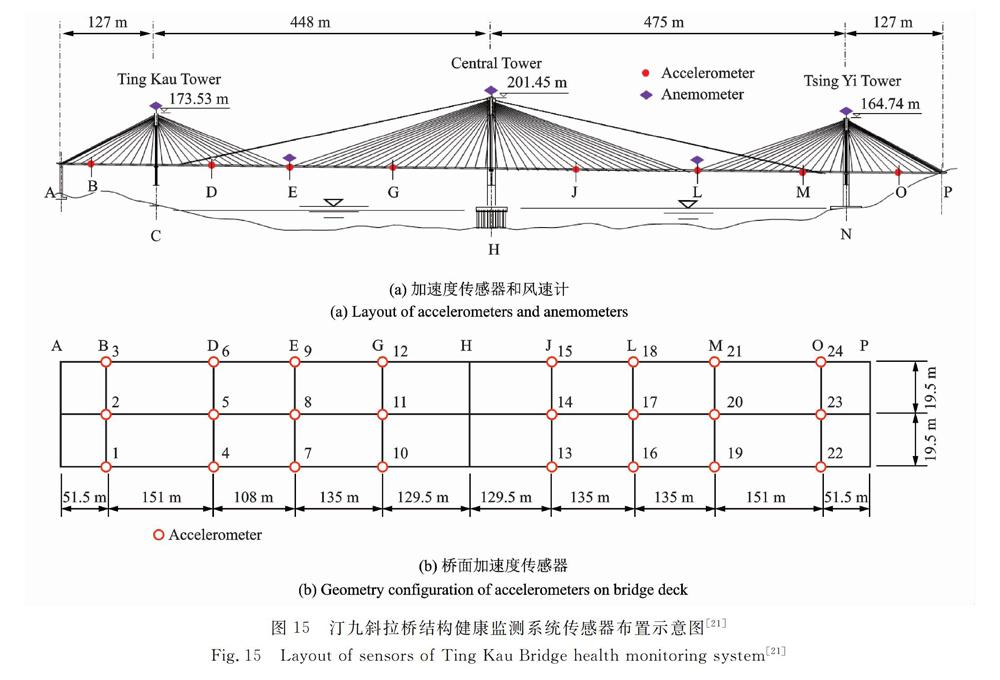
本文選取了香港汀九斜拉橋（Ting KauBridge，TKB），如圖14所示，該橋為一座三塔四跨式斜拉橋，跨越藍巴勒海峽連接汀九和青衣，其跨度為（127+448+475+127）m，塔柱高度分別為170，194和158m，橋面寬度為42.8m。汀九斜拉橋于1999年安裝有結構健康監測系統，包括測量加速度、風速、應變、位移、溫度等230多個傳感器，其中在橋面安裝有24個加速度傳感器，在3個索塔頂部和2個中跨跨中橋面安裝有7個風速儀，傳感器的詳細布置如圖15所示。

表2給出了汀九斜拉橋結構健康監測系統采集到的臺風激勵下橋面振動加速度響應信號數據，各數據樣本持續時問為1h，采樣頻率為25.6Hz，同時系統還獲取了相應的每小時平均風速。本文即利用這些橋面加速度數據驗證本文所提改進EWT模態參數識別方法的可行性。

根據文獻[21]的有限元分析結果可知，汀九斜拉橋的前8階自振頻率介于0.1Hz至0.5Hz之問，為降低計算成本并獲得更精確的模態參數識別結果，對數據進行了重采樣處理，處理后的數據采樣頻率降為2.56Hz，同時采用截止頻率為0.5Hz的8階Cheby-shev I型低通濾波器對數據進行濾波處理。圖16給出了臺風York 2激勵下，基于Burg算法計算得到的橋面24個測點加速度數據的功率譜。從圖16可以看出，各階自振頻率峰值比較明顯，適合用于劃分頻帶。以7號測點數據分析為例，圖17給出了基于EWT分解所得結構前3階模態響應后，應用RDT技術得到的隨機減量指紋信號。圖18給出了這些隨機減量指紋的對數幅值曲線和相位曲線。分別對表2所列4種臺風工況下的數據，采用本文所提改進EWT的模態參數識別方法，基于24個測點數據識別得到結構的各階自振頻率和阻尼比，然后對識別結果進行算術平均，得到汀九斜拉橋前8階自振頻率和阻尼比，如表3所示。為了比較，表3中還給出了文獻[22]基于隨機子空問方法（SSI-DATA）的前8階自振頻率和阻尼比識別結果。從表3可以看出，本文方法與SSI-DATA方法的頻率識別結果基本一致，識別的阻尼比大部分在1%-3%范圍內，與實際情況吻合。本文所提方法簡單易操作，且能快速精確地識別出結構的低階頻率和阻尼比。

4結論

本文提出了基于改進經驗小波變換的土木工程結構模態參數識別方法，典型數值模擬信號、ASCEBenchmark數值模型和臺風激勵下香港汀九斜拉橋的模態參數識別結果驗證了方法的正確性、有效性和適用性。本文的主要結論包括：

（1）針對EWT方法識別噪聲信號模態參數時，由于傅里葉頻譜易受噪聲影響而頻率邊界估計準確性差的問題，提出了采用基于Burg算法的自回歸功率譜替代傅里葉頻譜的信號頻帶劃分技術，可更準確地估計信號頻帶邊界;

（2）基于自回歸功率譜劃分的頻帶，采用EWT方法構建的小波濾波器組，可很好地分離結構各階模態響應，結合基于Hilbert變換的單分量模態參數識別方法，準確識別了典型數值模擬信號和ASCE Benchmark數值模型的自振頻率和阻尼比，且識別精度高于基于小波變換的方法;結合隨機減量技術，有效地識別了臺風激勵下香港汀九斜拉橋的前8階自振頻率和阻尼比。