幾種多態含能材料構型轉變的DFT研究

姚如意，張樹海，茍瑞君，李連強

(1.中北大學環境與安全工程學院，山西 太原 030051；2.兵器工業衛生研究所，陜西 西安 710065)

引 言

多態含能材料晶型轉變的研究對炸藥的爆轟性能和安全性具有重要意義。對幾種多態含能材料在熔態TNT和DNP中的溶解性研究表明[1]，RDX、HMX及CL-20在熔態TNT中的溶解度分別為3.47g /100g、0.24g /100g和5.78g /100g，在熔態DNP中的溶解度分別為12.28g /100g、2.64g /100g和7.02g /100g 。而一旦高能固相炸藥在熔鑄炸藥載體中能溶解，則高能固相炸藥在熔態的熔鑄炸藥載體中就可能會隨著溫度的變化溶解結晶，此過程還有可能造成多態含能材料晶型的轉變。在對幾種多態含能材料在熔態TNT和DNP中的溶解性及其結晶晶型的研究中發現[1]，CL-20在TNT、DNP中溶解后回收的晶型均由ε型變為β型。彈藥中炸藥發生相變時，其密度、感度、熱穩定性等就會隨之發生變化，導致晶體體積發生膨脹或收縮，在晶體內部形成內應力和損傷缺陷，成為潛在的熱點和剪切帶，影響武器彈藥的使用和貯存[2]。因此多態含能材料晶型轉變的研究對于熔鑄炸藥生產、貯存、運輸和使用過程的穩定性及其相應的武器彈藥安全性、可靠性研究均有重要意義[3]。

多態含能材料晶型轉變的研究多為針對始態和末態穩定存在的晶型在熱力學和動力學角度進行計算和解釋，對多態含能材料構型轉變的路徑進行的計算卻很少。Mrinal Ghosh等[4]采用QST2的方法計算了β-RDX→α-RDX、γ-HMX→β-HMX、ε-CL-20→β-CL-20構型轉變過程。本研究采用TS方法，搜尋了β-RDX→α-RDX、γ-HMX→β-HMX、ε-CL-20→β-CL-20及β-FOX-7→α-FOX-7分子構型轉變過程中的過渡態結構，確定它們的轉變路徑，通過研究分子構型的轉變過程在一定程度上可以大致反映出晶型在轉變過程中分子構型變化的一個基本情況。并通過計算吉布斯自由能隨構型轉變過程的變化，分析多態含能材料分子構型轉變的難易順序。

1 理論計算

1.1 過渡態搜尋

1.1.1 計算環境

多態含能材料在溶劑中之所以容易發生晶型轉變，與溶劑分子和多態含能材料分子間作用力分不開。為了更有效地對多態含能材料的構型變化進行分析，本研究在溶劑丙酮中對不同分子構型間的過渡態結構進行搜尋，為了更好地表現溶劑的平均效應，計算時采用隱式溶劑環境。

1.1.2 計算方法

借助Gaussian 09[5]軟件，運用密度泛函理論(DFT)，首先在密度泛函B3LYP方法和基組6-31G*下于隱式溶劑丙酮中對β-RDX與α-RDX[6-7]、γ-HMX與β-HMX[8-9]、ε-CL-20與β-CL-20[10]、α-FOX-7與β-FOX-7[11]進行結構優化；然后進行勢能面柔性掃描，快速確定過渡態結構在勢能面上的大致位置區間，初猜過渡態的結構；在B3LYP/6-311+G(D，P)及MO62X/6-311+G(D，P)方法和基組下，選用LTS算法，對β-RDX→α-RDX、γ-HMX→β-HMX、ε-CL-20→β-CL-20和β-FOX-7→α-FOX-7構型間的過渡態構型進行優化，直至頻率分析中有且僅有一個虛頻，此時初步確定是反應的過渡態結構；通過IRC計算，對過渡態結構進行驗證，通過此方法搜尋出分子構型在轉變過程中的所有過渡態結構。圖1為優化后的α-RDX、β-RDX、β-HMX、γ-HMX、β-CL-20、ε-CL-20、β-FOX-7和α-FOX-7的分子構型圖。

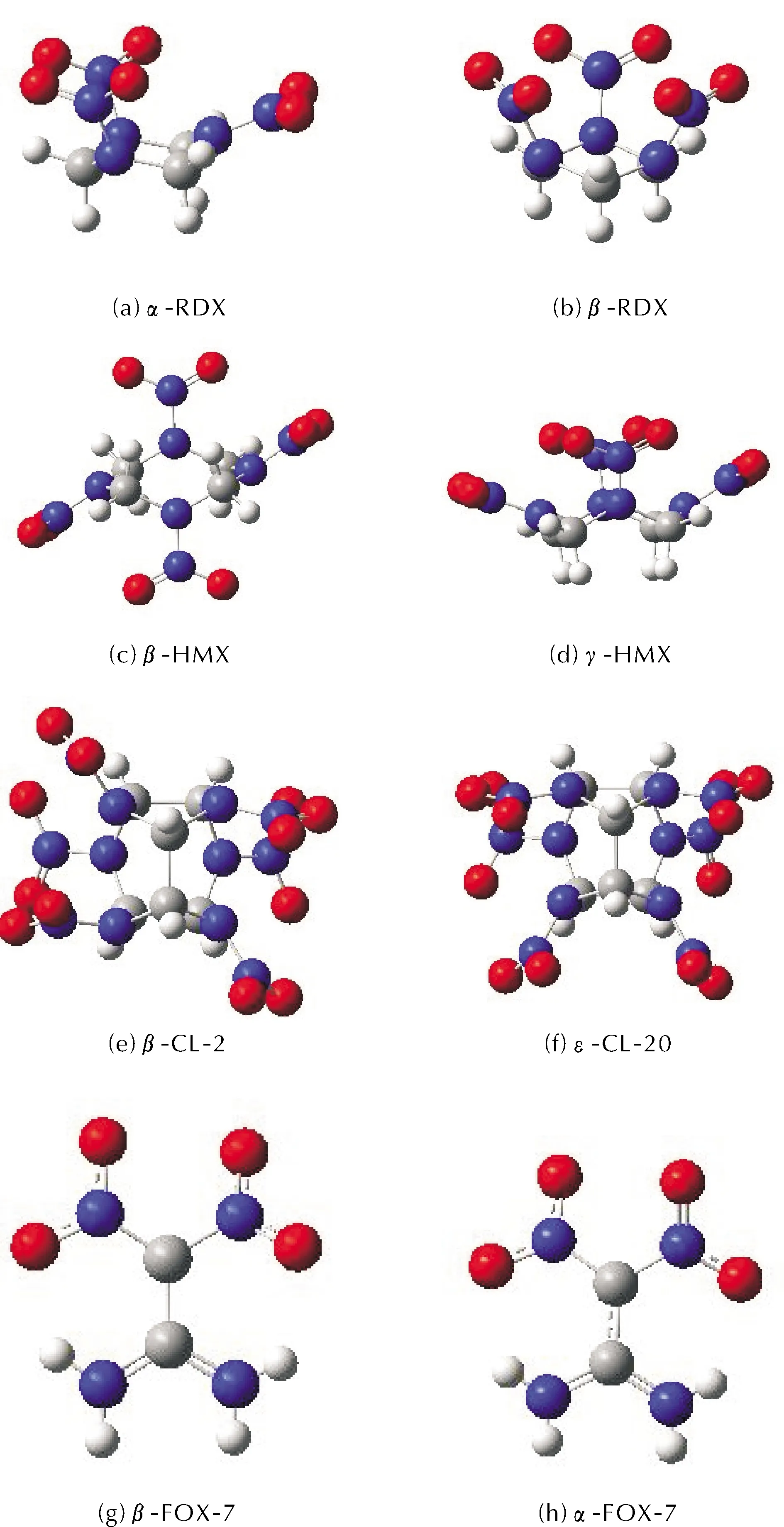
圖1 分子構型圖

1.2 吉布斯自由能計算

借助Gaussian 09軟件，首先在B3LYP/6-311+G(D，P)的方法和基組下對α-RDX與β-RDX、β-HMX與γ-HMX、ε-CL-20與β-CL-20、α-FOX-7與β-FOX-7及它們各自的過渡態結構氣相環境下進行優化，繼續在B63LYP/6-311+G(D，P)的方法和基組下進行熱力學參數計算，然后將得到的熱力學校正量加到PWPB95-D3/def2-QZVP方法下計算的電子能量(E)上。B3LYP/6-311+G(D，P)方法和基組下的零點能(ZPE)、焓(ΔH)和熵(S)的校正因子[12]為0.9887、1.0102、1.0161，吉布斯自由能計算公式為G=E+ZPE+ΔH-TS。

2 結果與討論

2.1 β-RDX→α-RDX的分子構型轉變路徑

2.1.1 TS計算

通過觀察對比圖1(a)和圖1(b)，分析由β-RDX到α-RDX，主要是有一個硝基發生了偏轉，在B3LYP/6-311+G(D，P)下對此鍵角進行勢能面柔性掃描，借助Gview在β-RDX的基礎上對其中一個硝基的角度不斷調節作為過渡態的初猜結構，然后進行TS計算，直至出現唯一的虛頻-53.05cm-1，此過渡態結構記為TS1。

2.1.2 IRC驗證

對這一過渡態結構繼續在相同的方法和基組B3LYP/6-311+G(D，P)下進行IRC計算，從計算結果分析TS1處于勢能面的能量最高點，從最高點開始分別向曲線兩側趨向β-RDX和α-RDX結構，因此確定TS1即為β-RDX→α-RDX構型轉變過程的過渡態結構。

2.1.3 轉變過程

β-RDX→α-RDX的構型轉變過程如圖2所示。

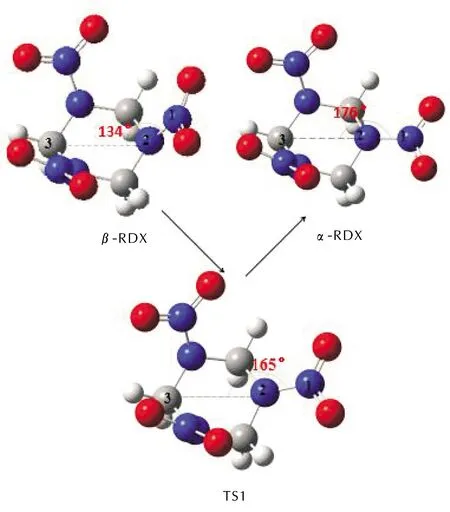
圖2 β-RDX→α-RDX的分子構型轉變過程

由圖2可知，β-RDX→α-RDX的構型轉變過程為β-RDX→TS1→α-RDX。

2.1.4 吉布斯自由能

對β-RDX、TS1和α-RDX的電子能量(E)、零點能(ZPE)、焓(ΔH)、熵(S)和吉布斯自由能進行計算。β-RDX→α-RDX分子構型轉變過程中的吉布斯自由能走勢如圖3所示。

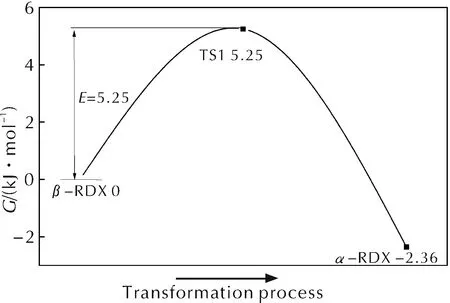
圖3 β-RDX→α-RDX分子構型轉變過程中的吉布斯自由能走勢

由圖3可以看出，β-RDX→α-RDX分子構型轉變時首先需要經過渡態結構TS1，這個轉變需要克服的自由能能壘為5.25kJ/mol。

2.2 γ-HMX→β-HMX的分子構型轉變路徑

2.2.1 TS計算

通過觀察對比圖1(c)和圖1(d)，分析γ-HMX和β-HMX之間主要是有兩個硝基發生了偏轉，猜測由γ-HMX→β-HMX的分子構型轉變過程中可能不止一個過渡態結構。在M062X/6-31G*計算水平下，對這兩個鍵角分別進行了勢能面柔性掃描；借助Gview軟件，在γ-HMX的基礎上首先分別對這兩個硝基的角度進行調節來作為過渡態結構的初猜；然后進行TS計算，直至頻率分析中出現唯一的虛頻；對這兩個硝基的鍵角分別初猜結束后，再在現有的過渡態結構基礎上改變另一個硝基的鍵角來作為下一個過渡態搜尋的初猜，直至TS計算后頻率分析中有且僅有一個虛頻，以此方法不斷搜尋所有可能的過渡態結構。最終確定HMX兩種分子構型間有3個過渡態結構TS1、TS2和TS3，虛頻分別為-81.20、-59.52和-59.41cm-1。

2.2.2 IRC驗證

對所有的過渡態結構在同樣的方法和基組M062X/6-31G*下進行IRC計算，發現TS1、TS2和TS3的IRC能量曲線中能量最高點正是對應的過渡態結構TS1、TS2和TS3，且TS1的IRC能量曲線中趨于平緩的曲線兩側分別指向γ-HMX與TS2的方向，TS2的IRC能量曲線中趨于平緩的曲線兩側分別指向TS1與TS3，TS3的IRC能量曲線中趨于平緩的曲線兩側分別指向TS2與β-HMX的方向，以此驗證TS1、TS2和TS3確實是γ-HMX→β-HMX分子構型轉變過程中的過渡態結構。

2.2.3 轉變過程

γ-HMX→β-HMX的分子構型轉變過程如圖4所示。

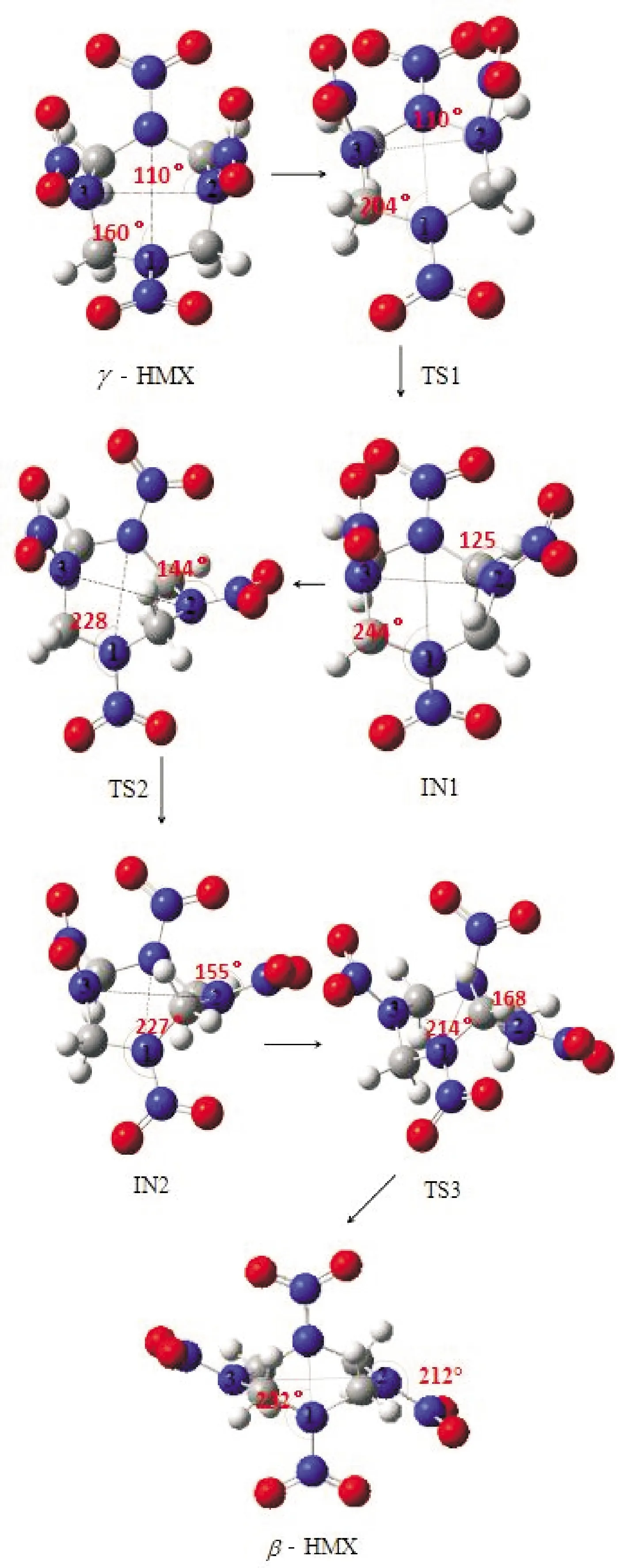
圖4 γ-HMX→β-HMX的分子構型轉變過程

由圖4可知，γ-HMX→β-HMX的構型轉變過程為γ-HMX→TS1→IN1→TS2→IN2 →TS3→β-HMX。

2.2.4 吉布斯自由能

對γ-HMX、TS1、IN1、TS2、IN2、TS3和β-HMX的電子能量(E)、零點能(ZPE)、焓(ΔH)、熵(S)和吉布斯自由能進行計算。γ-HMX→β-HMX分子構型轉變過程中的吉布斯自由能走勢圖如圖5所示。

由圖5可以看出，γ-HMX→β-HMX的分子構型轉變不是一步完成的，γ-HMX先形成自由能比其低的IN1結構，中間經過TS1結構，由γ-HMX到IN1需要的自由能能壘為22.21kJ/mol，接著IN1又變成比其自由能更低的IN2，由IN1越過TS2需要克服的自由能能壘為4.68kJ/mol，最后才由IN2越過TS3，克服5.93kJ/mol的自由能能壘轉變成β-HMX。這一轉變過程與Ostwald規則[13]剛好相符。

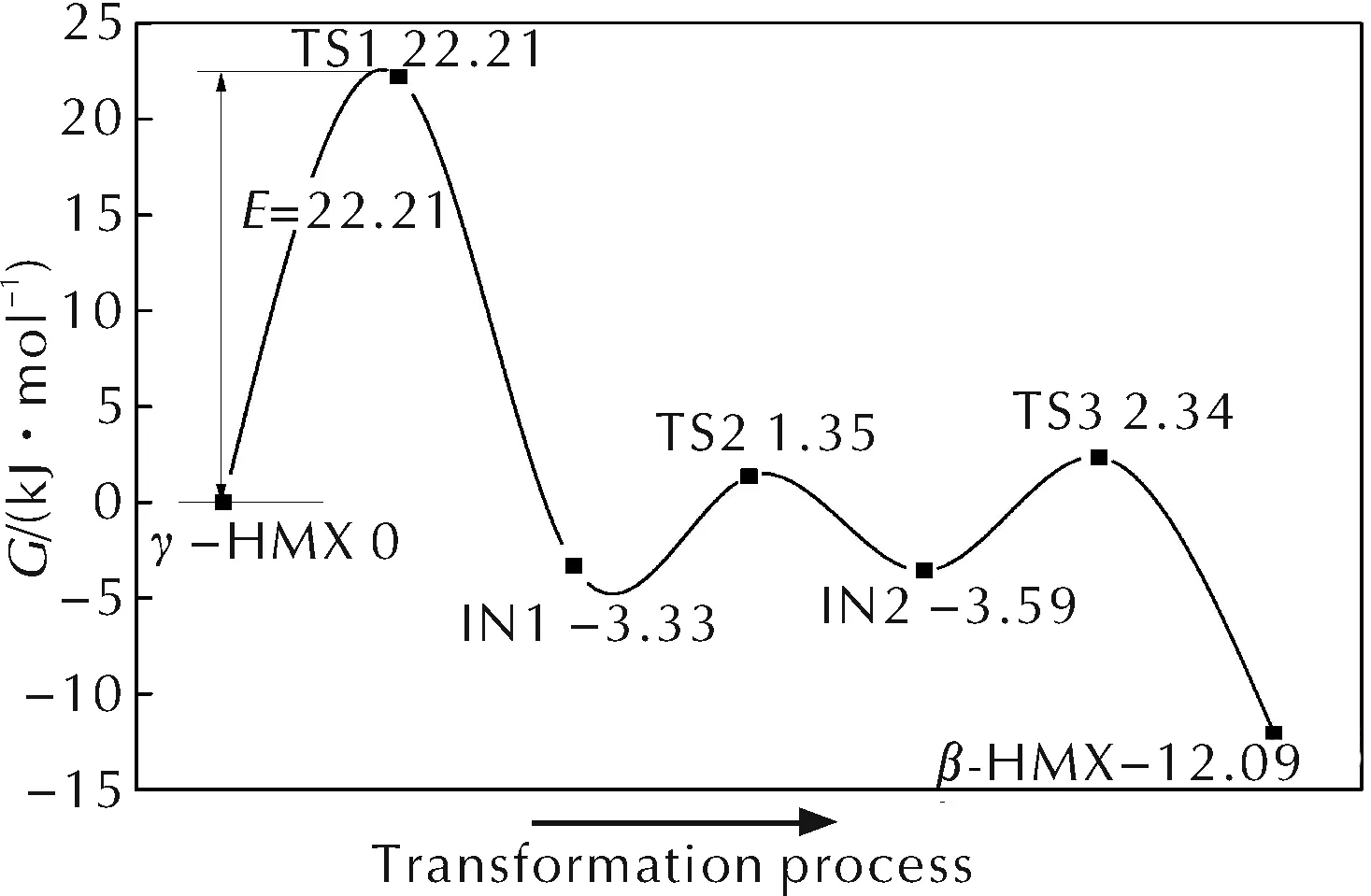
圖5 γ-HMX→β-HMX分子構型轉變過程中的吉布斯自由能走勢

2.3 ε-CL-20→β-CL-20的分子構型轉變路徑

2.3.1 TS計算

通過觀察對比圖1(e)和圖1(f)，初步分析ε-CL-20和β-CL-20之間主要是有兩個硝基發生了偏轉，猜測在ε-CL-20→β-CL-20的分子構型轉變過程中不只一個過渡態結構。在密度泛函B3LYP和基組6-311+G(D，P)下，對這兩個鍵角分別進行了勢能面柔性掃描；借助Gview軟件，在ε-CL-20的基礎上分別先對這兩個硝基的角度進行調節來作為過渡態的初猜結構；然后進行TS計算，直至出現唯一的虛頻；再在現有的過渡態結構的基礎上改變另一個硝基的鍵角來作為下一個過渡態結構搜尋的初猜，直至TS計算后頻率分析中有且僅有一個虛頻，以此方法不斷搜尋所有的過渡態結構。最終確定ε-CL-20→β-CL-20分子構型轉變過程中的過渡態結構為TS1和TS2，虛頻分別為-48.55和-53.43cm-1。

2.3.2 IRC驗證

在B3LYP/6-311+G(D，P)下對TS1和TS2進行IRC驗證，發現TS1和TS2的IRC能量曲線中能量最高點正是對應的過渡態結構TS1和TS2，且TS1的IRC能量曲線中趨于平緩的曲線兩側分別指向ε-CL-20與TS2的方向，TS2的IRC能量曲線中趨于平緩的曲線兩側分別指向TS1與β-CL-20的方向，以此驗證TS1和TS2確實是ε-CL-20→β-CL-20分子構型轉變過程中的過渡態結構。

2.3.3 轉變過程

ε-CL-20→β-CL-20的分子構型轉變過程如圖6所示。由圖6可知，ε-CL-20→β-CL-20的構型轉變過程為ε-CL-20→TS1→IN1→TS2→β-CL-20。

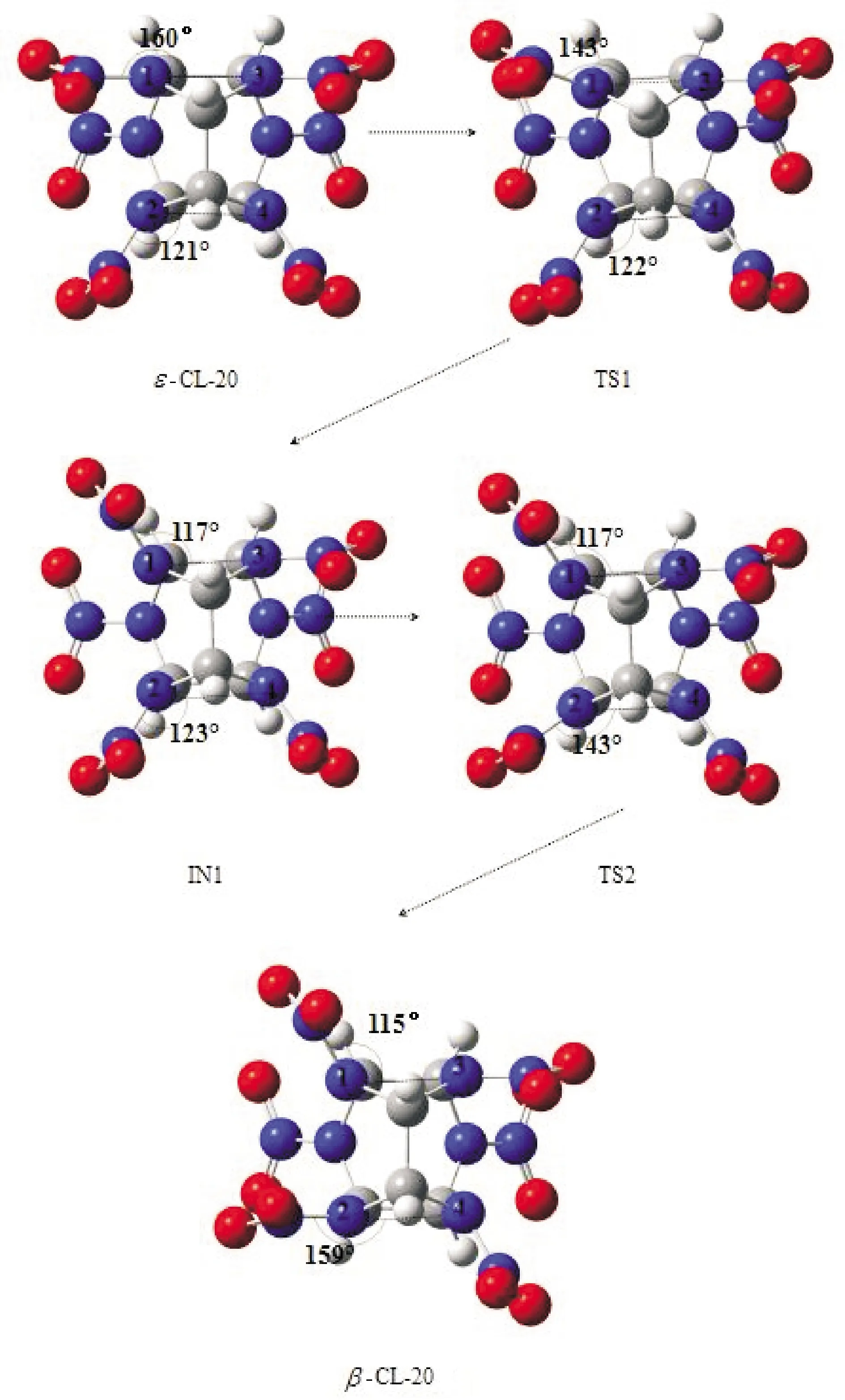
圖6 ε-CL-20→β-CL-20的分子構型轉變過程

2.3.4 吉布斯自由能

對ε-CL-20、TS1、IN1、TS2和β-CL-20的電子能量(E)、零點能(ZPE)、焓(ΔH)、熵(S)和吉布斯自由能進行計算。ε-CL-20→β-CL-20分子構型轉變過程中的吉布斯自由能走勢如圖7所示。

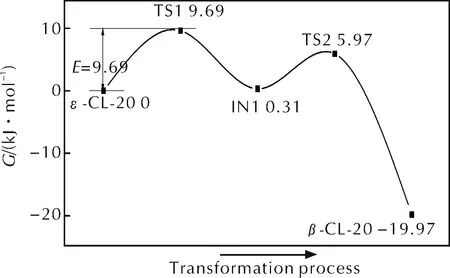
圖7 ε-CL-20→β-CL-20分子構型轉變過程中的吉布斯自由能走勢

由圖7可知，ε-CL-20→β-CL-20的分子構型轉變不是一步完成的，ε-CL-20先越過TS1，克服自由能能壘9.69kJ/mol變成IN1，最后IN1才越過TS2變成ε-CL-20，由IN1轉變為TS2需要克服的自由能能壘為6.28kJ/mol。

2.4 β-FOX-7→α-FOX-7的分子構型轉變路徑

2.4.1 TS計算

通過觀察對比圖1(g)和圖1(h)，初步分析β-FOX-7和α-FOX-7之間的差異主要表現在兩對二面角上，在B3LYP/6-311+G(D，P)方法和基組下，對這兩個鍵角分別進行了勢能面柔性掃描；借助Gview軟件，在β-FOX-7的基礎上首先分別對這兩個硝基的角度進行調節來作為過渡態結構的初猜；然后進行TS計算，直至頻率分析中出現唯一的虛頻；再在現有的過渡態結構的基礎上改變另一個硝基的鍵角來作為下一個過渡態搜尋的初猜，接著進行TS計算。最終確定由β-FOX-7→α-FOX-7分子構型轉變過程中有一個過渡態結構TS1，虛頻為-101.27cm-1。

2.4.2 IRC驗證

在B3LYP/6-311+G(D，P)下對TS1進行IRC驗證，IRC能量曲線中能量最高點正是對應的過渡態結構TS1，且TS1的IRC能量曲線中趨于平緩的曲線兩側分別指向β-FOX-7與α-FOX-7的方向，以此驗證TS1確實是β-FOX-7→α-FOX-7分子構型轉變過程中的過渡態結構。

2.4.3 轉變過程

β-FOX-7→α-FOX-7的分子構型轉變過程如圖8所示。

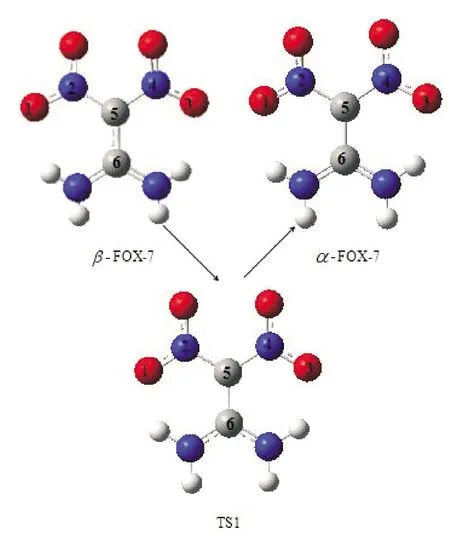
圖8 β-FOX-7→α-FOX-7的分子構型轉變過程

由圖8可知，在β-FOX-7→TS1→α-FOX-7的分子構型轉變過程中，原子1-2-5-6所在的二面角變化為21°→-6°→-34°，原子3-4-5-6所在的二面角變化為21°→7°→-6°。β-FOX→α-FOX的構型轉變過程為β-FOX→TS1→α-FOX。

2.4.4 吉布斯自由能

對β-FOX-7、TS1和α-FOX-7的電子能量(E)、零點能(ZPE)、焓(ΔH)、熵(S)和吉布斯自由能進行計算。β-FOX-7→α-FOX-7分子構型轉變過程中的吉布斯自由能走勢如圖9所示。

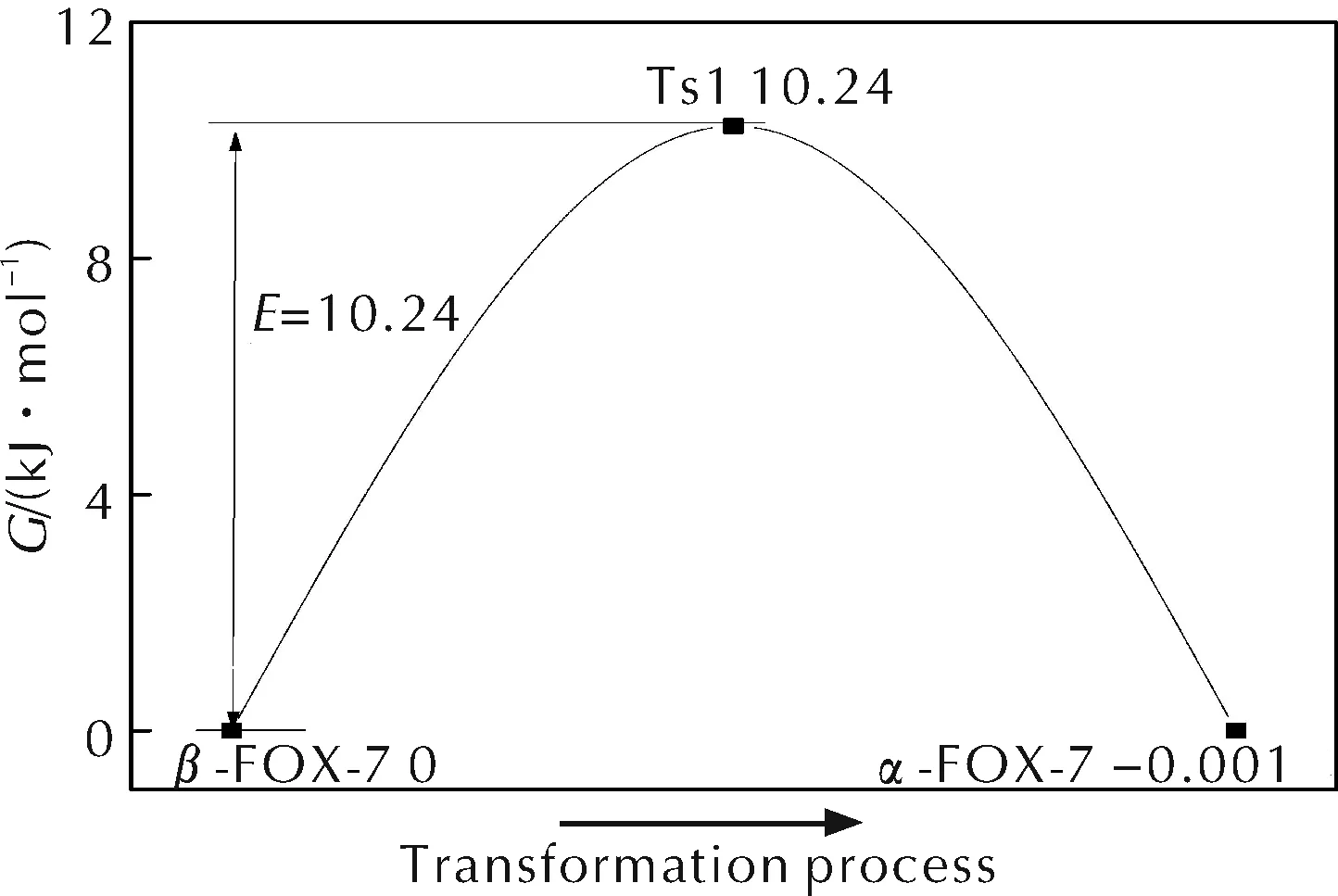
圖9 β-FOX-7→α-FOX-7分子構型轉變過程中的吉布斯自由能走勢

由圖9可以看出，由β-FOX-7到α-FOX-7需要越過的自由能能壘為10.24kJ/mol。

3 結 論

(1)β-RDX→α-RDX、γ-HMX→β-HMX、ε-CL-20→β-CL-20和β-FOX-7→α-FOX-7的分子構型轉變過程分別為β-RDX→TS1→α-RDX、γ-HMX→TS1→IN1→TS2→IN2→TS3→β-HMX、ε-CL-20→TS1→IN1→TS2→β-CL-20和β-FOX-7→TS1→α-FOX-7。由這幾種多態含能材料分子構型轉變過程可知，分子構型轉變并非一步完成的。

(2)多態含能材料分子構型間的轉變，首先會由亞穩構型越過過渡態結構，然后才會進一步向亞穩結構轉變。β-RDX→α-RDX、γ-HMX→β-HMX、ε-CL-20→β-CL-20和β-FOX-7→α-FOX-7需要克服的自由能能壘分別為5.25、22.21、9.69和10.24kJ/mol，轉變的難度大小排序為：HMX? FOX-7>CL-20>RDX。