函數極限求值的若干方法探究

陳書坤

(山東青年政治學院 信息工程學院，濟南 250103)

關于函數極限的求解方法，在高等數學教材中主要介紹了極限的四則運算、兩個重要極限、等價無窮小代換、洛必達法則，等等。為了豐富求函數的極限方法，現總結介紹幾種高等數學教材中不常用的函數極限求解方法。

1 利用微分中值定理求極限

在利用微分中值定理時需要構造適當的函數，而函數可以通過觀察極限的結構來進行合理構造。

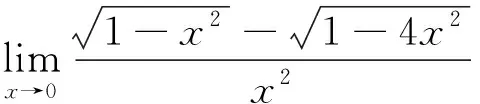
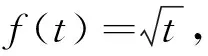
其中ξ∈(1-4x2,1-x2)。當x→0時，ξ=1

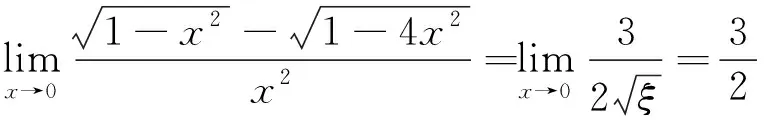
(說明：本題也可用洛必達法則或泰勒展開公式求解。)

2 利用泰勒展開公式求極限

在求解函數極限時有時需要用到泰勒展開公式，尤其是一些初等函數的麥克勞林公式，如ex、sinx、cosx、ln(1+x)、(1+x)α等。在使用泰勒公式時，至于需要將所展函數展開到第幾項還需要根據具體情況進行相應處理。例如，若求解的是分式函數的極限，則需要根據分子、分母的冪次來決定，原則是展開后(去掉高階無窮小)使得分子、分母的最高次冪相等。

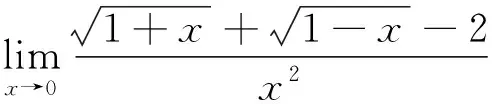
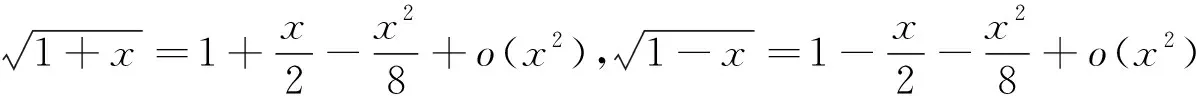
所以原式

(說明：本題也可用洛必達法則求解，但由于本題分子中含有根號，求導時會變得較為繁瑣，而使用泰勒展開公式會更簡便。)

3 利用積分中值定理求極限

利用積分中值定理可以求某些含有定積分表達式的函數極限。

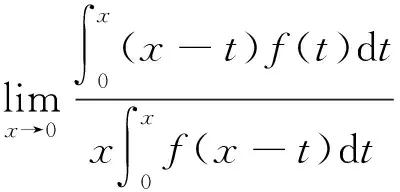
解：由于f(x)在x=0的某鄰域內連續，則由積分中值定理可知：

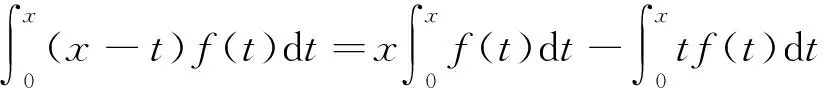
則有：

(說明：本題從結構上來看可以使用洛必達法則求解，但在求解時遇到了不符合洛必達法則條件的情況，因此不能使用洛必達法則。)

4 利用導數的定義求極限

當在函數極限出現有關函數導數的相關條件時，可以考慮根據導數的定義表達式進行求解。

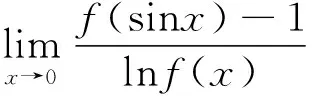
解：由題知

(說明：本題也可以利用洛必達法則和拉格朗日中值定理求解。)

5 利用函數的冪級數展開式求極限

當所求函數極限中出現諸如ex、sinx、cosx、ln(1+x)等類似形式的函數時，可以考慮將其展開為冪級數。該方法可以將復雜函數表示為簡單的冪級數，從而便于求出函數極限。

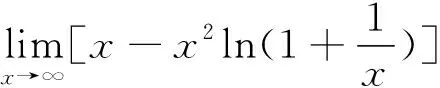
(說明：該題也可以通過換元將其變為分式函數，然后使用洛必達法則求解。)

6 利用函數與極限的關系求極限

有些函數的求極限問題可以根據函數與極限的關系進行求解：若limf(x)=A，當且僅當f(x)=A+α(x)，α(x)→0

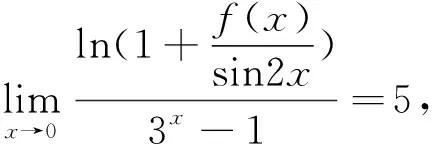
于是f(x)=sin2x·[e(5+α(x))·(3x-1)-1]

而e(5+α(x))·(3x-1)-1～(5+α(x))·(3x-1)(x→0)

則有：

(說明：本題也可以直接根據四則運算法則及等價無窮小代換求解。)