基于多目標粒子群算法的機器人逆運動學求解方法

劉洋

（四川大學計算機學院，成都 610065）

0 引言

已知機器人末端執行器的位置姿態信息，求解機器人各關節角度值的過程稱為機器人的逆運動學求解。機器人逆運動學是機器人領域的基礎問題，在工程實踐中有著十分廣泛的應用需求。

機器人逆運動學的求解方法很多，主要可以分為解析方法和數值方法兩類。由于解析方法[1]具有很大的局限性且對自由度較高的機器人效果不佳，目前主流的研究工作均集中在數值方法上。數值方法的本質就是將機器人逆運動學問題轉換成一個優化問題，再利用相關優化方法進行求解。目前應用較多的數值方法主要分為神經網絡和群體智能方法兩類。通過神經網絡的方法[2]，可以很好地實現對機器人的逆運動學求解。但是神經網絡精度的高低完全取決于所使用訓練集質量的好壞，而不同結構的機器人之間無法共享同一訓練集；因此必須針對特定的機器人結構單獨提取高質量的訓練集，這無疑大幅增加了神經網絡方法的使用成本。相比于神經網絡方法，群體智能方法在通用性上有著巨大的優勢。常用的群體智能方法，如粒子群算法[3]、螢火蟲算法[4]、遺傳算法[5]等，在機器人逆運動學求解中均取得了不錯的效果，實現了很高的位置精度。但在工程實踐中，很多應用場景對姿態精度也有很高的要求，上述的單目標優化方法無法同時解決這兩方面的需求。

針對機器人逆運動學求解中對位置精度和姿態精度兩方面的需求，文章將其轉化為多目標優化問題，并通過多目標粒子群算法加以實現。

1 機器人逆運動學

1.1 機器人運動學模型

以自由度為6的機器人為例，根據D-H方法[6]建立機器人各關節坐標系Oxiyizi，如圖1所示。Ox0y0z0

表示世界坐標系，Ox6y6z6表示工具坐標系。如何構建起兩個坐標系之間的轉換關系正是機器人運動學研究的內容。

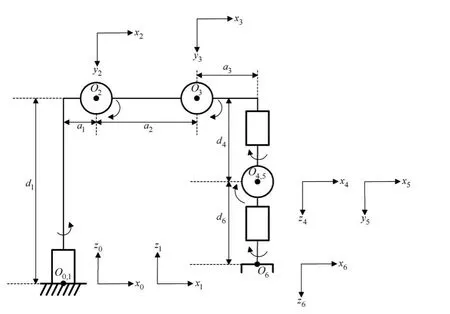
圖1 機器人關節坐標系

其中，p=[px,py,pz]T表示機器人工具坐標系的原點在世界坐標系中的坐標，即機器人末端控制器的位置信息；[n,s,a]表示機器人工具坐標系各坐標軸單位向量在世界坐標系中的坐標，即機器人末端控制器的姿態信息，用歐拉角形式表示為

1.2 機器人逆運動學求解

相比于正運動學求解，機器人逆運動學求解過程無疑要困難很多。在已知機器人各關節角度值的情況下，可以利用公式（1）求解出末端執行器的位置和姿態信息：

其中，p、e為機器人末端執行器的位置和姿態信息；Fposition()、Forientation()表示運用機器人正運動學模型對機器人末端執行器的位置和姿態信息進行求解的過程。

利用公式（2），可以將機器人逆運動學表述為多目標優化問題：

其中，ptar、etar為機器人末端控制器的目標位置和姿態；qtar為待求解的機器人關節轉角值；qinit為機器人關節轉角初始值為機器人關節轉角θi的限制范圍。

公式（3）表明逆運動學求解需要滿足三方面的目標要求，即位置精度最高、姿態精度最高以及關節角度值變化最小。針對這一多目標優化問題，文章根據位置精度和姿態精度的目標函數構造相應的適應度函數并采用多目標粒子群算法[7]進行求解；在此基礎之上，利用關節角度值變化的目標函數對所得的解集進行多解優化，從而完成機器人逆運動學的求解。

2 多目標粒子群算法

2.1 基本定義

由于多個適應度函數的存在，在多目標粒子群算法中需要引入帕累托支配的概念：對于向量u=[u1,u2,…,un] 和v=[v1,v2,…,vn]，當且僅當u部分小于v時，u支配v。即：

當兩組適應度之間存在帕累托支配關系時，可以根據支配關系進行比較評價優劣。但很多時候兩組適應度之間并不存在帕累托支配關系，無法比較評價優劣，此時兩組解均應當進行保留。因此，將所有相互之間沒有支配關系的解構成一個集合，即帕累托最優解集：

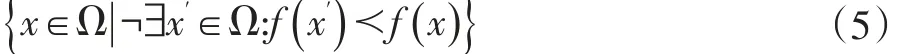
2.2 算法流程

多目標粒子群算法中的基本搜索單位是粒子，具有位置和速度兩種屬性。在逆運動學求解過程中，每個粒子的位置都是一組關節角度值，表示逆運動學問題的一組可能解；每個粒子的速度表示該粒子在空間內搜索時的方向和幅度，并隨著搜索的進行不斷進行調整。

針對逆運動學問題的多目標粒子群優化算法流程如圖2所示。

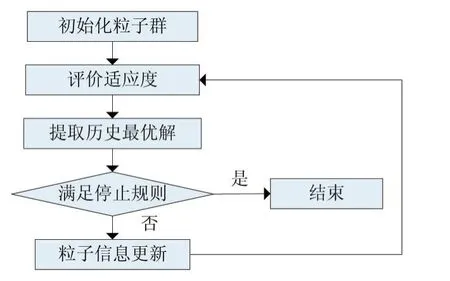
圖2 算法流程圖

粒子群初始化：粒子群初始化主要包括粒子位置和速度的初始化。粒子位置的初始化通過在各關節角度限制范圍內隨機生成來實現。粒子速度的初始化通過在各關節搜索速度范圍內隨機生成來實現。

適應度計算：根據公式（2）計算粒子位置代表的關節角度值對應的末端執行器位置姿態。根據所得的末端執行器位置姿態分別計算粒子對應的多個適應度函數的值，從而完成對粒子適應度的計算。

歷史最優解提取：包括帕累托最優解集的更新、粒子的局部最優解Pd的更新以及粒子群的全局最優解Pg的更新。局部最優解Pd的更新根據帕累托支配關系即可確定。帕累托最優解集的更新也通過帕累托支配關系判定，同時要盡可能的保持解集中解的多樣性。全局最優解Pg的更新則需要在帕累托最優解集更新完成的基礎上進行。

粒子信息更新：當全局最優解Pg不滿足精度要求并且迭代次數沒達到上限時，需要對粒子的位置和速度信息進行更新，從而開始新一輪的迭代：

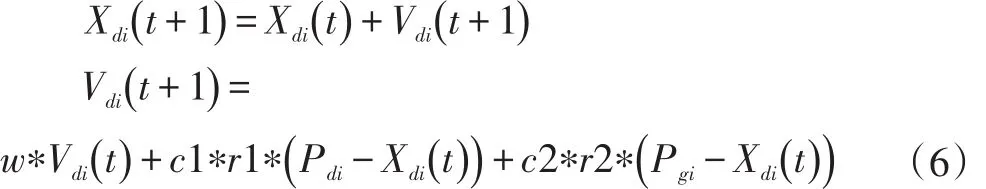
多解優化：當全局最優解Pg滿足精度要求或者迭代次數達到上限時，算法停止迭代，需要進一步對帕累托最優解集進行多解優化，從帕累托最優解集中選取出最適合的一個作為逆運動學問題的最優解。

2.3 適應度函數的構造

根據公式（3）的描述，需要同時滿足位置、姿態精度最高和關節變化幅度最小三個要求。其中，關節變化幅度最小是在已經實現位置、姿態精度最高基礎上的進一步要求。因此，在帕累托最優解集的優化過程中，僅需要考慮位置精度和姿態精度的適應度函數。

位置精度的適應度函數為：

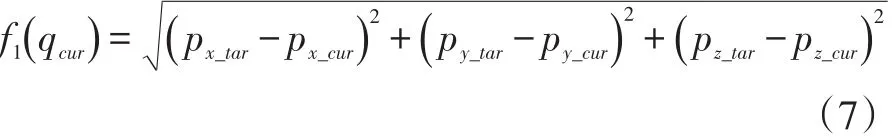
其中，ptar=[px_tar,py_tar,pz_tar]T為目標位置信息；pcur=[px_cur,py_cur,pz_cur]T為通過公式（2）得到的關節轉角qcur對應的實際位置信息。

姿態精度的適應度函數為：

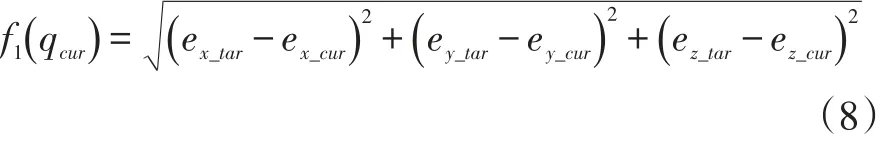
2.4 帕累托最優解集的更新

隨著粒子的不斷搜索，帕勒托最優解集也在不斷進行更新。這一更新通過帕累托支配關系來實現。對于當前解，若其與帕累托最優解集中的解沒有支配或被支配的關系，則將其加入帕勒托最優解集；若其與帕累托最優解集中的解具有支配關系，則將其加入帕累托最優解集并刪除解集中所有被其支配的解；若其與帕勒托最優解集中的解具有被支配關系，則帕累托最優解集保持不變。

隨著迭代次數的增加，帕累托最優解集的規模也在不斷增大。這不僅會對存儲能力提出很高的要求，而且會嚴重影響算法的計算速度。因此，需要對集合中解的數量設定一個上限，并決定帕累托最優解淘汰的策略。文章采用自適應網格方法，將適應度空間按網格等分為許多子空間，并將每個子空間內的解的個數作為該子空間內解的密度值。為了保持解集中解的多樣性，讓集合內的解在空間中分布的更為均勻，選擇密度值最大的子空間內的解隨機進行淘汰。

2.5 歷史最優解的提取

歷史最優解是粒子群算法中的核心參數，包括每個粒子的局部最優解Pd和整個粒子群的全局最優解Pg。它們也需要隨著算法的迭代不斷進行更新。

粒子的局部最優解Pd的更新較為簡單，僅根據帕勒托支配關系即可確定。若當前解支配上一輪迭代的局部最優解，則將當前解確定為局部最優解；若當前解被上一輪迭代的局部最優解支配，則局部最優解保持不變；若二者不存在支配關系，則隨機選擇一個作為局部最優解。

粒子群的全局最優解Pg的更新要從帕累托最優解集中選取。粒子群算法每進行一次迭代，均需要對帕累托最優解集進行更新。在此基礎之上，采用輪盤賭算法選擇一個子空間，子空間被選中的概率與其密度值成反比。選中子空間后，在子空間中隨機選擇一個解作為粒子群的全局最優解Pg進行更新。

2.6 多解優化

經過多目標粒子群算法的搜索，可以得到機器人逆運動學問題的帕累托最優解集。要從中選出唯一的一個作為問題的最優解，需要進行多解優化。由于帕累托最優解集中的解均具有較高的位置精度和姿態精度，在評價體系中添加對關節角度值變化的評價。

多解優化的評價函數為：

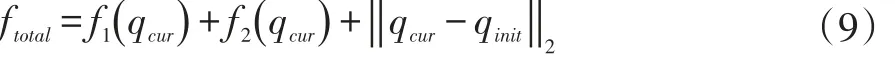
其中，ftotal為多解優化的評價函數。帕累托最優解集中使得ftotal最小的解，即為機器人逆運動學問題的最優解。

3 算法仿真

算法仿真采用的參數如下：粒子數100個、迭代次數 1000次、慣性權重w=0.5、加速常數c1=1.2、c2=1.2。

根據目標位置姿態進行仿真，結果如表2所示。通過多目標粒子群算法的優化，三組目標位置姿態的逆運動學求解均得以實現，且具有很高的位置精度和姿態精度。第三組的實際關節角度與目標關節角度差異很大，這主要是由于機器人逆運動學求解的不唯一性。相比于目標關節角度，求解得到的實際關節角度的關節轉動幅度更小，更符合實際應用的需求。

圖3以第一組目標位置姿態的求解為例，展示了多目標粒子群算法搜索的過程。圖中平面坐標系的坐標軸分別為粒子對應的位置精度和姿態精度的適應度。開始搜索時，由于粒子在搜索空間中隨機均勻的進行搜索，粒子的適應度分布的也較為均勻。隨著迭代次數的增加，粒子在適應度空間內逐漸向原點方向靠攏，粒子搜索的范圍越來越集中；此時的帕累托最優解集的數量很大，這些帕累托最優解共同構成了帕累托前沿，成折線形分布。最終，當迭代完成時，進行搜索的粒子匯聚在一起，幾乎不再運動；帕累托最優解集的數量也大幅減少，且均滿足位置精度和姿態精度的要求。根據多解優化，即可從中選出最優解。

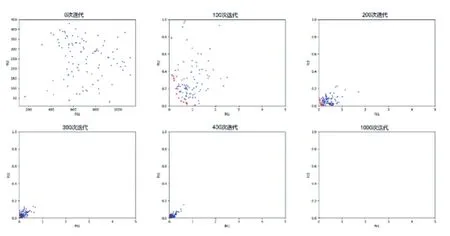
圖3 不同迭代次數的粒子適應度分布圖

表1 目標位置姿態信息表

表2 仿真結果表

4 結語

本文將機器人逆運動學問題轉化為多目標優化問題，并通過多目標粒子群算法進行了實現。在此基礎之上，通過計算機仿真對算法性能進行了測試。仿真測試表明，多目標粒子群算法在同時滿足目標位置精度和姿態精度的情況下，實現了對機器人逆運動學問題的求解。但是多目標粒子群算法對計算能力的要求很高，耗費的時間較長。要實現實時處理，必須采用并行計算且對GPU的性能要求較高。在未來的研究中，可以對算法進行進一步的改進，以提高算法求解速度。