基于EMD的SVR方法在鐵路客流預(yù)測(cè)中的應(yīng)用

孟 歌，王洪業(yè)，李麗輝，韓慧婷

（中國(guó)鐵道科學(xué)研究院集團(tuán)有限公司 電子計(jì)算技術(shù)研究所，北京 100081）

科學(xué)合理地預(yù)測(cè)鐵路客流，能夠有效地輔助運(yùn)營(yíng)管理人員進(jìn)行運(yùn)營(yíng)決策，以便為旅客提供更好的服務(wù)，因此準(zhǔn)確對(duì)客流進(jìn)行預(yù)測(cè)顯得愈發(fā)重要。目前用于客流預(yù)測(cè)的方法主要包括：專(zhuān)家意見(jiàn)法，時(shí)間序列法[1-2]，灰色預(yù)測(cè)法[3-4]，支持向量機(jī)(SVM)[5]，神經(jīng)網(wǎng)絡(luò)[6]等。其中鐵路部門(mén)常用的方法包括BP 神經(jīng)網(wǎng)絡(luò)，支持向量回歸機(jī)(SVR)等方法，均處于前沿地位。BP 神經(jīng)網(wǎng)絡(luò)操作性較好[7]，利于對(duì)大量數(shù)據(jù)進(jìn)行分布式存儲(chǔ)和并行處理，但是收斂速度較慢且容易陷入局部最小值，在原始數(shù)據(jù)量較少且存在噪聲的情況下，預(yù)測(cè)精度往往不夠理想。支持向量回歸機(jī)(SVR)是支持向量機(jī)(SVM)在回歸問(wèn)題上的應(yīng)用模型[8]，它解決了在神經(jīng)網(wǎng)絡(luò)方法中無(wú)法避免的局部極值問(wèn)題，具有在小樣本、非線(xiàn)性環(huán)境下優(yōu)越性較好的特點(diǎn)，因此常采用SVR 方法對(duì)客流進(jìn)行預(yù)測(cè)。

但是由于鐵路客流受多種因素影響，具有高度復(fù)雜性，直接對(duì)客流數(shù)據(jù)進(jìn)行預(yù)測(cè)往往誤差較大，因此本文利用經(jīng)驗(yàn)?zāi)B(tài)分解（EMD ，Empirical Mode Decomposition）方法對(duì)客流進(jìn)行自適應(yīng)的分解，排除噪聲干擾，根據(jù)分解后產(chǎn)生的固有模態(tài)函數(shù)（IMF ，Intrinsic Mode Function）分別進(jìn)行預(yù)測(cè)，建立基于EMD 的SVR 預(yù)測(cè)模型，降低了模型的復(fù)雜度，達(dá)到精確預(yù)測(cè)的目的。

1 基于EMD的SVR模型概述

EMD 適用于處理非線(xiàn)性、非平穩(wěn)數(shù)據(jù)，能夠自適應(yīng)的對(duì)鐵路客流數(shù)據(jù)進(jìn)行高速、有效地分解，具有廣闊的應(yīng)用前景[9]。SVR 方法具有堅(jiān)實(shí)的理論基礎(chǔ)，避開(kāi)了從歸納到演繹的傳統(tǒng)過(guò)程，簡(jiǎn)化了回歸問(wèn)題，在小樣本學(xué)習(xí)領(lǐng)域有極高的效率和準(zhǔn)確率[10]。因此將EMD 方法與SVR 結(jié)合，建立基于EMD 的SVR鐵路客流預(yù)測(cè)模型，對(duì)實(shí)際鐵路客流進(jìn)行預(yù)測(cè)，以期達(dá)到對(duì)日客流進(jìn)行精準(zhǔn)預(yù)測(cè)的目的。

1.1 EMD概述

經(jīng)驗(yàn)?zāi)B(tài)分解(EMD)通過(guò)局部極值的分解方法，能夠?qū)⒎瞧椒€(wěn)、非線(xiàn)性的信號(hào)分解成一系列從高頻到低頻的固有模態(tài)函數(shù)( IMF)，它具良好的完備性，近似正交性，和局部自適應(yīng)性，目前已在網(wǎng)絡(luò)控制、電力、機(jī)械和醫(yī)學(xué)等領(lǐng)域得到了廣泛的應(yīng)用[11-14]，但在鐵路客流預(yù)測(cè)領(lǐng)域中應(yīng)用較少。

鐵路部門(mén)收集到的客流數(shù)據(jù)可以看做一組單位為時(shí)間-人數(shù)的數(shù)據(jù)序列，而EMD 方法的實(shí)質(zhì)是以經(jīng)驗(yàn)為主，通過(guò)客流數(shù)據(jù)的特征時(shí)間尺度，識(shí)別客流數(shù)據(jù)序列中的固有振動(dòng)模態(tài)，然后把它們相應(yīng)地分解出來(lái)。利用EMD 將客流數(shù)據(jù)分解為IMF 需要滿(mǎn)足以下條件：（1） 在整個(gè)數(shù)據(jù)區(qū)段內(nèi)極值點(diǎn)的數(shù)目和過(guò)零點(diǎn)的數(shù)目相差為1 或相等。（2）在任意數(shù)據(jù)點(diǎn)處局部極大值包絡(luò)線(xiàn)和局部極小值包絡(luò)線(xiàn)的平均值為0。

對(duì)于鐵路客流數(shù)據(jù)X(t)，其EMD 方法的具體實(shí)現(xiàn)步驟為：

（1）確定原始客流數(shù)據(jù)X(t)中的所有局部極大值和局部極小值，用三次樣條函數(shù)插值法對(duì)所有的極大值、極小值分別進(jìn)行擬合，進(jìn)而獲得上包絡(luò)線(xiàn)Xmax(t)和下包絡(luò)線(xiàn)Xmin(t)。

（2）求得上包絡(luò)線(xiàn)Xmax(t)和下包絡(luò)線(xiàn)Xmin(t)的均值曲線(xiàn)，獲得平均值m1(t)，公式為：

（3）將平均值m1(t)從原始客流數(shù)據(jù)X(t)中分離出來(lái)，得到第1 個(gè)剩余分量h1(t)，即：

此時(shí)，判斷h1(t)是否滿(mǎn)足IMF 停止條件，滿(mǎn)足即產(chǎn)生第一個(gè)IMF 分量，若不滿(mǎn)足，則將h1(t)看作原始數(shù)據(jù)，重復(fù)j次步驟（1）、（2）、（3），直到得到hj(t)滿(mǎn)足IMF 停止條件，令C1(t)=hj(t)，C1(t)即為分解出來(lái)的第1 個(gè)IMF 分量，記為IMF1。

（4）由于 IMF1 中包含著原始客流數(shù)據(jù)X(t)中頻率最高的部分，將C1(t)從原始客流數(shù)據(jù)X(t)中分離出來(lái)，得到殘差r1：

將r1看作原始數(shù)據(jù)重復(fù)n次步驟（1）～（4），直到最終的殘差rn變成單調(diào)函數(shù)或是常數(shù)為止。

通過(guò)EMD 分解，從原始客流數(shù)據(jù)X(t)中分離出n個(gè)IMF 分量和一個(gè)殘差rn。因此，原始客流數(shù)據(jù)X(t)表達(dá)式為：

1.2 SVR概述

SVR 是近年發(fā)展起來(lái)的性能優(yōu)越的算法，具有良好的泛化能力，其重要理論基礎(chǔ)是統(tǒng)計(jì)學(xué)習(xí)理論。SVR 的基本思想是通過(guò)預(yù)測(cè)誤差最小化來(lái)尋找能較好地接近數(shù)據(jù)點(diǎn)的估計(jì)函數(shù)，通過(guò)非線(xiàn)性映射函數(shù)?:Rn→H將輸入空間的樣本數(shù)據(jù)xi映射到高維特征空間H中，再在此特征空間構(gòu)造最優(yōu)超平面，進(jìn)行線(xiàn)性回歸計(jì)算，從而得到了原來(lái)低維空間里非線(xiàn)性回歸的效果。

設(shè)鐵路客流訓(xùn)練樣本集為(x1,y1)，(x2,y2)，……，(xN,yN)，其中，xi∈Rn，yi∈{-1,1} ，N為客流樣本數(shù)，n為客流特征向量的維數(shù)。

在SVR 中，求最優(yōu)超平面轉(zhuǎn)化為求解二次規(guī)劃問(wèn)題，其中，C為懲罰參數(shù)：

式（1）的對(duì)偶形式為：

利用二次規(guī)劃方法可以得到SVR 的估計(jì)式：

其中，閾值b通過(guò)下式求解：

1.3 基于EMD的SVR模型

通過(guò)EMD 分解，從原始客流數(shù)據(jù)X(t)中分離出n個(gè)IMF 分量和一個(gè)殘差rn。為排除殘差rn的影響，將分離出的n個(gè)IMF 分量作為訓(xùn)練樣本集，通過(guò)SVR 求解得到結(jié)果集。

2 數(shù)值實(shí)驗(yàn)

2.1 樣本選取

本文中以鐵路客票系統(tǒng)中的客流數(shù)據(jù)為依據(jù)，建立基于EMD 的SVR 預(yù)測(cè)模型。以北京西至石家莊的OD 日客流為例，取2017 年6 月1 日—2017 年12 月9 日數(shù)據(jù)作為訓(xùn)練樣本，取2017 年12 月10 日—2017 年12 月27 日數(shù)據(jù)作為測(cè)試樣本進(jìn)行數(shù)值實(shí)驗(yàn)。本文利用MATLAB R2012b 軟件來(lái)實(shí)現(xiàn)數(shù)值檢驗(yàn)，基于EMD 的SVR 預(yù)測(cè)模型參數(shù)選擇方法為人工魚(yú)群算法[15]。

2.2 數(shù)據(jù)預(yù)處理

2.3 實(shí)驗(yàn)及結(jié)果分析

通過(guò)EMD 方法將原始客流數(shù)據(jù)分解，輸入原始客流數(shù)據(jù)后，自適應(yīng)的分解為IMF1 ～I(xiàn)MF6 這6 項(xiàng)分量以及1 項(xiàng)殘差r6。EMD 分解結(jié)果，如圖1 所示。

從圖1 可以看出IMF1 的波動(dòng)頻率最高，IMF2 ～I(xiàn)MF6 逐漸降低，分別分析這6 項(xiàng)IMF 分量與原始客流數(shù)據(jù)的相關(guān)性，利用相關(guān)系數(shù)和P-value 值進(jìn)行檢驗(yàn)，相關(guān)性分析結(jié)果，如表2 所示。

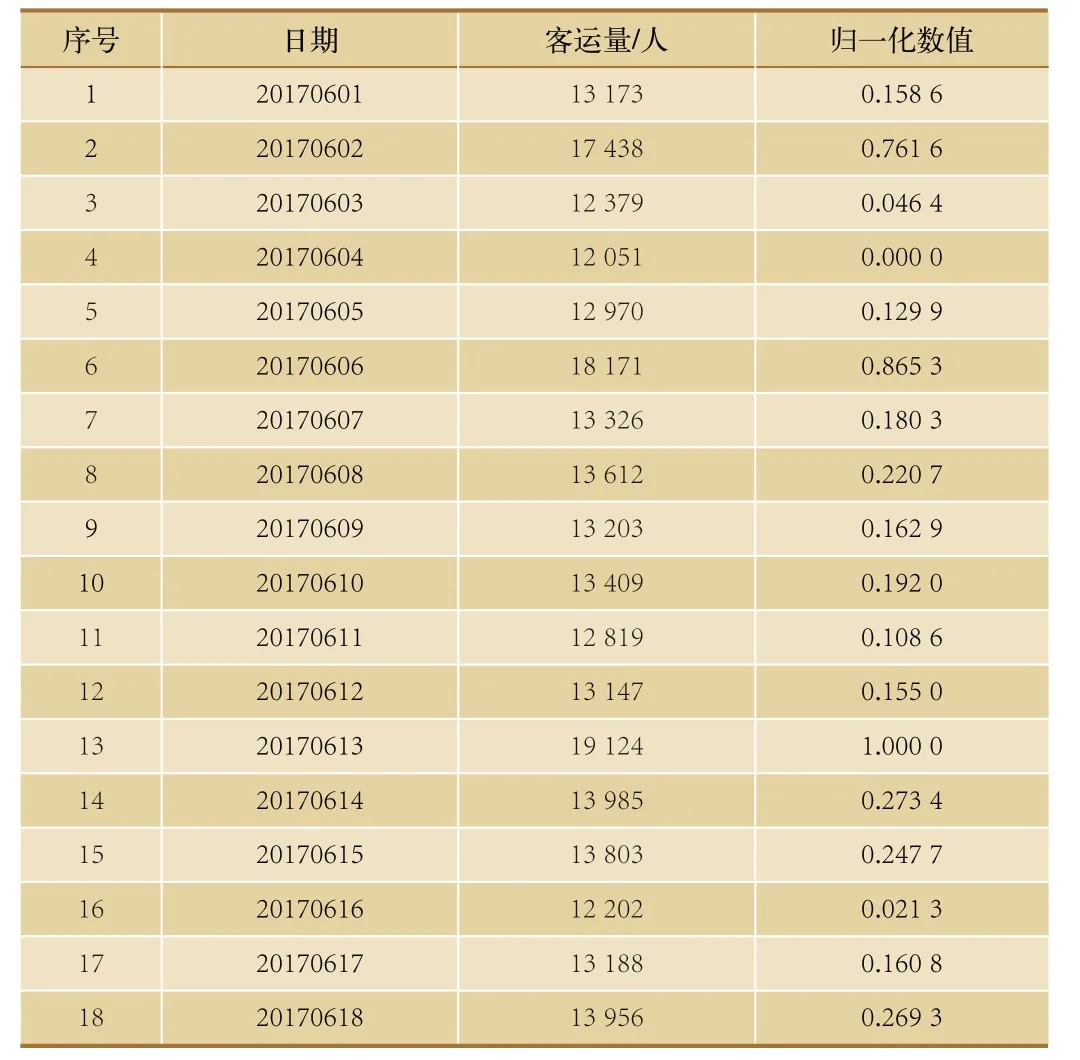
表1 部分原始客流數(shù)據(jù)

從表2 中可以看出殘差r6 的相關(guān)系數(shù)＜0.1，同時(shí)p-value 值遠(yuǎn)＞0.05，而其它IMF 分量的p-value值均＜0.05，證明IMF 分量均與原始客流數(shù)據(jù)相關(guān)性顯著，而殘值r6 與原始數(shù)據(jù)的相關(guān)性不顯著，因此不作為預(yù)測(cè)輸入數(shù)據(jù)處理。將IMF1 ～I(xiàn)MF6 分別作為輸入數(shù)據(jù)進(jìn)行SVR 預(yù)測(cè)，利用魚(yú)群算法優(yōu)化參數(shù)，將預(yù)測(cè)結(jié)果合并后得到最終預(yù)測(cè)結(jié)果，如圖2 所示。為了證明基于EMD 的SVR 優(yōu)于SVR方法，進(jìn)行對(duì)比實(shí)驗(yàn)，采用相同原始客流數(shù)據(jù)進(jìn)行SVR 預(yù)測(cè)，結(jié)果，如圖3 所示。同時(shí)采用相同原始客流數(shù)據(jù)，利用BP 神經(jīng)網(wǎng)絡(luò)方法進(jìn)行預(yù)測(cè)，結(jié)果如圖4 所示。通過(guò)相對(duì)誤差作為評(píng)價(jià)標(biāo)準(zhǔn)，幾種預(yù)測(cè)方法的結(jié)果與原始客流數(shù)據(jù)的相對(duì)誤差、絕對(duì)誤差，如表3、表4 所示。

表2 相關(guān)性分析表

從表3 和表4 中可以看出，基于EMD 的SVR預(yù)測(cè)方法誤差明顯小于SVR 方法和PB 神經(jīng)網(wǎng)絡(luò)方法，其中基于EMD 的SVR 方法平均相對(duì)誤差為13%，而SVR 和PB 神經(jīng)網(wǎng)絡(luò)的平均相對(duì)誤差分別為22%和25%。證明基于EMD 的SVR 方法能夠有效地對(duì)鐵路OD 日客流數(shù)據(jù)進(jìn)行預(yù)測(cè)，同時(shí)提高預(yù)測(cè)的準(zhǔn)確性。

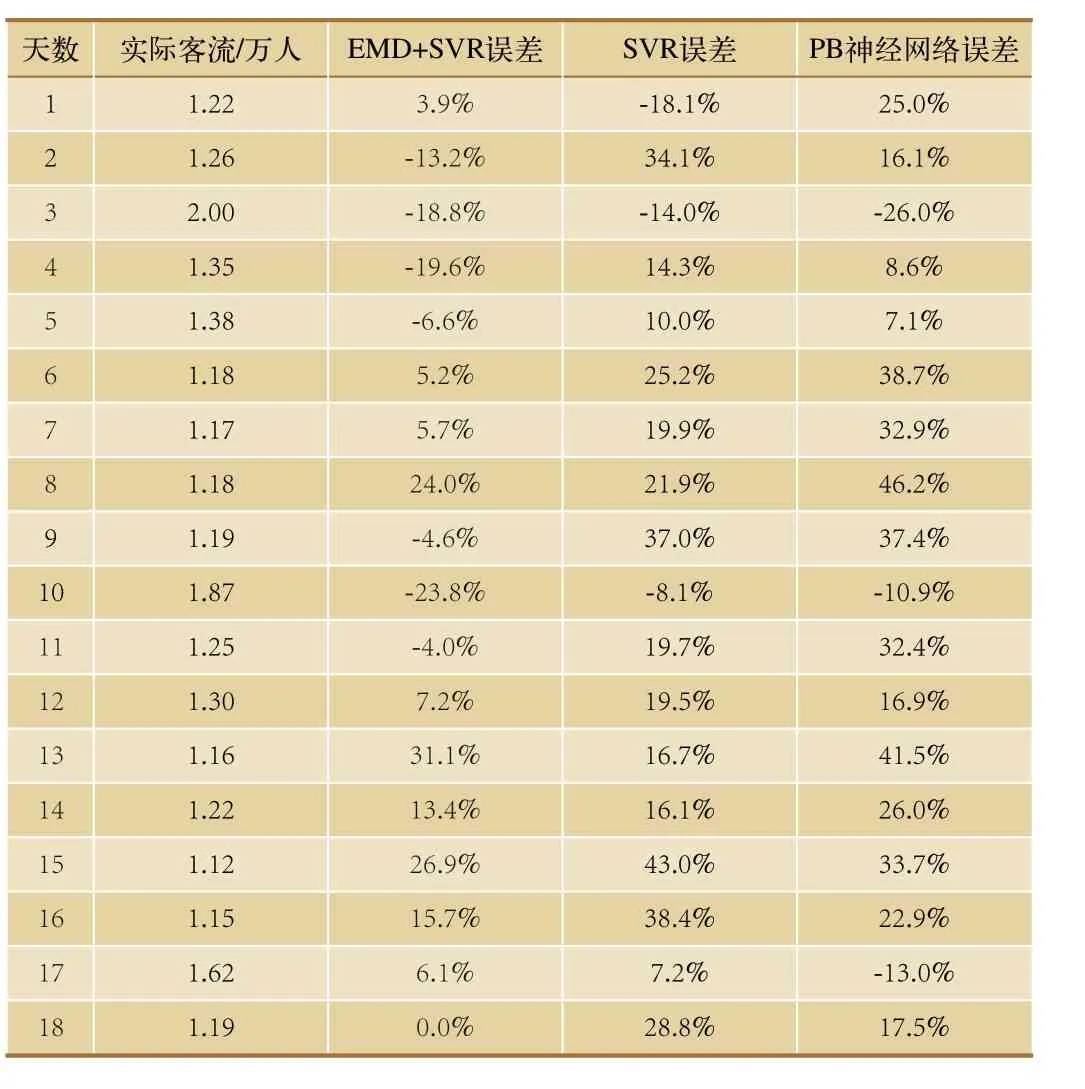
表3 各種預(yù)測(cè)方法相對(duì)誤差表

表4 各種預(yù)測(cè)方法絕對(duì)誤差表

3 結(jié)束語(yǔ)

數(shù)據(jù)實(shí)驗(yàn)結(jié)果表明，基于EMD 的SVR 方法能夠有效地對(duì)鐵路客流進(jìn)行預(yù)測(cè)，為實(shí)際應(yīng)用中的客流預(yù)測(cè)問(wèn)題提供了新的方法。本文對(duì)基于EMD 的SVR模型進(jìn)行構(gòu)建，并進(jìn)行學(xué)習(xí)和訓(xùn)練，利用OD 日客流對(duì)預(yù)測(cè)模型進(jìn)行檢驗(yàn)。通過(guò)對(duì)SVR、BP 以及基于EMD 的SVR 預(yù)測(cè)這3 種預(yù)測(cè)模型進(jìn)行仿真，結(jié)果表明，本文所建立基于EMD 的SVR 預(yù)測(cè)模型的預(yù)測(cè)誤差最小。因此，該預(yù)測(cè)模型可為鐵路客流的預(yù)測(cè)提供一定的實(shí)用價(jià)值。此外，為了更好的提高預(yù)測(cè)準(zhǔn)確性，需要對(duì)殘差進(jìn)行詳細(xì)分析，對(duì)于殘差的利用將是基于EMD 的SVR 方法下一步要研究的問(wèn)題。