剛性懸掛接觸網拉出值布置與受電弓磨耗分析

張權

（中鐵第一勘察設計院集團有限公司，陜西 西安710061）

我國新建城市軌道交通接觸網采用剛性懸掛方式以來，現場多次報道受電弓碳滑板磨耗不均勻問題，如廣州地鐵二號線受電弓在最大拉出值附近磨耗嚴重，形成較深凹槽。磨耗布局不合理，不僅會降低受電弓的使用壽命，還會造成接觸網拉弧、打火。研究表明，接觸網拉出值平面布置方式不合理是造成受電弓磨耗不均勻的主要原因[1]。因此，為保障電氣化鐵路的安全穩(wěn)定運行，需對剛性懸掛接觸網拉出值布置方式展開分析。

1 正弦波拉出值布置方式

圖1 為剛性懸掛接觸網拉出值按正弦波方式布置示意圖。圖中黑色點劃線為線路中心線，紅色實線由各個懸掛點拉出值擬合而成，其中A 為全線拉出值最大點，C、D 點為關節(jié)處懸掛點。由圖可知，拉出值采用正弦波方式布置時，線路兩側懸掛點個數幾乎相同，匯流排在線路兩側排布總長均等，理論上受電弓在線路上滑動時，碳滑板上兩半弓磨耗分布均勻。

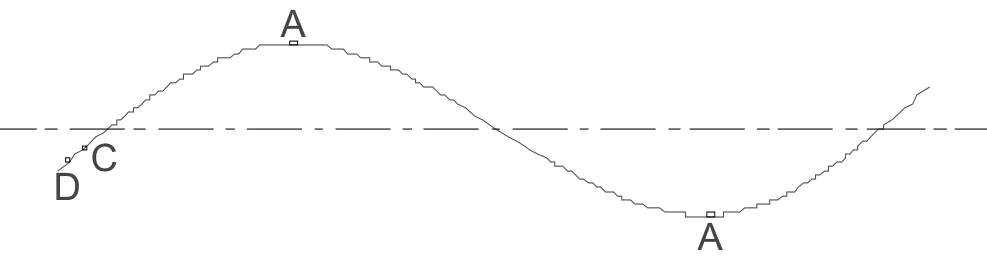
圖1 剛性懸掛正弦波拉出值布置示意圖

在正弦波布置方式下，拉出值計算：

式中，λ 為正弦波長度，在平面布置圖中等效為一個錨段長度；a 為最大拉出值，一般取值為250mm，x 為正弦波上任意一點與拉出值為0 的懸掛點之間的距離；y 為x 點處對應的拉出值。

2 類“之”字形拉出值布置方式

基于正弦波平面布置方式，本文通過進一步優(yōu)化，對接觸網拉出值采用類“之”字形布置，如下圖2 所示。圖中A 點為最大拉出值，一般取值為250mm；B 為次最大拉出值，通常條件下為230mm；C 點為錨段關節(jié)處懸掛點，距離錨段終端3.8m，拉出值為100mm（絕緣錨段關節(jié)為150mm）；D 點為錨段關節(jié)處懸掛點，距離C 點2m，拉出值取100mm（絕緣錨段關節(jié)為150mm）。

圖2 剛性懸掛類“之”字形布置示意圖

y1為任一懸掛點x 的拉出值，以非絕緣關節(jié)為例，AC 區(qū)段拉出值計算如下：

由于D、C 兩點拉出值相同，可認為受電弓在此時處于水平狀態(tài)，以C 點為原點建立坐標，則x 點處拉出值計算如上式（2）所示，式中xC為曲線上任意一點x 到C 點距離，LBC為B 點到C點距離，y1為x 點處拉出值。

同理，BB1 區(qū)段拉出值計算如式（3）所示：

式中，x0為BB1 區(qū)段上任意一點到拉出值為0 的點之間的距離，LBB1為BB1 之間距離，y2為x 點處拉出值。

3 兩種布置方式受電弓磨耗分析

標準匯流排長度為12m，為減少匯流排截斷浪費，錨段布置原則如下：5.95*2+12*n（標準匯流排長度12m，將其截斷為兩半，長度本應為6m，但考慮到施工過程中存在一定誤差，本文誤差考慮5mm，作為計算裕度）。匯流排長度不應超過250m，施工現場使用較多的主要是215.9、227.9、239.9。以215.9 標準錨段長度對接觸網平面布置展開分析討論。

3.1 正弦波布置方式磨耗分析

當一個錨段長度內只有一個正弦波時，不同拉出值位置處受電弓的磨耗距離如表1 所示。

表1 正弦波拉出值平面布置方式受電弓磨耗距離

由上表可見，在拉出值為200～250mm 范圍內，受電弓磨耗距離最大，其磨耗距離占正弦波百分比高達40%以上；其他拉出值變化范圍內，受電弓磨耗距離相差較小，磨耗距離與正弦波的百分比均在20%以下，且當懸掛點拉出值越接近0 時，相同拉出值變化范圍內受電弓磨耗距離占正弦波比例越小。

3.2 類“之”字形布置方式磨耗分析

下表為不同拉出值位置處受電弓的磨耗距離，假定某方向拉出值為正，則另一方向拉出值為負，將拉出值劃分為10 個區(qū)間。

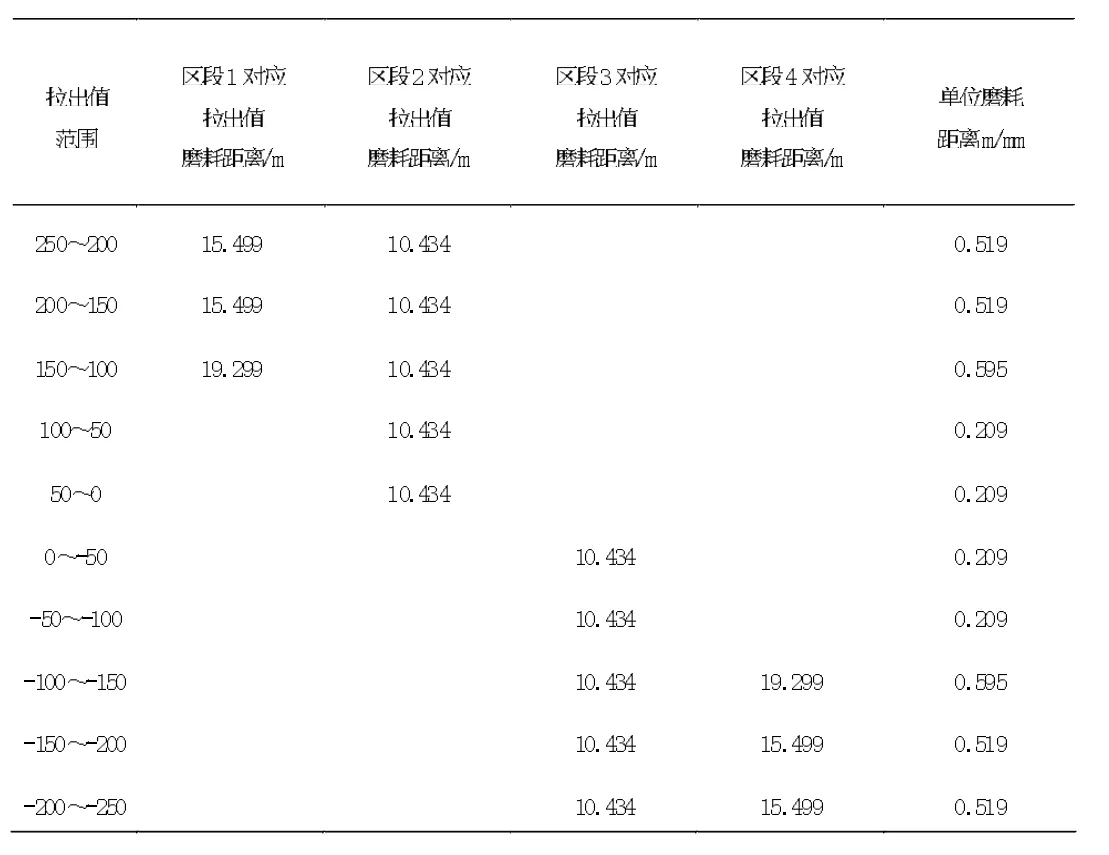
表2 一個正弦波范圍內受電弓磨耗距離

由表2 可知，在拉出值為0 附近受電弓磨耗距離較短，相應磨耗較輕，對其拉出值變化率進行計算發(fā)現，其變化率小，說明受電弓在拉出值為0 附近速度較快，并能實現平滑過渡；其他拉出值范圍內，磨耗距離幾乎相同，差距較小，說明受電弓在除拉出值為0 附近外，各個部位磨耗均勻。因此當接觸網拉出值采用此種類型平面布置方式時，受電弓不易損傷。

4 結論

基于傳統(tǒng)正弦波拉出值布置方式，剛性懸掛接觸網拉出值采用類“之”字形布置，懸掛點均勻分布在線路兩側，受電弓在一定區(qū)段相同移動距離情況下拉出值變化率一致，從而使受電弓磨耗均勻，在設計過程中具有一定的指導意義。