非牛頓流體在不規則管道中的流動特性研究＊

李亞飛，周懿，胡鉞，高政

非牛頓流體在不規則管道中的流動特性研究＊

李亞飛，周懿，胡鉞，高政

（船舶動力工程技術交通行業重點實驗室，湖北 武漢 430063；武漢理工大學 能源與動力工程學院，湖北 武漢 430063）

非牛頓流體被大量應用于工業生產中，如利用剪切稀化流體應用的醬類食品生產運輸、高分子聚合物在工業生產中的管道運輸及鉆井用洗井液完井液等。相比傳統的牛頓流體，關于非牛頓流體在管道內的流動的研究還有很大發展空間，因此對其機理的研究具有重要的現實意義。借助多物理場仿真軟件COMSOL Multiphysics，對非牛頓流體在不規則管道內的流動現象進行了數值模擬研究，分析了非牛頓流體在管道內的速度場分布、剪切應變速率分布以及黏度分布情況。結果表明，在同一不規則管道中，管內流動的非牛頓Carreau流體的剪切應變速率與黏度關系符合其本構方程特性，相比牛頓流體表現出了明顯較差的流動性，且速度場的分布一直保持一致；實驗組非牛頓流體的剪切應變速率量級比對照組牛頓流體小很多，解釋了兩種流體在速度場分布的差異性；驗證了Carreau流體構型中剪切應變速率與黏度的負相關關系。

非牛頓流體；管道；流動特性；冪律流體

非牛頓流體是剪切力與剪切應變率之間不是線性關系的流體。非牛頓流體的應用十分普遍，涉及采用剪切增稠液體的裝甲、食品工廠設計果醬類食品的運輸加工及高分子聚合物在化工生產中的運輸等諸多方面。這類非牛頓流體在工業生產方面的應用研究，直接影響工業生產效率及國家經濟，因此對非牛頓流體在管道中的流動機理具有較大的研究價值。

對非牛頓流體的研究方法包括實驗法、解析解法與數值解法。實驗法直接，但成本高且實驗普遍性不高。解析解法理論上為最理想的研究方法，通過建立合適的微分方程，使用純數學方法得出方程的精確解；但對于非牛頓流體復雜的流動情況來說，求解的難度過大。數值解法則是應用計算機將物理場離散化，之后將流體微分方程組轉化為代數方程并求出各個節點上的參數值，屬于一種近似解法。由于數值解法容易獲得且能保證足夠的求解精度，其已經成為研究非牛頓流體問題最為常用的方法。

本文選取一種注塑噴嘴模型作為研究對象，以COMSOL Multiphysics這一軟件作為計算平臺，采用有限元法對非牛頓流體流經不規則管道時表現出的流動特性進行數值模擬研究。在不規則腔體內，對照研究非牛頓Carreau流體與冪律牛頓流體的流動特性，討論非牛頓流體的剪切應變速率與黏度對于速度大小與速度場分布的影響。

1 管內流動數學模型

1.1 控制方程組

一切的流體流動過程，都以三個基本的物理學原理為基礎：質量守恒定律，牛頓第二定律與能量守恒定律。將這些物理學用于構建流動模型，將會導出一組方程，即連續性方程、動量方程與能量方程。這些方程是上述物理學原理的數學描述，本文不討論傳熱，因此不引入能量守恒方程：

質量守恒定律（連續性方程）：

式（1）表示瞬態三維可壓流體流動的連續性方程，本文所分析的流體流動處于穩態且不可壓縮，密度不會隨著時間的變化而改變，因此流體流動的數學描述為：

動量守恒方程：

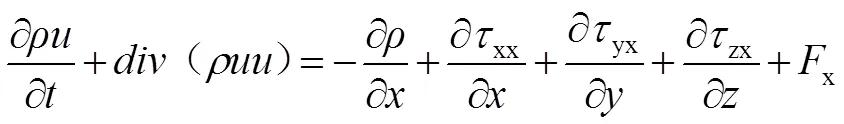
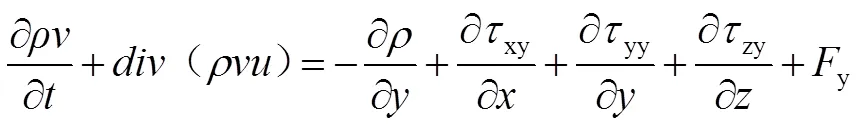
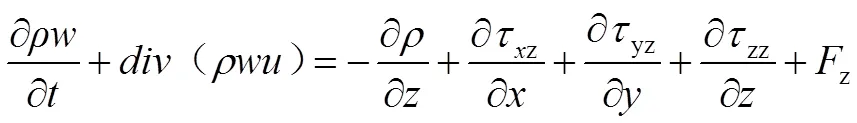
式（3）（4）（5）是對于任何流體都成立的動量守恒方程，是微元體內流體動量對于事件的變化率等于外界作用于該微元體上的各種力的和，簡稱動量方程，也稱納維斯托克斯（N-S）方程。

1.2 本構方程

本構方程是反映物料宏觀性質的數學模型，又被稱為流變狀態方程或是流變方程。在流變學中，本構方程是在某些假定條件下，對流體或彈性體的材料力學行為的數學描述，可用來區分流體類型。本構方程與連續性方程、運動方程一起構成封閉的方程組，用于求解流體的流動特性。

在本文仿真中使用的冪律流體的本構方程式如下：

式（6）中：為黏稠系數，表示物料的黏稠程度，Pa·sn；為冪律流變指數（簡稱冪律指數），為無量綱量，表示非牛頓流體的流動特性偏離牛頓流體的程度（=1時為牛頓 流體）。

1.3 非牛頓流體管道流動模型

剪切應變速率描述的是流體的剪切流動，定義為單位時間的剪切應變變化：

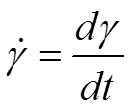
式（7）中：為剪切應變。

值得注意的是，剪切應變速率常與速度梯度混淆。實際上二者是不同的概念。速度梯度是流體的速度對空間坐標的導數，用/來表示。在數學上，二者的數值有時相等，這是因為一般速度梯度符合：

但二者的物理意義并不相同，且數值上有時并不相等（如流體在同軸圓筒之間的流動，此時有角速度的影響）。

2 物理模型及計算方法

在規則管道內，流體的速度場分布較為均勻，各流動特性參數的變化梯度較小。本文在這一部分選取一不規則管道腔體進行管道流動特性仿真，以更清楚地展示流體的流動特性。另選取適當的非牛頓流體與牛頓流體進行變量控制，構成實驗組與對照組。通過對比兩種流體的仿真結果，說明非牛頓流體不同于牛頓流體的流動特性。

2.1 物理模型

2.1.1 幾何模型

本組仿真的計算區域如圖1所示，為一個呈圓柱對稱的不規則彎曲管道腔體。流體由腔體的圓形入口處流入，中途流經一截面當量直徑較小的喉口，最后由腔體的環形出口處流出。腔體的總長度為42 mm，圓形入口直徑為18 mm，環形出口寬度為12 mm，其余具體幾何尺寸如圖2所示。A—B為管道進口段；F—G為管道出口段；B—C—D—E—F 與 G—H—I—J—A為管道壁面。使用此不規則腔體進行數值模擬的原因：在腔體喉口處由于其的截面當量直徑相對較小，流體經過時會出現較大的壓力梯度，進而顯著地影響速度、剪切率與動力黏度。所以在喉口當量直徑最窄處選取一個截面，計算分析兩種流體各項流動參數在這個截面上的分布，以更精確地說明流體的流動特性。截面具體位置如圖3所示。喉口處截面的位置與圖2中R12與R3圓心連線重合。

圖1 不規則管道腔體示意圖

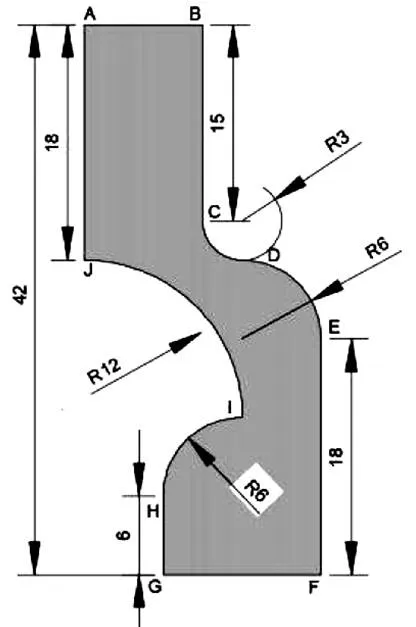
圖2 不規則管道腔體的具體尺寸（單位：mm）

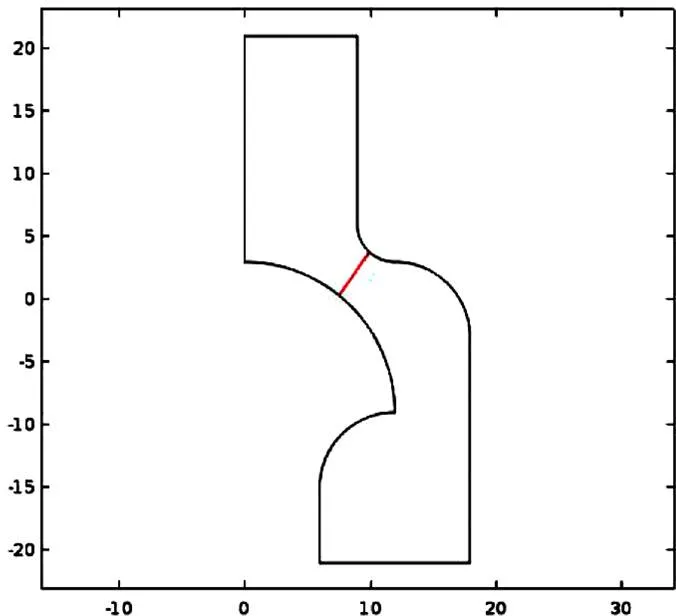
圖3 喉口處截面的位置（單位：mm）

2.1.2 流體性質

2.1.2.1 非牛頓流體性質（實驗組）

本組仿真計算所使用的非牛頓流體為線性聚苯乙烯在1-氯苯中的溶液（A solution of linear polystyrene in 1-chloronaphthalene），其被廣泛用于塑料制品制造中。該溶液在圖1中不規則腔體內的流動過程，可視為對塑料制品生產中注塑工序的溶液流經注塑噴嘴工段過程的模擬。該聚苯乙烯溶液屬于非牛頓Carreau流體，其黏度eff與流體剪切應變速率相關，具體關系式如下：

式（9）中：0為零剪切應變速率時的黏度；inf為無限大剪切應變速率時的黏度；為松弛時間，s；為模型指數。

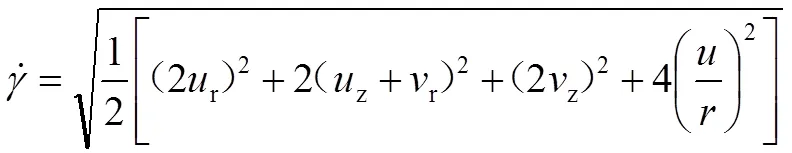
本溶液的相關非牛頓Carreau流體模型參數值與仿真需要的其他物性如表1所示。對照組牛頓流體的物性參數值如表2所示。

2.1.2.2 牛頓流體性質（對照組）

根據控制單一變量的原則，本組仿真所使用的對照組牛頓流體只進行黏度相關系數的調整，其他物性參數與實驗組非牛頓流體保持一致。對照組牛頓流體使用冪律流體模型，冪律指數=1。當冪律指數=1時，流體的黏度eff實際上固定為1 Pa·s。

表1 線性聚苯乙烯在1-氯苯中的溶液的物性參數值

參數名參數值 零剪切應變速率時黏度μ00 無限大剪切應變速率時黏度μinf /（Pa·s）166 松弛時間λ/s1.73×10-2 Carreau模型指數n 0.583 密度ρ/（kg/m3）450

表2 對照組牛頓流體的物性參數值

參數名參數值 稠度指數m1 冪律指數n1 最低剪切應變速率/s-10.01 密度ρ/（kg/m3）450

2.2 邊界條件

進口邊界條件：進口為圖2中A—B段。設定進口壓力in，取值從10 kPa開始，以40 kPa的梯度遞增至210 kPa，模擬不同進口壓力下實驗組與對照組流體的流動特性。

出口邊界條件：出口為圖2中F—G段，設定出口壓力為0。

壁面邊界條件：壁面為圖2中B—C—D—E—F與G—H—I—J—A段。設定無滑移邊界條件，即壁面處的流體速度為0。

無黏性應力條件：·[（▽+（▽）T）]。

其他：流體不可壓縮；所有管道區域內實驗組非牛頓流體處于層流狀態，進口壓力較大時，對照組牛頓流體會出現湍流。

2.3 求解器介紹

本次模擬使用的COMSOL Multiphysics是一款功能強大的多物理場仿真軟件，可以對多個領域的物理過程進行模擬計算。

本文研究的是非牛頓流體在管道內的流動特性，因此選用的是COMSOLMultiphysics中的Laminar flow求解器模塊。這個模塊內置了許多流動的基本物理參數，可以在這些參數的基礎上結合前文所述的數學模型定義更多仿真所需要的變量。

2.4 數值計算方法

本文涉及的數值計算使用的是有限元分析法（Finite element method，FEM）。它的基本思路為：一個物體或系統被分解為由多個相互聯結、簡單、獨立的點組成的幾何模型。在這種方法中這些獨立的點的數量是有限的，因此被稱為有限元。由實際的物理模型中推導出來的平衡方程式被使用到每個點上，由此產生了一個方程組，這個方程組可以用線性代數的方法來求解。

3 仿真結果分析

3.1 兩種流體的速度場對比

當進口壓力分別為10 kPa、90 kPa、170 kPa時，從實驗數據分析可知，隨著進口壓力的增大，牛頓流體的速度場分布情況發生了較為明顯的變化。進口壓力為10 kPa時，流體速度在腔體入口段達到最大值，喉口處的中心速度也達到了局部峰值，喉口段之后的流體速度漸緩。進口壓力增大時，腔體入口段的速度場分布情況差異不大，但喉口處的局部速度峰值與入口段的速度最大值之間的梯度差異會逐漸減小，最終在喉口處達到全局速度最大值。在進口壓力為90 kPa時，速度入口段的速度最大值約為 57.669 m/s，喉口處速度峰值則在52.111 m/s附近；進口壓力為170 kPa時，速度入口段的速度最大值約為82.369 m/s，喉口處速度峰值則已經達到85.698 m/s。此外，喉口后部的擴散段速度場分布也隨著進口壓力增大而出現較為明顯的差異。當進口壓力為90 kPa時，喉口處的速度峰值區域已經開始變得狹長，峰值點更接近下方壁面。峰值區域狹長化和峰值點向下方壁面移動的程度隨著進口壓力進一步上升而強化，這一特點從進口壓力達到170 kPa之后就非常明顯。另一方面，流場內流體速度的絕對值也隨著入口壓力的增加出現明顯的上升。速度峰值由10 kPa入口壓力時的2.746 m/s上升至90 kPa入口壓力時的57.669 m/s，在170 kPa時則是82.369 m/s。

不同進口壓力下非牛頓流體的速度場分布如圖4所示。從圖4可以看出，在進口壓力為10 kPa時，非牛頓流體的速度場分布與牛頓流體的分布情況相似；但隨著進口壓力的增加，非牛頓流體的速度場分布并不會出現明顯變化，這與牛頓流體不同。此外，非牛頓流體的速度絕對值也遠小于牛頓流體，進口壓力為10 kPa時速度峰值約為0.015 m/s，進口壓力為90 kPa時速度峰值約為0.157 m/s，進口壓力為 170 kPa時速度峰值約為0.346 m/s。很明顯，實驗組的非牛頓流體流動性相比對照組的牛頓流體要差得多。

造成這種流動性差異的原因可以通過比較兩種流體的剪切應變速率和黏性來得出。非牛頓流體剪切應變速率的分布情況如圖5所示。

從實驗數據中可得牛頓流體的剪切應變速率值遠大于非牛頓流體的（3個數量級的差異），說明單位時間內牛頓流體的剪切應變變化量更多，表現為較高的流速；非牛頓流體則相反。

另外，如前文所述，對照組牛頓流體由于冪律指數=1，所以流體的黏度大小固定為1 Pa·s；而實驗組非牛頓流體的黏度由Carreau模型決定，為一個與剪切應變速率呈負相關的變量，其具體大小與分布如圖6所示。可以清楚地得出，實驗組非牛頓流體的黏度遠遠大于對照組牛頓流體的黏度，大部分區域黏度值達140 Pa·s以上，這也可以解釋非牛頓流體的流動性為何遠不如牛頓流體。

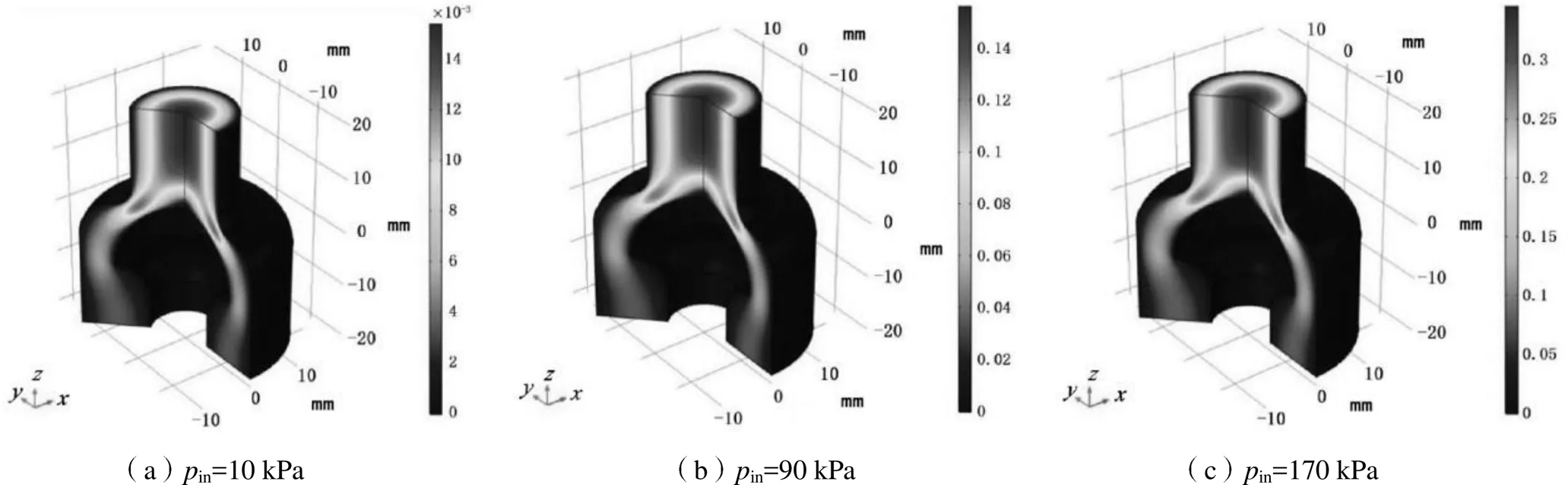
圖4 不同進口壓力下非牛頓流體的速度場分布

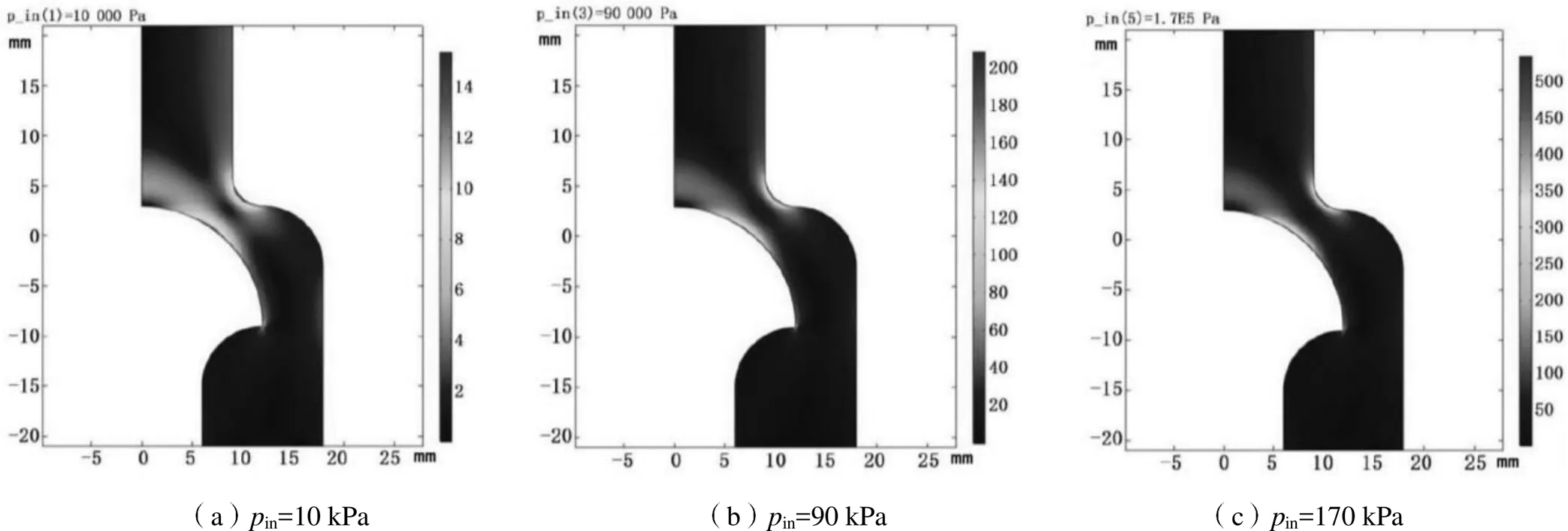
圖 5 不同進口壓力下非牛頓流體的剪切應變速率分布

圖6 不同進口壓力下非牛頓流體的黏度分布

3.2 喉口截面處的流動特性對比分析

從之前對兩種流體速度場的分析可以得知，速度、黏度等變量在流動區域的喉口處均會出現比較明顯的梯度變化。利用流動腔體圓柱對稱的特性，通過二維函數圖像即可確定各項流動參數在喉口處截面上的分布。

兩種流體流速沿喉口截面徑向的分布曲線如圖7和圖8所示。

圖7與圖8所反映的速度大小變化情況，與前文圖5反映的喉口處速度場分布相符。隨著進口壓力的增大，喉口處的流體流速也相應增加。圖7中各條速度線的峰值，對應的是實驗中牛頓流體的喉口處局部速度峰值；峰值位置的橫坐標隨進口壓力增大而向左橫移，對應的是實驗時牛頓流體局部速度峰值點區域隨進口壓力增大的下移。圖8中各速度線峰值橫坐標則幾乎沒有出現橫移的現象，也符合圖4中非牛頓流體不同進口壓力下速度場分布大致相同的情況。

從式（9）與式（10）可以看出，實驗組非牛頓流體的速度分布與剪切應變速率分布呈正相關，剪切應變速率的分布又與黏度分布呈負相關。為了驗證這兩組關系，繪制實驗組流體的剪切應變速率與黏度沿截面徑向的分布曲線，如圖9、圖10所示。

從圖9、圖10可以看出，隨著進口壓力增大，實驗組非牛頓流體在截面上的剪切應變速率曲線逐漸上凹，黏度曲線逐漸下凸。速度曲線與剪切應變速率曲線的變化方向相同，剪切應變速率曲線又與黏度曲線變化的趨勢相反，這就驗證了由式（9）與表1數據所表示的剪切應變速率與黏度之間的負相關關系。

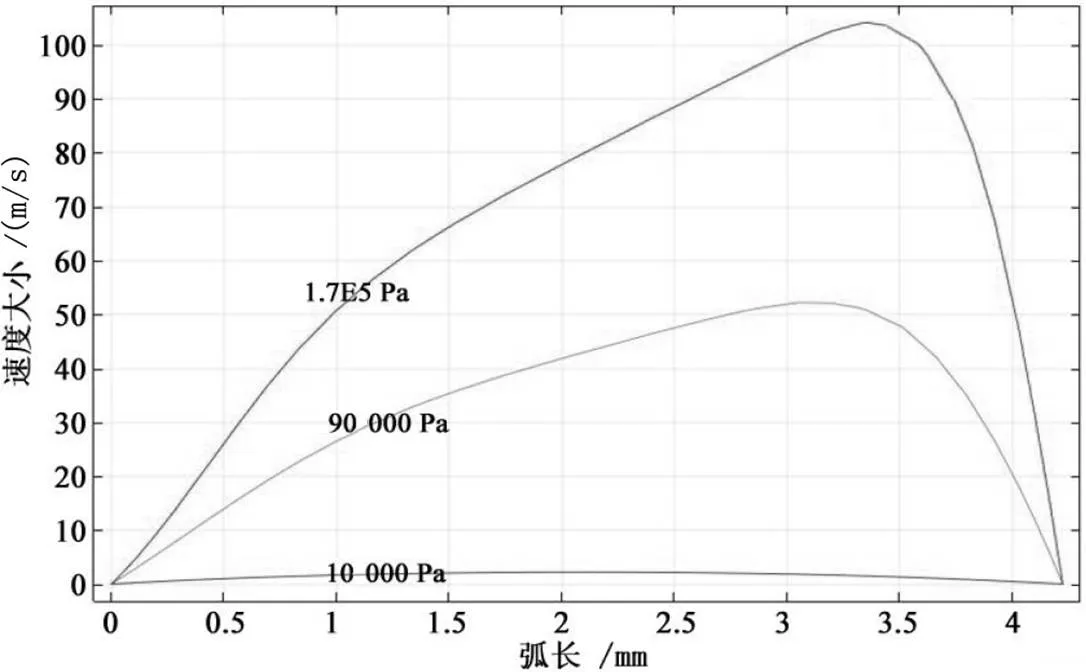
圖7 牛頓流體在截面上的速度分布

圖8 非牛頓流體在截面上的速度分布

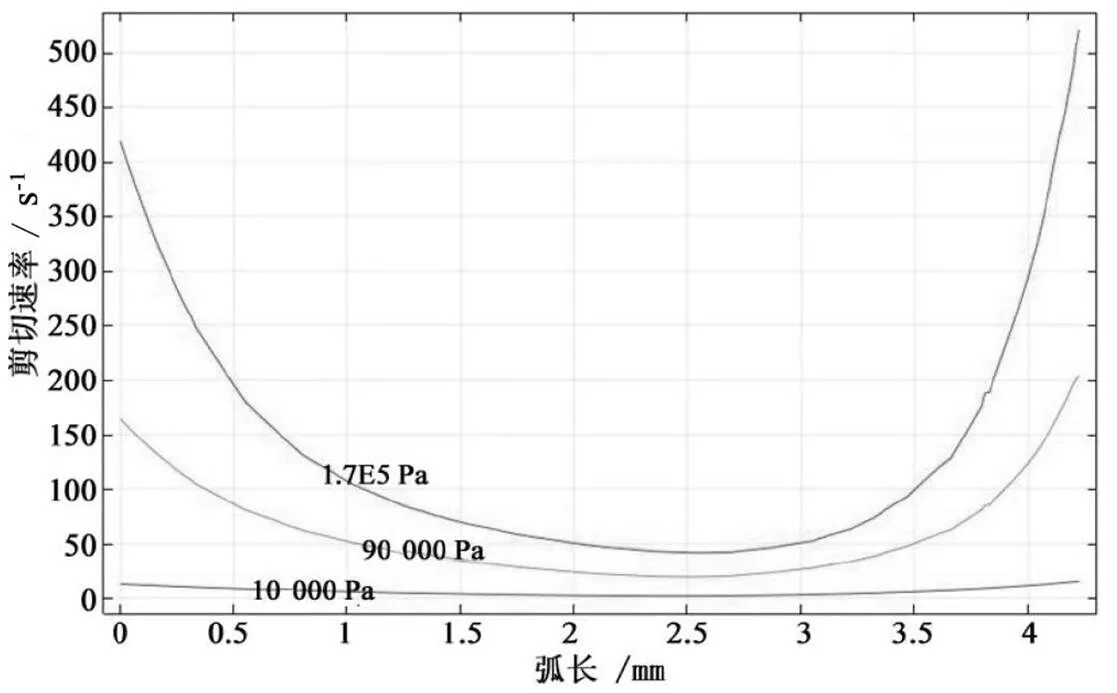
圖9 非牛頓流體在截面上的剪切應變速率分布

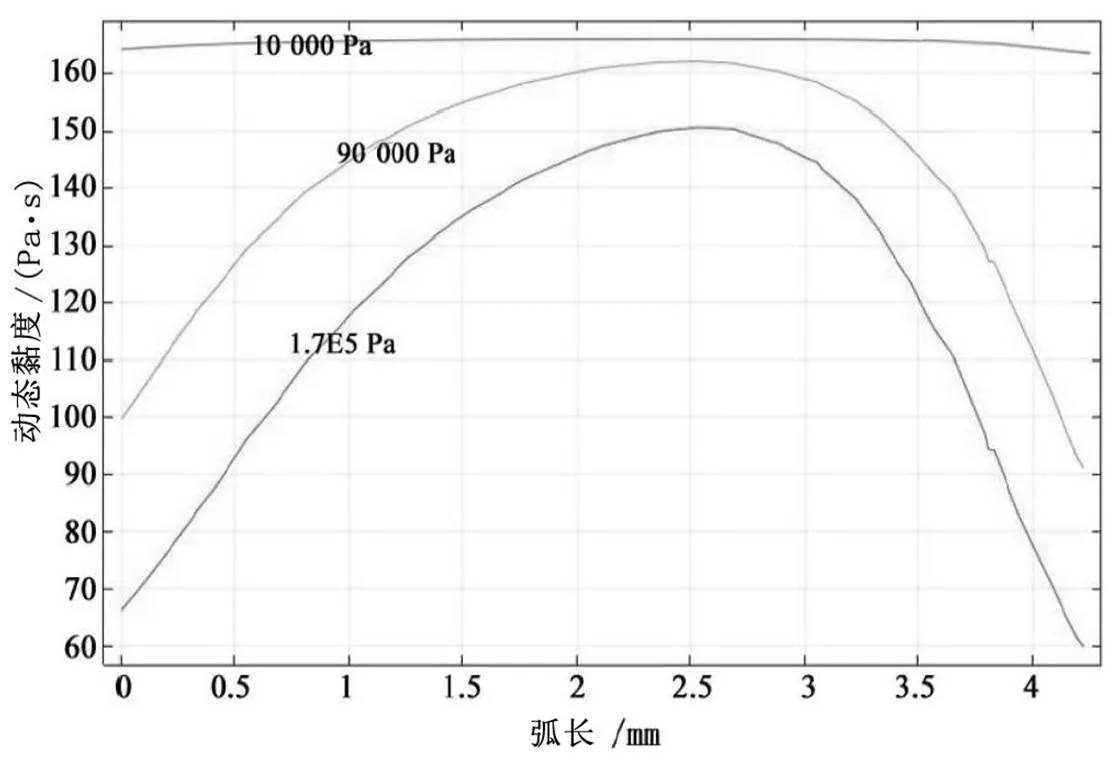
圖10 非牛頓流體在截面上的黏度分布

4 結論

本文通過 COMSOL Multiphysics平臺，使用有限元法與局部優化網格技術，建立了非牛頓流體在不規則管道腔體內的流動模型。通過以上數值模型，分析了非牛頓流體在管道內的速度分布、剪切應變速率分布及黏度分布，并討論了流體流動特性參數之間的關系。

具體總結如下：①隨著進口壓力的增大，對照組牛頓流體的流速不斷提高，速度場的分布中出現狹長狀局部峰值區域；實驗組非牛頓流體流速一直非常小，表現出很差的流動性，且速度場的分布情況一直保持一致。②在高速管道流動中，非牛頓Carreau流體的剪切應變速率遠小于牛頓流體，進而導致其黏度比牛頓流體的黏度大得多，表現為管道內極差的流動性與不隨進口壓力變化而改變的速度場分布。③通過對喉口處非牛頓流體的剪切應變速率與黏度分布曲線的分析，驗證了Carreau流體構型中剪切應變速率與黏度的負相關關系。

O373

A

10.15913/j.cnki.kjycx.2020.08.009

2095－6835（2020）08－0024－05

國家自然科學基金青年科學基金項目（編號：51806157）

李亞飛（1998—），男，湖北武漢人，本科在讀。

〔編輯：嚴麗琴〕