滲透函數(shù)思想 探究導(dǎo)數(shù)雙零點問題*
高 軍
(廣東省深圳市高級中學(xué) 518040)
函數(shù)思想是中學(xué)數(shù)學(xué)的基本思想之一,是用運動和變化的觀點分析和研究數(shù)學(xué)中的數(shù)量關(guān)系,建立函數(shù)關(guān)系或構(gòu)造函數(shù),運用函數(shù)的圖象和性質(zhì)去分析問題轉(zhuǎn)化問題,從而使問題獲得解決的一種重要數(shù)學(xué)思想,它貫穿于整個中學(xué)數(shù)學(xué)的教學(xué)與研究中. 導(dǎo)數(shù)中的雙零點問題是各類型考試中的熱點題型,尤其是這樣一類問題:已知含有ex或lnx的函數(shù)f(x),且存在x1,x2,x1≠x2,滿足f(x1)=f(x2),證明有關(guān)x1與x2的不等式或求某個參數(shù)的取值范圍,這類問題倍受命題人的青睞. 本文以一道雙零點導(dǎo)數(shù)問題為例,滲透函數(shù)思想,探究此類問題的解題方法與策略,與讀者交流.
1 問題呈現(xiàn),解法探究
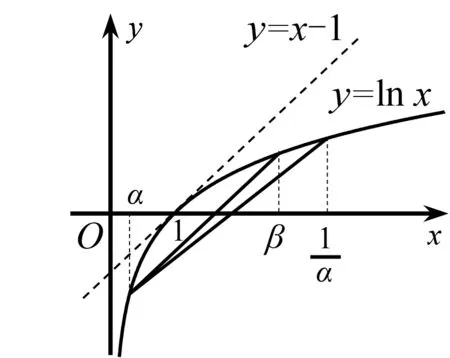
問題呈現(xiàn) 已知f(x)=ex-ax+a,若f(x)的圖象與x軸交于兩點(x1,0),(x2,0) (x1 (1)求實數(shù)a的取值范圍; (2)求證:x1x2 解法探究 (1)實數(shù)a的取值范圍為(e2,+∞)(過程略). (2)先證明不等式x1x2 思路1 重組設(shè)元,整體構(gòu)造,滲透函數(shù)思想 解由題意,ex1=ax1-a①,ex2=ax2-a②. ①×②,得ex1+x2=a2(x1-1)(x2-1)=a2(x1x2-x1-x2+1). ①-②,得ex1-ex2=a(x1-x2). 構(gòu)造函數(shù)h(t)=et-e-t-2t.h′(t)=et+e-t- 2≥0,所以h(t)在(-∞,0)上單調(diào)遞增,所以h(t) 思路2 根據(jù)形式,類比構(gòu)造,滲透函數(shù)思想 解由題意,得ex1=ax1-a,ex2=ax2-a,兩式兩邊取對數(shù),得x1=ln(x1-1)+lna①,x2=ln(x2-1)+lna②. 思路3 結(jié)合圖形,巧妙構(gòu)造,滲透函數(shù)思想 由于x1x2 圖1 思路4 消參換元,主元構(gòu)造,滲透函數(shù)思想 故m′(t)在(0,1)上單調(diào)遞增,從而m′(t) 從而m(t)>m(1)=0,因而g′(t)<0,g(t)在(0,1)上單調(diào)遞減. 評注消去參數(shù)a,引入中間變量t,用變量t表示x1,x2,結(jié)論中的二元不等式變?yōu)橐詔為主元的一元不等式,構(gòu)造相應(yīng)函數(shù),研究函數(shù)單調(diào)性,用洛必達法則讓問題得到解決. 下面證明:x1+x2<2lna. 分析 由題意,得ex1=ax1-a,ex2=ax2-a,兩式兩邊取對數(shù)得,x1=ln(x1-1)+lna①,x2=ln(x2-1)+lna②.由①+②得x1+x2=ln(x1-1)(x2-1)+2lna. 要證x1+x2<2lna,只需證ln(x1-1)(x2- 1)<0,即證x1x2 思路5 極值偏移,對稱構(gòu)造,滲透函數(shù)思想 解f′(x)=ex-a,若a≤0,則f′(x)>0,故f(x)在R上單調(diào)遞增,不合題意. 若a>0,由f′(x)>0得x>lna,由f′(x)<0得x 若f(x)有兩個零點,則f(lna)=eln a-alna+a<0,故a>e2且x1 (1)含有雙變量且有參數(shù)的雙零點問題,綜合性強、難度大,問題的切入角度廣泛,學(xué)生較難掌握.解決該類問題的主要思路是將條件和結(jié)論進行適當變形與轉(zhuǎn)化,結(jié)合具體的結(jié)構(gòu)形式與特點構(gòu)造新函數(shù),將雙變量問題轉(zhuǎn)化為單變量的函數(shù)問題來解決. (2)數(shù)學(xué)思想是數(shù)學(xué)的靈魂與精髓,是知識轉(zhuǎn)化為能力的橋梁和紐帶.在解決導(dǎo)數(shù)的雙零點問題中,每種思路方法都滲透著函數(shù)思想,體現(xiàn)了函數(shù)思想在解題中的重要作用.在平時教學(xué)過程中,教師要有意識、有目的地在教學(xué)中滲透數(shù)學(xué)思想,這有利于提高學(xué)生分析問題解決問題的能力,有利于提升學(xué)生的數(shù)學(xué)學(xué)科核心素養(yǎng). (3)素養(yǎng)導(dǎo)向的高考命題注重科學(xué)探究能力的考查,有必要研究開發(fā)探究型、開放型試題,發(fā)揮各種題型的組合功能,拓展學(xué)生思維空間.注重一題多解、一題多法,拓寬學(xué)生的解題思路,引領(lǐng)學(xué)生多角度自主探究,促使學(xué)生熟練掌握多種數(shù)學(xué)方法,提升數(shù)學(xué)解題技能與課堂效益,激發(fā)學(xué)生學(xué)習(xí)潛力. 下面是問題的變式題,讀者不妨借用上述不同的解決問題思路試一試. 變式1 已知f(x)=ex-ax,若f(x)的圖象與x軸交于兩點(x1,0),(x2,0),(x1 變式2 已知函數(shù)f(x)=lnx-ax有兩個不同零點x1,x2,求證:x1x2>e2. 變式3 已知函數(shù)f(x)=(lnx-k-1)x,若x1 變式4 (2016年新課標Ⅰ卷理21題改編)已知函數(shù)f(x)=(x-2)ex+a(x-1)2有兩個不同零點x1,x2,求證:x1+x2<2.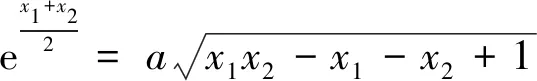
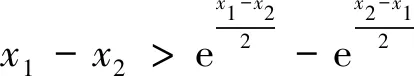
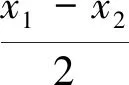
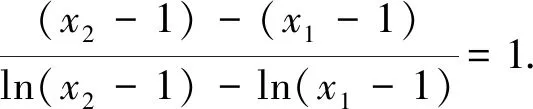
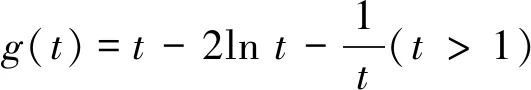
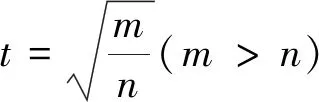
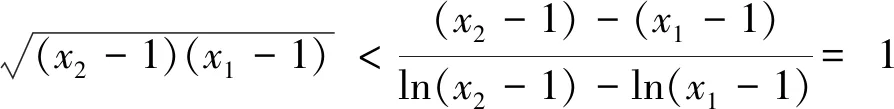
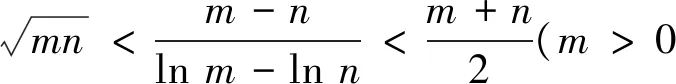
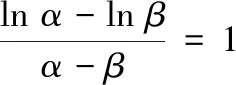
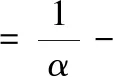
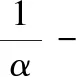
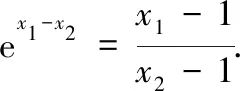
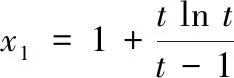

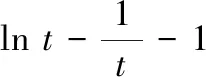
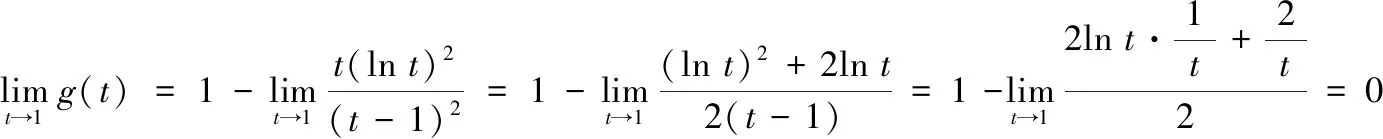
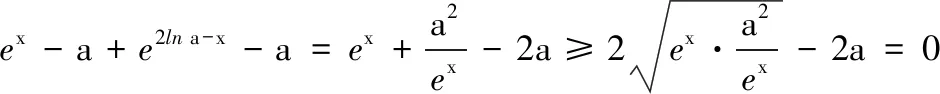
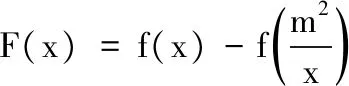
2 歸納總結(jié),反思感悟
3 借石攻玉,變式探究