水利工程施工成本動態控制方法研究

王 健

(朝陽縣水利勘測設計隊，遼寧 朝陽 122000)

0 引 言

水利工程項目管理中施工成本控制發揮著重要作用，施工企業的生存發展和建設項目的成敗直接與成本控制效果相關[1]。然而，項目施工過程中往往存在許多不確定性、復雜多變的影響因素，在施工前揭示各成本因素與總成本之間的關聯關系、預判其影響程度及制定成本控制策略等存在較大的難度[2-5]。目前，關于成本控制的相關研究主要體現在如下方面：①將施工成本影響因子采用決策樹、熵權、相關系數和相對重要性指數等方法判斷其重要程度，這些方法均是依靠專家的專業素養和知識經驗定性評價各風險因子，對各因素的量化評價存在較大的難度；②將項目成本控制因素從費用組成的角度分析，這種分析方法具有較強客觀性，但對大量的成本數據很難通過簡單的統計核算得到充分的利用。因此，為揭示各成本要素之間的關聯特性及其重要程度，實現項目成本的科學控制，必須對成本主要影響因素依據盡可能多的成本數據做出客觀地判斷，通過實施主動控制從根本上解決問題。鑒于此，文章利用在數據處理方面具有明顯優勢的粗糙集理論，揭示施工成本各要素之間的依賴關系，將成本指標的屬性重要度基于可辨識矩陣進行計算，然后通過屬性約簡獲取總成本與各成本要素間的關聯規則，可為水利工程施工單位的成本控制和方案優選提供科學指導[6]。

1 施工成本動態控制問題分析

1.1 施工成本控制指標體系

各項施工活動產生的費用即為工程成本，為減少不利的成本偏差有必要合理控制成本活動，該過程即為成本控制。通過對施工企業的實地考察及其主要管理部門的分析，從施工企業組織結構的角度建立基于活動的成本控制指標體系，見表1所示。

1.2 基于粗糙集的控制模型

在分類功能保持不變的條件下，粗糙集理論的主要思想為通過知識約簡獲取問題的決策規則與分類，由此得到有用的知識，基于粗糙集理論的成本動態控制模型見圖1所示。根據各指標屬性將其分為非數值型和數值型兩類，因此需要離散化處理各成本指標在歷史各期的標準值與實際值。決策信息系統的條件屬性為離散化處理后的成本偏差指標，相應的決策屬性為總成本控制效果，由此建立水利工程成本決策系統。成本信息中隱藏的規律性知識利用簡約、規則獲取算法和粗糙集的可辨識矩陣挖掘，根據成本變動情況制定有效的控制措施，通過對成本標準值的調整結束當前控制期。將本期統計的成本信息作為下個控制期間開始時的增加對象，在企業成本管理預測水平下補充進成本決策信息系統，按照該流程反復循環，及時補充、更新信息。參與系統分析的對象隨著工程進度的推進不斷增大，能夠獲取的有關信息也越來越多，從而反映工程成本管理水平。

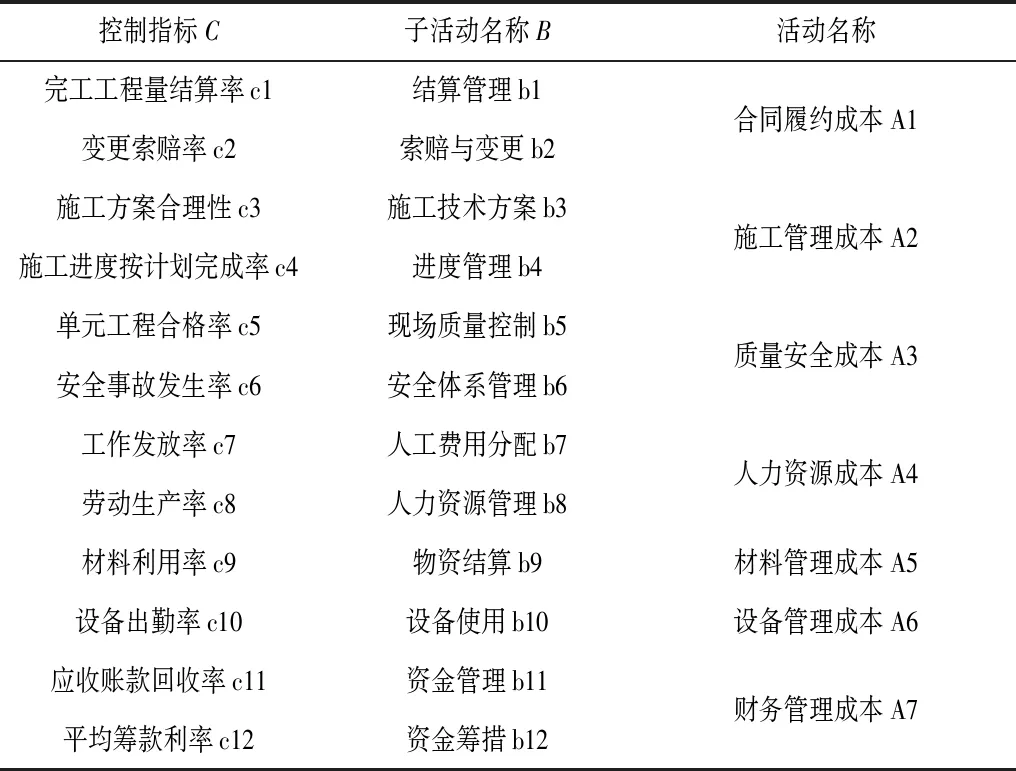
表1 成本控制指標體系

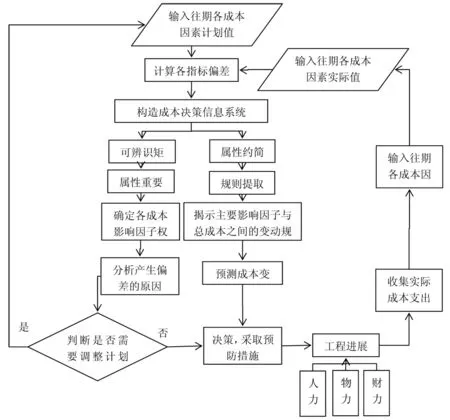
圖1 施工成本動態控制流程

2 基于粗糙集的施工成本控制方法

2.1 成本決策信息系統

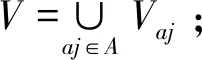
2.2 可識別矩陣

針對決策屬性值在信息系統S=(U,C∪D,V,f)中的不同對象，所有條件屬性在對象xi與xj之間的區別集表示為c(xi，xj)。定義n×n階可辨識矩陣為M，利用下式求解矩陣中的各值，即：

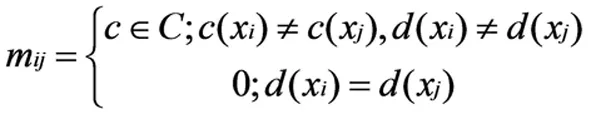
(1)

式中：d(xi)、c(xi)分別為紀錄在D上的值和屬性c上對象xi的值。

考慮到為對稱可辨識矩陣的特性，因此只需對下或上三角部分計算。一方面，可辨識矩陣的區分能力隨著出現屬性次數的增多而增強，相應的重要性越高；反之，則對決策信息系統的重要性越弱。另一方面，每個mij中包含的屬性在可辨識矩陣中越少，則屬性重要性越強；反之，則對決策信息系統的重要性越弱。所以，為求解各屬性的重要度可依據各成本屬性在可辨識矩陣中的出現次數判別。

2.3 成本控制策略分析

1)成本因素重要度。屬性關于知識表述的重要可利用屬性重要度來描述，即反映在整個系統中的重要地位。定義下述計算公式反映屬性重要度，即：

(2)

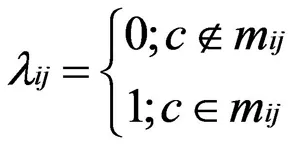
式中：|mij|為屬性個數。

根據歸一化處理公式和各成本屬性的重要度sig(c)，可確定水利工程施工成本各要素的權重，即W=(w1,w2,…,wn)。

2)成本屬性約簡。屬性約簡就是在所有屬性組成的集合中去除知識表達系統中冗余的信息，在不改變系統特性的條件下通過簡化分類器找出一個能夠最大限度的包含屬性全集分類信息的屬性子集，從而提高分類器的泛化性能和噪聲數據對分類知識發現的影響，為工程決策規則提供數據依據。采用布爾運算和邏輯運算的約簡算法，找到可辨識矩陣的核與約簡，其中約簡的交際即為核。然而，該方法在對象和屬性較多的決策信息系統中，其計算過程較為復雜。

粗糙集存在上、下兩個近似集，其中上近似、下近似分別為與X的交為非空初等集合的并和所有包含于X的初等集合的并，即上近似的元素可能屬于或不屬于X，而下近似的所有元素均屬于X。邊界域即為上、下近似的差，邊界域為空時X為精確集。

設存在非空有限集為U，U中的等價關系表示為R，其中X∈U。引入近似空間為K={U,R}，X的R上、R下近似集分別表示為R-(X)={X∈U∶[X]R?X}、R-(X)=(X)={X∈U∶[X]R∩X≠φ}，其中元素在等價關系R下構成的集合為[X]R，X的邊界域表示為BnR(X)=R-(X)-R-(X)，X的R正域、負域分別為PPOSR(X)=R-(X)、NNegr(X)=U-R-(X)。

滿足條件獨立性為一個屬性約簡的基本要求，即一個決策系統與一個非空約簡R∈C相對應，R獨立的判別條件為?c∈R，PPOSR-c=PPOSR(D)，其中D的R正域表示為PPOSR(D)。對此有學者給出了約簡定義，即：對于給定的S=(U,C∪D,V,f)，對?R∈C，判定R是一個Pawlak簡約時應滿足如下兩個條件，PPOSC(D)=PPOSR(D)和?c∈R，PPOSR-c(D)=PPOSR(D)。

2.4 決策規則的提取

從數據庫中挖掘有價值的、潛在的規律即為規則獲取，規則可作為屬性值之間的關系在知識表達系統中的數據模式，在粗糙集理論中數據的規則或模式主要是依據無法分辨關系隱含的數據粒度結構來發掘，由此獲取不確定及確定的決策規則。將決策規則按照屬性簡化表可表示為IF…，THEN…的形式，即在滿足一定的條件下確定相應的決策規則。

3 實例應用

某大型水利工程由施工企業承包，該企業下屬一個機械隊、一個鉆隊、兩個運輸車隊以及財務、設備、材料、人力資源、質量安全、工程技術、合同7個管理部門。施工內容主要有上壩料的碾壓、推平、裝運及挖掘。選擇該施工項目2015年2-9月成本數據為基礎，對其成本控制情況采用基于粗糙集理論的控制模型進行決策推理和評價分析。

1)數據預處理。根據施工企業的資質、信譽及歷史資料，按照成本控制指標體系提取企業各參數目標值，如表2所示。預處理各成本因素的實際值與計劃值之間的偏差，偏差為正、負時賦值分別為1、0，分別代表節約和超支；關于決策屬性，若總成本實際值大于或小于計劃值，則代表超支或節約。成本決策信息系統經預處理后的結果見表2。

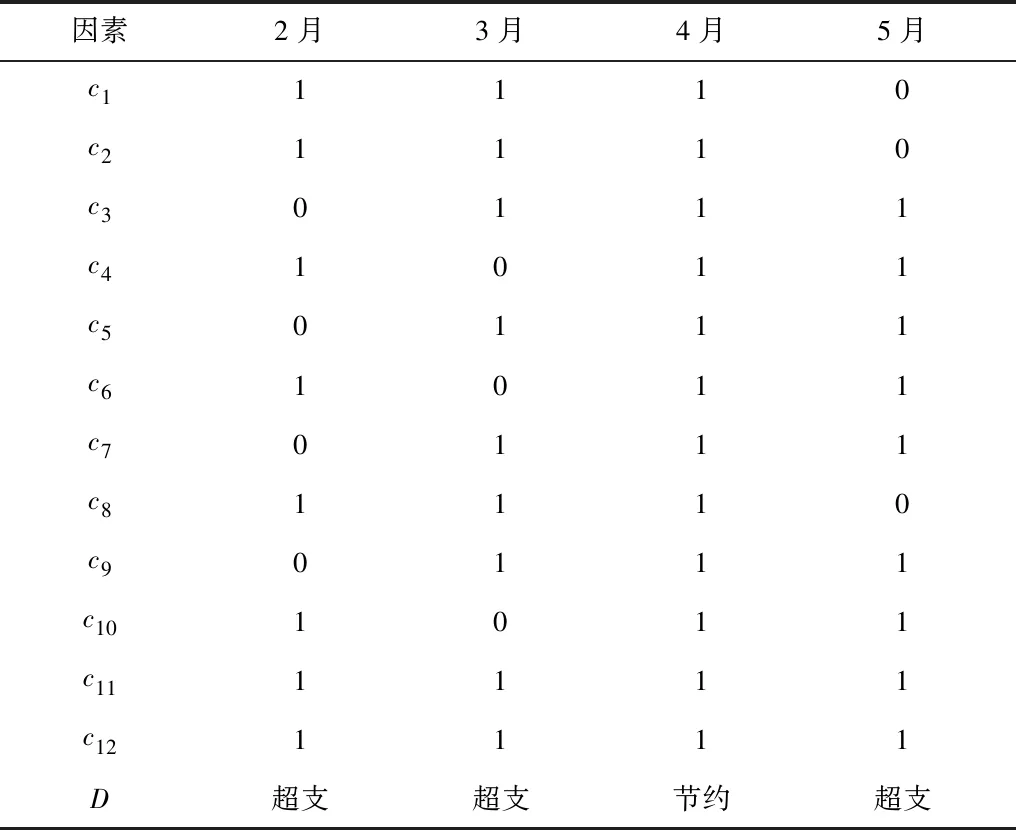
表2 成本決策信息系統及各因素計劃值

2)各指標權重計算。對可辨識矩陣利用文中所述公式(1)計算確定，即：

采用計算公式(2)求解上述矩陣，經標準化處理得到各參數權重，結果如表4。從表4可以看出，該水利工程的總成本受進度是否按計劃完成的影響最為顯著，貢獻率占12.8%；變更索賠率、完工工程量結算率、勞動生產率以及應收賬款回款率占比分別為9.6%、9.6%、7.9%、12.0%；材料利用率平均和施工方案是否合理占比7.8%、工資發放率和單元工程合格率占7.7%；平均籌款率對企業總成本貢獻率為7.1%，而企業總成本受設備出勤率和安全事故發生率的影響最小，占比分別為5.0%。

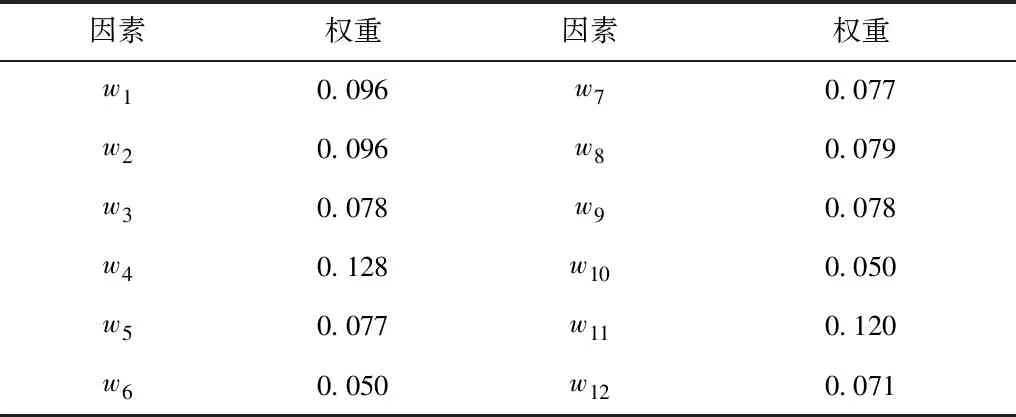
表4 水利工程施工總成本各因素權重

3)獲取成本決策規則和成本屬性約簡。對成本決策系統利用Rosetta軟件進行屬性簡約，結果為{c1，c3，c4}，由此可見為冗余屬性主要有c12、c11、c10、c9、c8、c7、c6、c5、c2。通過指標簡化設置規則可信度>0.75，覆蓋度>0.05，從而獲取6條決策規則：①AND施工進度是否按計劃完成c4(1)AND施工技術是否先進c3(0)，IF完工工程量結算率c1(1)THENd(總成本超支)；②AND施工進度是否按計劃完成c4(0)AND施工技術是否先進c3(1)，IF完工工程量結算率c1(1) THENd(總成本超支)；③AND施工進度是否按計劃完成c4(1)AND施工技術是否先進c3(1)，IF完工工程量結算率c1(1)THENd(總成本節約)；④AND施工進度是否按計劃完成c4(1)AND施工技術是否先進c3(1)，IF完工工程量結算率c1(0) THENd(總成本超支)；⑤AND施工進度是否按計劃完成c4(0)AND施工技術是否先進c3(0)，IF完工工程量結算率c1(1) THENd(總成本超支)；⑥AND施工進度是否按計劃完成c4(0)AND施工技術是否先進c3(1)，IF完工工程量結算率c1(0) THENd(總成本超支)。

研究表明，在當前的成本管理水平下該施工企業保證施工方案合理和進度按計劃完成，及時辦理完工工程結算即可達到預定的總成本控制目標。若存在某一項指標的偏差為負，均會造成總成本超支，該評價結果與權重計算保持較高的一致性。對該企業10月份成本控制決策利用以上規則集進行計算分析，結果和規則4基本相同，可見對下期成本預測利用歷史成本信息獲取的規則具有一定的可行性與科學性，在其他成本指標保持不變的條件下通過加強以上三個指標，可保證預期目標的實現。

4 結 論

1)基于粗糙集理論構建的施工成本動態控制模型揭示了成本影響因素重要程度及其偏差，在此基礎上分析了各要素對成本控制效果的作用關系，然后對各成本指標的重要性利用歷史各期成本信息進行計算分析；對當前成本控制規則采用信息系統的規則獲取和約簡算法獲取，對下期成本變化狀況進行準確預測，從而提出有效的控制策略。另外，為實現動態循環控制成本的目標，通過計算分析成本計劃值在下一個控制期內反映需要調整的目標值。

2)工程實例表明，各指標對總成本控制的貢獻率可通過該模型較好的反映，為水利工程成本控制決策和施工成本計劃實時調整提供一定參考。文章僅考慮了具有代表性的成本指標，在實踐工程中應綜合分析整個控制指標體系。另外，文章采用的離散化數據劃分刻度較為簡單，為獲取更為詳細的規則未來仍需要進一步細化刻度。