FRP鋼管混凝土柱抗爆性能數值模擬

趙均海，董 婧，張冬芳，李瑩萍

(長安大學 建筑工程學院，陜西 西安 710061)

0 引 言

鋼管混凝土作為經典的鋼管筒體內填混凝土組合結構已被廣泛研究并應用在建筑結構中。鋼管混凝土具有承載力高、塑性和韌性好及施工方便等特點[1-2]。然而在某些特定的環境下，不得不采用厚壁、大直徑的鋼管，造成工作量大、安裝工序繁瑣、成本過高等問題；同時，由于鋼管裸露在外，在某些高腐蝕性環境中采用鋼管混凝土結構就必須對鋼管進行防腐保護，從而增加養護成本。纖維增強復合材料(FRP)是由纖維材料與樹脂基體材料按一定的比例混合后形成的高性能復合材料。FRP具有比強度高、耐腐蝕等特點，已廣泛應用于工程實踐中[3-4]。近些年，一種基于鋼管混凝土的新型結構——FRP鋼管混凝土結構被提出。FRP鋼管混凝土結構即FRP復合材料與鋼管混凝土組成的復合結構，鋼管對混凝土約束的同時，FRP對鋼管混凝土整體又進行了二次加固。一方面，FRP鋼管混凝土結構可以作為一種新型結構應用于新建建筑之中；另一方面，FRP材料也可以作為修復材料用來加固既有的鋼管混凝土結構。

目前學者們對FRP鋼管混凝土構件的研究主要集中在軸壓、偏壓、抗彎等靜力性能方面[5-8]，對FRP鋼管混凝土的抗震性能、抗沖擊性能也有所涉及[9-11]，但對FRP鋼管混凝土的抗爆性能研究相對有限。Wang等[12]運用數值模擬的方式研究了FRP-混凝土-鋼管組合柱在爆炸荷載下的動力響應，并分析了FRP、鋼管厚度、混凝土強度等因素對組合柱抗爆性能的影響。該組合柱與本文研究的FRP鋼管共同約束混凝土組合柱并不完全相同。徐堅鋒[13]對爆炸荷載下的CFRP鋼管混凝土柱進行了數值模擬分析，但該模擬的荷載方式為將爆炸荷載簡化為三角形荷載，忽略了爆炸沖擊波負壓區的作用。因此，對于FRP鋼管混凝土柱抗爆性能的有效研究方法仍需要進一步探索。

結構的爆炸問題是較為典型的非線性瞬時動力學問題，運用解析方法求解爆炸力學的問題存在一定難度，運用試驗方法不僅費用高昂，而且無法體現出爆炸的過程狀態。數值模擬可以大幅度節省試驗經費，也可以觀測出很多試驗中無法得到的數據和現象。因此，在構件與結構抗爆問題的研究上，常采用數值模擬的方法[14-17]。本文采用多物質流固耦合方法建立爆炸荷載下FRP鋼管混凝土柱模型，從構件位移、應力等角度分析了FRP鋼管混凝土柱的抗爆性能。此外，還分析了FRP層數、混凝土強度等級及鋼管屈服強度對FRP鋼管混凝土柱抗爆性能的影響。

1 材料的非線性本構模型

1.1 空氣材料模型及狀態方程

空氣采用LS-DYNA中的*MAT_NULL材料模型及*EOS_LINEAR_POLYNOMIAL狀態方程，線性多項式狀態方程為

P=C0+C1μ+C2μ2+C3μ3+

(C4+C5μ+C6μ2)E

(1)

(2)

式中：P為爆轟壓力；C0～C6為狀態參數；V為相對體積；E為單位體積內能。

模擬空氣時主要參數及取值見表1。

表1 空氣材料參數

1.2 炸藥材料模型及狀態方程

炸藥采用LS-DYNA中的*MAT_HIGH_EXPLOSIVE_BURN材料模型及*EOS_JWL狀態方程，JWL狀態方程為

(3)

式中：ω，A，B，R1，R2為材料常數。

當模擬TNT炸藥時，主要參數及取值見表2。

1.3 鋼管材料模型

鋼管采用LS-DYNA中的*MAT_PLASTIC_KINEMATIC材料模型。該模型為塑性隨動強化模型，考慮了應變率影響，適合高應變率下鋼材的模擬。該材料模型建立在Cowper-Symonds模型基礎之上，其考慮應變率的屈服條件為[18]

表2 TNT材料參數

(4)

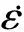
本文中鋼管材料常數取值見表3。

表3 鋼管材料參數

1.4 混凝土材料模型

混凝土采用LS-DYNA中的*MAT_JOHNSON_HOLMQUIST_CONCRETE材料模型。該模型可以應用于大應變、高應變率及高壓下混凝土材料的模擬。Johnson-Holmquist-Cook模型是Holmquist等[19]提出的一種率相關損傷型本構模型，其等效屈服強度為

(5)

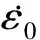
D的表達式為[20]

(6)

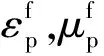
混凝土材料模型綜合考慮了混凝土大應變、高應變率以及損傷積累的影響，能夠較好地描述混凝土在爆炸、高速沖擊與侵徹下的力學行為[21]。本文中混凝土材料部分參數取值如表4所示[22]，其中，PC為壓潰點的壓力，UC為壓潰點體積應變，PL為壓實點壓力。

1.5 FRP材料模型

FRP采用線彈性材料模型。FRP布在拉斷之前可以認為一直處于彈性階段，因此可以用線彈性的應力-應變關系來模擬其本構關系[23-24]。在動力荷載作用下，材料的強度會隨著應變率的變化而改變。與鋼材、混凝土明顯的應變率效應相比，FRP的應變率效應并不明顯[25]。因此，在數值模擬中可以忽略FRP的應變率效應[26]。本文中FRP材料參數取值見表5。

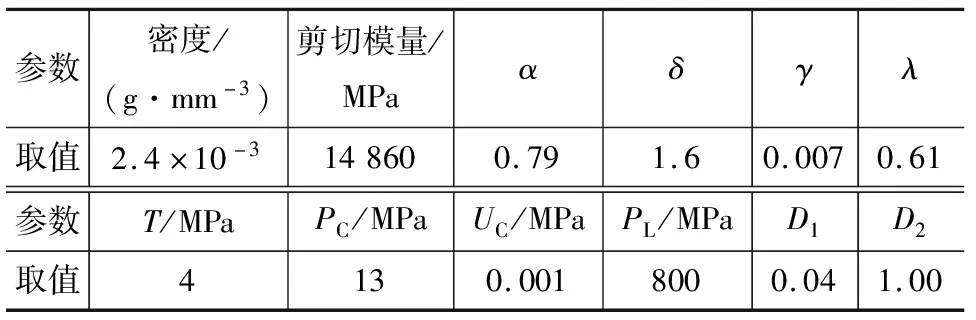
表4 混凝土材料參數

表5 FRP材料參數

2 有限元模型驗證

由于缺乏FRP鋼管混凝土柱的抗爆試驗數據，因此本文選取了筆者課題組所做的鋼管混凝土柱抗爆試驗結果進行對比驗證，視為FRP為0層時的特殊工況。此外，為了驗證FRP材料模型選擇的合理性，又建立了爆炸荷載下FRP鋼筋混凝土柱數值模型，與FRP鋼筋混凝土柱抗爆試驗進行對比驗證。

2.1 鋼管混凝土柱爆炸試驗

在中國兵器工業試驗測試研究院進行了3個圓鋼管混凝土柱的靜爆試驗[27]，鋼管混凝土柱高為1 800 mm，鋼管外直徑為273 mm，壁厚7 mm，采用Q235熱軋無縫鋼管，鋼管內澆注C40細石混凝土。本文對SC-1，SC-2試件進行數值模擬驗證。采用ANSYS/LS-DYNA軟件進行了前處理。采用125 mm×125 mm×125 mm的立方體來模擬3 kg的TNT炸藥，空氣域尺寸為2 500 mm×1 000 mm×2 500 mm。空氣域除底面添加剛性平面，其余各面采用無邊界反射條件。網格尺寸為25 mm×25 mm。炸藥、空氣、鋼管、混凝土均采用Solid實體單元。網格劃分后鋼管單元數為2 304，混凝土單元數為6 912。加入關鍵字*MAT_ADD_EROSION來判斷單元是否失效。鋼管混凝土柱兩端按固接考慮，添加位移和轉動約束。

由于SC-1試件為小藥量的爆炸試驗，試件沒有發生明顯的破壞現象，且沒有產生明顯的位移。因此，主要將SC-1柱身上6個測點的試驗數據與數值模擬數據進行對比。測點1#～6#分別設置在柱子迎爆面的柱頂、柱中、柱底與背爆面的柱頂、柱中和柱底。表6為試驗數據與數值模擬數據對比情況。由表6可知，數值模擬結果與試驗結果總體誤差較小。

表6 試驗結果與數值模擬結果對比

采用與SC-1同樣的建模方法對SC-2的爆炸試驗進行建模。采用350 mm×300 mm×300 mm的立方體來模擬50 kg的TNT炸藥，炸藥中心距柱身0.7 m。由于本次試驗為近距離大藥量爆炸試驗，試件發生了明顯破壞現象。試件在50 kgTNT炸藥近爆荷載作用下的破壞形式見圖1。通過對比可知，數值模擬結果與試驗結果接近，柱跨中都出現了明顯的變形。通過數值模擬的試件跨中位移可知，柱中最大位移為91.276 mm，而試驗結果為93 mm，相對誤差為1.85%，差異較小。驗證了該數值模型的可行性。

圖1 試件SC-2的破壞形式

2.2 FRP鋼筋混凝土柱爆炸試驗

劉路[28]對8根不同防護的鋼筋混凝土圓形墩柱進行了野外現場爆炸試驗。柱有效高度為3 500 mm，截面直徑為400 mm?；炷翉姸鹊燃墳镃40，配筋率為0.9%，縱筋為10根直徑12 mm的HRB400帶肋鋼筋，箍筋為直徑8 mm的HPB300光圓鋼筋，柱頂、柱底箍筋間距為100 mm，柱中箍筋間距為150 mm。構件JS5為外包1層FRP布的鋼筋混凝土圓柱，對該構件進行了4種不同工況下的爆炸試驗。本文對工況25，27進行模擬驗證，根據第2.1節建模方法對爆炸試驗進行建模，并將數值模擬結果與試驗結果進行對比。圖2為構件迎爆面高1 330 mm處測點超壓時程曲線對比，圖3為構件背爆面高3 300 mm處測點3#加速度時程曲線對比。由圖2，3可知，試驗數據與數值模擬數據基本吻合。

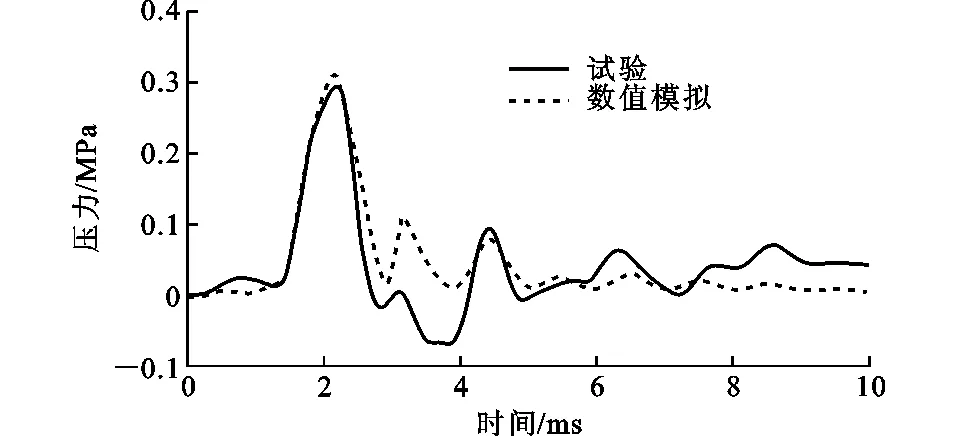
圖2 測點2#超壓時程曲線

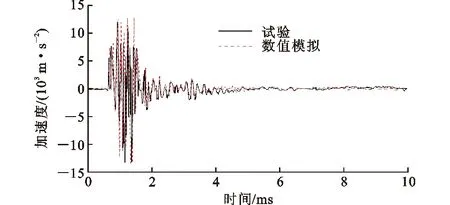
圖3 測點3#加速度時程曲線

3 FRP鋼管混凝土柱模型的建立

由前文可知材料模型的選擇和數值模型的建立都是合理的。本文采用上述模型的建立方法對典型的FRP鋼管混凝土柱進行抗爆分析。模擬構件為圓形截面鋼管混凝土柱，柱高為3 000 mm，鋼管外直徑為500 mm，核心混凝土直徑為480 mm，鋼管壁厚為10 mm，鋼管外包厚0.167 mm的FRP布，柱兩端固定約束。炸藥為300 mm×300 mm×300 mm的TNT(質量相當于44.28 kg)，炸藥中心點距離地面高1.5 m，距離構件迎爆面1 m?？諝庥虺叽鐬? 500 mm×2 000 mm×3 600 mm?？諝庥虺酌嫣砑觿傂云矫?，其余各面采用無邊界反射條件。過大的網格尺寸會使計算結果精確度降低，而過小的網格尺寸會降低計算效率，因而本文網格尺寸為25 mm×25 mm。劃分網格后FRP單元數為7 680，鋼管單元數為7 680，混凝土單元數為46 080，TNT單元數為1 728，空氣單元數為1 150 272。網格劃分后的柱截面及整體有限元模型如圖4所示。

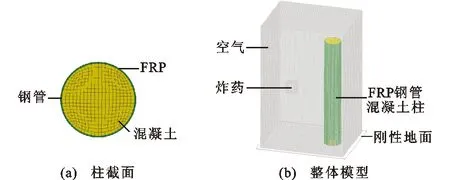
圖4 有限元模型

采用多物質流固耦合方法來模擬炸藥與結構之間的關系。使用關鍵字*SECTION_SOLID來實現FRP、鋼管、混凝土的Lagrange算法，使用關鍵字*SECTION_SOLID_ALE將炸藥和空氣定義為ALE算法。再通過關鍵字*CONSTRAINED_LAGRANGE_IN_SOLID和*ALE將流體和固體耦合在一起[29]。這種方法與共用節點和接觸耦合法相比，雖然計算量較大且計算效率偏低，但該算法網格可以在空間中流動，避免了在計算過程中網格的畸變，計算精度較高。使用關鍵字*INITIAL_DETONATION引爆炸藥。

4 數值模擬結果分析

將上述建好的模型導入LS-DYNA V971R7軟件中求解計算，隨后將結果導入后處理軟件LS-PREPOST進行分析。

4.1 FRP鋼管混凝土柱破壞形態

圖5為FRP鋼管混凝土柱的破壞形態。由圖5可以看出，柱中處產生了位移，鋼管沒有發生明顯破壞。在柱中及柱兩端處的混凝土有部分脫落，但由于外部有FRP材料與鋼管的雙重約束，因此混凝土沒有發生飛濺現象。柱整體變形情況較好，表示FRP鋼管混凝土柱有著較好的抗爆性能。

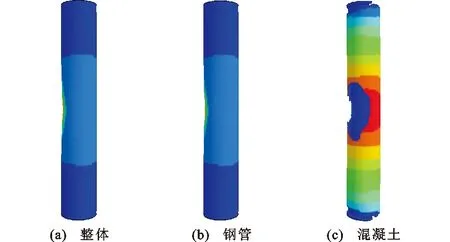
圖5 破壞形態

4.2 位 移

為研究構件在爆炸荷載作用下的位移變化，圖6給出了不同時刻FRP鋼管混凝土柱迎爆面x方向(爆炸沖擊波傳播方向)的位移云圖。從圖6可以看出，時間t=0.4 ms時，爆炸沖擊波剛抵達FRP鋼管混凝土柱，柱中位移較為明顯，達到9.924 mm。隨著時間的不斷增加，構件位移也在不斷增大。當t=0.9 ms時，柱中位移達到最大值24.13 mm。當t=2.2 ms時，柱中位移有所降低，上下兩端處位移有所增加。位移在整體上呈現中部大、兩端小的對稱分布形式。

圖7為FRP鋼管混凝土柱中點在爆炸荷載作用下位移時程曲線。從圖7可以看出，在爆炸開始后的0～0.2 ms內，FRP鋼管混凝土柱并未發生橫向(x軸方向)位移。這段時間為空氣中的炸藥起爆后沖擊波在空氣中的傳播時間。0.2 ms后，FRP鋼管混凝土柱中部沿爆炸沖擊波傳播方向(x軸正方向)位移迅速增加，在0.9 ms時達到最大，最大橫向位移為24.13 mm。隨后FRP鋼管混凝土柱的橫向位移逐漸減小，并在12 mm左右振動。

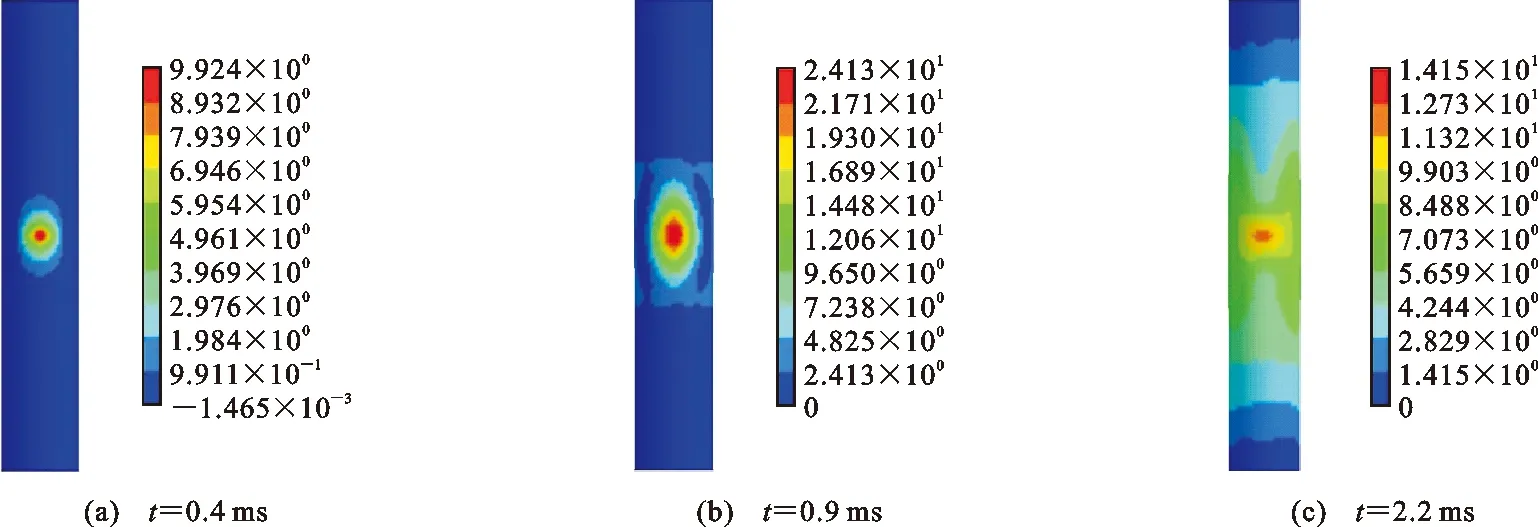
圖6 迎爆面不同時刻位移云圖(單位:mm)

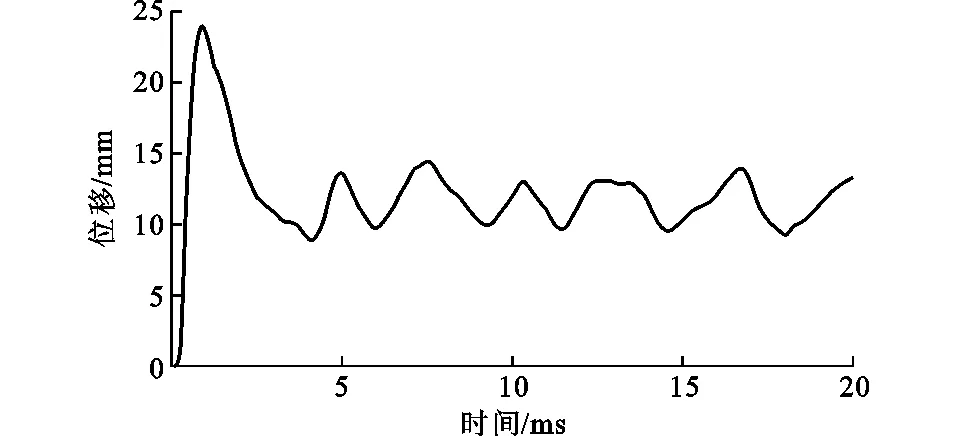
圖7 柱中位移時程曲線

4.3 鋼管等效應力

爆炸沖擊荷載下FRP鋼管混凝土柱的應力狀態是十分復雜的，通常采用等效應力來表示其應力特征。圖8給出了不同時刻鋼管迎爆面等效應力云圖。

從圖8可知，在0.3 ms時，柱中應力迅速增大。柱中峰值應力達到了410.93 MPa，超過了鋼管的靜態屈服強度。隨著時間的推移，應力較大的區域逐漸由柱中逐漸向柱的兩端延伸。在1.6 ms時，柱中及柱兩端大部分單元應力都在294～364 MPa之間，超出了鋼管的靜態屈服強度。柱中與柱頂、柱底之間的過渡區應力相對較小，沒有超過鋼管的靜態屈服強度。在3 ms時，柱中及柱兩端應力開始減小。等效應力總體上呈現上下對稱分布。由此可見，爆炸荷載作用下的FRP鋼管混凝土柱易受到損傷的部位為柱中及柱兩端。

4.4 混凝土等效應力

圖9給出了不同時刻混凝土側面的等效應力云圖。從圖9可以看出，與鋼管的等效應力相比，混凝土的等效應力沿構件縱向分布比較均勻。在初始階段，混凝土柱中等效應力迅速增大，柱中峰值處達到了150 MPa，超過了混凝土靜態極限應力。其他區域等效應力偏小，沒有超過混凝土靜態極限應力。由于模擬時添加了EROSION關鍵字，當混凝土單元拉伸應變值超過設定的失效應變0.001時，該單元會被刪除[30]。隨著時間的推移，混凝土柱中部分單元先退出工作；柱頂、柱底處應力增大，此處單元隨后退出工作，發生剪切破壞。背爆面柱中處應力逐漸增大，部分單元的等效應力值在47～56 MPa之間，超過了混凝土靜態極限應力。由此可知，在迎爆面柱中和柱兩端以及背爆面柱中的混凝土等效應力值偏大，上述區域也為混凝土在爆炸荷載下的易損區域。

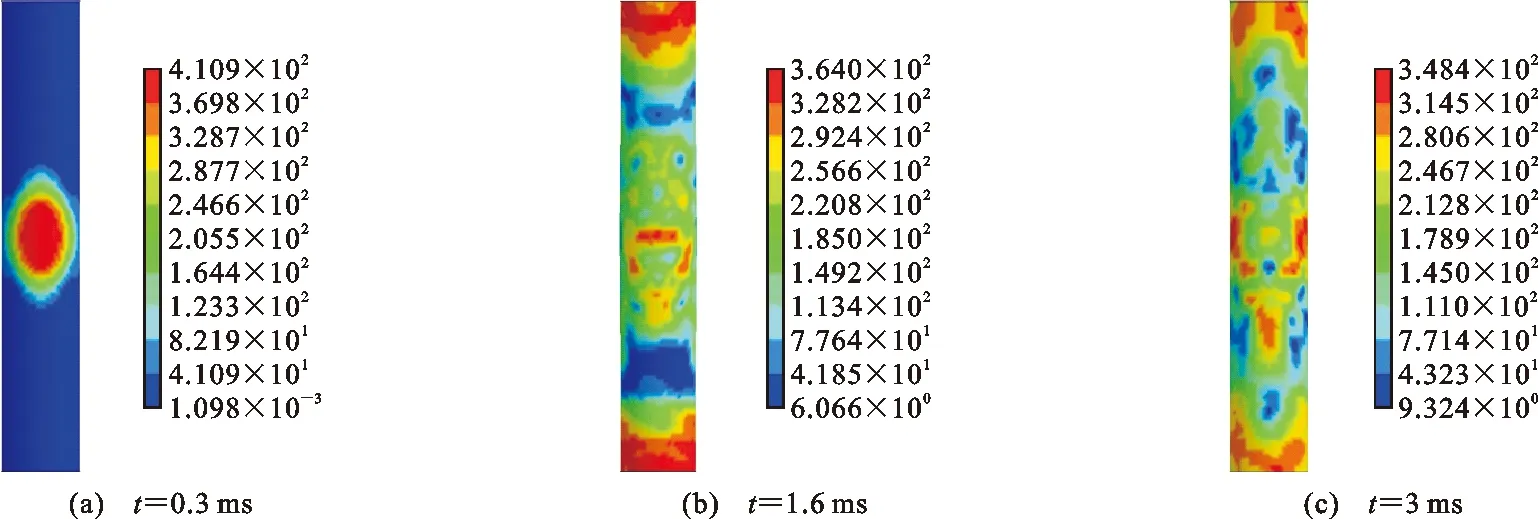
圖8 迎爆面不同時刻鋼管等效應力(單位:MPa)

圖9 側面不同時刻混凝土等效應力(單位:MPa)

4.5 FRP等效應力

圖10給出了FRP鋼管混凝土在爆炸荷載作用下FRP的等效應力云圖。由圖10可知，FRP的應力分布與鋼管應力分布類似。應力較大的區域仍為柱中區域。隨著時間的推移，柱兩端處應力逐漸增大。形成柱中及柱兩端應力較大，柱中至柱頂、柱底過渡區應力較小的分布狀態。

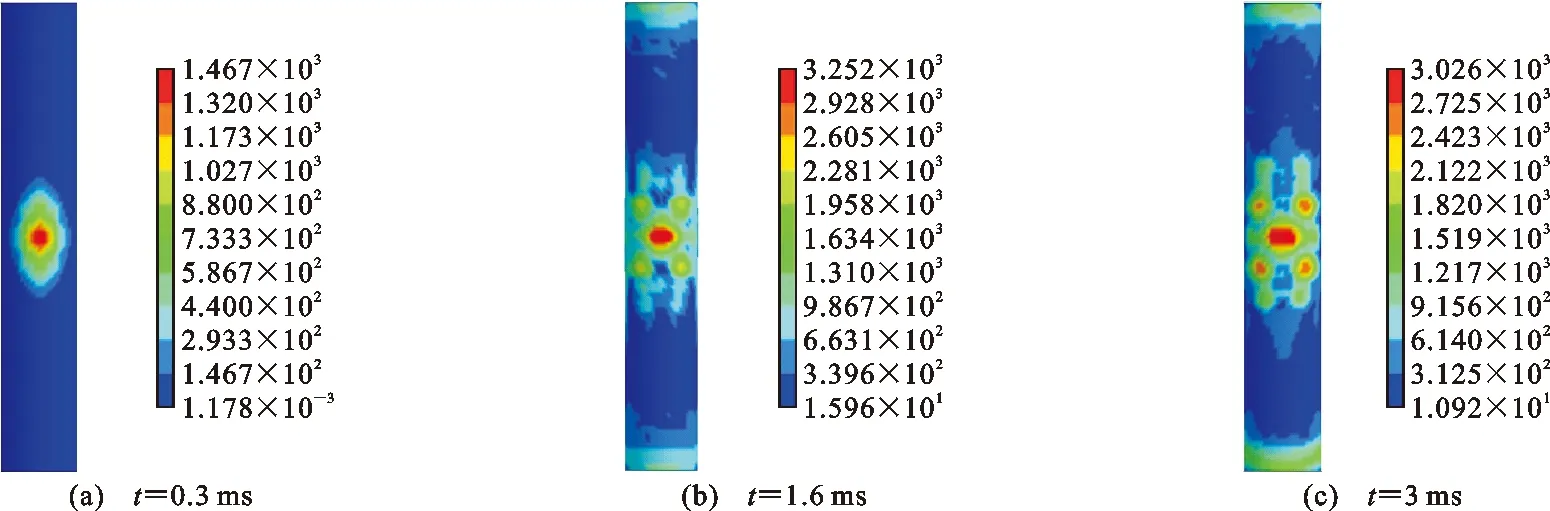
圖10 迎爆面不同時刻FRP等效應力(單位:MPa)

5 參數分析

5.1 FRP層數

為了研究FRP層數變化對FRP鋼管混凝土柱抗爆性能的影響，在保持其他材料參數不變的條件下，通過改變FRP的厚度來對爆炸荷載作用下不同層數的FRP鋼管混凝土柱動力響應進行模擬分析。

圖11給出了當FRP為0～4層(FRP厚度分別為0，0.167，0.334，0.501，0.668 mm)時FRP鋼管混凝土柱的柱中位移時程曲線。從圖11可以看出：當FRP為0層時，即無FRP約束的鋼管混凝土柱在爆炸荷載作用下柱中最大位移為30.17 mm；當FRP為1層時，FRP鋼管混凝土柱中最大位移為24.13 mm，與未加固的鋼管混凝土柱相比，位移減少了6.04 mm，由此可知FRP的約束可以有效地提高鋼管混凝土柱的抗爆性能；當FRP為2～4層時，柱中最大位移分別為22.11，19.52，19.37 mm。這說明隨著FRP層數的增加，柱的抗爆性能也得到進一步提升，但FRP層數對柱抗爆性能的影響逐漸減弱。3層FRP與4層FRP的柱中位移已經比較接近，但顯然3層要比4層更為經濟。

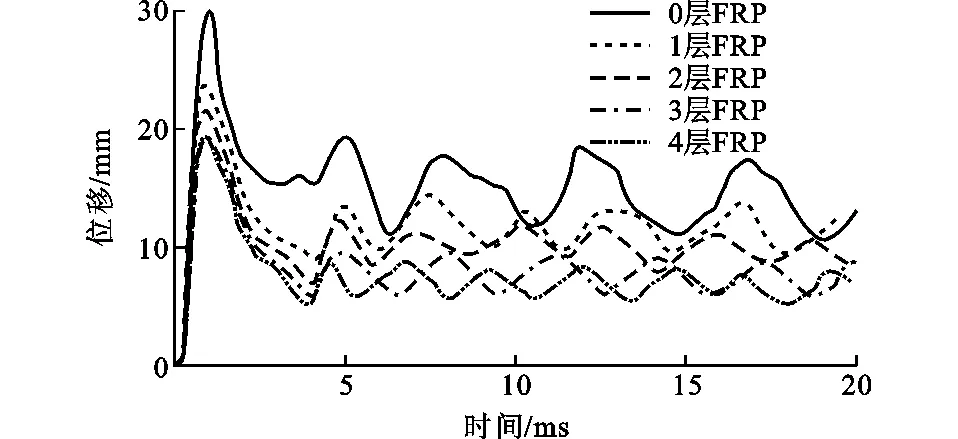
圖11 不同FRP層數柱中位移時程曲線

5.2 混凝土強度等級

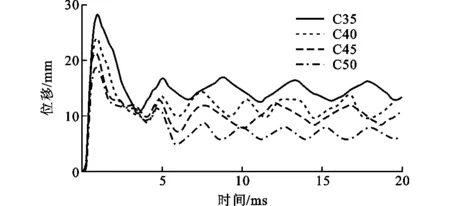
圖12 不同混凝土強度等級柱中位移時程曲線

為了研究不同強度等級的混凝土對FRP鋼管混凝土柱抗爆性能的影響，保持其他參數不變，對4種混凝土強度等級不同的FRP鋼管混凝土柱在同一爆炸荷載下的動力響應進行分析。圖12為這4種柱的柱中位移時程曲線。由圖12可知，當混凝土強度等級為C35，C40，C45，C50時，FRP鋼管混凝土柱中最大位移分別為28.32，24.13，21.65，18.90 mm。隨混凝土強度等級的提高，FRP鋼管混凝土柱中最大位移逐漸減小。這說明提高混凝土強度可以提高FRP鋼管混凝土柱的抗爆性能。

5.3 鋼材屈服強度

圖13 不同鋼管屈服強度柱中位移時程曲線

為研究鋼材屈服強度對FRP鋼管混凝土柱抗爆性能的影響，保持其他參數不變，對4種不同屈服強度鋼材的FRP鋼管混凝土柱進行抗爆分析。柱中位移時程曲線如圖13所示。由圖13可知，當鋼管屈服強度為Q235，Q345，Q390，Q430時，FRP鋼管混凝土最大位移分別為24.13，22.45，21.80，20.64 mm。隨著鋼管屈服強度的提高，由爆炸荷載所致的構件位移也隨之減小，但減小的幅度也相應降低。這說明提高鋼管的屈服強度可以提高FRP鋼管混凝土柱的抗爆性能，但影響程度不大。

6 結語

(1)鋼材采用塑性隨動強化模型，混凝土采用Johnson-Holmquist-Cook模型，FRP采用線彈性模型，運用ALE流固耦合方法建立了爆炸荷載作用下FRP鋼管混凝土數值模型。模型計算結果與試驗數據進行對比，驗證了數值模型的合理性。該模型可以進一步推廣到分析不同截面、不同比例距離下FRP鋼管混凝土構件的抗爆性能，為該類構件的抗爆設計與防護提供了一定依據。

(2)在爆炸荷載作用下，構件沿爆炸沖擊波傳播方向產生位移。位移在短時間內迅速達到峰值，隨即下降到某一個范圍內振動。位移整體上呈現柱中偏大、兩端偏小的分布。鋼管、混凝土、FRP的應力總體呈現出對稱型分布狀態。柱中及柱兩端應力偏大，柱中至柱兩端之間過渡區域應力偏小。爆炸荷載作用下FRP鋼管混凝土柱易受損部位為柱中及柱兩端。

(3)FRP的約束提高了鋼管混凝土柱的側向剛度和承載能力。FRP層數越多，構件的抗爆性能越好，但隨著層數的增多，FRP對構件抗爆性能的影響變小。因此，FRP的最優且最經濟的層數有待進一步研究。此外，提升混凝土強度及鋼管屈服強度均可以提高FRP鋼管混凝土柱的抗爆性能。