慣性/星光制導誤差分離的可觀測度研究

郭振西，武 斌，謝 佳，閔昌萬

慣性/星光制導誤差分離的可觀測度研究

郭振西，武 斌，謝 佳，閔昌萬

（空間物理重點實驗室，北京，100076）

基于捷聯慣性測量組合和星敏感器的“慣性+星光”復合導航方式綜合了兩種導航方式的優點，可以實現組合導航的高動態和高精度。研究了慣性/星光組合制導捷聯安裝的系統誤差模型及其可觀測度分析方法，計算了在不同位置進行誤差分離的系統狀態可觀測度，并通過數學仿真證明了該分析方法的有效性，可應用于慣性/星光制導方案在線分離慣性失準角和安裝誤差角的方案快速論證。

捷聯星光制導；誤差分離；可觀測度

0 引 言

“慣性+星光”復合導航方式取兩種導航方式的優點而互補其短，既利用慣性器件全程自主地提供姿態信息，又利用星光在中段對慣性導航的誤差進行修正，達到精確導航的目的[1]。為克服系統運動模型的非線性，現代捷聯慣性/星光制導多采用擴展卡爾曼濾波（Extended Kalman Filter，EKF）、無損卡爾曼濾波（Unscented Kalman Filter，UKF）、粒子濾波（Particle Filter，PF）等濾波方法進行組合導航[2~8]。一般而言，對于機動發射平臺而言，受載機運動和機體變形的影響，子慣導的初始失準角特別是方位失準角誤差較大。為了保證自主制導的精度，可在飛行過程中采用“慣性+星光”的模式對初始方位失準角進行修正。有些飛行器受到安裝空間的限制，星敏和慣組不能安裝在同一個剛性支架上。受運輸環境和飛行過程的影響，在觀星時刻，星敏和慣組會產生一定的安裝角誤差，本文通過分析星敏和慣組之間的輸出信息和誤差激勵模型，通過飛行器在觀星時刻的簡單滾轉，在線分離安裝誤差，修正慣性導航系統的方位失準角。利用觀測矩陣的奇異值分解計算分析不同誤差狀態的可觀測度，為飛行過程的姿態角激勵時序提供依據，最終保證慣性自主制導系統的誤差修正精度。

1 慣性導航和星敏感器建模

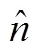
1.1 雙視場星敏誤差模型

雙視場星敏感器一次觀星可以測得慣性系的基準。對于與飛行器捷聯安裝而言，確定慣性基準的具體方法如下（星敏感坐標系和飛行器坐標系重合）：

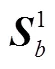
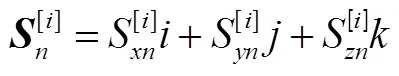
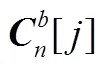
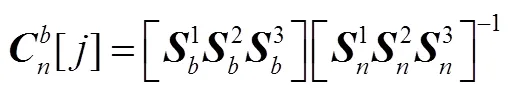
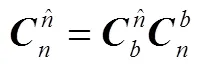
1.2 慣組誤差模型

慣性星光組合制導主要包括兩個誤差源：計算慣性系誤差（導航系誤差）和星敏感器安裝誤差。對于采用高精度慣導系統的“慣組+星光”組合制導系統，將不同觀星時刻的陀螺漂移和星敏觀星誤差看作噪聲。

a）定義導航系誤差：

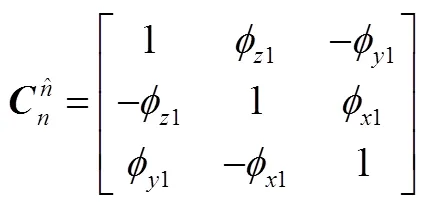
b）星敏感器安裝誤差：

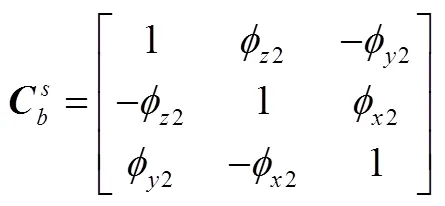
c）第次觀星的結果：

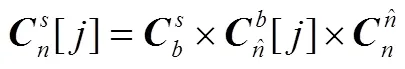
式（6）中，將方向余弦矩陣替換為對應的四元數算法[7]：

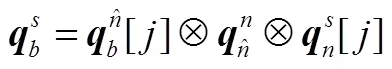
由式（4）~（7）得：

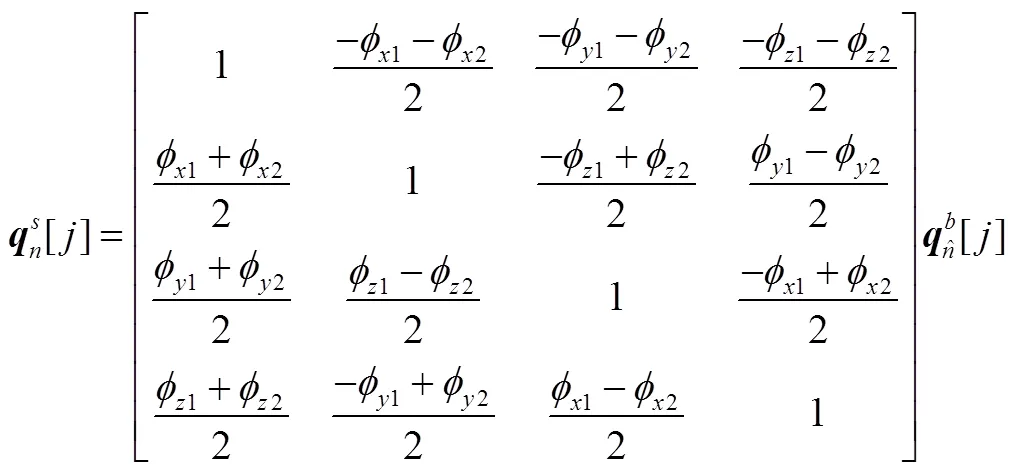
寫成矩陣形式：

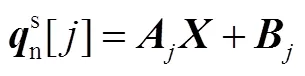
式中

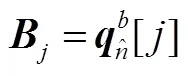
式（9）即一次觀星所得到的觀測量和系統狀態之間的關系。

2 星光制導的系統可觀測度

根據式（9）如果有多次觀測則可以列出一個方程組為

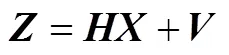
得到的最小二乘觀測結果和協方差矩陣為[8]

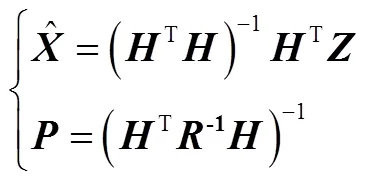
式中為星敏測量結果；為待估計的失準角；為觀測矩陣；為星敏感器觀測四元數的噪聲方差；且

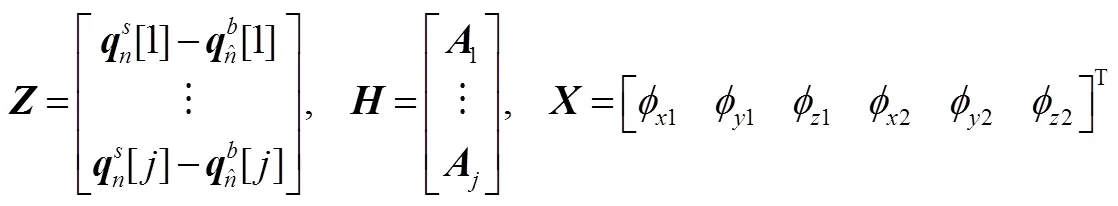
如果通過陣的特征值判斷失準角估計結果受調姿矩陣的影響，則陣特征值反映了失準角估計誤差的協方差。

如果系統的可觀測度足夠大，即陣不奇異，可以通過最小二乘法分離出6個誤差項，即3個星敏安裝誤差角和3個慣組失準角。計算不同狀態下的矩陣的奇異值和其所對應的奇異值分解向量，可以反映不同觀星方式下的系統可觀測度。本文采用系統觀測矩陣的最小非0奇異值表征可觀測狀態的可觀測度。

2.1 一次觀星可觀測度

對雙視場星敏一次觀星的觀測矩陣進行奇異值分解：

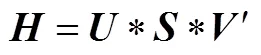
得到：

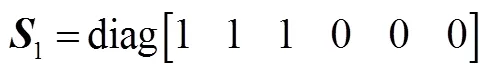
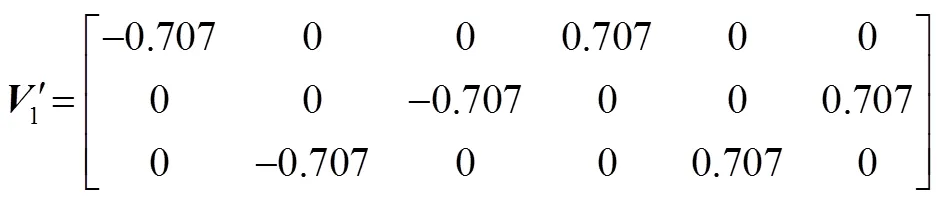
2.2 兩次觀星可觀測度

星敏兩次觀星，分別繞慣性系旋轉角度為30°、45°、60°，得到：

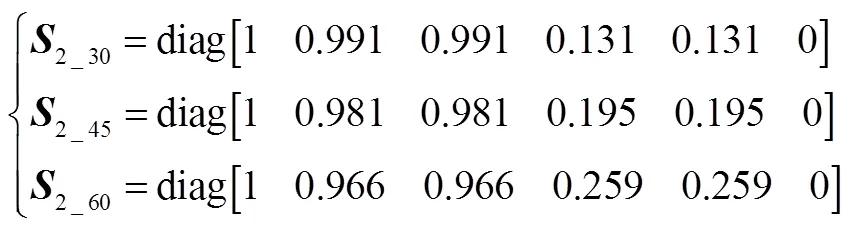
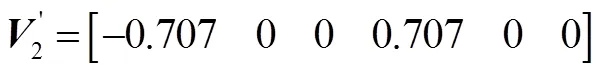
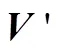
2.3 三次觀星的可觀測度

星敏3次觀星，分別繞慣性系和旋轉30°，得到：

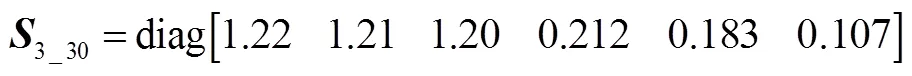
矩陣的秩為6，無0奇異值，所有狀態可觀，全部失準角和安裝誤差角可分離。不同觀星狀態下觀測矩陣的可觀測度如表1所示。

表1 不同觀星情況下的觀測矩陣的可觀測度

Tab.1 System Observability under Different Stargazing Conditions

觀星情況1次觀星*2次觀星（繞慣性系X軸旋轉）3次觀星 觀星狀態不旋轉旋轉30°旋轉45°旋轉60°分別繞X、Y旋轉30° H矩陣秩356 奇異值最小值10.1310.1950.2590.107 系統可觀測狀態√×××√ √√√√√ √√√√√ ××××√ ×√√√√ ×√√√√

注：*一次觀星的可觀測狀態，是指沒有安裝誤差角時，3個失準角可觀

根據上面的分析，可以得到以下結論：

a）在沒有安裝誤差的情況下，一次觀星可以測得三軸失準角；

b）兩次觀星總有一個方向的安裝誤差角和失準角不可觀，即所繞軸的失準角和安裝誤差角不可觀，而與轉動方向垂直的安裝誤差角和方位失準角可分離。

c）兩次觀星繞一個軸的轉動角度越大，系統的可觀測度越大。

d）兩次不同軸（慣性空間不同軸）轉動可以測得全部3個失準角，并分離3個方向的安裝誤差角。

3 誤差分離數學仿真

星敏感器兩次測星所需的飛行器姿態（可根據需求，如盡可能調姿較小，優先使用滾轉角等），生成星光調姿諸元進行裝訂。根據兩次測星識別結果，分離星敏感器與慣組安裝誤差，同時修正飛行器方位向失準角，完成星光制導。取星敏感器測量誤差為2"（1），慣組陀螺漂移2"（1），進行1000次打靶仿真，滾轉方向兩次測星的角度為30°，得到仿真結果如圖1所示。

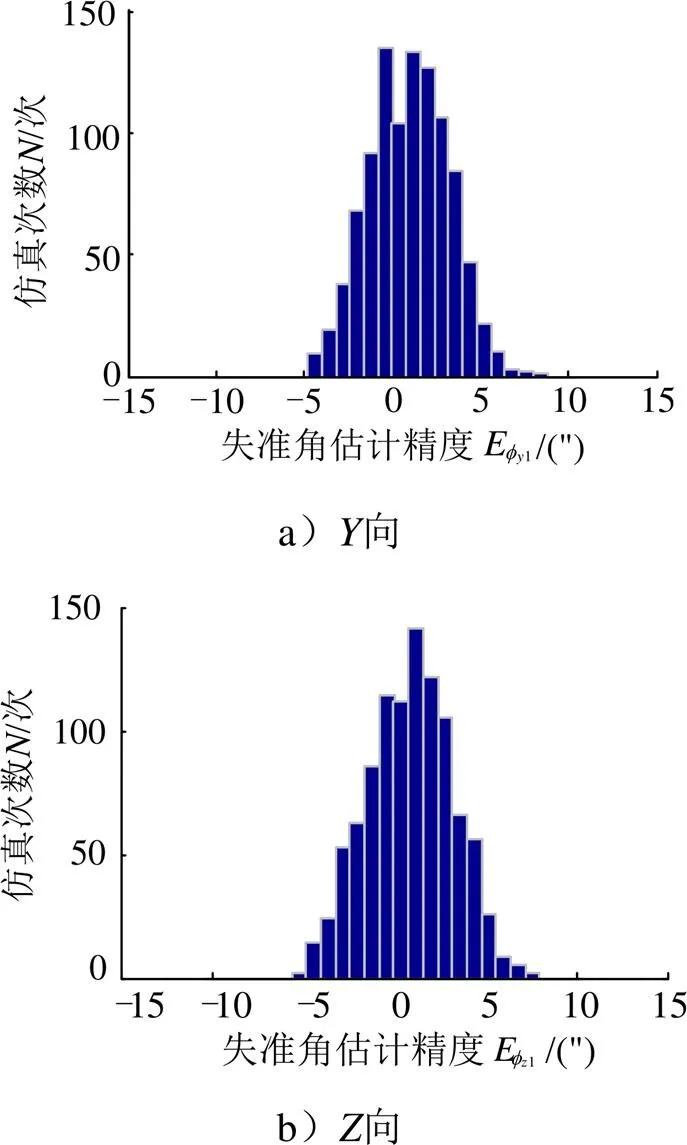
圖1 繞X軸兩次觀星誤差分離仿真結果

4 結 論

通過對“慣性+星光”復合制導的誤差模型觀測矩陣的奇異值分解，結合奇異值所對應的系統狀態變量，可快速定量地計算出不同機動模式下的系統狀態可觀測度。結果表明：

a）兩次觀星總有一個方向的安裝誤差角和失準角不可觀，即所繞軸的失準角和安裝誤差角不可觀，而與轉動方向垂直的安裝誤差角和方位失準角可分離。

b）兩次觀星繞一個軸的轉動角度越大，系統的可觀測度越大。

c）兩次不同軸（慣性空間不同軸）轉動可以測得全部3個失準角，并分離3個方向的安裝誤差角。

對于大視場星敏感器，在飛行器姿態角調整受限情況下，也可以參照這一結論制定相應誤差分離調姿方案。

[1] 賈大玲, 李連仲, 嚴衛鋼. 基于星敏感器的彈載陀螺工具誤差分離研究[J]. 計算機仿真, 2002, 23(2): 40-43.

Jia Daling, Li Lianzhong, Yan Weigang. Missile borne gyroscope error separation based on star-sensor[J]. Computer Simulation, 2006, 23(2): 40-43.

[2] 趙長山, 秦永元, 夏家和. SINS/星敏感器組合導航方案研究[J]. 西北工業大學學報, 2008, 26(5): 631-634.

Zhao Changshan, Qin Yongyuan, Xia Jiahe. Improving online autonomous calibration of SINS/Star sensor integrated system[J]. Journal of Northwestern Polytechnical University, 2008, 26(5): 631-634.

[3] 敖宏奎, 等. INS/GNSS/CNS組合導航系統仿真研究[J]. 彈箭與制導學報, 2007, 27(4): 78-80.

Ao Hongkui, et al. Simulation of INS/GNSS/CNS integrated navigation[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2007, 27(4): 78-80.

[4] 羅楠, 許錄平, 張華. 基于UKF和信息融合的航天器自主導航方法[J]. 中國空間科學技術, 2012, 4(2): 1-8.

Luo nan, Xu Luping Zhang Hua. Method of autonomous celestial navigation based on UKF and information fusion[J]. Chinese Space Science and Technology, 2012, 4(2): 1-8.

[5] Yin Jianjun, Zhang Jianqiu, Mike Klass. The marginalized rao-blackwellized particle filter for mixed linear/nonlinear state space models[J]. Chinese Journal of Aeronautics, 2007, 20(4): 346-352.

[6] 羅寧, 周磊, 張銳, 樊建文. 基于星敏感器的天文/慣導組合導航仿真研究[J]. 現代導航, 2014, 5: 342-346.

Luo Ning, Zhou Lei, Zhang Rui, Fan Jianwen. Research on CNS/SINS integrated navigation by simulation[J]. Modern Navigation, 2014(5): 342-346.

[7] 秦永元. 慣性導航[M]. 北京: 科學出版社, 2006.

Qin Yongyuan. Inertial Navigation System[M]. Beijing: Science Press, 2006: 288-292.

[8] 秦永元, 張洪鉞, 汪淑華. 卡爾曼濾波和組合導航系統[M]. 西安: 西北工業大學出版社, 2015.

Qin Yongyuan, Zhang Hongyue, Wang Shuhua. Theory of Kalman filter and integrated navigation system[M]. Xi’an: Northwestern Polytechnical University Press, 2015.

Study on the Observability of INS/CNS Guidance Error Separation

Guo Zhen-xi, Wu Bin, Xie Jia, Min Chang-wan

(Science and Technology on Space Physics Laboratory,? Beijing, 100076)

The combined navigation system of INS (Inertial Navigation System)/CNS (Celestial Navigation System) is studied. The system error model of INS/CNS based on the strapdown INS installation approach is firstly developed. Then, the observability analysis method of the system error model is investigated, upon which the different observability of error separation at different locations is calculated. Finally, the effectiveness of the proposed analysis method is proved by numerical simulation. The above findings can be well applied to the inertial/starlight guidance scheme to quickly separate the inertial misalignment angle and the installation error angle, and finally achieve the high dynamics and precision.

strapdown starlight guidance; error separation; observability

V448

A

1004-7182(2020)02-0054-04

10.7654/j.issn.1004-7182.20200211

郭振西（1976-），男，研究員，主要研究方向為飛行器導航制導技術。

武 斌（1984-），女，高級工程師，主要研究方向為飛行器導航制導技術。

謝 佳（1985-），女，高級工程師，主要研究方向為飛行器導航制導技術。

閔昌萬（1971-），男，研究員，主要研究方向為飛行器總體設計。

2018-10-31；

2019-02-21