考慮結構整體特性的鋼筋混凝土框架震后殘余側移響應研究

韓建平 高 珺 孫小云 拜立崗

（1.蘭州理工大學甘肅省土木工程防災減災重點實驗室，蘭州730050；2.蘭州理工大學防震減災研究所，蘭州730050；3.同濟大學土木工程學院，上海210092）

0 引 言

基于不同地震激勵水平下的結構分析結果進行抗震性能評估是基于性能地震工程的主要研究內 容 之 一［1］。 目 前 采 用 的 工 程 需 求 參 數（Engineering Demand Parameters，EDPs）以基于地震作用下的瞬時響應或累積能量耗散為主，特別是結構整體水平和構件水平的最大位移響應和其自身的延性能力。對歷次災害進行理論和調查研究結果均表明，結構體系經歷地震作用之后，殘余變形對結構體系損傷評價和性能評估有不可忽視的作用，可以考慮將其視為常見結構體系損傷和性能評價的補充指標［2-3］。

1995 年日本在經歷阪神地震后，調查研究表明有超過100 根鋼筋混凝土柱由于殘余層間側移角大于1.5%，雖然在地震中未發生倒塌但無法繼續使用導致不得不拆除［4］。此后，各國開始將結構殘余變形作為抗震中的問題之一進行研究，《日本公路橋梁設計規程第V部分:抗震設計》提出了橋墩震后殘余位移限值的規定［5］。McCormick 等對日本東京大學一幢既有建筑進行研究，結果表明:當建筑的殘余側移角達到0.5%時，住戶就會有感知；大于0.5%，則住戶就有眩暈和惡心的感覺［6］。Kawashima 等提出了殘余位移反應譜的概念［4］。Christopoulos［2-3］分別對單自由度（SDOF）和多自由度（MDOF）體系進行研究，發現分析時采用不同的滯回特性、非彈性機理以及地震動強度指標等，對結構殘余位移響應影響較大，同時提出高階振型和P-Δ效應對結構殘余位移的影響不容忽視，通過聯合使用最大位移角和殘余位移角建立性能指標矩陣，從而定義結構體系的總體性能水平。Ruiz-Garcia 等的研究表明，鋼框架殘余位移的大小與分布對地震動烈度、結構層數、自振周期、框架機制以及模型所采用不同的滯回特性等都很敏感，并且強調了對殘余位移估計時的不確定性［7］。Yazgan 對殘余位移響應的可靠預測以及所需的恰當數值模型做了深入的研究，通過對比試驗結果，提出了基于概率的、考慮殘余變形的震后損傷評估方法［8］。Hatzigeorgiou 等基于SDOF體系的不同影響參數，推導出一個簡潔、可靠的經驗方程，旨在根據地震作用下的體系殘余變形估算出體系最大變形［9］。

目前，殘余位移這一指標的研究在我國主要集中于SDOF 體系。歐陽承新等研究了對不同結構參數，如阻尼比、自振周期、采用不同滯回特性等的SDOF 體系，輸入地震動記錄后研究體系殘余位移［10］。葉列平等研究發現，屈服后剛度系數γ越大，結構殘余位移越小［11］。郝建兵等研究了雙線性SDOF 體系在不同強度折減系數和屈服后剛度系數情況下，體系殘余位移與地震動強度指標之間的相關性，建議在計算體系殘余位移時，以PGV強度指標作為地震動記錄的主要指標［12］。余波等通過對橋梁結構進行大量非彈性動力分析，并對SDOF 體系定量分析了P-Δ效應、規一化屈服強度等結構殘余位移的概率統計特征影響，結果表明殘余位移與峰值位移之間的相關性［13］。

本文通過對3 個樓層數不同的多高層鋼筋混凝土框架結構進行靜力推覆分析，將3 個結構的pushover 曲線簡化成三線性，從而得到結構整體性特性指標如屈服后剛度比和下降段剛度比，進而對3 個結構分別進行3 個強度水平、22 條地震動記錄下的彈塑性時程分析，計算得到最大層間位移角和最大殘余層間位移角的平均值、標準差和變異系數，并對結構整體特性如結構基本自振周期、屈服后剛度比、下降段剛度比等對最大層間位移角和最大殘余層間位移角的影響和最大層間位移角與最大殘余層間位移角之間的相關性進行了分析討論。

1 結構模型和地震動選擇與調整

1.1 結構概況與分析建模

首先依據我國現行《建筑抗震設計規范》（GB 50011—2010）［14］進行抗震設計，采用 PKPM系列軟件對圖1所示5層、8層和11層鋼筋混凝土框架結構公寓樓進行建模分析計算。3 個結構所在地抗震設防烈度為8 度，設計基本地震加速度為0.20g，設計地震分組為第三組，Ⅱ類場地。混凝土強度等級均采用C35，受力主筋采用HRB400鋼筋，箍筋采用HPB300 鋼筋。不上人屋面，屋面活荷載標準值為0.5 kN/m2，樓面活荷載標準值為走廊2.5 kN/m2、其他部分2.0 kN/m2。第1 層層高為3.9 m，其余各層層高均為3.6 m，5 層、8層和11 層結構的總高度分別為18.3 m、29.1 m 和39.9 m。

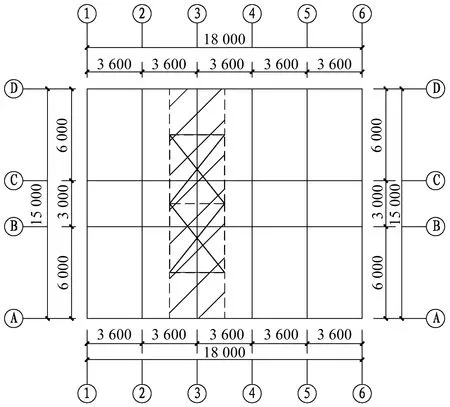
圖1 鋼筋混凝土框架平面布置圖（單位:mm）Fig.1 Floor plane of RC frame structure（Unit:mm）

根據圖1 所示的結構平面布置圖，取圖中陰影部分即一榀橫向框架作為計算單元。以5 層框架結構為例，其結構計算簡圖及配筋如圖2 所示，利用OpenSees 有限元軟件進行建模分析。采用中心線模型，以基于材料本構關系的纖維單元作為非線性分析模型，混凝土本構關系模型采用考慮抗拉的Concrete02，鋼筋本構關系模型采用可考慮強度退化的ReinforcingSteel，梁柱單元均采用基于位移的梁柱單元（Displacement-Based Beam-Column Element），每個柱單元設置 5 個積分點。幾何坐標轉換選用P-Delta 轉換（P-Delta Transformation），即考慮結構的P-Δ效應，樓板平面采用完全剛性假定。

1.2 地震動記錄選擇與調整

1.2.1 地震動記錄選擇

影響結構響應的地震動特性主要有幅值、頻譜特性和持時。以2010 規范設計反應譜為目標譜，基于譜匹配方法從太平洋地震工程研究中心（PEER）地震記錄數據庫中選取22 條地震動記錄，選擇重要持時Ds（Significant Duration）作為強震持時［15-16］。為了避免重要持時變動過大，所選地震動記錄的重要持時處于10～40 s。選取的地震動記錄如表1所示。

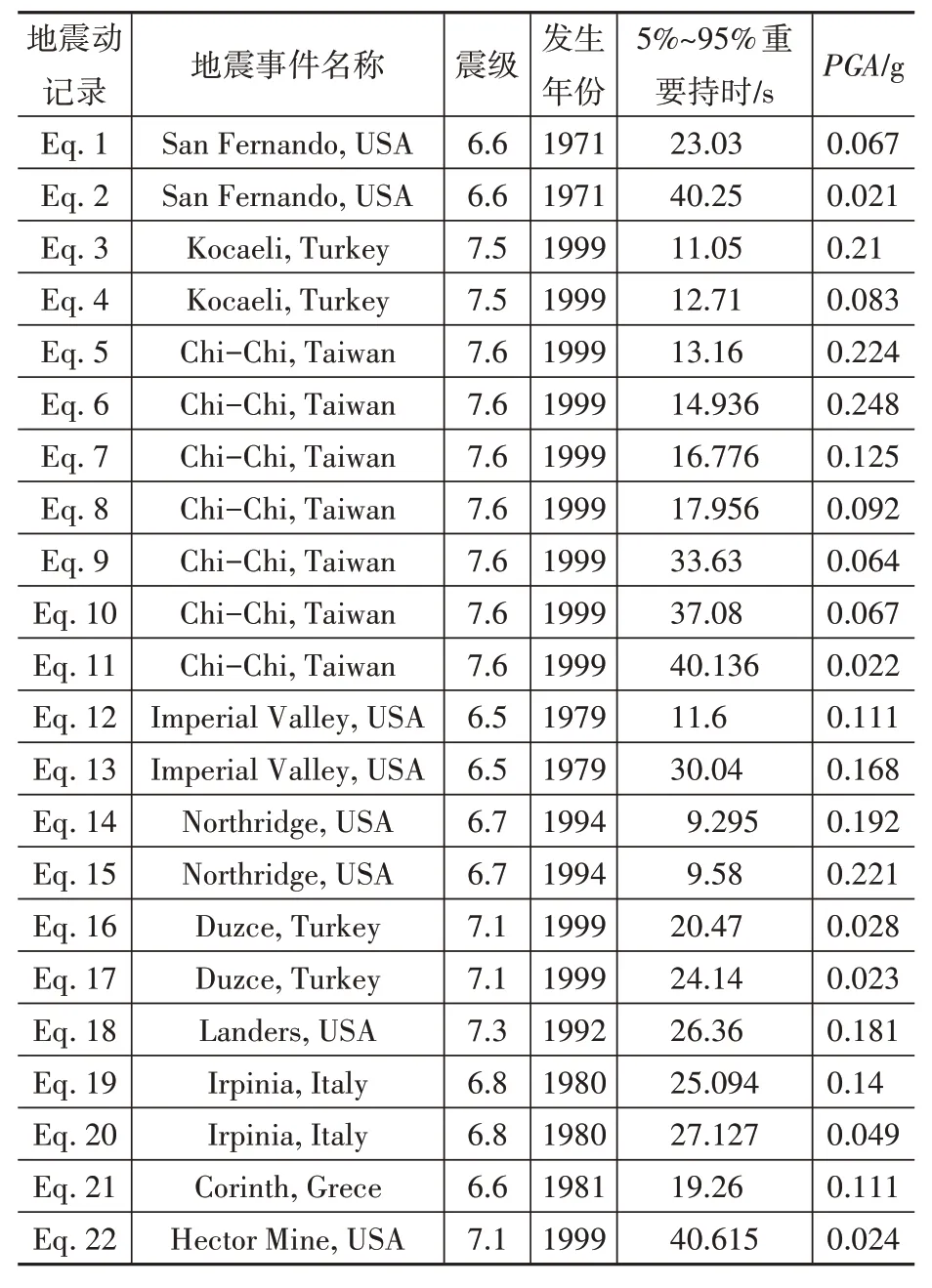
表1 選取的地震動記錄Table 1 Selected ground motion records

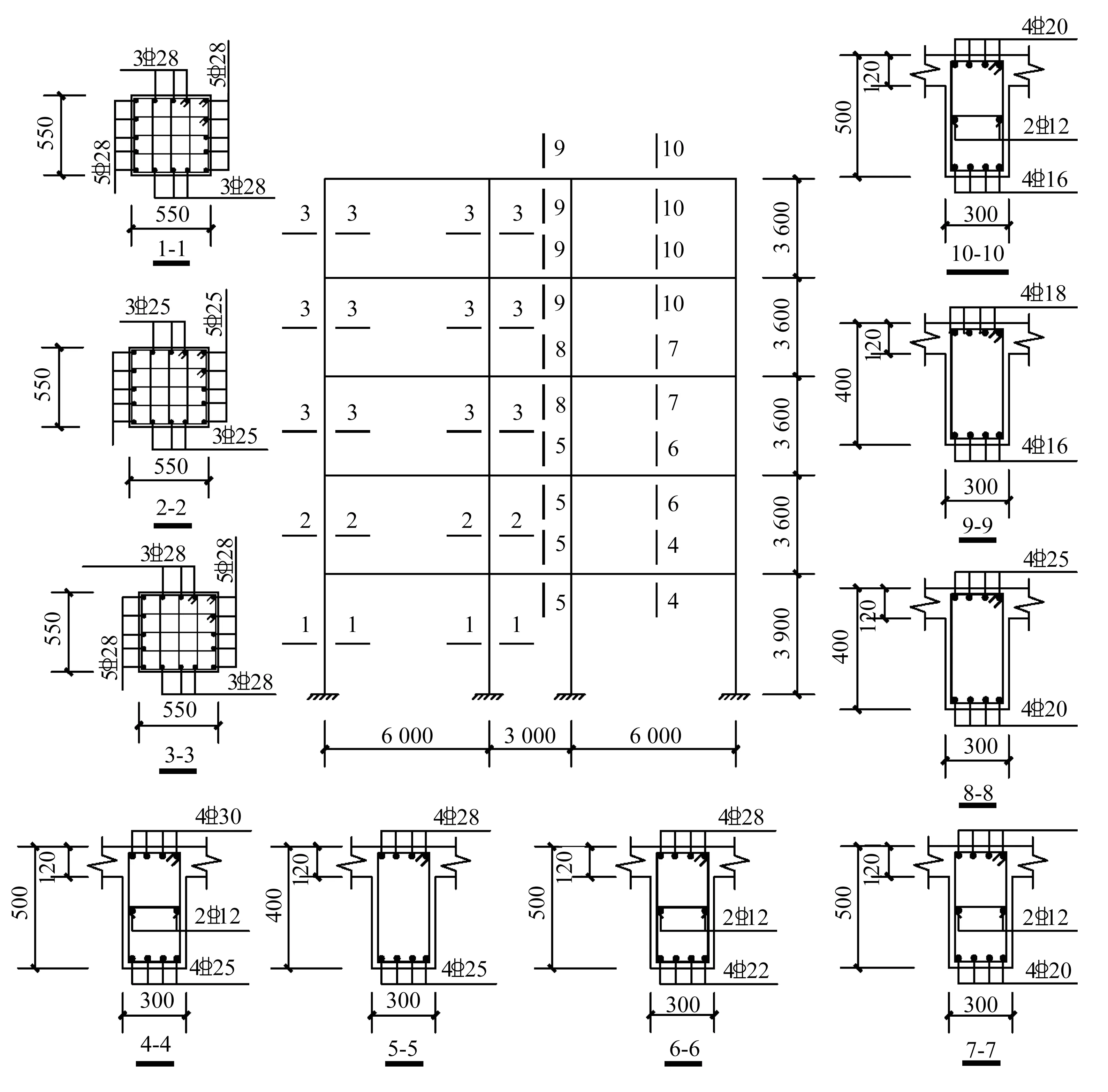
圖2 5層鋼筋混凝土平面框架結構模型Fig.2 Structural model of 5-story RC planar frame structure

1.2.2 地震動記錄調整

與規范譜匹配前后的地震動記錄的加速度反應譜分別如圖3（a）和圖3（b）所示。以匹配后的平均加速度反應譜平臺段的譜值A 作為地震動強度指標，為了研究不同地震動記錄強度水平下3 個結構模型的地震響應的大小和分布，將選取的地震動記錄分別調整到水平1（A=0.9g）、水平 2（A=1.2g）和水平 3（A=1.4g），分別對應 8 度（0.2g）、8度（0.3g）和9度的罕遇地震水準。

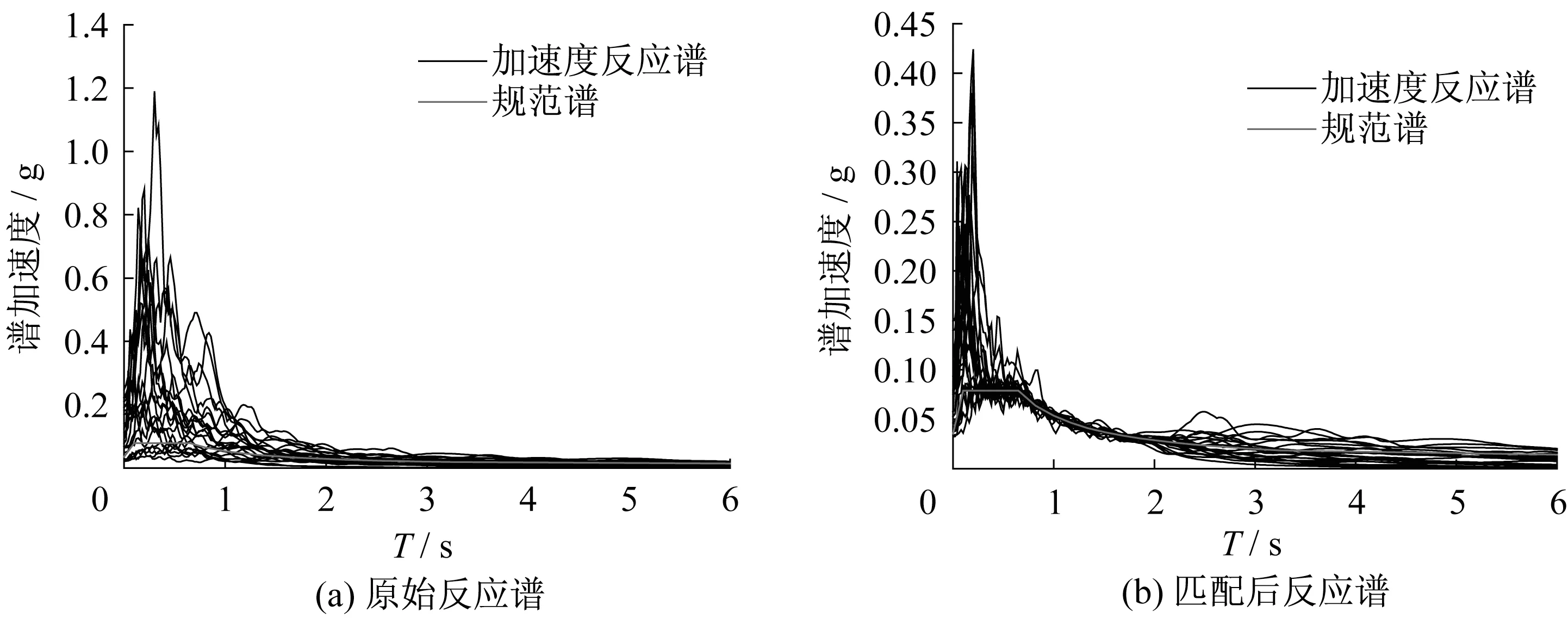
圖3 地震動記錄加速度反應譜Fig.3 Acceleration response spectra of ground motion records

2 結構靜力推覆分析

首先分別對3個結構模型進行模態分析，得到基本自振周期T1和第一振型向量Φ1。5層、8層和11 層結構基本自振周期分別為0.72 s、1.02 s 和1.42 s。取目標位移為1 000 mm，按F1=MΦ1分別對5層、8層和11層結構模型施加側向水平力進行推覆分析，得到基底剪力和頂點位移的關系曲線，即結構的第一振型推覆曲線［17-18］，如圖4所示。

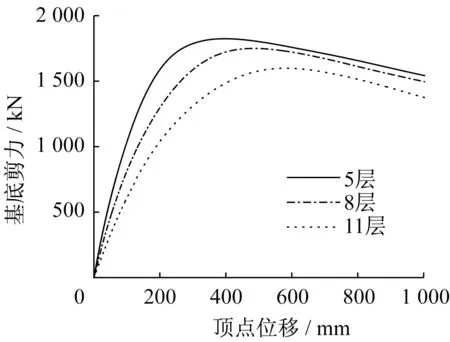
圖4 結構第一振型推覆曲線Fig.4 First-mode pushover curves of structures

圖4 結果表明，當頂點達到設定的目標位移1 000 mm 時，3 個結構的推覆曲線均出現了下降段，且每條曲線具有相似的規律，即加載初期近似于一條通過原點的直線；隨著頂點位移的增大，結構剛度開始減小，結構出現強化段直至基底剪力達到峰值；過峰值點后，曲線出現下降段。據此將第一振型推覆曲線等效為三直線型曲線，如圖5所示。

現以5層結構為例，通過圖6說明等效及相關參數產生的過程:

（1）彈性段:以y=K5-1x+B5-1表示，直線過原點，截距B5-1為0，只需確定斜率參數K5-1，即確定結構的初始剛度。

（2）屈服段:以y=K5-2x+B5-2表示，直線通過原始曲線的峰值點，依據能量等效原理，原始曲線與坐標軸圍成的面積與等效曲線與坐標軸圍成的面積相等。

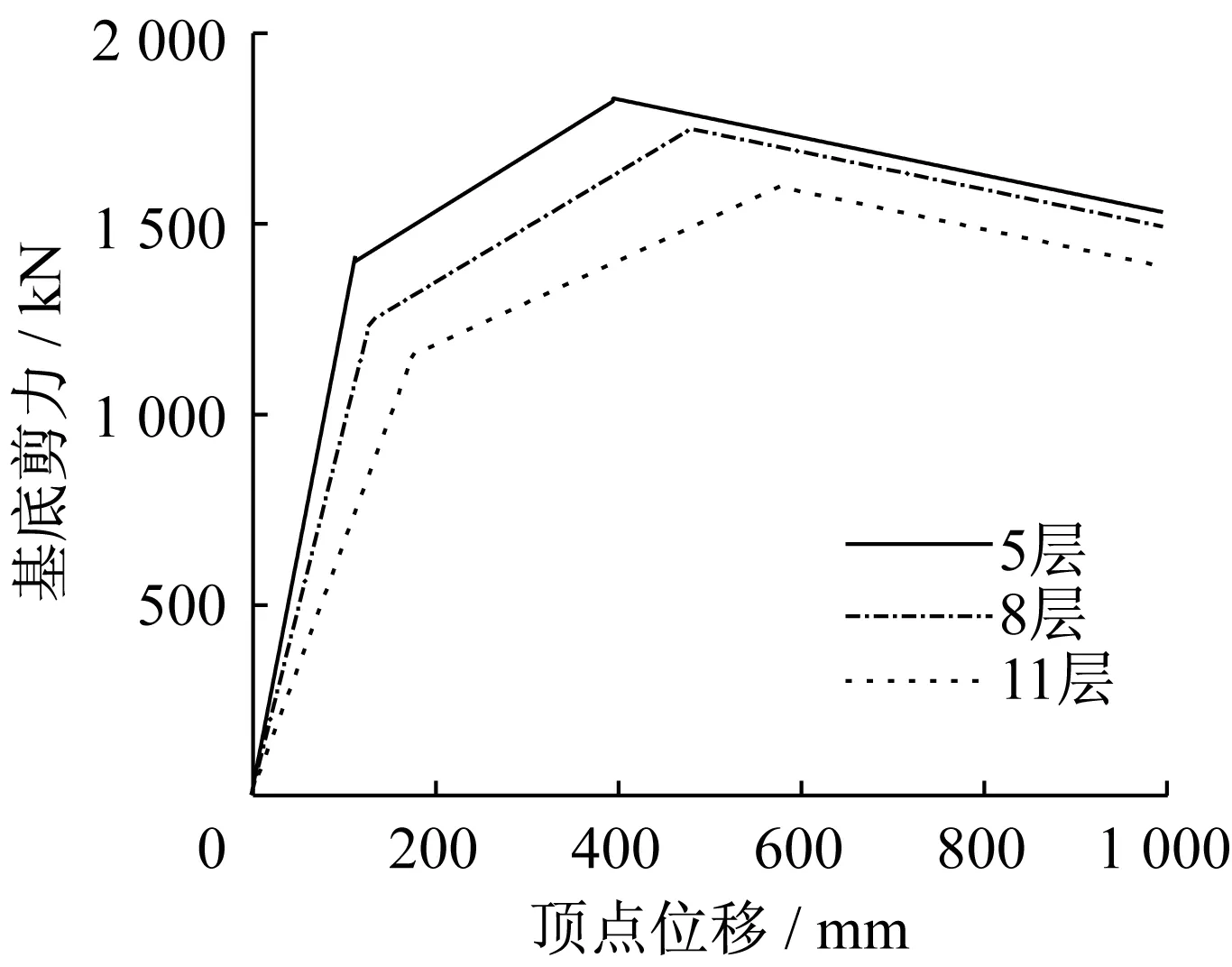
圖5 結構等效三線形推覆曲線Fig.5 Equivalent trilinear pushover curves of structures

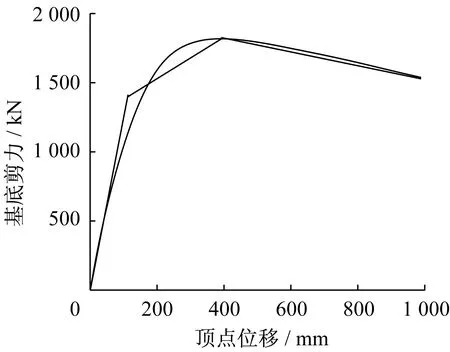
圖6 5層結構第一振型推覆曲線及等效三線形推覆曲線Fig.6 First-mode pushover curve and its equivalent trilinear pushover curve of 5-story structure

（3）下降段:以y=K5-3x+B5-3表示，連接峰值點和位移最大處點的直線即為下降段，其中K5-3為下降段斜率，表示結構的負剛度。

基于此方法，分別求出3個結構模型的等效三線形推覆曲線各直線段方程的參數，如表2 所示。同時表2 中也給出了三個結構模型的屈服后剛度比和下降段剛度比。同樣以5層結構為例，屈服后剛度比定義為屈服段剛度與初始剛度的比值，以α5=K5-2/K5-1表示，下降段剛度比定義為下降段剛度與初始剛度的比值，以β5=K5-3/K5-1表示。

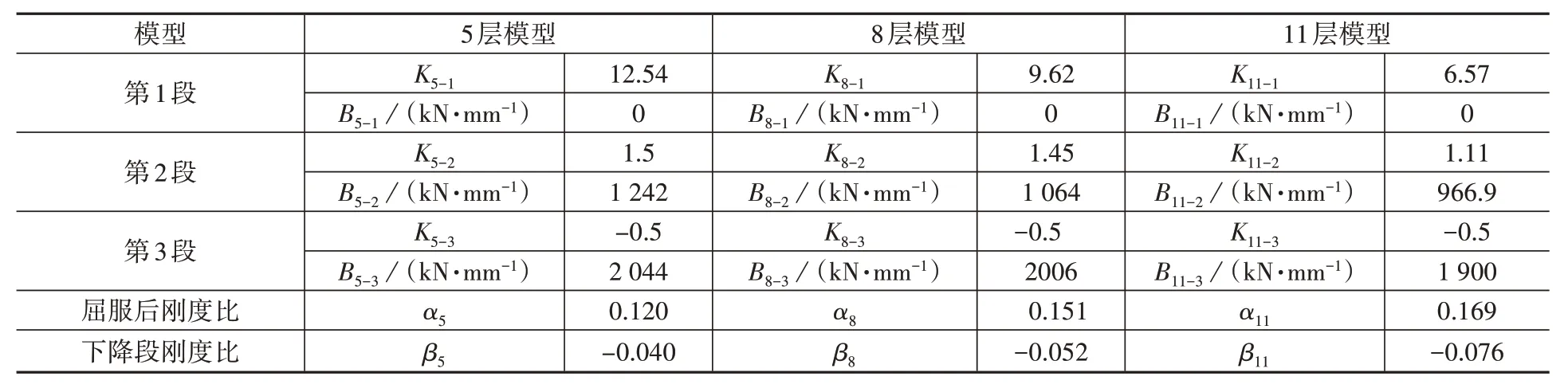
表2 等效三線形推覆曲線各直線段方程參數Table 2 Parameters of straight line segments of equivalent trilinear pushover curves

表2 結果表明，隨著結構層數的增加，即隨著結構高寬比的增大，結構的初始剛度變小，屈服段的剛度也略有減小，下降段的剛度則無明顯變化，而屈服后剛度比和下降段剛度比的絕對值則變大。

3 彈塑性時程分析

3.1 彈塑性時程分析結果統計

將調整到水平1、水平2和水平3的22條地震動記錄分別輸入3 個不同層數的結構模型，進行彈塑性時程分析。本文為研究結構靜止后的殘余位移，在每條地震動記錄原持時的基礎上增加10 s零強度持時，使結構做自由振動直至靜止。分析得到每個結構在每條地震動記錄作用下的最大層間位移角（IDRmax，Maximum Inter-story Drift Ratios）和最大殘余層間位移角（RIDRmax，Maximum Residual Inter-story Drift Ratios），分別計算得到每個結構在相應地震動強度水平下兩個指標的均值、標準差和變異系數，如表3所示。

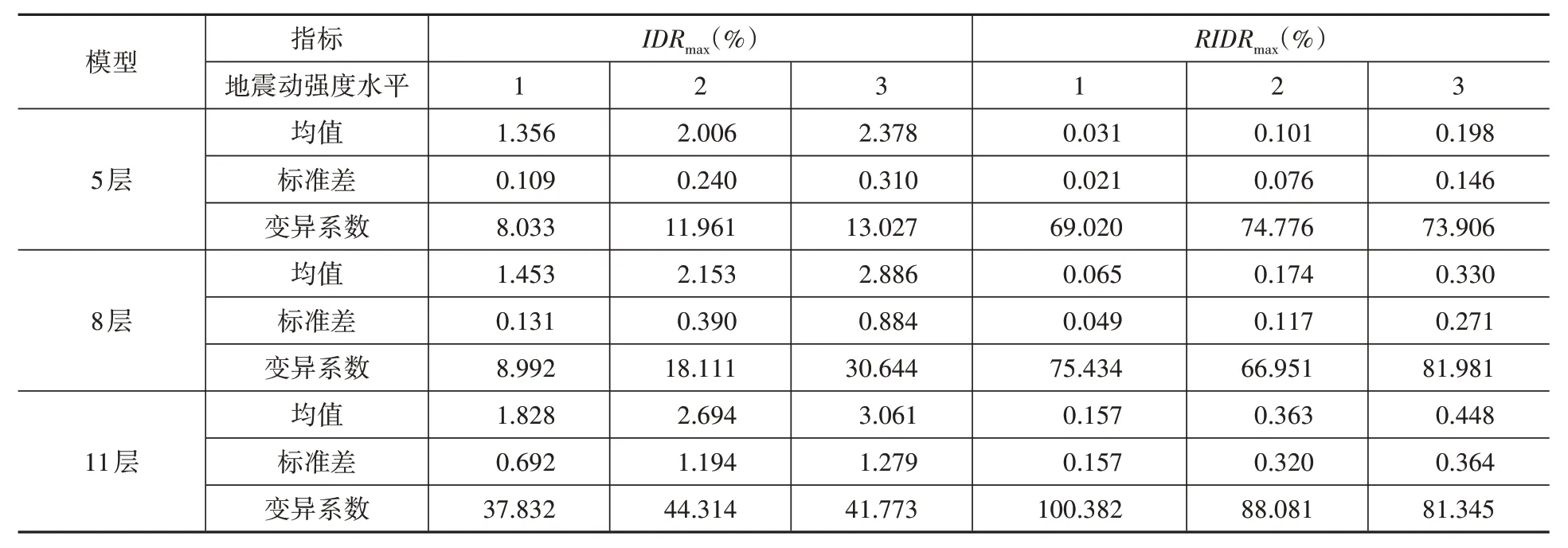
表3 最大層間位移角、最大殘余層間位移角的均值、標準差以及變異系數Table 3 Mean，standard deviation and variation coefficient values of maximum inter-story drift ratio and maximum residual inter-story drift ratio of the structures

表3 結果表明，對同一結構，最大層間位移角和最大殘余層間位移角的均值均隨地震動強度水平的提高而增大；最大層間位移角響應的離散性隨著地震動水平的提高而增大，而最大殘余層間位移角的離散性則無此規律。同一地震動強度水平下，最大層間位移角和最大殘余層間位移角的均值隨著樓層數的增加而增大；最大層間位移角的離散性隨著樓層數的增加而增大，且最大殘余層間位移角的離散性也基本上遵循此規律，但沒有最大層間位移角響應的規律性明顯。

3.2 最大層間位移角和最大殘余層間位移角沿結構高度的分布

5 層、8 層、11 層結構在 3 個不同地震動強度水平下的最大層間位移角和最大殘余層間位移角的均值沿結構高度的分布分別如圖7 和圖8所示。

圖7 最大層間位移角沿樓層高度的分布Fig.7 Distribution of the maximum inter-story drift ratios along structural height

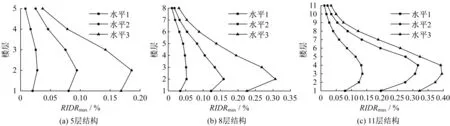
圖8 最大殘余層間位移角沿樓層高度的分布Fig.8 Distribution of the maximum residual inter-story drift ratios along structural height

圖7、圖8結果表明，隨著樓層數的增加，結構的最大層間位移角和殘余層間位移角也呈增大趨勢。

3.3 屈服后剛度比對最大殘余位移角響應RIDRmax的影響

依據靜力推覆分析結果，得到不同結構對應的整體特性屈服后剛度比α和下降段剛度比β。在不同的地震動強度水平下，不同屈服后剛度比所對應結構在22 條地震動記錄輸入下的最大殘余層間位移角平均值如圖9所示。

圖9 結果表明，3 個不同的地震動強度水平下，最大殘余層間位移角的均值均隨著屈服后剛度比的增大而增大，且其離散性也隨著結構屈服后剛度比的增大而增大。對于單自由度體系，結構的屈服后剛度比是影響結構殘余位移響應最關鍵的因素，即殘余位移響應隨著屈服后剛度比的增大而減小［19］。而多自由度體系鋼筋混凝土結構的屈服后剛度比，作為結構的整體特性受結構的高度、質量、構件尺寸等多重因素的影響，這與單自由度的屈服后剛度比對結構殘余位移響應的影響規律不同甚至截然相反。

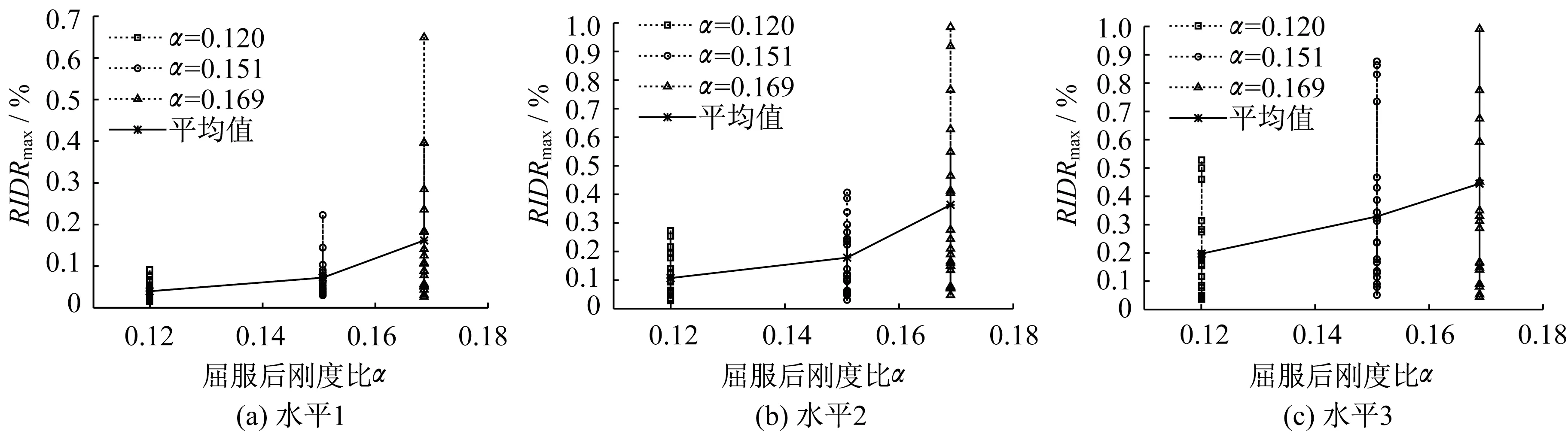
圖9 屈服后剛度比對最大殘余層間位移角的影響Fig.9 Effect of post-yielding stiffness ratios on maximum residual inter-story drift ratios

3.4 下降段剛度比對最大殘余位移角響應RIDRmax的影響

在不同的地震動強度水平下，不同下降段剛度比所對應結構在22 條地震動記錄輸入下的最大殘余層間位移角平均值如圖10所示。

圖10 結果表明，3 個不同的地震動強度水平下，最大殘余層間位移角的平均值均隨著下降段剛度比的絕對值的增大而增大；同時，其離散性也隨著結構下降段剛度比的絕對值的增大而增大。與屈服后剛度比的影響類似，多層鋼筋混凝土結構下降段剛度比對最大殘余層間位移角的影響與單自由度體系下降度剛度比對殘余層間位移響應的影響規律不同。

3.5 結構基本自振周期對最大層間位移角和最大殘余層間位移角響應的影響

結構周期，特別是結構的基本自振周期，是結構本身最重要的整體性特性，因為它包含了結構的整體質量和抗側剛度的信息［20］。結構基本自振周期對最大層間位移角和最大殘余層間位移角在不同地震動強度水平下的影響如圖11所示。

圖11 結果表明，最大層間位移角和最大殘余層間位移角均隨著結構周期和地震動強度水平的增大而增大。結構響應，特別是最大殘余層間位移角響應，受結構基本周期的影響相當明顯。

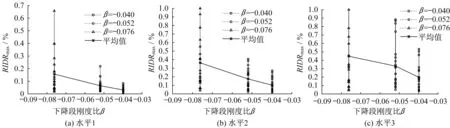
圖10 下降段剛度比對最大殘余層間位移角響應的影響Fig.10 Effect of post-capping stiffness ratios on the maximum residual inter-story drift ratios

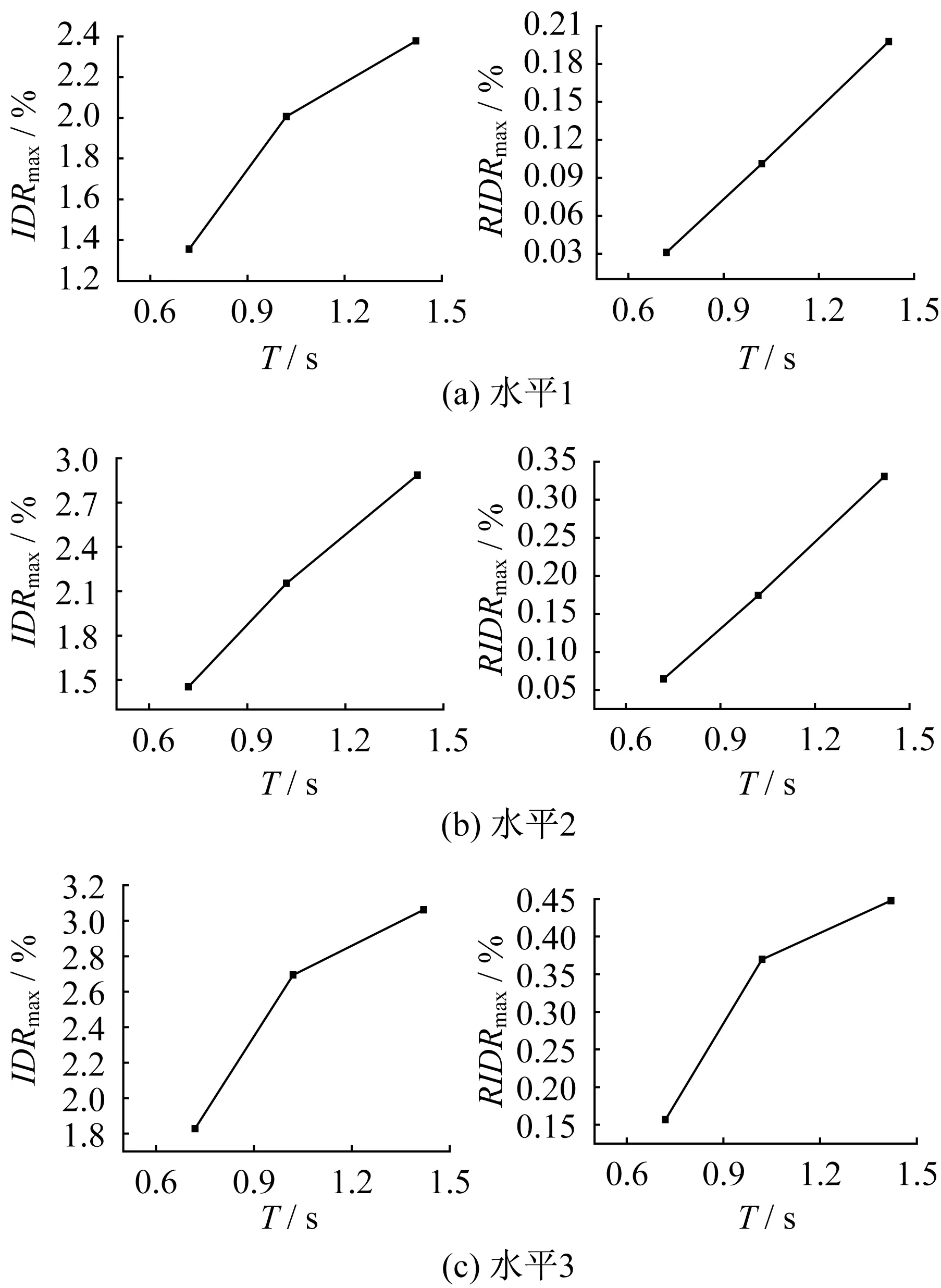
圖11 結構基本自振周期對最大位移響應和最大殘余位移響應的影響Fig.11 Effect of fundamental vibration periods of structures on the maximum inter-story drift ratios and maximum residual inter-story drift ratios

3.6 最大層間位移角響應和最大殘余層間位移角響應的相關性

為了通過層間位移角響應來估算殘余層間位移角響應，利用線性相關系數ρ研究二者之間的相關性。圖12 給出了三種不同結構模型在不同地震動強度水平下最大層間位移角IDRmax和最大殘余層間位移角RIDRmax之間的線性相關系數沿著樓層的分布。

圖12 結果表明，結構底部樓層的IDRmax和RIDRmax的相關性較好，隨著樓層上移，兩者的相關性趨弱。對于最大位移響應和殘余位移響應均比較大的底部樓層，在較大的地震動強度水平下，其相關性一般都較大。這說明結構進入非線性越強，最大位移響應和殘余位移響應的相關性越大。對于不同高度的結構而言，隨著地震動強度水平的增大，兩者的相關性沿著結構高度的分布沒有明顯的規律。

4 結 論

通過對3 個多高層鋼筋混凝土框架結構進行靜力推覆分析和22條地震動記錄在3個不同地震動強度水平下的彈塑性時程分析，研究整體結構特性對鋼筋混凝土框架包括殘余位移指標的響應影響，得到結論如下:

（1）在同一地震動強度水平作用下，多高層鋼筋混凝土框架結構的樓層數越多，最大層間位移角和最大殘余層間位移角響應也越大。最大層間位移角響應的離散性隨著樓層數的增加而增加，且殘余層間位移角的離散性也基本上符合這一變化規律，但其變化沒有最大層間位移角明顯。

（2）最大層間位移角和最大殘余層間位移角均受結構基本自振周期影響明顯，同一地震動強度水平下，兩者均隨結構基本自振周期的增大而增大。相比最大層間位移角，最大殘余層間位移角的增長速度更快。

（3）隨著結構屈服后剛度比的增大和下降段剛度比絕對值的增大，最大殘余層間位移角也增大，其離散性也隨之變大。

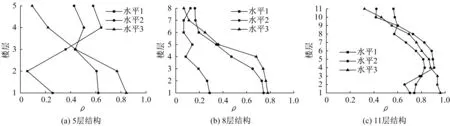
圖12 最大層間位移角和最大殘余層間位移角的相關系數分布Fig.12 Correlation coefficient distribution of maximum inter-story drift and maximum residual inter-story drift

（4）結構下部樓層的最大殘余層間位移角和最大層間位移角的相關性較好，隨著樓層上移，兩者的相關性趨弱。