基于逆可靠度法的鋼管混凝土拱肋穩定性分析

袁騰文

（山西省交通規劃勘察設計院，太原030012）

0 引 言

近二十多年中，鋼管混凝土拱橋在我國得到了大量的應用［1］。拱肋以受壓為主，穩定性驗算是拱肋設計中的關鍵問題。隨著鋼管混凝土拱橋跨徑的不斷增大，拱肋的穩定性問題越來越突出。

一般通過確定性模型計算的拱肋穩定安全系數來確保拱肋不發生失穩破壞［2-5］，但沒有考慮橋梁結構中存在的不確定性因素［6］（如材料特性、偏心距、長細比、外荷載等）。因此，實際的拱肋穩定性安全度是未知的。

可靠度分析為鋼管混凝土拱肋穩定性分析時考慮橋梁結構中的不確定性因素提供了有效的方法。許福友等［6］分析了丫髻沙大橋在某荷載工況下拱肋5 個關鍵截面的穩定性可靠度。滕啟杰等［7］采用JC法分析了一窄鋼管混凝土拱橋拱肋的穩定性可靠度。林道錦等［8］采用可靠度隨機有限元分析了某鋼筋混凝土拱橋面內穩定性可靠度，并進行了靈敏度分析。

目前的橋梁設計規范通過定義目標可靠指標來確保結構安全，因此需要通過校正拱肋穩定安全系數來保證事先給定的目標可靠度指標，從而建立起目標可靠指標和拱肋穩定安全系數間的聯系。逆可靠度分析是給定目標可靠指標，基于已知的極限狀態方程反求未知參數，從而使得未知參數和目標可靠指標相對應。國內外學者對逆可靠度法在工程中的應用進行了一些研究。Cheng等［9］將逆可靠度法運用于評估大跨度懸索橋主纜安全系數。Babu 等［10］將逆可靠度法運用于鋼板樁墻的設計。蘇永華等［11］采用逆可靠度法評估了邊坡的穩定性。方硯兵等［12］采用逆可靠度法計算了隧道支護抗力。雖然逆可靠度法已經用于解決多種工程問題，但將逆可靠度法用于評估鋼管混凝土拱肋穩定安全系數的文獻較少［13］。

本文以鋼管混凝土拱肋為研究對象，基于一次逆可靠度算法對鋼管混凝土拱肋的局部穩定安全系數進行評估，從而建立起具有目標可靠指標和穩定安全系數的拱肋穩定性評估方法。

1 逆可靠度方法

1.1 逆可靠度問題

逆可靠度分析是給定目標可靠指標，基于已知的極限狀態方程反求未知參數。文獻［14］將逆可靠度問題定義為:

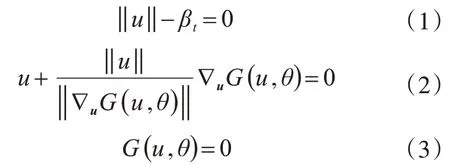
式中:u為標準正態隨機變量；βt為目標可靠指標；?uG(u'θ)為梯度算子；θ為未知參數；G(u'θ)為功能函數。

1.2 一次逆可靠度算法

針對單一參數的逆可靠度問題，文獻［15］提出了一次逆可靠度算法（IFORM），基本思路為:給定βt，在滿足的條件下求解未知參數。

由FORM 基本原理可知，標準正態隨機變量u在驗算點處滿足式（4）:

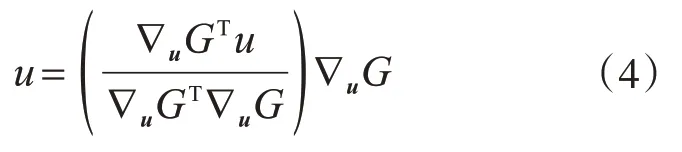
目標可靠指標由式（5）計算:

聯立式（4）和式（5），可得:

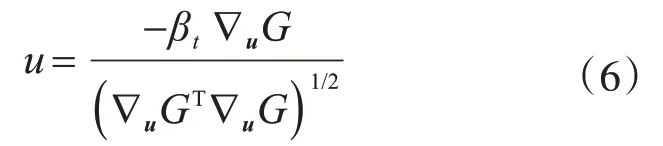
假定未知參數θ的迭代初值為θ0，并將極限狀態方程在θ0處進行泰勒級數展開:

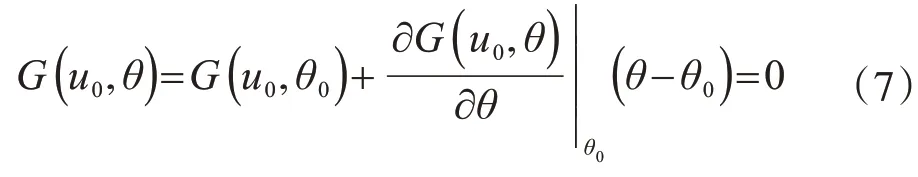
由式（7）可得:

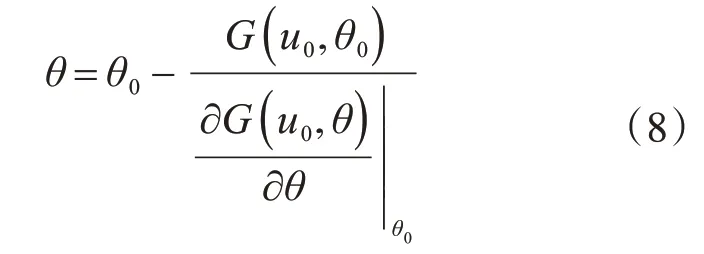
給定隨機變量u和未知參數θ的迭代初值為u0和θ0，計算?uG值代入式（6）得到更新的u1，繼而根據式（8）得到更新的θ1，以迭代更新的u1和θ1作為新的迭代初值，如此反復迭代直至滿足式（9）所示的收斂條件:

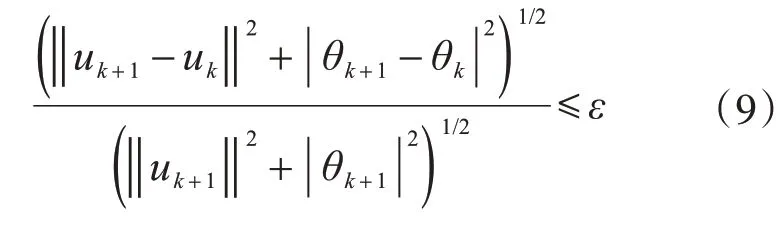
式中，ε為收斂誤差，通常可取0.000 1。

2 基于逆可靠度的拱肋穩定性分析法

2.1 極限狀態方程

基于逆可靠度法的鋼管混凝土拱肋穩定安全系數計算實際上就是給定目標可靠指標反求穩定安全系數，將穩定安全系數定義為

式中:R為拱肋穩定承載力；S為作用效應；θ為穩定安全系數。

根據式（10）建立式（11）所示的極限狀態方程:

2.2 實施步驟

基于一次逆可靠度算法的鋼管混凝土拱肋穩定性分析的計算步驟如下:

步驟1:輸入目標可靠指標βt，收斂誤差ε，假定隨機變量初值和穩定安全系數初值，隨機變量初值一般可取均值，初始化迭代次數j=1。

步驟2:計算極限狀態方程在迭代值處的?uG，并按式（6）更新u。

步驟3:計算G(u0'θ0)和并按式（8）更新穩定安全系數θ。

步驟5:計算式（9）所示的收斂條件，若滿足，則結束計算，輸出結果；否則令j=j+1，返回步驟2繼續計算。

3 實例分析

鋼管混凝土拱肋在受到彎矩、軸力、剪力共同作用時，可以簡化處理成偏心受壓柱，整體承載能力計算公式為［7］

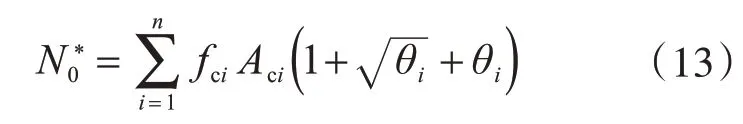
式中:fci為混凝土抗拉強度設計值；Aci為鋼管內混凝土橫截面面積；θi為鋼管混凝土的套箍指標，θi的計算公式為

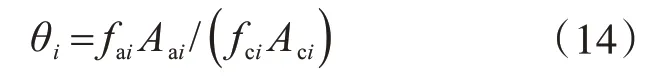
式中:fai為鋼材強度設計值；Aai為鋼管橫截面面積。

依據式（12）-式（14），拱肋穩定承載力R可表示為

式中:X1和μ1為考慮長細比、偏心率和計算模式后的折減系數隨機變量和均值；X2和μ2為混凝土強度隨機變量和均值；X3和μ3為鋼材強度隨機變量和均值。

以文獻［7］中的鋼管混凝土拱橋為例，文獻［7］中給出了拱肋穩定性分析時在某荷載工況下拱肋5 個關鍵截面的極限狀態方程。按本文的求解思路，將穩定安全系數引入到已有的5 個極限狀態方程中，拱腳截面、L/8 截面、L/4 截面、3L/8 截面和跨中截面的極限狀態方程分別為

式中:X4為作用效應隨機變量；θ為穩定安全系數。

四個隨機變量的分布類型及統計參數見表 1［6-7］。

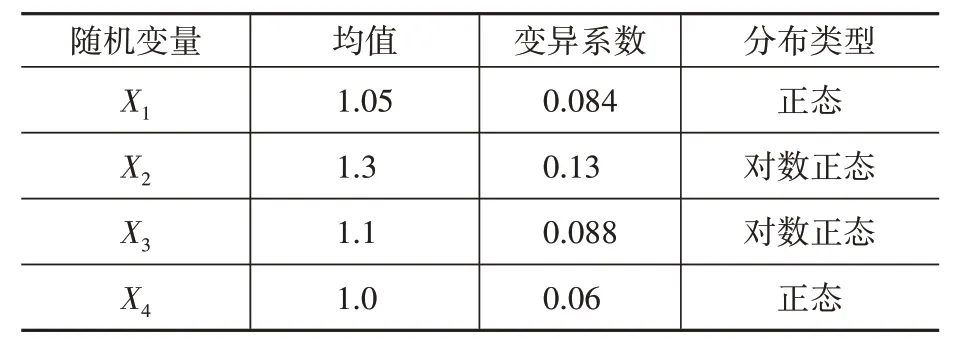
表1 分布類型及統計參數Table 1 Distribution type and statistical parameters

3.1 穩定安全系數求解

參照《公路工程結構可靠度設計統一標準》（GB/T 50283—1999）［16］，按結構安全等級和構件破壞類型對目標可靠指標進行取值，目標可靠指標分別取3.7、4.2、4.7 和5.2，收斂誤差ε=10-4，拱肋5 個關鍵截面在不同目標可靠指標下穩定安全系數的計算結果如圖1所示。

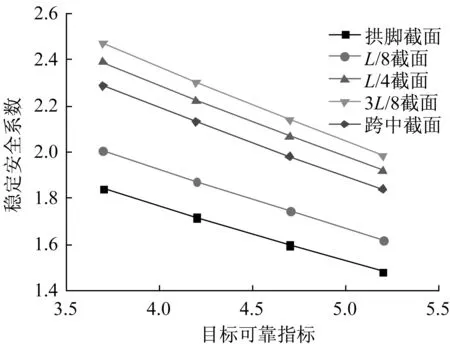
圖1 可靠度水平對穩定安全系數的影響Fig.1 Impact of reliability level on stability safety factor

由圖1 可知:隨著目標可靠指標逐漸增加，各截面的穩定安全系數均呈遞減趨勢，說明不同的目標可靠指標，拱肋穩定性所需的安全儲備是不同的，因此穩定安全系數各異；目標可靠指標取值對穩定安全系數有較大影響，因此在實際計算時應合理的確定目標可靠指標；3L/8 截面的穩定安全系數最大，其次是L/4 截面，拱腳截面的穩定安全系數最小。

3.2 驗證

將逆可靠度分析求得的穩定安全系數作為已知參數，采用FORM 方法求得可靠指標的計算結果見表2。

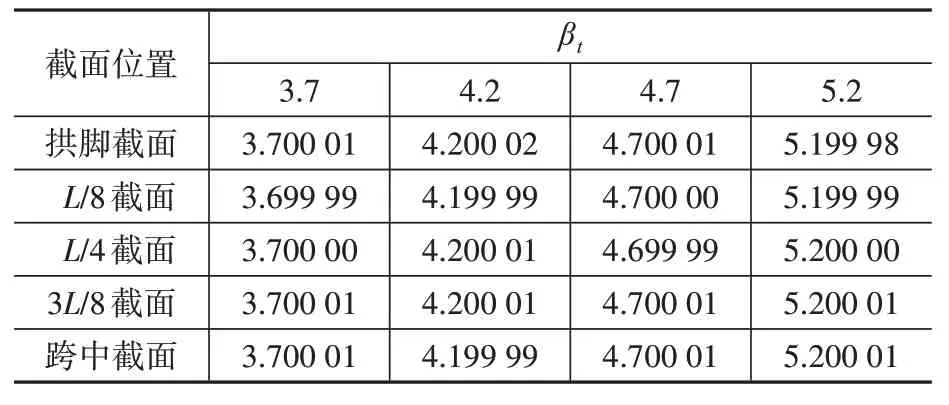
表2 FORM結果Table 2 Results of FORM

由表2 可知，采用FORM 求得的可靠指標與逆可靠度分析時給定目標可靠指標相差很小，說明一次逆可靠度算法可以滿足工程精度要求。

3.3 參數分析

3.3.1 隨機變量均值的影響

為了研究隨機變量均值對穩定安全系數的影響，以跨中截面為例，取目標可靠指標βt=3.7，收斂誤差ε=10-4，分別令各隨機變量均值變化-10%～10%，隨機變量變異系數不變，求得的穩定安全系數如圖2所示。

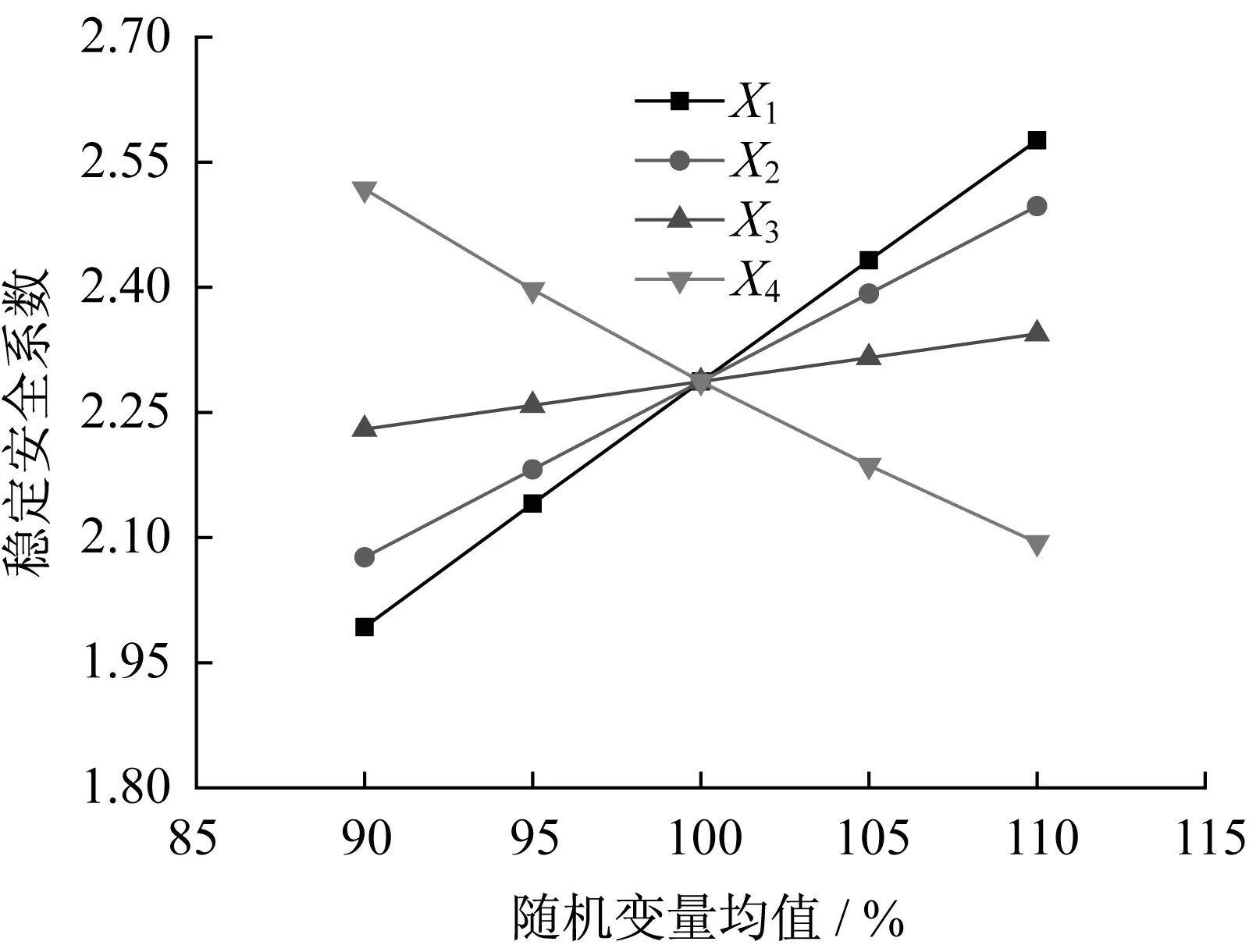
圖2 隨機變量均值與穩定安全系數的關系Fig.2 Relationship between mean value of parameters and stability safety factors

由圖2可知:隨著折減系數X1、混凝土強度X2和鋼材強度X3均值逐漸增加，穩定安全系數均呈遞增趨勢；隨著作用效應X4均值逐漸增加，穩定安全系數呈遞減趨勢；折減系數X1對穩定安全系數影響顯著，混凝土強度X2和作用效應X4對穩定安全系數的絕對影響程度相當，鋼材強度X3對穩定安全系數影響相對較小。

3.3.2 隨機變量變異系數的影響

為了研究隨機變量變異系數對穩定安全系數的影響，以跨中截面為例，取目標可靠指標βt=3.7，收斂誤差ε=10-4，分別令各隨機變量變異系數變化-10%～10%，隨機變量均值不變，求得的穩定安全系數如圖3所示。

圖3 隨機變量變異系數與穩定安全系數的關系Fig.3 Relationship between variability of parameters and stability safety factors

由圖3 可知:隨著隨機變量變異系數逐漸增加，穩定安全系數對著隨機變量變異系數的逐漸增大而呈遞減趨勢；穩定安全系數對折減系數X1最敏感，其次是混凝土強度X2，穩定安全系數對鋼材強度X3最不敏感。

4 結 論

提出了一種基于逆可靠度分析的鋼管混凝土拱肋穩定安全系數的評估方法，通過一次逆可靠度算法將目標可靠指標和穩定安全系數聯系起來，求得的穩定安全系數滿足預先給定的目標可靠指標，同時考慮了結構中存在的不確定性因素。通過實例分析，得出以下結論:

（1）隨著目標可靠指標的逐漸增加，拱肋穩定安全系數呈遞減趨勢，不同的目標可靠指標，拱肋穩定性所需的安全儲備不同；

（2）折減系數對拱肋穩定安全系數的影響顯著，鋼材強度對拱肋穩定安全系數的影響相對較小。