斜拉橋錨拉板式索梁錨固區尺寸參數靈敏度分析

陳彥江 黎兵兵 許維炳，* 辛光濤，2 崔 濤

（1.北京工業大學，北京100124；2中國公路工程咨詢集團有限公司，北京100089）

0 引 言

斜拉橋拉索和主梁連接的部分應力集中、構造復雜，是橋梁結構設計要著重關注的區域［1］。目前斜拉橋結構設計過程中主梁和拉索錨固連接的主要構造形式有錨拉板式、耳板式、錨箱式、錨管式等［2］。近年來，無論國內還是國外學者對錨固結構的構造設計和受力性能進行了不同程度的研究。劉慶寬等通過實際的工程案例結合足尺模型的有限元分析和試驗數據，對錨箱式索梁錨固結構的應力分布、大小和極限承載力進行了專項研究［3］，并結合杭州灣跨海大橋和南京二橋工程實例的施工過程，對耳板式索梁錨固結構進行了足尺模型試驗，探究了變化的拉索索力荷載作用下錨固區結構設計的合理性和荷載傳遞的可靠性［4］；任偉平等依托具體的實例工程，先后對錨拉板式索梁錨固結構進行了足尺模型的靜力和動力學試驗，探究索梁錨固結構的應力集中分布、塑性區域的大小以及關鍵部位疲勞力學的性能等［5］；王歲利等結合汕頭巖石大橋的工程案例研究了錨管式索梁錨固結構錨管角度精度的控制方法［6］。王子健等僅探討了索梁錨固結構各類結構尺寸參數與結構之間的曲線關系，并未給出各尺寸參數對結構影響程度的度量標準［7］。

與其他索梁錨固結構形式相比，雖然錨拉板式索梁錨固結構具有相對簡單的構造形式、易于加工、后期的維護保養等操作相對容易等優勢，但是其結構的部分區域易出現局部應力集中，設計荷載作用下出現塑性區域的現象可能性較高，因此研究索梁錨固結構的尺寸參數對結構的影響是十分具有實用價值的。筆者結合某具體的斜拉橋工程實例，通過進行索梁錨固結構足尺模型力學試驗得到的試驗數據驗證有限元數值分析的合理性，研究在不同的錨拉板式索梁錨固結構尺寸參數下結構的變化規律，并通過Sobol全局敏感性分析方法［8］探究各類尺寸參數對結構的敏感性，為以后相關研究提供參考。

1 工程概況

本文依托的工程案例為一座獨塔斜拉單索面鋼筋-混凝土結合梁橋，主跨（254 m）為懸空拼接的鋼箱梁，邊跨（48.2 m+87.8 m）為利用滿堂支架現澆的預應力混凝土連續箱梁。整座橋梁總共設置38 對拉索。整體橋型的布置以及錨拉板構造形式分別如圖1和圖2所示。

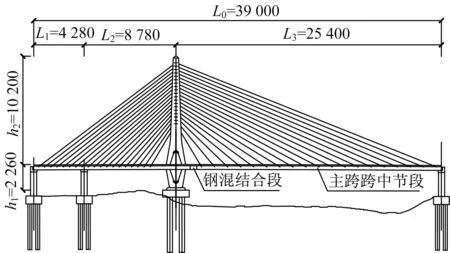
圖1 整橋布置圖（單位:cm）Fig.1 The whole bridge layout（Unit:cm）

如圖2 所示，錨拉板具有相對簡單的構造形式:上部連接拉索的錨管與錨拉板的開槽處直接焊接，錨拉板下部直接與主梁焊接，中部為過渡區域提供給不同角度和位置的索梁錨固結構調整空間。通過在錨拉板兩側焊接加勁肋抵消錨拉板上部開槽對其自身強度的削弱并加強其自身的橫向剛度以及整體性。其傳力路徑也相當明確，拉索荷載通過設置在錨管底部的錨墊板傳遞給錨管，然后拉索荷載通過錨管兩側焊縫傳遞給錨拉板，最終經過錨拉板將拉索荷載傳遞到主梁。各構件初始參數如表1所示。

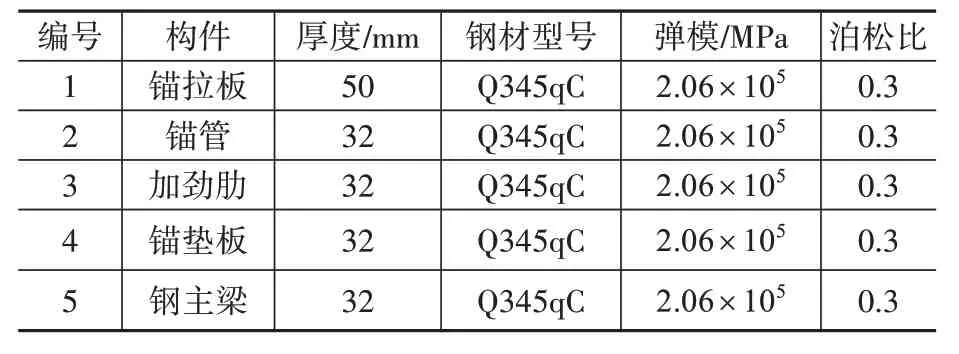
表1 構件參數表Table 1 Parameters of components

2 結構靜力分析

采用結構有限元數值分析軟件ABAQUS數值模擬試驗節段足尺模型。足尺模型有限元數值分析采用空間S4 板殼單元進行模擬，此種類型單元十分適合用于分析平面的彎曲問題，能夠十分精確地求解構造的應力集中問題。足尺模型有限元分析邊界條件設置為約束三向位移的兩端固結約束，主梁與錨拉板的連接設定為綁定接觸，以面荷載的形式將斜拉橋的拉索荷載施加在錨墊板上。足尺模型的有限元模型如圖3所示。足尺模型材料的應力應變曲線采用雙線性等向強化理論。

圖3 有限元模型Fig.3 Finite element model

在試驗設計荷載作用下，有限元模型的應力云圖如圖4所示。

圖4 錨拉板結構應力云圖Fig.4 Stress contour of tensile anchor plate

如圖4 所示，在拉索試驗設計荷載的作用下，斜拉橋錨拉板式索梁錨固結構的位置集中分布在錨拉板和錨管焊接的過渡圓弧處或錨拉板和錨管連接的焊縫處。錨拉板的上部和中部集中了大部分較高的應力水平，說明該部分是斜拉橋錨拉板式索梁錨固結構設計時的強度控制區域。需要說明的是作者在有限元分析過程中，考慮到局部構造模擬的難度比較大，對足尺模型的構造設計進行了局部的簡化（如局部加強焊接方式等），造成構件局部出現應力集中，上述現象表明了局部應力集中區域是足尺模型的薄弱部位，但并不會影響模型整體的傳力路徑。

通過進行節段模型的靜力試驗，驗證試驗模型有限元分析的合理性，構件如圖2 所示，加載和測點布置如圖5 所示。正常使用極限狀態下本橋跨中位置的斜拉索索力約為5×103kN。試驗加載的過程通過分級的形式進行加載，第一部采用設計荷載的50%進行預加載然后卸載，分別進行三次，以達到消除試驗模型非彈性變形對試驗結果的影響；第二部以設計荷載的10%作為一個增量級，逐級累加一直到達設計荷載后再進行分級卸載，每級加載過程的持續時間為10 min；第三部待每級加載過程趨于穩定后對構件的應變量進行測量，過程一直持續到拉索設計荷載5×103kN為止。

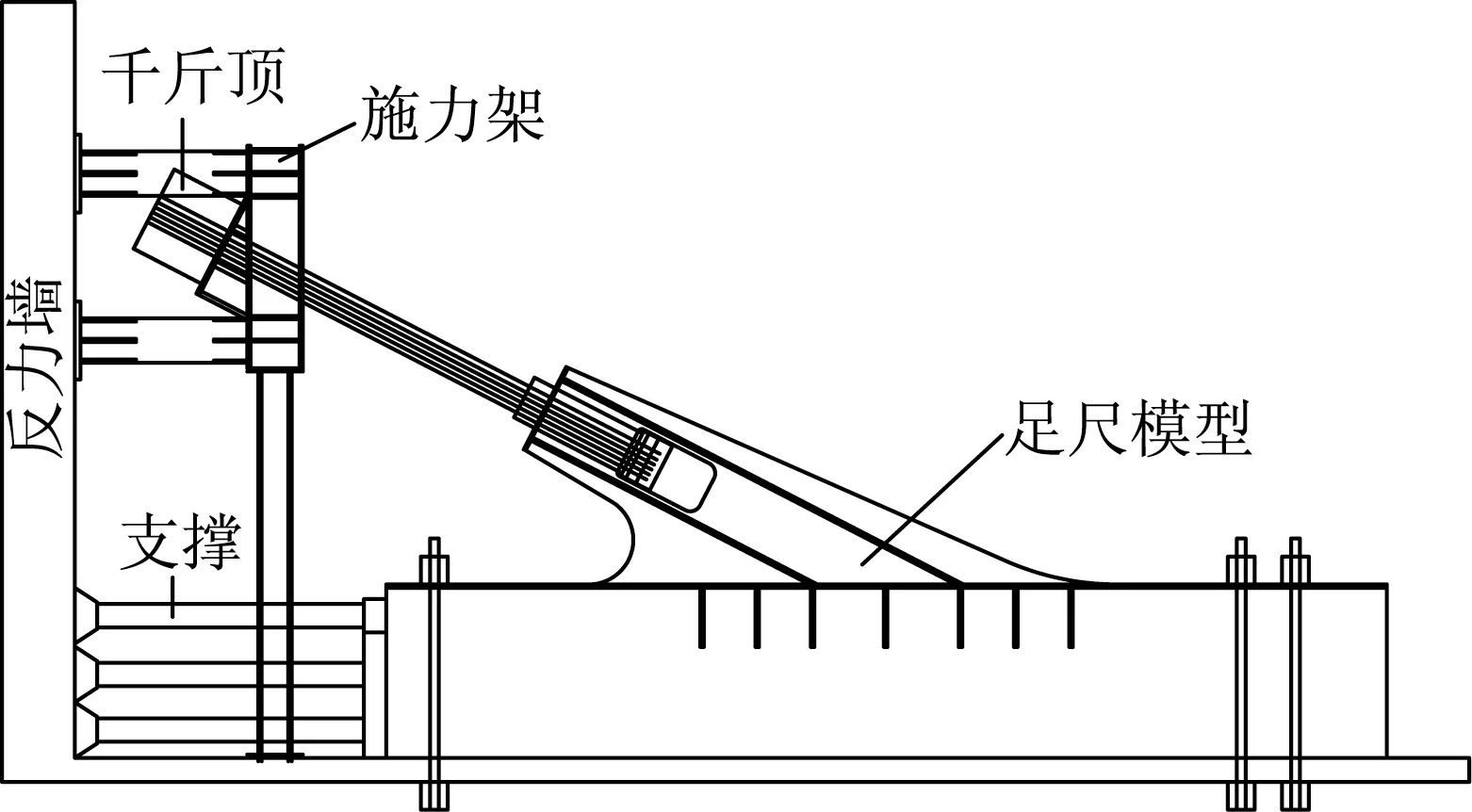
圖5 試驗布置和試驗過程Fig.5 Layout of the load test and process of tests

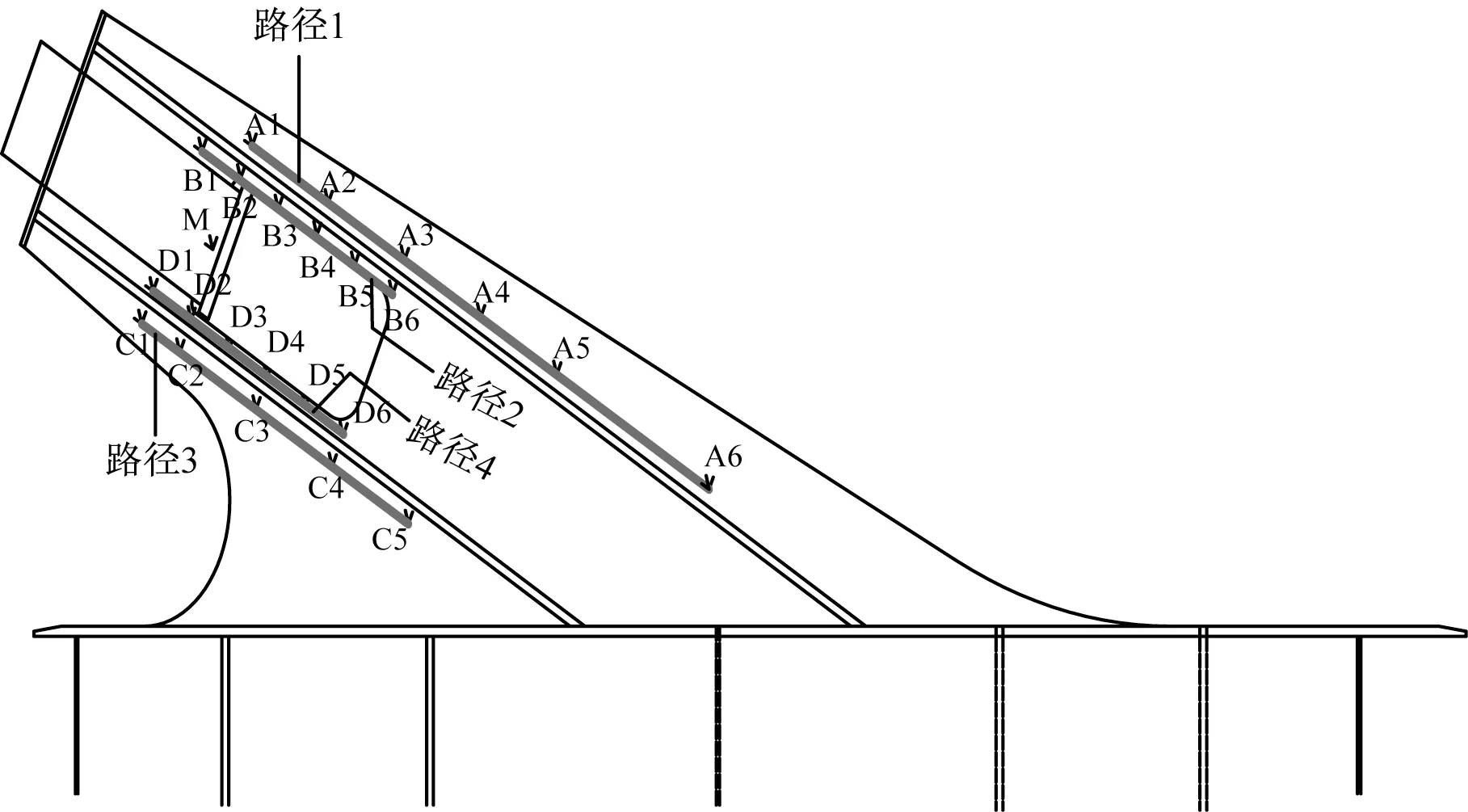
圖6 應變測點布置Fig.6 Layout of measuring points

通過將試驗數據與有限元分析結果進行對比，結果如圖7所示。

由圖7 可知，測點路徑上有限元數值分析結果與試驗實測應力基本一致，實測結果總體比有限元分析結果偏小，但偏差總體較小，論證了有限元分析的合理性，為后續研究提供了理論依據。

3 結構參數分析

基于以上分析結果對錨拉板式索梁錨固結構進行尺寸參數分析研究。結合錨拉板式索梁錨固結構的構造特點，分別選取以下結構參數進行分析研究，材料參數保持一致，具體如圖8和表2所示。

圖7 數據對比Fig.7 Data comparison

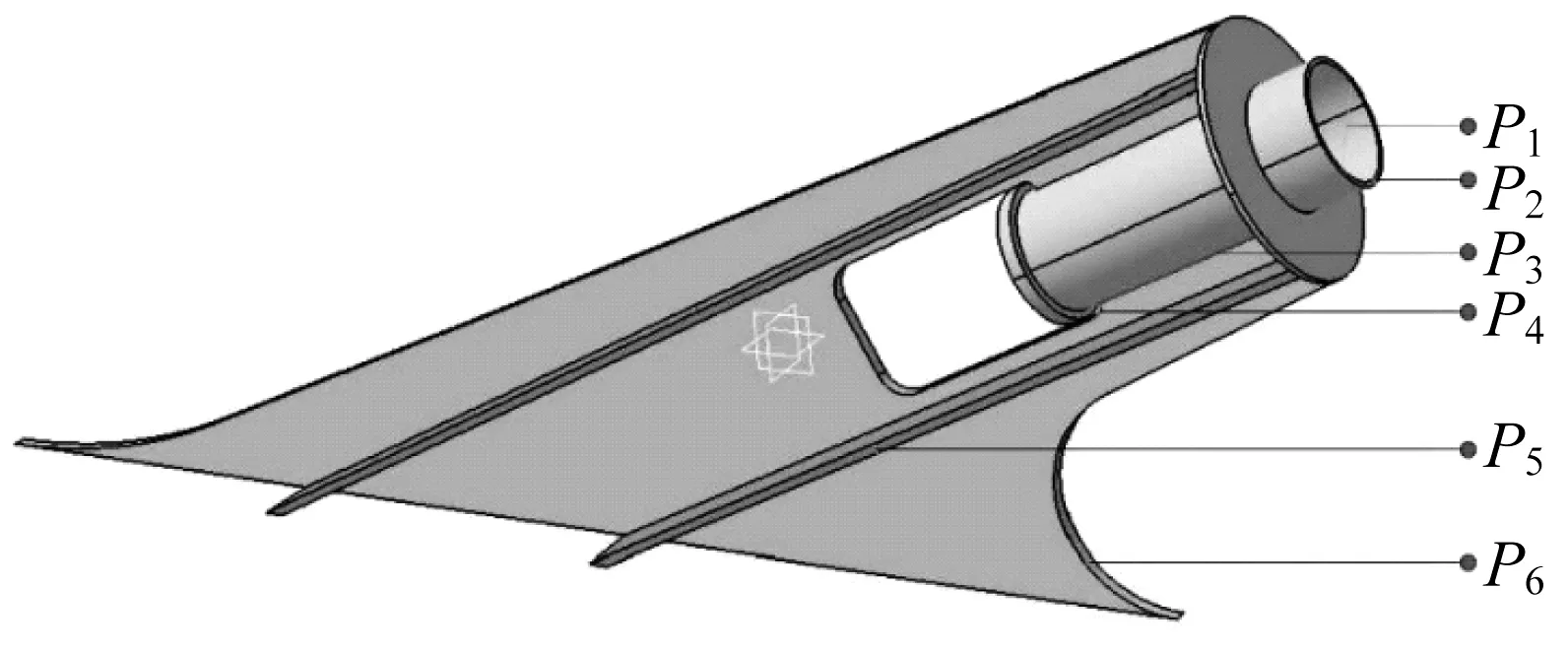
圖8 結構參數位置示意圖Fig.8 Schematic diagram of structural parameters

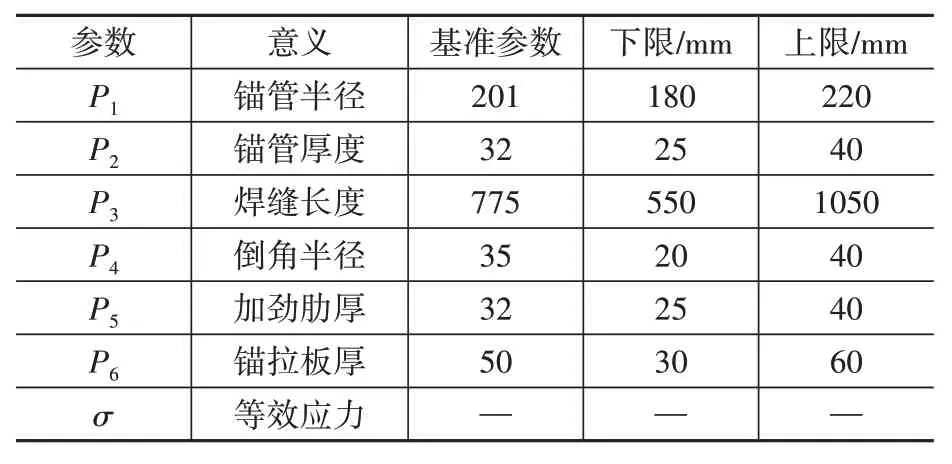
表2 參數意義及取值范圍Table 2 Parameters definition and value range

以錨拉板與錨管的焊縫連接處的作為結構的控制點應力σ。通過編寫Python 程序讓有限元軟件ABAQUS 進行讀取，將上述結構參數設置取值范圍以及運行的步數，可得到控制應力σ 與各結構尺寸參數的應力曲線關系，結果如圖9所示。

通過圖9的結果可以得出結論:控制點應力σ與錨管的半徑呈正向關系，而與錨管的厚度、焊縫的長度、倒角的半徑、加勁肋的厚度以及錨拉板的厚度等因素呈負向關系。為了進一步探究各結構參數對控制點應力σ 的影響靈敏度，接下來通過Sobol 全局靈敏度分析方法探究各結構尺寸參數對控制點應力σ的靈敏度。

4 結構參數靈敏度分析

4.1 Sobol全局靈敏度分析方法

Sobol靈敏度分析算法是一種基于方差的全局靈敏度分析方法［9］，具體計算流程可以如下描述。

假設模型可以表達成Q=f(T)，其中，Q為模型的輸出量，T={ti}(i=1'2'…'m)，其中ti～U(0'1)為參數的輸入量，且f2(T)可積，則模型能被分解成:

式（1）右端的子項共有2m個，且分解方法多種。通過Sobol 分析算法可以得到該模型的總方差為

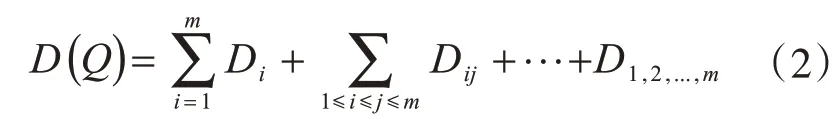
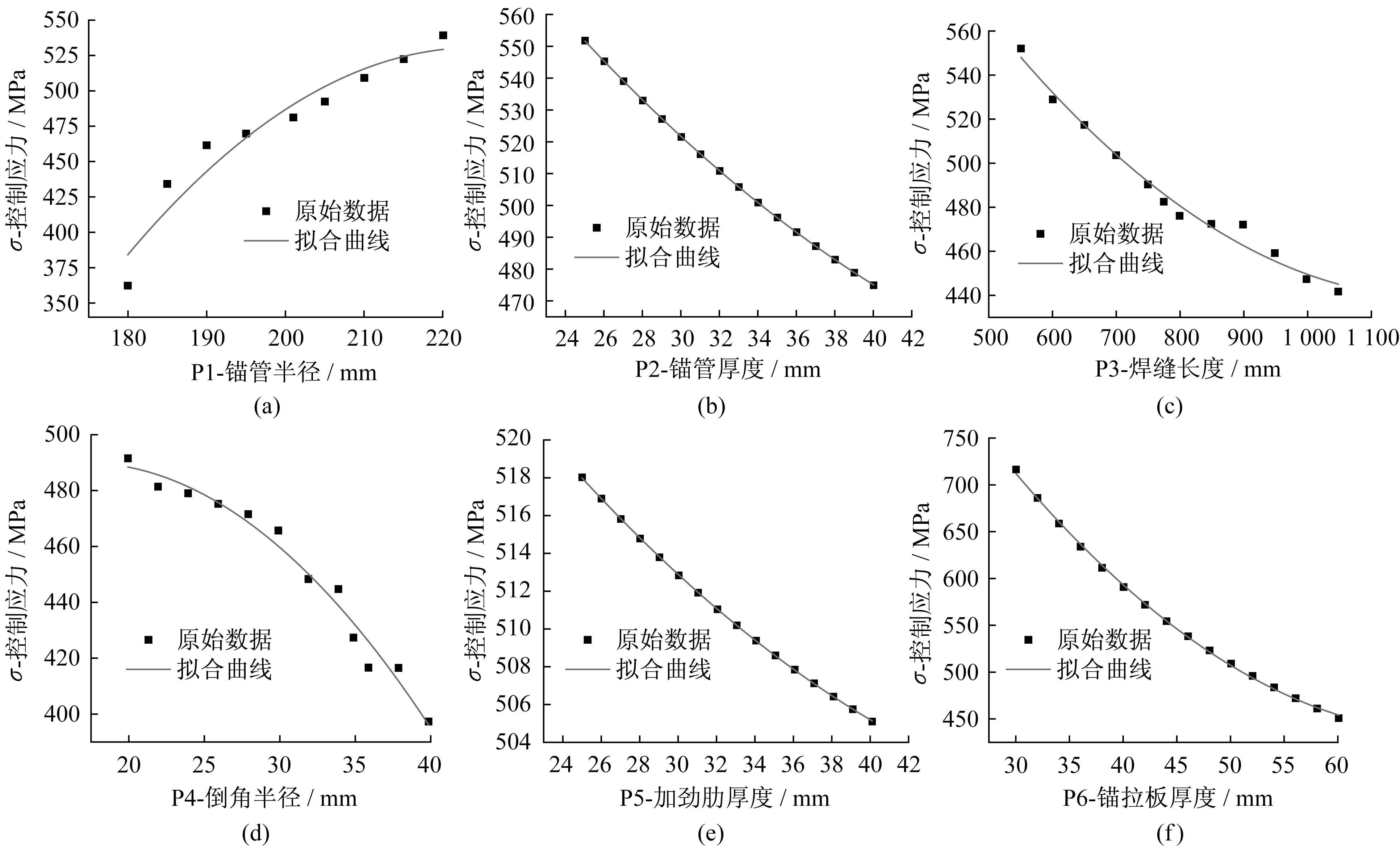
圖9 參數與控制應力關系曲線Fig.9 Relation curves between parameters and control stress

式（2）中，T被調整為一個m 維的超立方體Ωm，D(Q) 為 總方差；Di為參數Ti的方差，也即Dij為參數Ti和Ti相互作用的方差。基于以上分析過程，得到參數Ti的一階敏感度Si和總敏感度SAi可以表示為

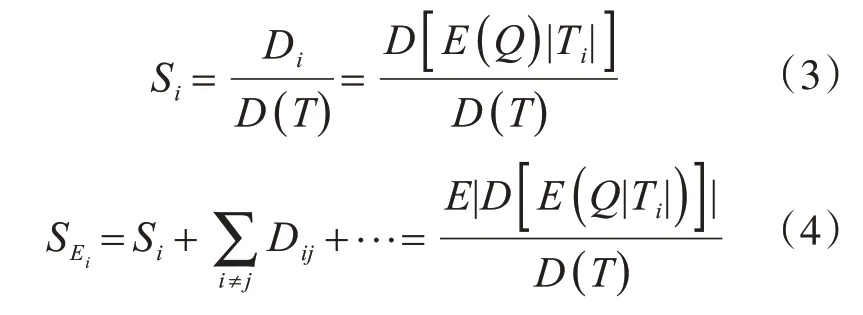
通過創立兩個相互獨立的(k'n)維度矩陣M和N，其中k為采樣數，n為模型變量數，來得到參數Ti的一階敏感度系數Si和總敏感度SEi。而矩陣M和N中的每行相當于模型一個輸入參數T。基于蒙特卡洛方法的D(Q)、Si、SEi的近似解為

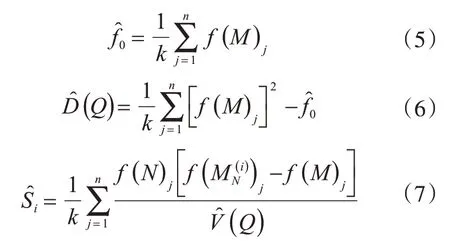
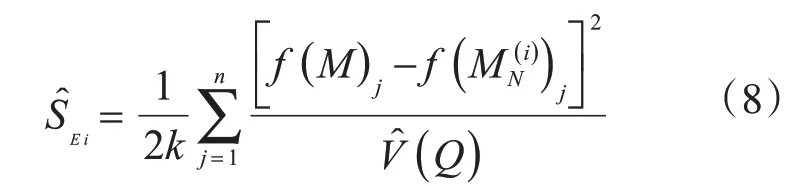
4.2 參數靈敏度分析過程

通過建立控制點應力σ與錨拉板結構尺寸參數之間的數學模型σ=f(P)，其中，P={pi}(i=1'2'...'6)，以便利用Sobol全局靈敏度分析方法來衡量各結構參數相對控制點應力σ的靈敏度。

通過利用各結構尺寸參數與控制點應力σ的對應數據進行曲線擬合，并根據圖6 中各參數與控制點應力σ的關系曲線特征確定各參數的冪指數，具體遵循的規則如下:若結構尺寸參數的關系曲線特征近似呈現直線，則結構尺寸參數只取一次項，否則取其一次項和二次項。通過以上規律，可以得到控制點應力與各結構尺寸參數之間的數學模型為

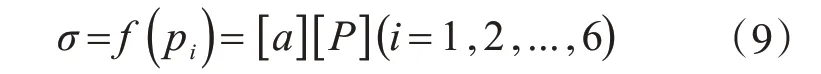
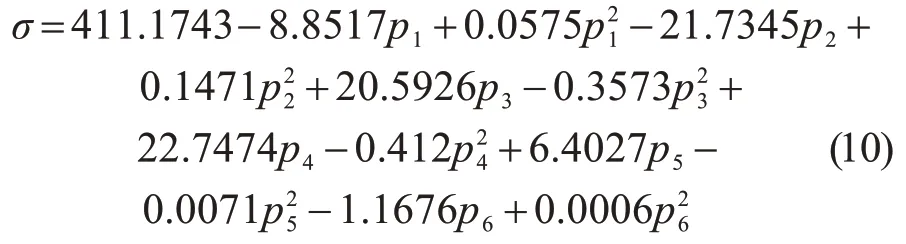
通過以上建立的各結構尺寸參數與控制點應力σ的數學模型和各結構尺寸參數的取值范圍輸入事先已經編寫好的Sobol 全局靈敏度分析方法的程序中，啟動計算程序可以得到各結構尺寸參數，相對于控制點應力σ的全局靈敏度具體數值大小如圖10所示。

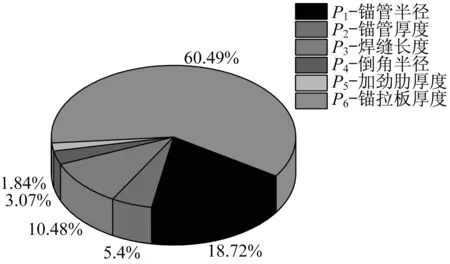
圖10控制點應力靈敏度Fig.10 Stress sensitivity of control points

從圖10 可以得到結論，錨拉板厚度、錨管半徑與焊縫長度對控制點的應力σ影響相對較大，特別顯著的是錨拉板厚度對控制點應力的靈敏度，因此構件結構設計時可以考慮通過這三個方向去設置結構的尺寸參數避免板件屈服的發生。

5 結構設計優化

基于以上結論，本文在初始靜力分析的基礎上，對結果進行了結構尺寸的參數優化，優化的方法是基于改進的EGO 算法，EGO 算法是一種適用于黑箱函數求極值的全局最優化算法，在對目標函數進行少量估值的情況下獲得最優解［10］。

假設有一個系統，其輸出y可以由y=F(x)精確算出，但是F是一個黑箱函數，在數值優化過程中需要選取一個計算相對容易的近似模型y≈G(x)（代理模型 metamode）來替代原有的模型，可以理解為將目標函數minx y=F(x)改變為minx y≈G(x)。本文進行結構尺寸參數優化采用的代理模型為4.2 構建的數學模型式（9），代入事先編好的 EGO 算法程序里。其中，p2，p4，p5保持基 準 參 量 ，p1∈[180'220]，p3∈[550'1 050]，p6∈[30'60]。經多次的迭代計算，控制點應力σ在點p1=197，p3=954，p5=56 處達到最低峰值。從表3 可以得到結論:對比優化前的結構內力水平，優化后的構件控制應力σ下降了20.1%，焊縫處局部平均應力下降了16.5%，焊縫處應力集中系數下降了17.6%，說明經過構件結構尺寸參數優化后結構的受力性能得到了顯著改善，這對今后相關結構尺寸參數優化研究提供參考非常具有意義。

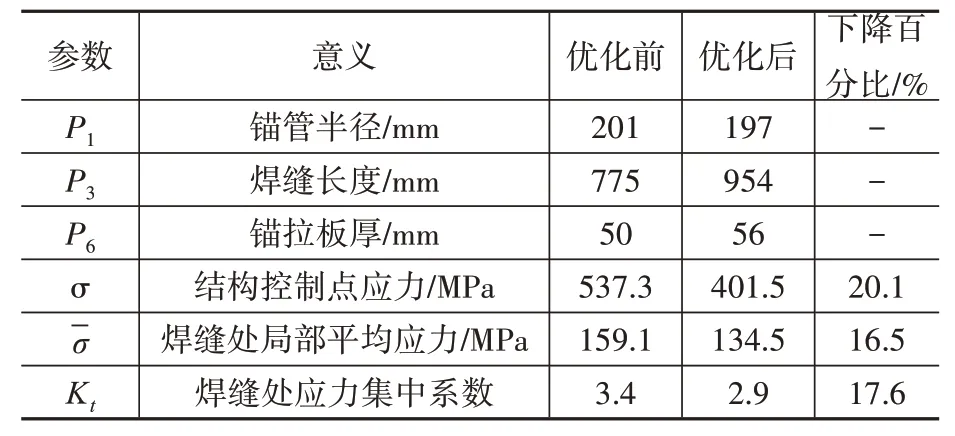
表3 優化結果Table 3 Result of optimization

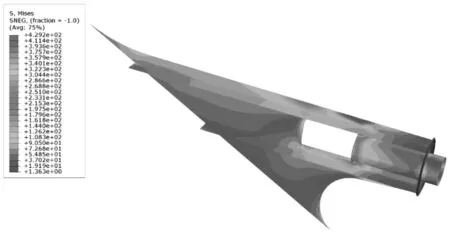
圖11優化參數后結構內力云圖Fig.11 Structural stress contour plot after parameter optimization

6 結 論

本文基于現有的工程實例，采用有限元軟件ABAQUS對錨拉板式索梁錨固結構的尺寸參數對控制點應力σ的靈敏度進行了分析研究，得到結論如下:

（1）通過將有限元分析的數值結果與足尺模型試驗得到數據進行對比，驗證了有限元分析的合理性。

（2）通過編寫及修改ABAQUS 有限元分析軟件內置通用的Python 命令流文件，提取研究對象的結構參數實現參數化建模，大大提高了有限元分析的計算效率。

（3）通過進行有限元靜力分析，在拉索索力設計荷載的作用下錨拉板索梁錨固結構的位置一般集中分布在錨拉板和錨管焊接的過渡圓弧處或錨拉板和錨管的連接焊縫處，該區域為應力集中較為嚴重的區域。

（4）通過研究錨拉板式索梁錨固結構的尺寸參數與結構的關系得到，結構與錨管半徑呈正向關系，與倒角半徑、焊縫長度、錨管厚度、錨拉板厚度、加勁肋厚度呈負向關系。

（5）通過Sobol全局靈敏度分析算法分析錨拉板索梁錨固區結構的尺寸參數相對控制點應力σ的靈敏度可知，索梁錨固區的錨管半徑，錨拉板厚與焊縫長度對結構的控制點應力σ影響較大，尤其索梁錨固區的錨拉板厚對控制點應力σ的靈敏度十分顯著。構造結構設計時需要重點考慮對這三個結構參數進行調整來優化設計減少屈服問題。

（6）基于改進的EGO 優化算法，計算出了使結構控制點應力σ最小的結構參數組合。與優化前的結構內力水平相比，優化后結構的控制應力下降了20.1%，焊縫處局部平均應力下降了16.5%，焊縫處應力集中系數下降了17.6%，表明優化后的結構受力性能改善明顯，為今后相關構造結構設計優化提供借鑒。