非對稱圍壁加強對耐壓圓柱殼孔口應力影響分析

張帆晨，和衛平，馬建軍

(武漢第二船舶設計研究所，湖北 武漢 430061)

0 引 言

水下航行器必須有堅固的耐壓船體來承受巨大水壓力。但由于實際需求，往往要在水下航行器的耐壓結構上開各種各樣的孔，這些孔的存在破壞了耐壓圓柱殼的結構連續性，改變了開孔區域的應力分布，產生開孔處應力集中現象，嚴重降低耐壓圓柱殼的極限承載能力。工程上會采取各種補強措施來彌補由于開孔導致的被削弱殼體強度，避免在開孔周圍造成的應力集中問題。圓柱殼開孔問題，國內外學者做了大量的研究。SangEuilee 等[1]用有限元方法探究了在開孔后的殼體的極限強度問題。Talezadehlari 等[2]研究了復合材料圓柱殼開孔加強的問題。朱邦俊和王玉華[3]對帶有開孔的薄壁圓柱殼進行了有限元分析，得到了開圓孔的薄壁圓柱殼的應力特性。許兵[4]對切斷一根肋骨的用圍壁加強的正交單圓孔進行了分析。施濤[5]研究了典型耐壓船體開孔加強結構并進行了優化分析。周猛猛[6]對圍壁加強的圓柱殼開孔結構進行了有限元分析。舒斌[7]用Ansys 軟件建立了大開孔圓柱殼采用圍壁補強的模型，用2 倍斜率法確定其極限載荷值。Obodan 等[8]研究了薄壁圓柱殼非線行與穩定性。Aninash R. Kharat 等[9]研究了不同形式的加強構件對于加強件以及孔邊應力的影響，針對4 種加強構件的設計方式詳細分析了不同的加強構件對應力產生的影響。張錦嵐[10]采用參數化建模方式，討論了多參數對于開孔周圍應力的影響。

對于單殼體的水下航行器，開孔只能采用“單邊圍壁”加強方式，即孔口圍欄外伸段極短（或缺失），確保圍欄不突出于殼體外，這種極端非對稱圍壁加強結構不僅改變了傳統開孔區應力特性，并使空口應力場復雜化，而且大大削弱了加強效果，嚴重影響開孔強度。

目前針對單邊加強技術研究較少，基礎比較薄弱，因此研究非對稱開孔加強具有重要意義。本文針對典型的圓柱殼結構，通過數值分析的方法，探究圓柱殼開孔非對稱加強的變化規律，為以后設計提供參考。

1 數學模型

1.1 幾何模型

圓柱殼模型如圖1 所示。2 種顏色代表2 種不同剛度材料（材料參數見表1）。兩端部設置過渡段以及封板（這部分的設置主要是模擬試驗過程中的邊界條件，封板用于密封，過渡段用于消除封板對殼體邊界應力的影響，其剛度大于殼體剛度）。

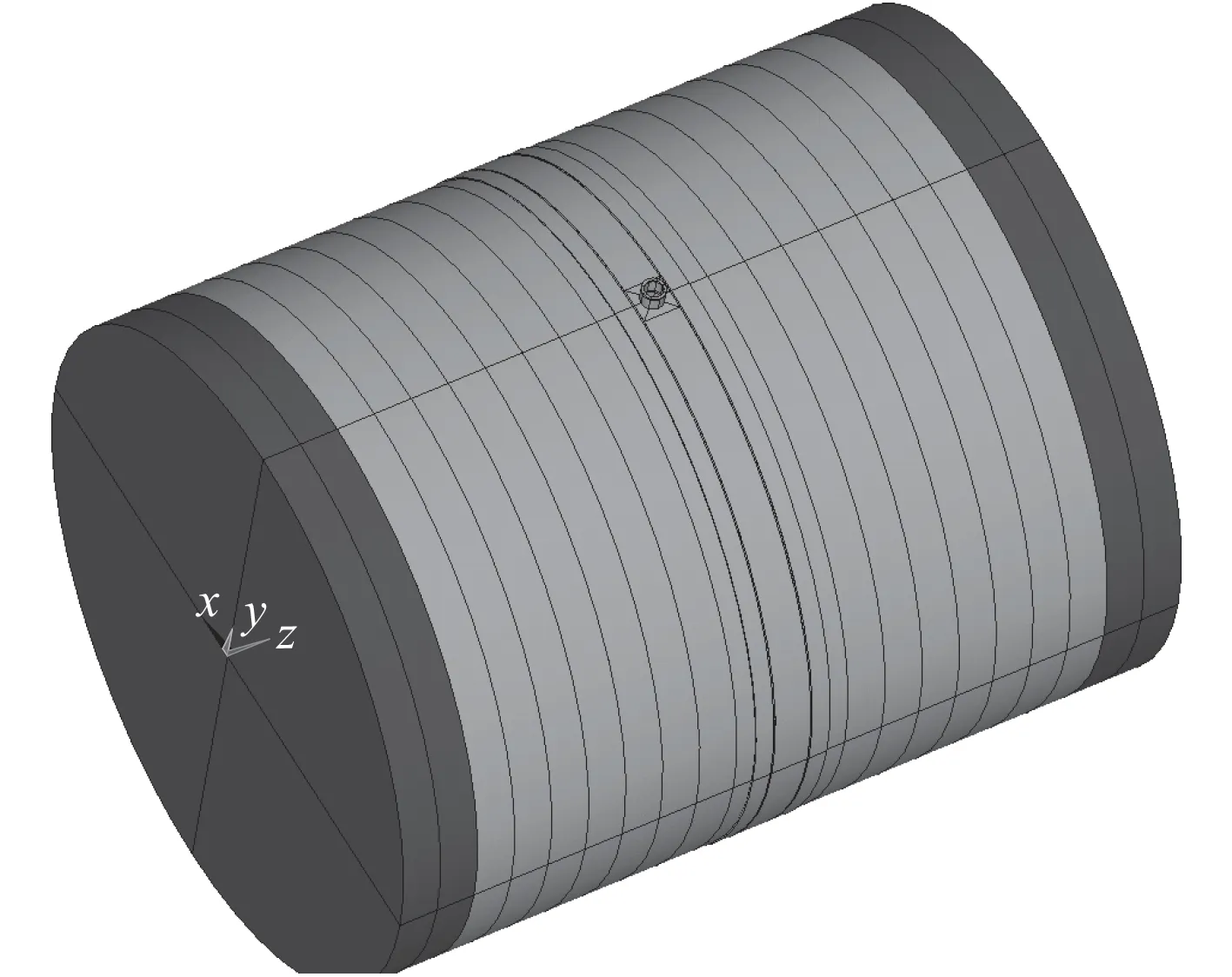
圖 1 圓柱殼幾何模型Fig. 1 Geometric model of cylindrical shell

表 1 圓柱殼材料參數Tab. 1 Parameters of material

圓柱殼模型相關尺寸進行了無因次化處理，具體如表2 所示。

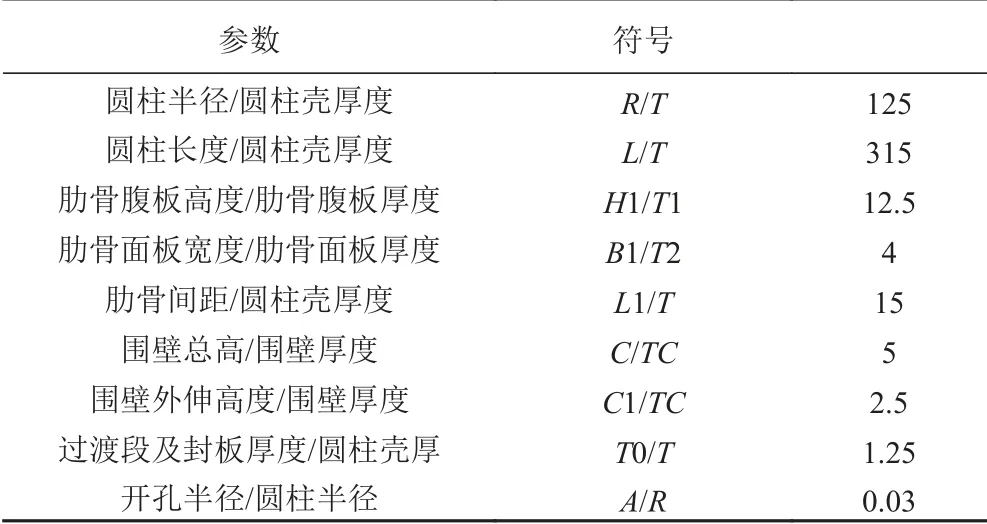
表 2 圓柱殼幾何參數Tab. 2 the parameters of the cylindrical shell

1.2 有限元方法

計算模型網格采用體-殼結合的形式，在開孔附近區域采用體網格，在其余部分采用殼網格。體網格與殼網格之間采用MPC 單元連接。這樣做既能夠提高計算的準確性，又不至于導致大量的計算。MPC 單元提供了一個極為有效的接觸模擬算法，能夠很好實現殼體和實體的綁定約束。

邊界條件為：Z=0（U X=0，U Y=O，U Z=0，RTOX=0，RTOY=0，RTOZ=0）：z=L（UX=0，UY=O，RTOX=0，RTOY=0，RTOZ=0。耐壓體上加載的壓力為6.75 MPa，加載及邊界條件示意圖如圖2 所示。

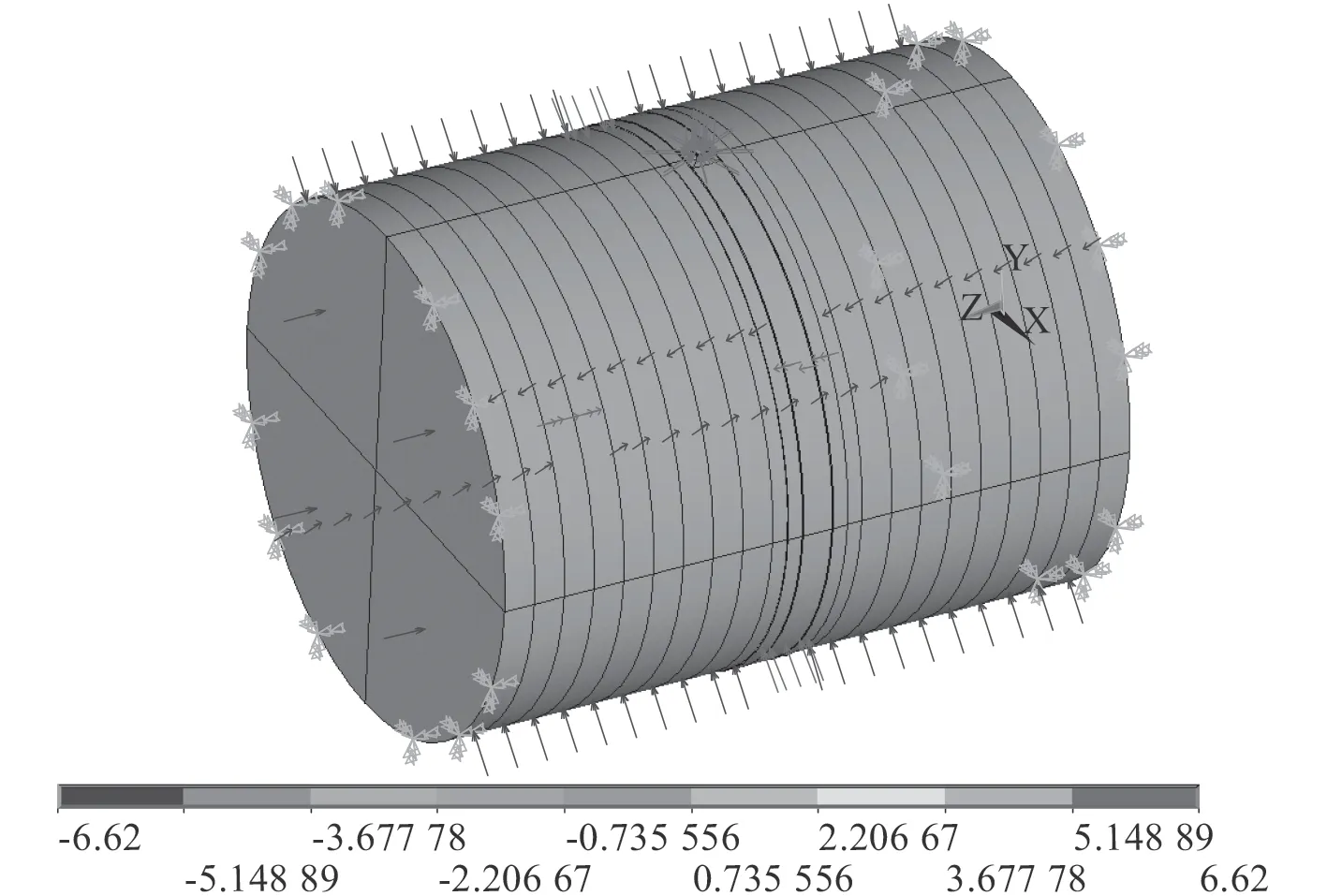
圖 2 圓柱殼邊界條件以及加載情況Fig. 2 Boundary condition and the pressure of the cylindrical shell

有限元網格總量為218 685（包括MPC 單元），其中體網格、殼網格以及MPC 單元的數量分別為17 627，34 886，7 520。

圖 3 圓柱殼網格示意圖Fig. 3 Mesh of the cylindrical shell

圖 4 加強圍壁網格示意圖Fig. 4 The mesh of the enclosing wall

2 數值模擬結果分析

2.1 對稱圍壁高度變化對孔口應力的影響

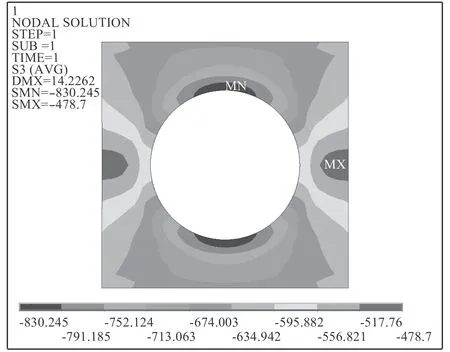
圖 5 孔邊殼板應力分布Fig. 5 Stress distribution of the shell around opening

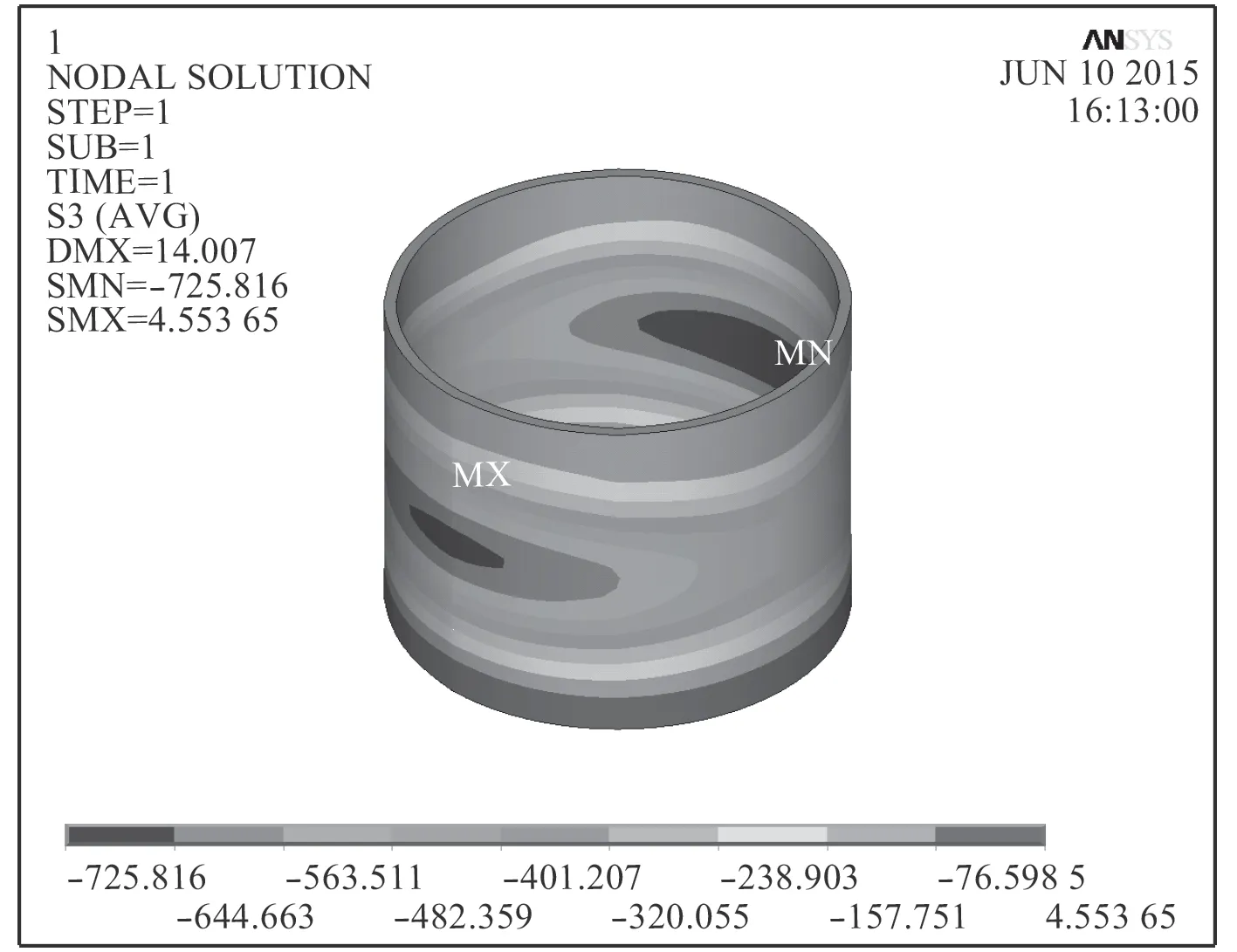
圖 6 圍壁應力分布Fig. 6 Stress distribution of the enclosing wall

開孔周圍殼板的應力分布如圖5 和圖6 所示。應力的最大值發生在圍壁與殼板的相貫線處。圖7 和圖8 的計算結果表明。對于開孔的對稱圍壁加強，不同的開孔半徑，應力水平不同，半徑越大，孔邊的應力水平越高：R200＞R160＞R135。隨著圍壁高度的增加，孔邊應力不斷地減小，減小的趨勢先快后慢，最后趨于某一個值，這個值通常稱為圍壁的“有效高度”。一般來說，有效高度是指在這個高度范圍內，圍壁的增長能有效減少孔邊應力集中的現象，一旦超過此高度范圍，圍壁的增長不再有效。

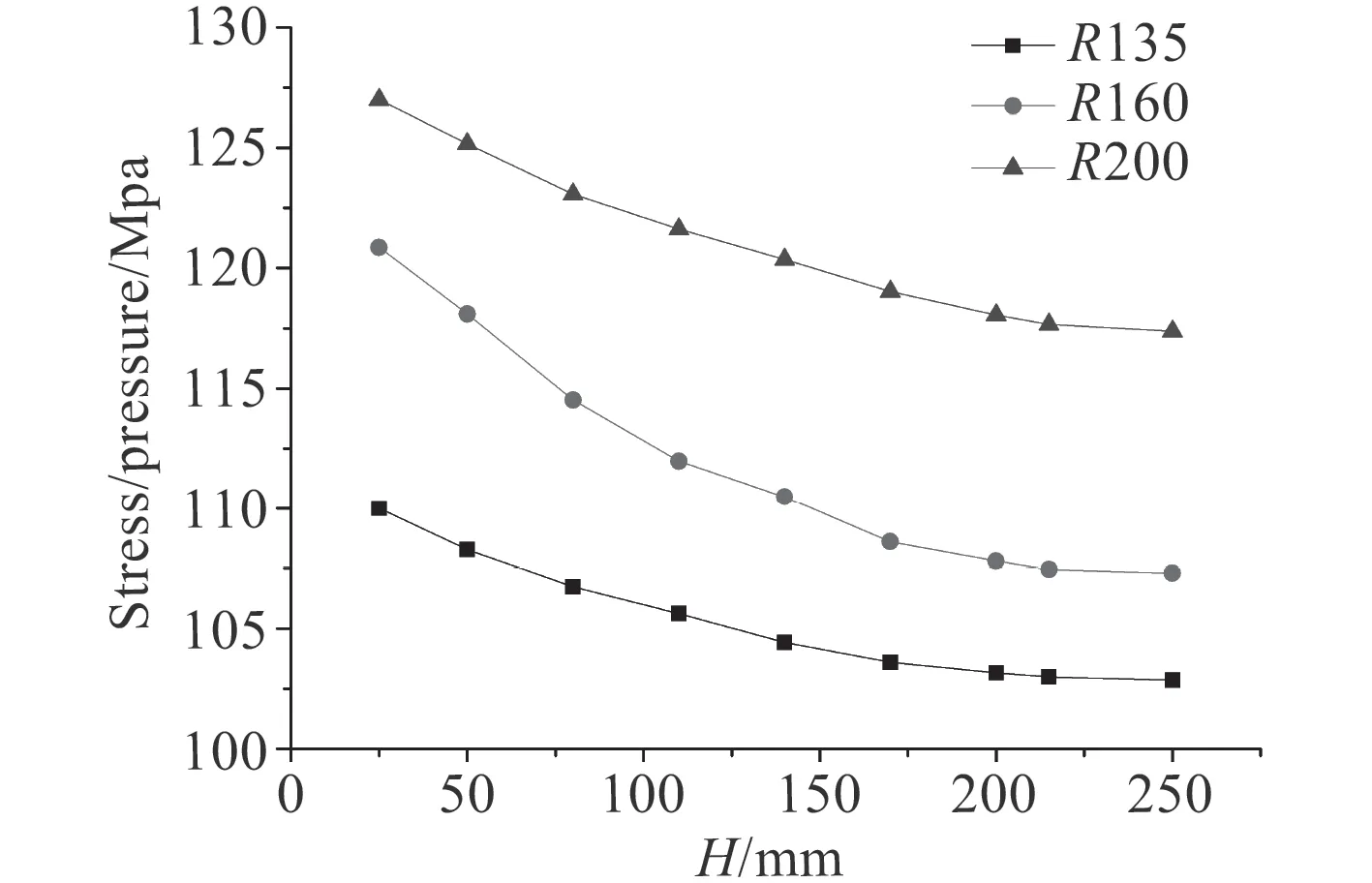
圖 7 孔邊殼板應力載荷比隨圍壁高度變化示意圖Fig. 7 Stress on the shell around the opening

當壓力作用在耐壓圓柱殼上的時候（見圖9），圍壁將會在壓力的作用下發生變形，圖中A 點處的應力將會因此而增加，因此最大應力值發生在圍壁與殼板的相貫線處，圍壁的變形隨遠離相貫線處而減小，因此應力水平也逐漸減小。

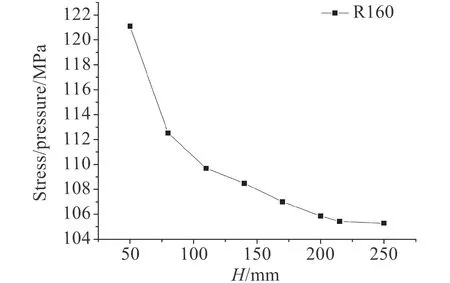
圖 8 圍壁應力載荷比隨圍壁高度變化示意圖Fig. 8 Stress on the enclosing wall

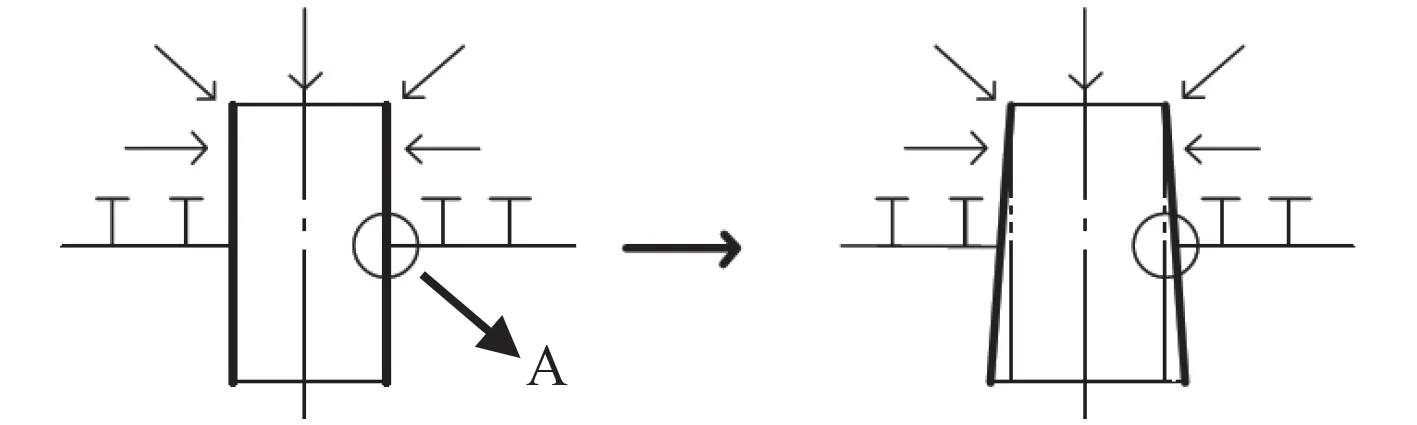
圖 9 圍壁在載荷下的變化示意圖Fig. 9 Variation of the enclosing wall under the pressure load

2.2 非對稱圍壁高度變化對孔口應力的影響

對于單殼體水下航行器來說，相比雙殼體，其幾何形狀受到限制，為了保證航行器外形線光順，只能采用單殼體加強的方式來進行開孔補強。單邊加強的孔口應力狀況將更加復雜，規律是否與對稱加強一致，是需要進行探究的問題。

圖10～圖12 分別為在固定圍壁外長為50 mm，100 mm，125 mm 的情況下，只改變圍壁內長的Ansys有限元計算結果，圖中的取值為殼板開孔處同一點的應力值。對于不同的固定圍壁外長以及不同的開孔半徑而言，開孔邊緣的殼板應力隨著圍壁內長的變化呈現出相似的趨勢。隨著圍壁內長的增加，應力集中逐漸減小，最后趨于一個穩定值。這說明圍壁內長達到了“有效高度”，這與之前對稱圍壁補強的趨勢類似。

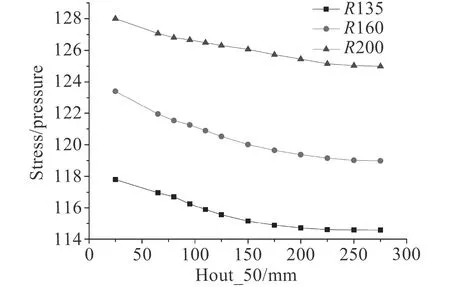
圖 10 外伸圍壁高度為50 mm 時隨著圍壁內高增加孔邊殼板應力變化示意圖Fig. 10 Height of the enclosing wall above the shell is 50 mm

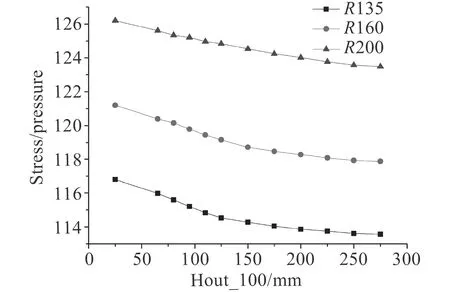
圖 11 外伸圍壁高度為100 mm 時隨著圍壁內高增加孔邊殼板應力變化示意圖Fig. 11 Height of the enclosing wall above the shell is 100 mm

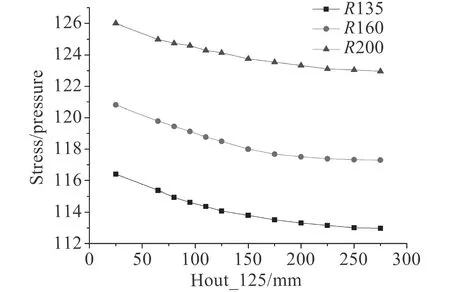
圖 12 外伸圍壁高度為125 mm 時隨著圍壁內高增加孔邊殼板應力變化示意圖Fig. 12 Height of the enclosing wall above the shell is 125 mm

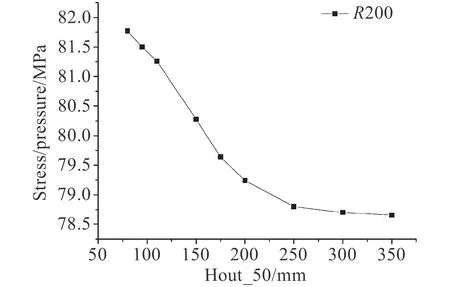
圖 13 外伸圍壁高度為50 mm 時隨著圍壁內高增加圍壁應力變化示意圖Fig. 13 Stress on the enclosing wall

圖13 為與殼板邊緣對應的圍壁上的同一處的應力取值。該曲線為開孔半徑為200 mm 圍壁外長固定50 mm時的應力值變化趨勢圖，作為對比參照可見，同一點處不論是圍壁還是殼板上的應力都是隨著內長的增加而減小最后趨于穩定。

當圍壁內長固定，只改變外長的情況下，開孔邊緣殼板的應力變化（見圖14）以及圍壁上同一點應力的變化趨勢（見圖15）仍然表現為：隨著圍壁外長的增加，應力集中減小，最后應力值趨于某一個穩定的數值，說明此時圍壁達到了其“有效高度”。實際上，固定圍壁內長不斷增加圍壁外長的情況，在工程中并不會常遇到，因此該規律僅作參考。

2.3 非對稱圍壁厚度變化對孔口應力的影響

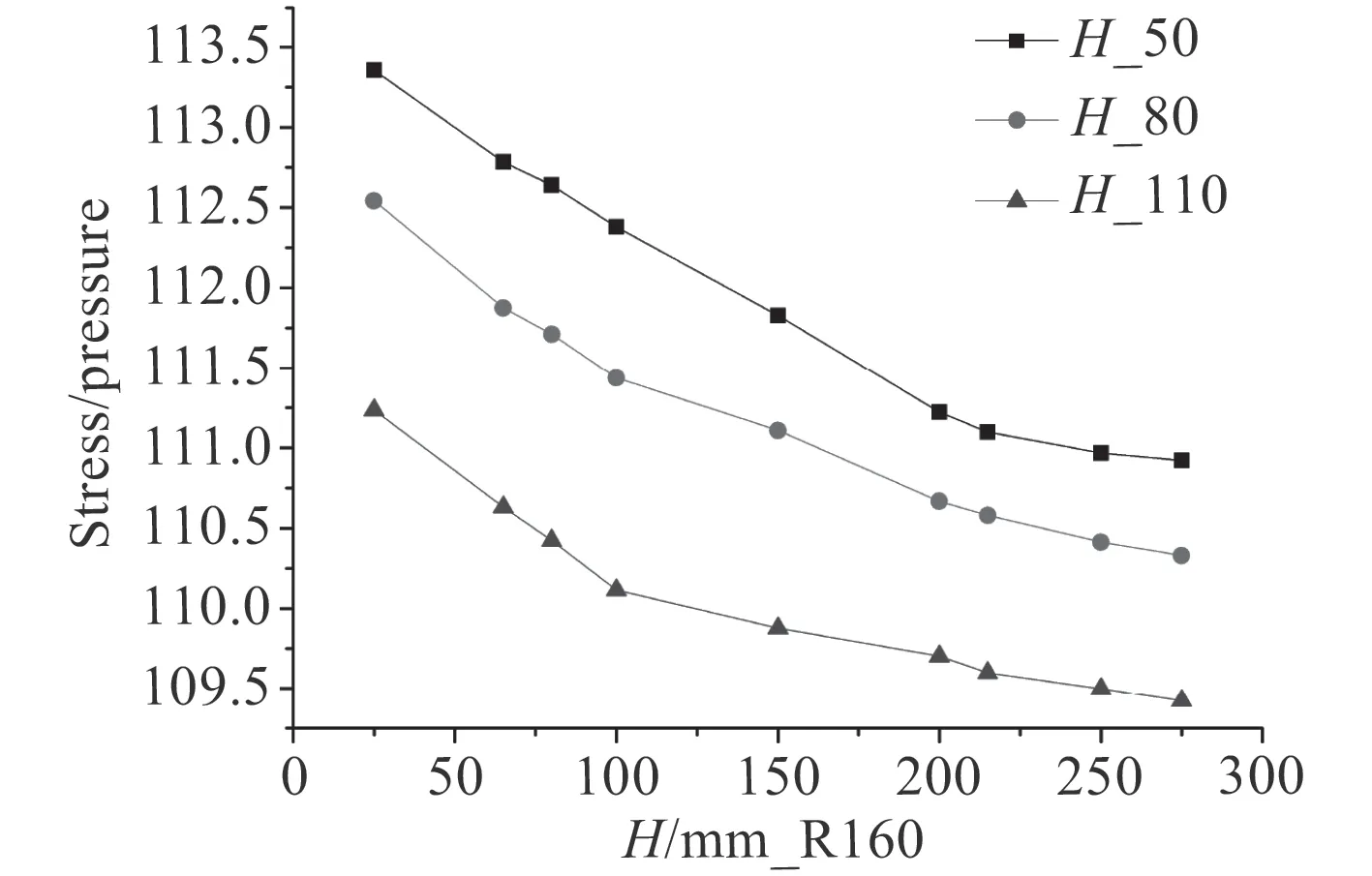
圖 14 圍壁內伸高度為50 mm 時隨外伸高度變化孔邊殼板應力變化示意圖Fig. 14 Height of the enclosing wall inside the shell is 50 mm

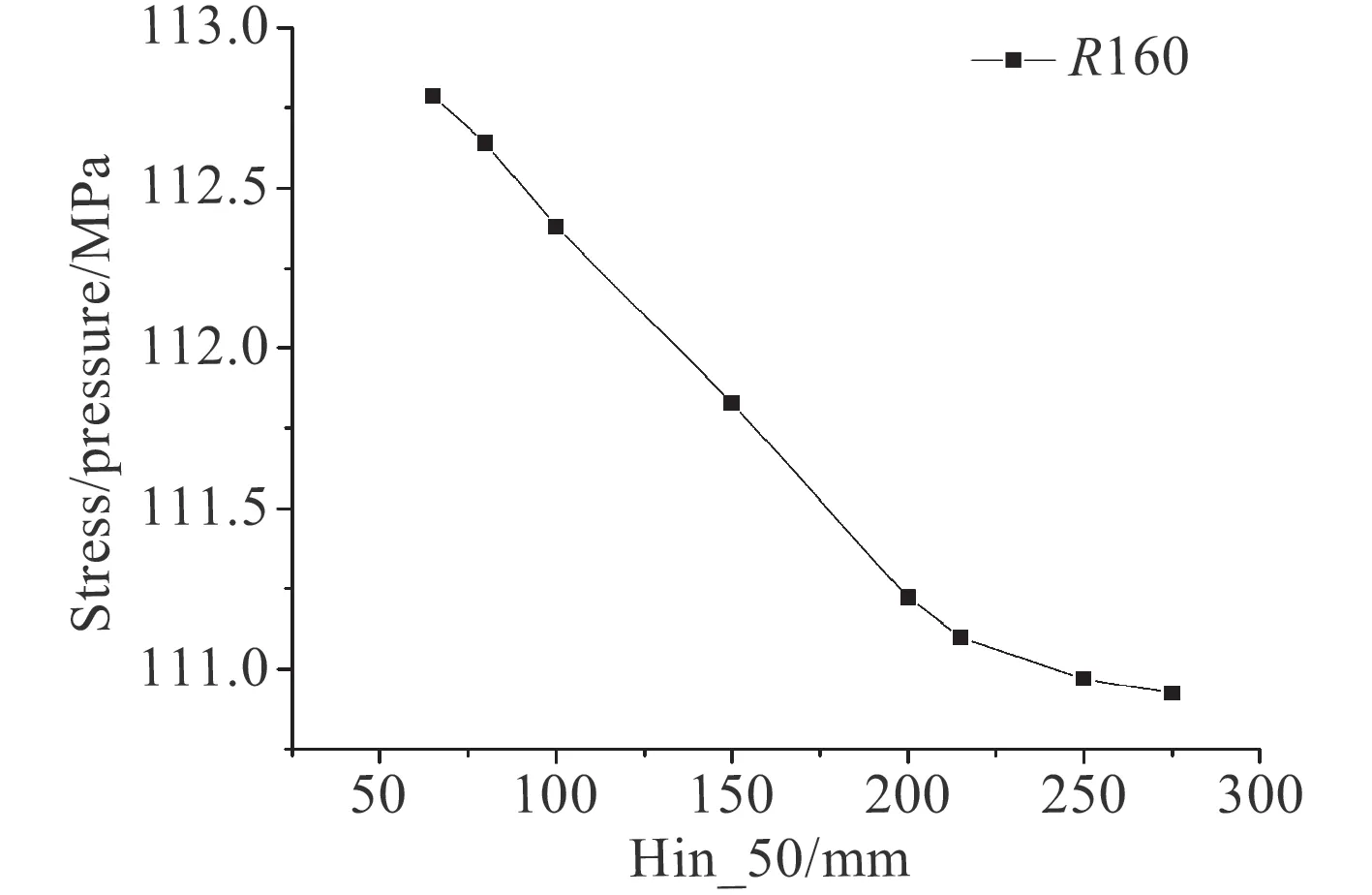
圖 15 圍壁內伸高度為50 mm 時隨外伸高度變化圍壁應力變化示意圖Fig. 15 Stress on the enclosing wall

前文中提到，圍壁的高度是不能夠無限延長的，它最終會達到一個“有效高度”，在此高度范圍之外，無論高度再怎么變化，對于應力的改善不再有明顯的效果。因此，對于非對稱圍壁，保持其他變量一定，探究增加圍壁厚度對孔口應力的影響。圖16 為計算時孔邊殼板的應力分布，計算結果如圖17 和圖18所示。隨著圍壁厚度的增加，孔邊殼板處的應力值減小，最后趨于穩定值。這說明圍壁的厚度存在一個類似“有效高度”的“有效厚度”，在“有效厚度”的范圍內，增加厚度能有效改善孔邊應力集中現象，當厚度超過這一值，增加厚度將不再有明顯的效果。圍壁的應力值變化如圖19 所示。隨著厚度的增加，圍壁應力變化不斷減小并趨于平緩，說明圍壁厚度的增加對于殼板以及圍壁的應力改善都有較為明顯的效果。

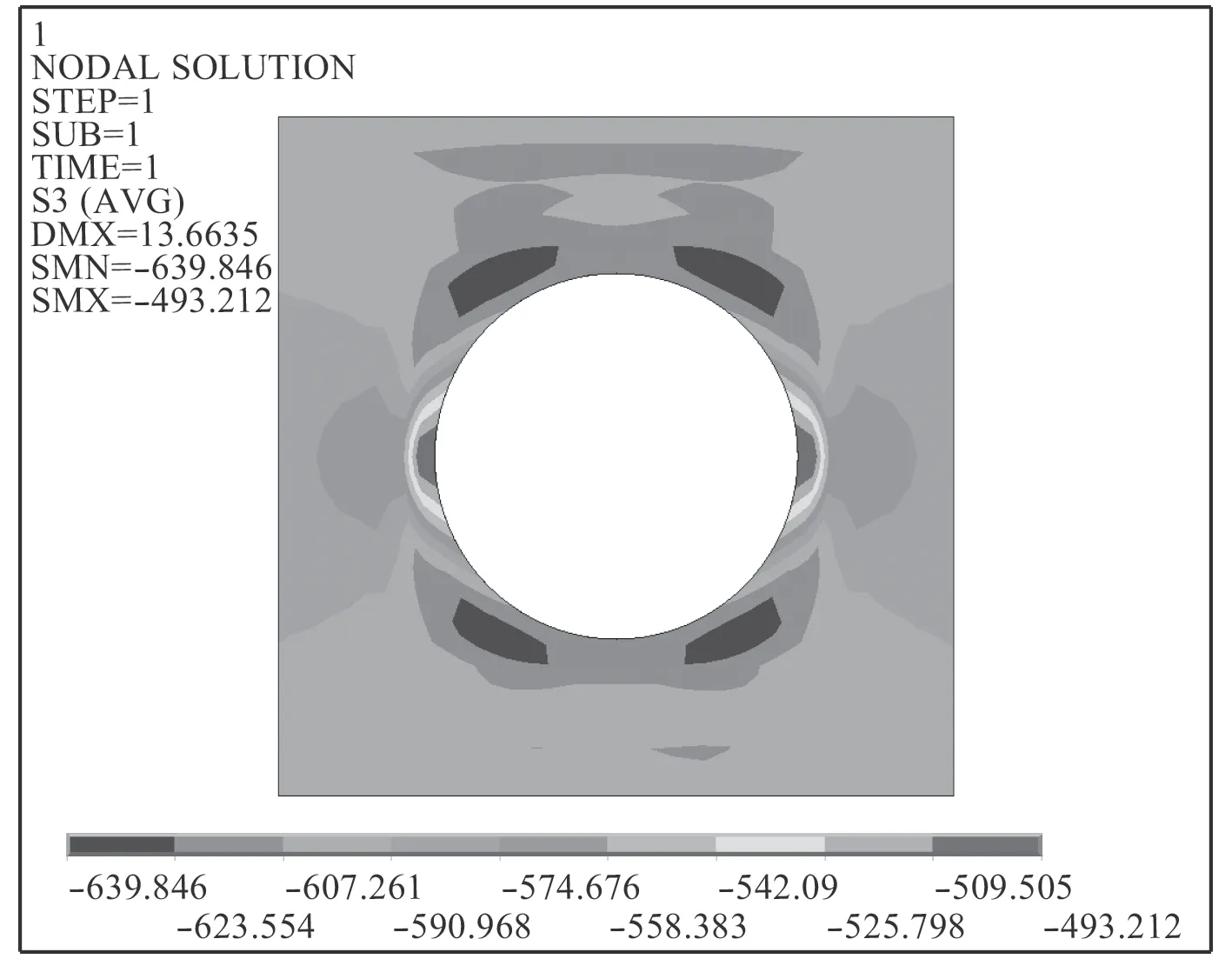
圖 16 開孔周圍殼板應力分布（圍壁厚度=40 mm）Fig. 16 Stress distribution of the shell around opening（thickness=40 mm）

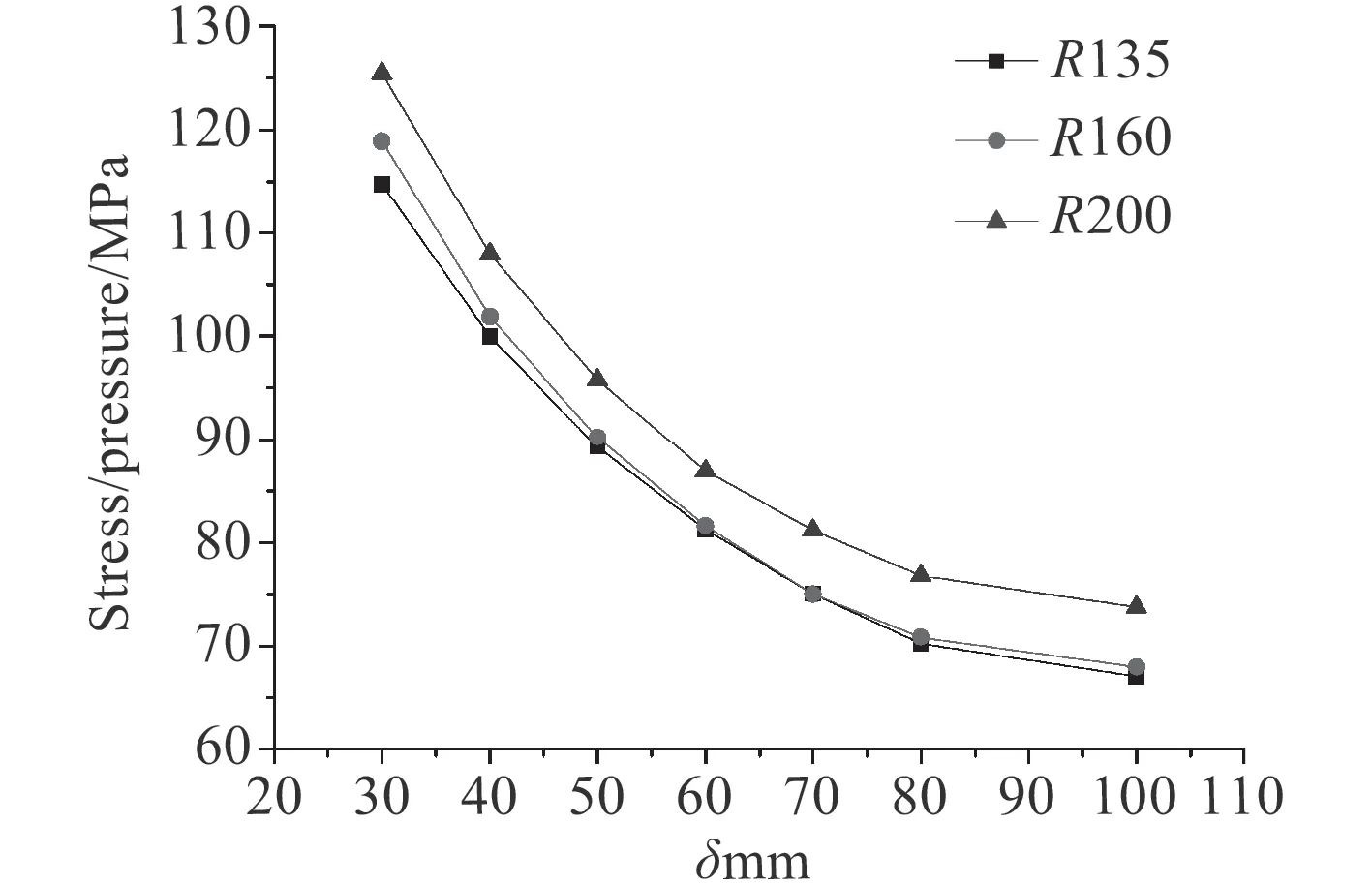
圖 17 應力載荷比隨著圍壁厚度增加變化示意圖（不同曲線代表不同半徑）Fig. 17 Stress varies with different thickness

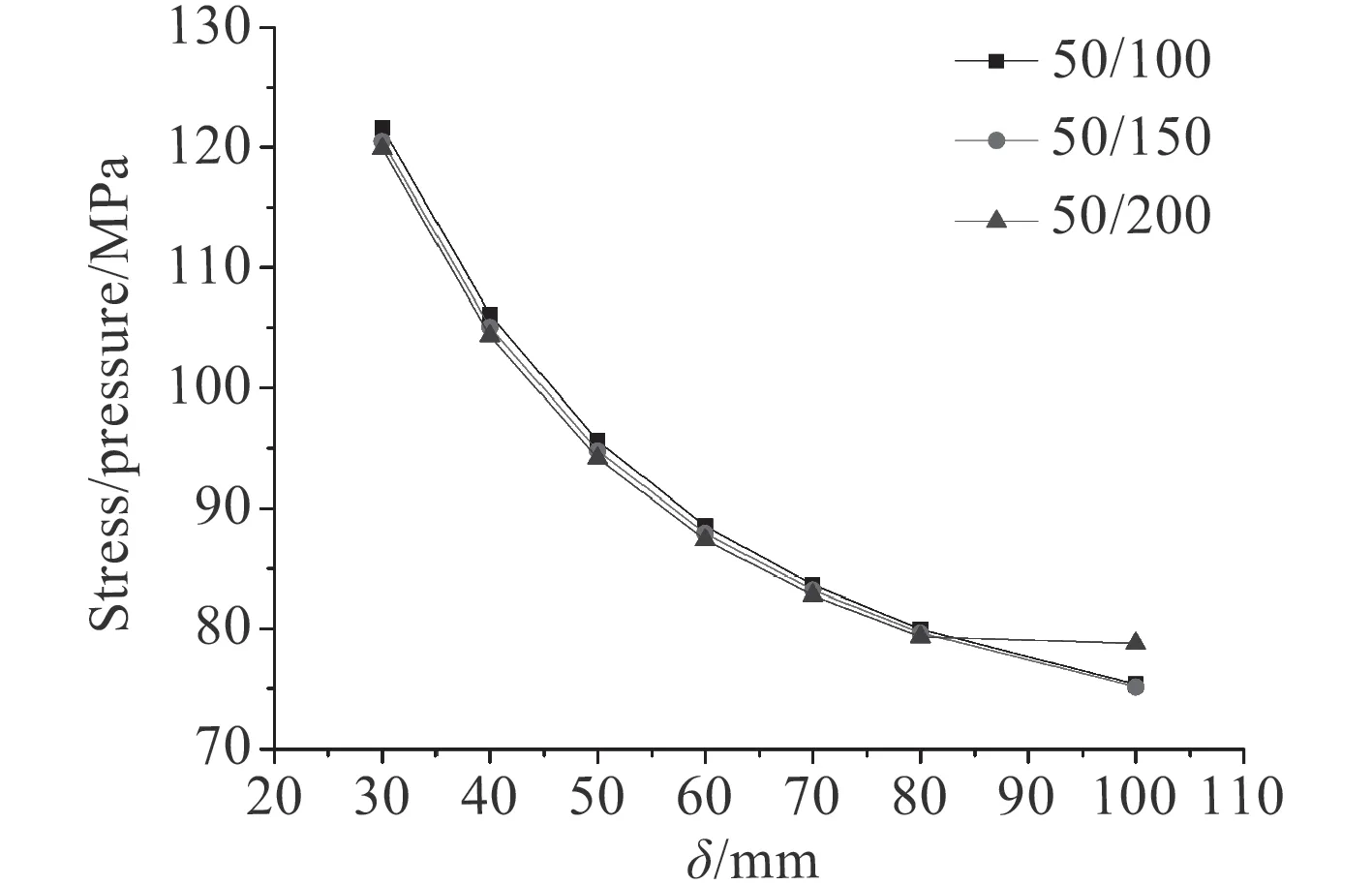
圖 18 應力載荷比隨著圍壁厚度增加變化示意圖（不同曲線代表外伸高度為50 mm 時不同內伸高度下厚度變化趨勢）Fig. 18 Stress varies with different thickness（different height inside the shell）

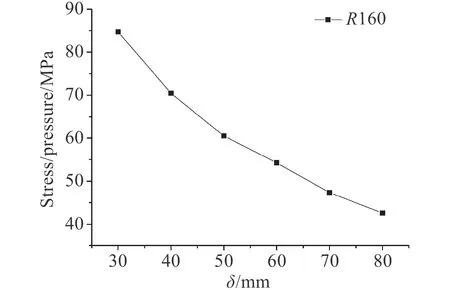
圖 19 厚度變化時圍壁應力變化趨勢示意圖Fig. 19 Stress on the enclosing wall for different thickness

3 有限元數值解

通過對單殼體非對稱圍壁補強的研究，得出以下幾點結論：

1）基于數值分析的結果，不論是對于對稱的圍壁補強，還是非對稱的圍壁補強，隨著高度或者厚度的增加，孔邊殼板的應力值都會減小最后趨于一個穩定值，這個值稱為“有效高度”或者“有效厚度”。因此在進行圍壁補強設計時，應首先找到有效高度值，在有效高度范圍內再根據具體要求進行調整設計。

2）對于單殼體水下航行器，其受幾何形狀限制，只能采用單邊加強的方式進行補強，孔口的應力場將更加復雜，其加強規律是非常值得探究的。本文計算結果表明，對于非對稱圍壁的開孔補強，不論是開孔邊緣的殼板上的應力還是圍壁上的應力，隨著圍壁高度（厚度）的增加，其值都會減小最后趨于穩定。但是對于非對稱而言，“有效高度’的值通常會比對稱的圍壁補強的大一些。原因在于單邊加強相比較對稱加強，由于圍壁外伸出殼體的長度受到限制，高度通常較小，大大減弱了加強效果，因此需要更長內伸的圍壁來彌補缺失的效果。

3）當圍壁的高度達到了“有效高度“之后，增加圍壁的厚度往往能夠繼續減小孔邊的應力集中。因此在進行非對稱圍壁補強件設計時，綜合考慮高度與厚度的值，進行優化能夠最大限度的達到理想的效果。

本文重點研究單殼體水下航行器的開孔非對稱圍壁補強，進行一系列的數值仿真分析。結果表明，非對稱與對稱的圍壁補強在減小孔邊應力集中的問題上，應力隨著圍壁變化而變化的趨勢大致相似，但是具體數值有一定的區別。今后，將探究采用非對稱圍壁開孔加強結構圓柱殼的穩定性問題；切斷肋骨情況下，采用非對稱圍壁加強的圓柱殼強度、穩定性等問題。