輪對系統隨機動態分叉研究

張 波 朱海燕 曾 京 蔣忠城 陳清化

(1.中車株洲電力機車有限公司 試驗檢測工程中心,湖南 株洲 412001;2.大功率交流傳動電力機車系統集成國家重點實驗室,湖南 株洲 412001;3.華東交通大學 機電與車輛工程學院,江西 南昌 330013;4.西南交通大學 牽引動力國家重點實驗室,四川 成都 610031;5.湖南鐵路科技職業技術學院,湖南 株洲 412000)

車輛蛇行運動是軌道車輛獨有的現象,由于車輪踏面近似為錐形,輪對運行時會發生橫向擺動,同時伴隨有繞其質心的垂直軸來回搖頭轉動,運動軌跡類似“蛇”爬行過程的波形。蛇行運動存在臨界失穩點,正常情況下輪對系統會在蠕滑力作用下自動對中,但一旦越過臨界失穩點蛇行運動就會失控,輪軌蠕滑力不足以使輪對對中,輪對發生蛇行運動,橫向運動加劇,車輛振動平穩性和運行安全性將嚴重變差,甚至有發生脫軌和翻車的可能,可以說蛇行運動是決定車輛能否高速運行的關鍵因素。

車輛出現蛇行失穩的臨界狀態對應的速度稱為蛇行失穩臨界速度,為了獲取準確的臨界速度,學者們將穩定性和分叉理論引入蛇行運動問題中,建立了精細化的動力學模型,提出了許多定性以及定量的研究方法。曾京[1]和呂可維[2]分別運用打靶法和延續算法對非線性車輛蛇行運動Hopf分叉現象進行了數值求解,對輪對蛇行運動中的極限環性質進行準確判別,可精準求解出非穩定的虛環,解決了龍格-庫塔法求解不穩定極限環的困難。丹麥True[3]教授借助延續算法軟件包PATH 對非線性鐵道車輛系統的穩定性與分岔問題進行了深入討論,取得了較為典型的理論性成果。Polach[4]結合鐵道車輛蛇行運動理論與試驗研究,詳細對比分析了幾種標準常用的構架失穩評判標準的差異,指出車輛穩定性的計算結果除了依賴于車輛結構參數之外,與輪軌接觸關系和數值計算方法也有關聯。高學軍研究了客車不對稱分岔行為[5],創新性地提出“合成分岔圖”的概念和構造方法。

但是上述這些研究都是在確定域中進行的,均沒有考慮隨機激擾的影響,這僅僅是理想情況下的理論分析,判定車輛系統是否失穩通常都是基于系統部件橫向振動的衰減特性,但實際車輛線路運行時,由于持續存在隨機激擾,車輛振動響應曲線不會出現明顯的收斂或發散特征,此時確定性框架下的理論失穩判定方法不再適用,已經不能滿足高速車輛的穩定性分析需求。我國對于線路運行過程中的車輛失穩判定方法:對軸箱彈簧正上方對應的構架位置橫向加速度進行10 Hz低通濾波,若該橫向加速度峰值出現連續6次達到或超過極限值0.8g時,則判定轉向架橫向蛇行失穩。但這一方法并無理論根據,且由于我國列車運行環境、運行速度與國外的巨大差異,因此并不具備廣泛適用性。盡管也有許多學者提出了新的判定方法[6-8],但都有各自的局限性。

大量研究發現,隨機激擾和非線性會出現相互耦合關系,兩者的耦合效應激發了激擾在非線性系統中的作用,這種作用在系統響應演化過程中具有決定性且不可控。基于這一前提,我們需要跳出穩定域框架,在隨機域中尋求新的突破,聚焦于對自然規律的描述更為本質和真實的隨機系統,探討隨機激擾對車輛動力學動態行為的影響,從機理上分析車輛隨機振動響應,研究隨機振動響應的內在非線性特性及變化規律,為軌道車輛系統安全性能設計提供理論指導價值,在高鐵全面飛速發展的大背景下,這也是大勢所趨。

目前關于車輛隨機穩定性的研究較少,比較典型的研究為劉偉渭等[9-10]和張波等[11-13]的研究工作,但這些研究工作都是基于超臨界輪對系統,對亞臨界系統的隨機穩定性并未做研究。本文在此基礎上,進一步深入研究隨機參激下亞臨界和超臨界分叉2種輪對系統的隨機穩定性及隨機分叉,分析隨機激擾對穩定性的影響,對比2種類型輪對系統的隨機分叉的差異,探討車輛隨機系統的失穩判定方法,研究隨機臨界速度的計算方法。此外,本文關注的重點在于隨機激擾的影響,關于其他車輛參數的影響,已有大量研究,本文不做討論。

1 懸掛輪對系統隨機動力學建模與求解

1.1 模型建立

軌道車輛結構龐大,自由度較多,其非線性問題非常復雜,如果再考慮隨機影響,問題的復雜度將劇增。在車輛系統研究過程中,通常根據研究需要對車輛模型進行適當簡化,對于重點關注項點精細建模,對于非重點關注項點可做適當簡化。為了簡化理論研究的難度,本文選取自由度較少的懸掛輪對橫向動力學模型來作為分析對象。

建模過程中可作如下基本簡化[14]:

(1)構架與輪對之間的耦合效應可忽略,構架的搖頭以及側滾運動對輪對的影響可忽略。

(2)由于輪對側滾與橫移的耦合效應,僅考慮輪對搖頭和橫移2個自由度。

(3)不考慮輪對柔性,不考慮車輪與鋼軌脫離情形。

(4)暫不考慮一系懸掛的非線性特性,僅考慮輪軌間非線性特性。

(5)車輪踏面外形采用經典的錐形踏面。

輪對系統建模時采用Kalker經典線性輪軌蠕滑理論,輪軌非線性接觸關系可近似處理為一個非線性五次多項式,對應的2個非線性項系數α1、α2的選取依據來源于文獻[14]。車輛系統的隨機激擾主要包括隨機外激和隨機參激,前者主要包括氣動隨機激擾以及輪軌隨機激擾,后者主要是由于自身結構的隨機特性引起的激擾。目前商用動力學仿真軟件很容易實現外部激擾對車輛穩定性的影響分析,但是關于隨機參激激擾的研究則鳳毛麟角,商用軟件也無法考慮參激激擾的影響,因此本文側重于研究隨機參激對穩定性的影響,且此方法仍然適用于隨機外激。

實際車輛中,隨機參激也是無處不在的,車輛實際參數值和理論設計值通常會有一定差別,這一差別往往是隨機不可控的,而車輛系統一系懸掛參數對運動穩定性的影響較大,因此研究一系懸掛參數的隨機變化對車輛穩定性的影響意義重大。

實際上由于材料及結構的制造誤差,橡膠元件的老化以及懸掛元件的頻變特性都會引起參數的隨機變化,由于這些因素具有隨機性,無法準確描述其特性。為了描述參數的隨機性,通常的做法是結合大批量相應部件試驗結果統計分析參數分布規律,這種分布規律通常是參數理論值與一個隨機過程的疊加效應,這一隨機過程模型就是本文所說的隨機參激。鐵道車輛輪軌隨機激勵屬于強隨機激擾,主要呈現非高斯分步,而車輛一系懸掛參數的隨機激擾相對較弱且接近于高斯分布,因此工程分析時可近似處理為高斯白噪聲隨機激擾。這種方法有兩大優勢:(1)可直接應用成熟的高斯白噪聲數學理論;(2)高斯白噪聲數學模型有利于理論分析,簡化理論分析難度。因此,本文選取高斯白噪聲經典隨機過程來模擬輪對系統的一系隨機參激,高斯白噪聲的最鮮明特點是功率譜密度為常數且功率是無窮大。軌道車輛輪對系統搖頭和橫移耦合的隨機幾何模型示意圖見圖1。

圖1 輪對幾何模型示意

相關函數為

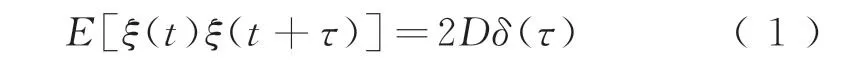
式中:v為車輛運行速度;ξ(t)為高斯白噪聲隨機參激激擾,該隨機過程均值為0;2D為強度。

由圖1關系,可建立輪對橫移和搖頭運動耦合方程。

(1)輪對橫移運動

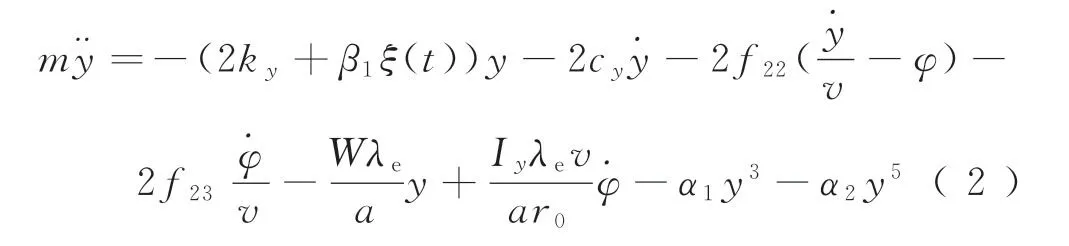
(2)輪對搖頭運動

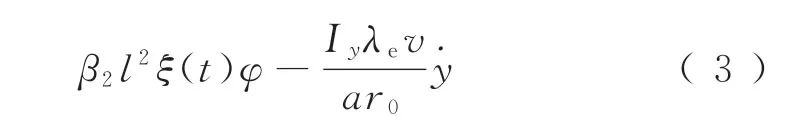
軌道車輛及輪對系統中的Hopf分叉有2種常見類型:超臨界和亞臨界分叉,為了研究這兩類系統的隨機動力學行為差異,分別選取2組輪對系統參數作為代表,各參數取值及物理意義詳見表1。關于隨機項控制系數β1和β2的選取,實際應用時可以通過部件大批量抽樣試驗統計激擾的能量來確定控制參數,本文的參數取值僅僅只是一個示例,并不精確。

表1 兩類輪對系統參數

上述輪對系統的運動方程表示成矩陣形式,即

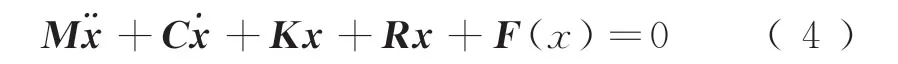
式中:

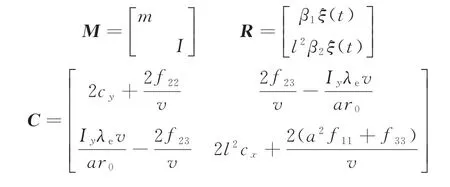
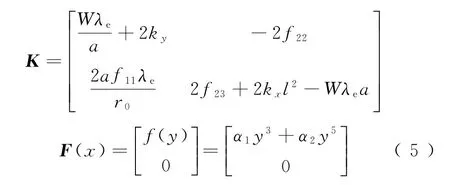
1.2 輪對系統的隨機平均求解

方程(4)是隨機微分方程,其求解比較復雜,許多學者針對具體問題提出了相應的求解方法[15]并取得了很好的效果,但都不具備很好的推廣性。相對來說,隨機平均法應用最為廣泛,隨機平均法實際上是隨機意義上的Krylov-Bogoliubov-Mitropolsky(以下簡稱KBM)漸近法,許多學者進行了大量關于隨機平均法的研究,最為典型的就是浙江大學朱位秋院士的成果,朱院士在Hamilton框架下建立了一套完備的擬Hamilton系統的隨機平均法理論體系[16],可快速求解非線性系統的隨機響應,進而分析隨機穩定性與隨機分叉等問題。

相比于能量和位移幅值,位移和速度隨時間的變化速率明顯更快,也就是說能量和位移幅值屬于慢變過程,而速度和位移屬于快變過程。由于慢變過程體現了系統長時間歷程內的性態,在研究中應重點關注。隨機平均求解的基本原理就是將快變過程隨時間變化的特性在時間域進行平均,從而將系統簡化為關于慢變過程的隨機平均方程。隨機平均法主要有以下兩大優勢:(1)可對系統降維簡化問題的復雜度;(2)系統降維簡化信息不失真,可保留原系統的主要非線性特性。本文通過隨機平均法將輪對橫向位移和速度等快變過程組成的多維空間域映射成關于系統能量等慢變過程的一維域。

取廣義位移q1=y,q2=φ,p1=,p2=,將輪對運動方程轉化為如下形式

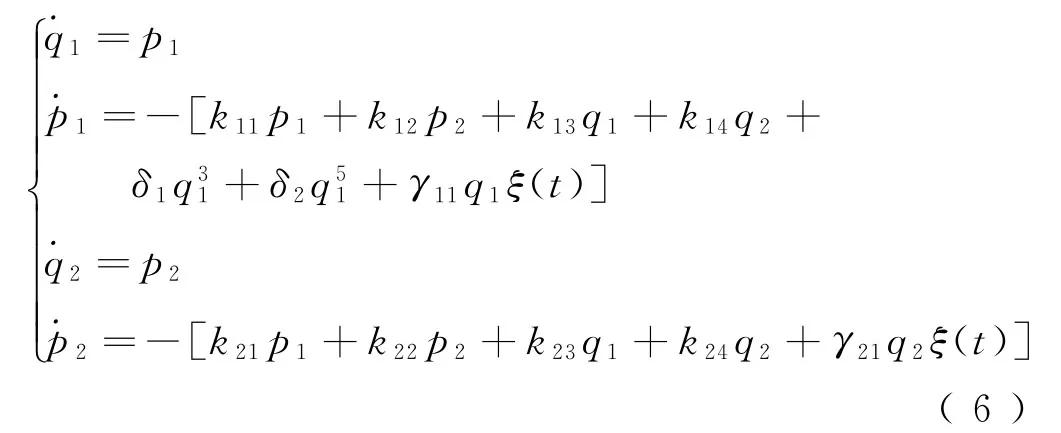
該輪對系統中,由于陀螺力[17]的存在,導致輪對系統變為非保守系統,鑒于陀螺項的反對稱性,可取系統的Hamilton函數為

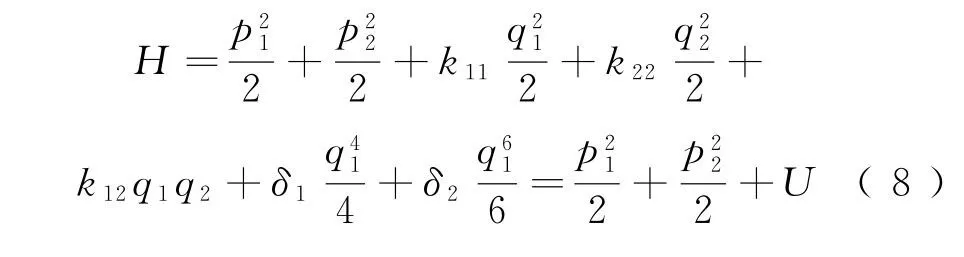
式中:H為對應輪對系統的廣義能量。

依據隨機平均法,式(6)可轉化為It?(伊藤)隨機微分方程

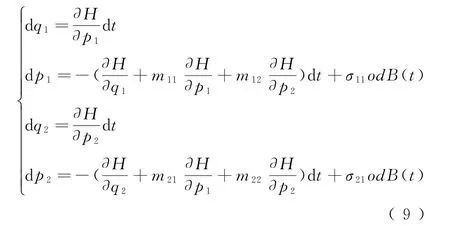
式中:odB(t)表示隨機積分,且

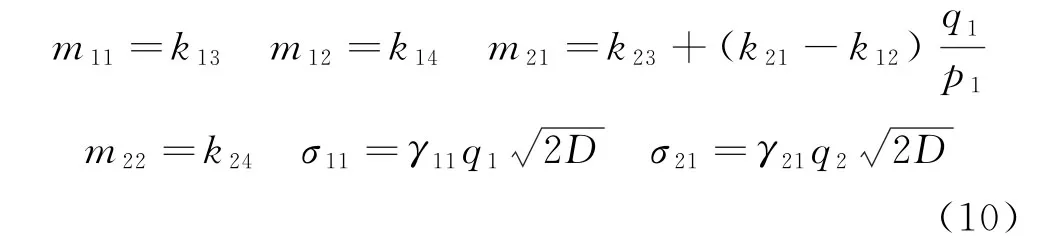
根據Hamilton系統理論分類[18],該輪對隨機系統屬于擬不可積Hamilton系統,利用擬不可積Hamilton系統隨即平均法對位移和速度等快變過程進行隨機平均,可得關于慢變過程能量H(t)的It?隨機平均微分方程

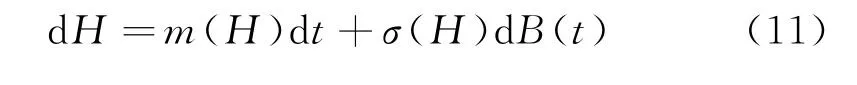
式中:

其中,

且R滿足

2 輪對系統的隨機穩定性與隨機分叉

2.1 輪對系統Hopf分叉

當不考慮隨機激擾時,即輪對系統(4)中隨機項滿足R=0。本文根據表1中的參數采用打靶法[1]分別求解兩類輪對系統橫向位移的Hopf分叉及極限環。為研究系統長時間歷程內的性態,通常做法是關注慢變過程——輪對橫向振動位移幅值隨速度增大過程中的變化情況,畫出Hopf分叉圖,見圖2。

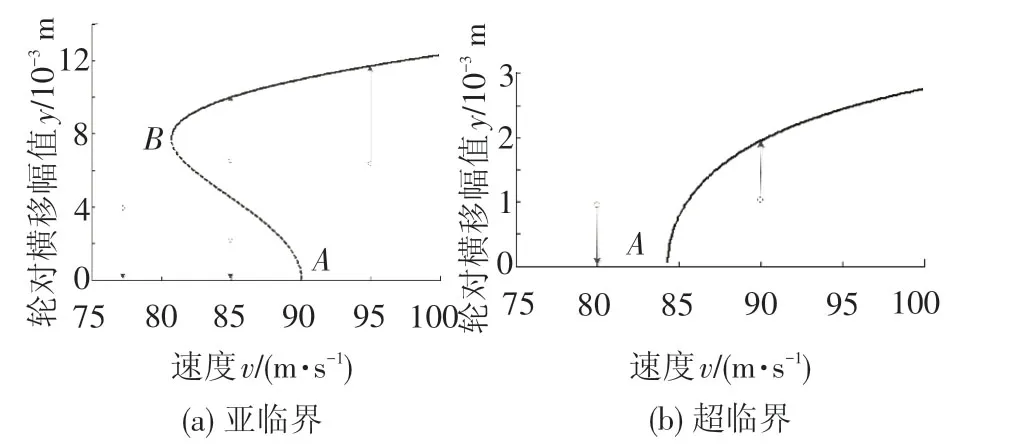
圖2 輪對系統Hopf分叉

輪對系統發生了亞臨界Hopf分叉見圖2(a),系統既出現了Hopf分叉(Hopf分叉點A)也出現了鞍結分岔(鞍結分岔點B)。Hopf分叉點A對應的速度90.1 m/s為線性臨界速度,鞍結分岔點B對應的速度80.7 m/s為非線性臨界速度。當速度小于非線性臨界速度時,輪對對任何擾動均具有抗干擾作用,其穩態運動都能收斂于平衡位置從而保持穩定;當速度位于非線性臨界速度和線性臨界速度之間時,當輪對的初始擾動幅值較小(虛線以下)時,輪對系統穩態運動逐漸收斂于平衡位置而保持穩定,但當出現大幅初始擾動(虛線以上)時則逐漸趨于實線從而失穩,此時系統小激擾穩定而大激擾失穩;當速度高于線性臨界速度時,系統完全失穩,任何擾動都能導致穩態運動發散。

輪對超臨界Hopf分叉見圖2(b),Hopf分叉點A對應的速度為84.3 m/s,為臨界速度。當速度低于84.3 m/s時,輪對系統穩定,對任何擾動均具有抗干擾效應,穩態運動均收斂于平衡位置;當速度高于84.3 m/s時,輪對系統失穩,任何擾動都能導致穩態運動發散直至出現極限環。

2.2 輪對系統的隨機穩定性

隨機穩定性分析可采用奇異邊界方法[19],這種方法的缺點是只適用于一維,對于高維問題則無能為力,但隨機平均法的降維功能恰好彌補了這一缺陷,為奇異邊界方法的實施奠定了基礎。

對于式(11)的一維能量擴散解過程H(t),其概率為1漸近穩定性與其平穩概率密度的存在性反映系統長期行為的性態,而系統長期性態可通過邊界性態間接獲取。接下來將重點分析能量擴散過程H(t)在左右2個邊界上的性態。

對于右邊界H=∞,有|m(∞)|=∞,根據一維擴散過程邊界分類[20]可知,右邊界邊界類型為無窮遠處第二類奇異邊界。對式(14)關于θ求期望,得

當H→∞時,R的低次項可忽略,H應對應R的高次項,則有,代入式(12)可得

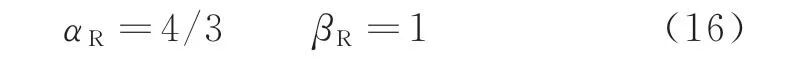
對于左邊界H=0,當H=0時,有σ2(0)=0,m(0)=0,則左邊界類型屬于第一類奇異邊界(套點)。此時對應的漂移和擴散系數滿足如下條件

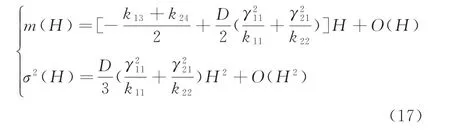
根據第一類奇異邊界理論[20],邊界擴散指數αL、漂移指數βL以及特征標值cL分別為(下標L表示左邊界)

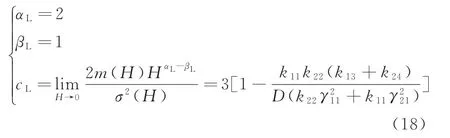
當特征標值cL＜1時,則有左邊界H=0是吸引自然邊界,由于右邊界不受特征標值影響,這樣解曲線H(t)會由于排斥效應遠離左邊界而逐漸趨向于左邊界,說明能量逐漸穩態收斂于0,此時系統解曲線H(t)是全局穩定的。

相反,當特征標值cL＞1時,左邊界也是排斥自然邊界,由于排斥效應解曲線H(t)會同時遠離左右邊界,解曲線H(t)最終會收斂于某個穩態能量處(見圖3)。此時系統解曲線H(t)是隨機不穩定的。

圖3 輪對隨機系統穩定性邊界分類示意

穩態能量的具體位置對應能量穩態概率密度函數的峰值,而能量穩態概率密度函數需要通過求解系統的FPK(Fokker Planck Kolmogorov equation)方程獲得,這項內容涉及隨機P 分叉的研究內容,本文暫不作討論,后續研究中會有涉及。

當cL=1時,左邊界為嚴格自然,此時邊界狀態處于吸引和排斥臨界狀態,對應系統隨機穩定性臨界狀態,可導出系統的隨機穩定域邊界。由式(18)可得

將表1中相關參數代入方程(19),可得兩類輪對系統的左邊界特征標值cL與激擾強度D、速度v的關系(見圖4),2種情形下規律基本一致,特征標值cL與速度v、激擾強度D正相關,速度v和激擾強度D越大,cL越大。當速度v和激擾強度D逐漸增大使特征標值大于1時,系統跨越絕對穩定區域邊界,出現概率意義失穩。

車輛穩定性研究的首要任務是將車輛運行速度控制在穩定安全域內,接下來將分別針對兩類輪對系統,確定隨機穩定域及穩定區域邊界,為車輛安全性設計提供理論指導。

兩類輪對系統的隨機穩定性臨界曲線見圖5,臨界曲線正好是絕對穩定區域與隨機不穩定區域的分界線,曲線上方為隨機不穩定域,曲線下方為絕對穩定域。車輛運行速度須控制在絕對穩定區域內,若速度跨越穩定域邊界,輪對發生隨機分叉,可能出現失穩,造成安全隱患。在穩定性分析時需要根據車輛參數確定系統穩定域,隨機激擾的激擾強度D可以通過試驗模擬,只要確定了最大可能的激擾強度Dmax,然后將車速控制在Dmax對應的絕對穩定區域內即可保證車輛的安全性。

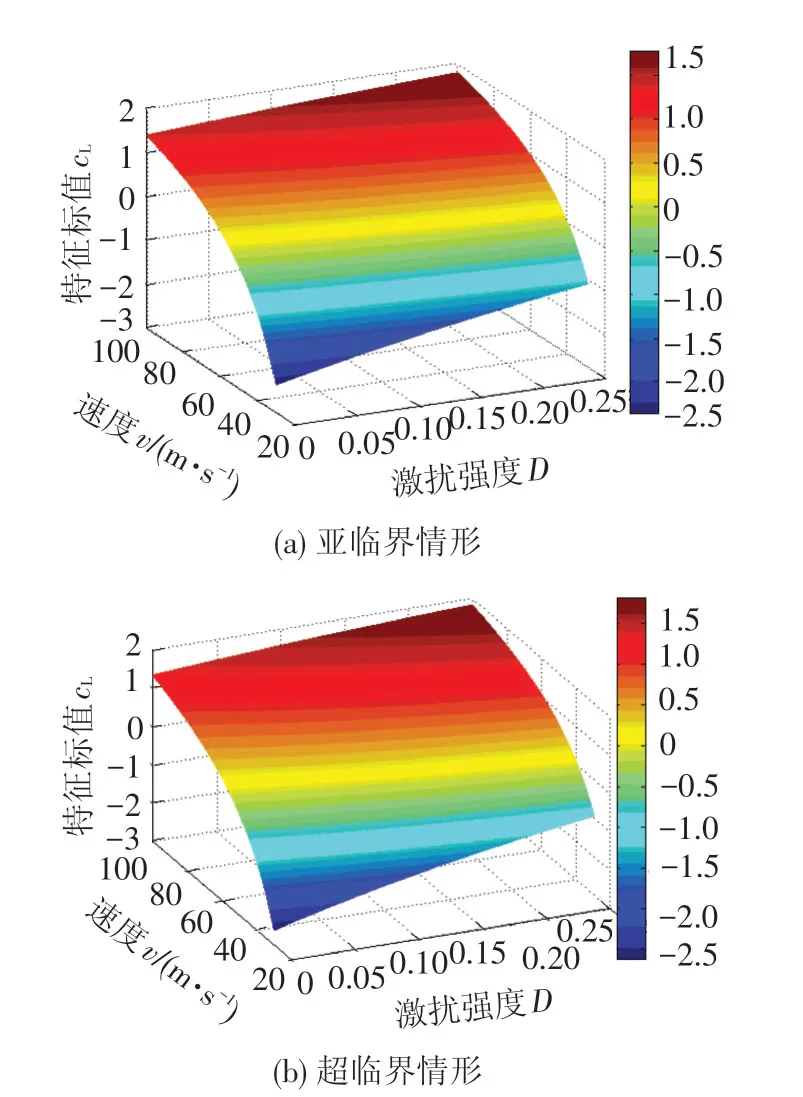
圖4 輪對隨機系統左邊界特征標值

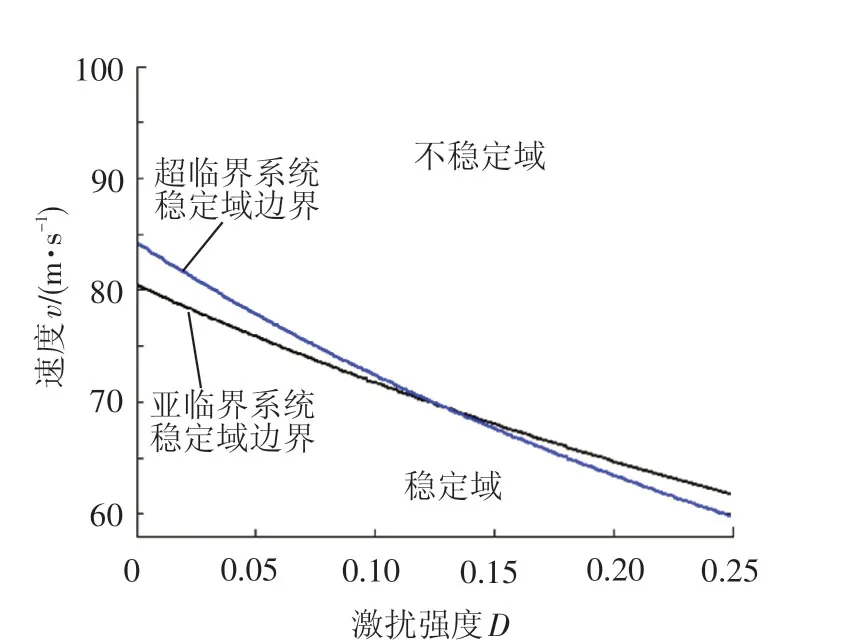
圖5 輪對系統隨機穩定臨界曲線

2.3 輪對系統的隨機分叉

隨機分叉與一般的確定性分叉不同,隨機分叉研究的重點主要集中于隨機激擾引起的非線性突變或躍遷現象。一般來說,隨機分叉主要有兩類:一類是隨機動態分叉(Dynamical bifurcation),又叫D 分叉;另一類是隨機維象分叉(Phenomenological bifurcation),也叫P 分叉。一般來說,動態分叉先于維象分叉,為了求解全局隨機臨界速度,本文只研究前者。

隨機動態分叉主要關注系統不變測度的動態特性,比較普遍的做法是通過研究Lyapunov指數這一不變測度的動態突變或躍遷變化,實現輪對的隨機動態分叉分析。因此,研究動態分叉的關鍵在于最大Lyapunov指數的計算。

實際上,由于隨機平均法保留原輪對系統的主要非線性特性,因此隨機平均后的平均It?隨機微分方程的最大Lyapunov指數可近似等價于原系統方程,則問題轉化為研究平均It?隨機微分方程(11)的最大Lyapunov指數。將平均It? 隨機微分方程(11)在H=0處線性化,得

由上式可求解得

則系統的最大Lyapunov指數為

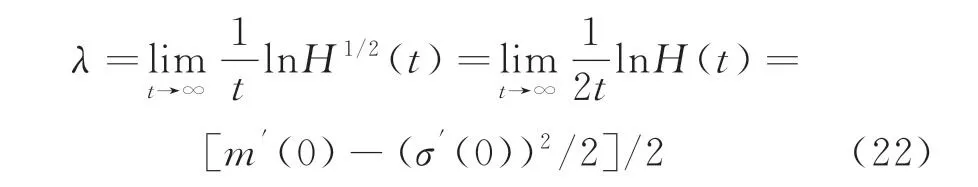
當H→0時,式(14)中關于R的高次項可忽略不計,對該式R的低次項部分關于θ求期望,可得

即R2=2H,則有

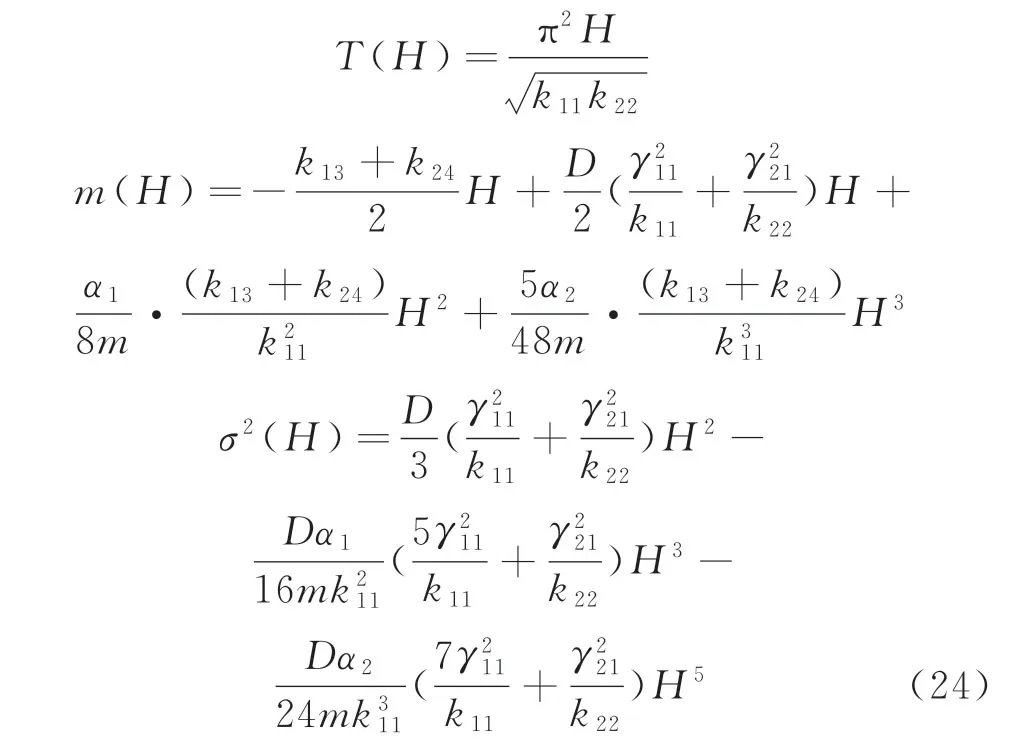
則可得輪對系統最大Lyapunov指數為

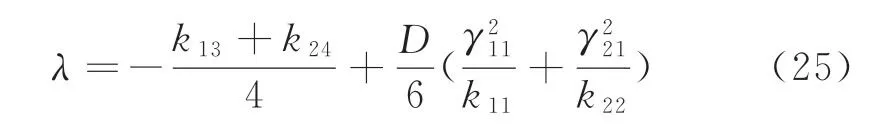
當λ＜0,輪對系統概率1漸近穩定,此時系統的能量增長速率慢于能量消耗速率,系統的總能量會逐漸耗散并趨于0,系統絕對穩定。最大Lyapunov指數λ的大小對應系統總能量的耗散速度,λ越小說明能量減小的越快,系統穩定性能越好。

當λ＞0,輪對系統為概率1 漸近不穩定,此時系統的能量消耗速率小于能量增長,總能量將逐漸累積,系統動能會逐漸增加,可能出現失穩及分叉現象甚至發生脫軌。

當λ=0,輪對系統處于隨機穩定臨界狀態,λ對應的零點為系統隨機動態分叉點。

輪對隨機系統的最大Lyapunov指數λ這一特性有點類似于確定系統中的特征根實部,λ＜0是系統概率1漸近穩定的充要條件。根據表1中的輪對參數,分別畫出了不同激擾強度D下兩類輪對系統的最大Lyapunov指數隨速度變化圖,見圖6。

由圖6可知,最大Lyapunov指數λ與激擾強度D、運行速度v具有正效應,當激擾強度D和運行速度v增大時,最大Lyapunov指數會逐漸增大并由負變正,此時輪對系統由概率為1穩定變為不穩定,系統發生隨機動態分叉。

圖6 最大Lyapounov指數隨速度變化

當λ=0時,為隨機動態分叉臨界點,此時對應的速度為動態分叉臨界速度,記為vD。

此外,分別針對兩類輪對系統,對比分析奇異邊界法與最大Lyapounov指數法的分析結果,兩類輪對系統對比分析見圖7(圖中激擾強度D=0.05),對比結果顯示2種方法的分析結果完美契合,動態分叉臨界速度vD與隨機穩定域邊界對應的速度值正好相同,且兩類輪對系統結論一致,側面應證了奇異邊界法和最大Lyapunov指數法的有效性。

綜上所述,隨機參激對輪對系統臨界速度影響較大,當隨機激擾強度逐漸增大時,臨界速度顯著減小。隨機動態分叉前輪對系統動態特征為概率1意義下的隨機穩定運動,此時系統絕對穩定;隨機動態分叉后系統動態行為比較復雜,其具體特征需要通過P分叉進一步研究。

2.4 隨機動態分叉與Hopf分叉的對比

前文通過隨機動態分叉研究得到了隨機動態分叉臨界速度vD,但是隨機動態分叉概念不夠直觀,為了詳細說明隨機動態分叉以便于理解,接下來將隨機動態分叉與確定性Hopf分叉進行對比,探究隨機動態分叉和傳統分叉之間的聯系,建立隨機動態分叉和傳統Hopf分叉溝通的橋梁。

圖7 隨機穩定性與動態分叉對比

隨機動態分叉臨界速度隨激擾強度的變化曲線見圖8。圖8中vDs和vDp分別為超臨界系統和亞臨界隨機動態分叉臨界速度,vH為超臨界系統Hopf分叉臨界速度,vA為亞臨界輪對系統鞍結分叉臨界速度。從圖8可以看出,當D→0時,超臨界輪對系統中動態分叉點逐漸趨近于Hopf分叉點,而亞臨界輪對系統中動態分叉點逐漸趨近于鞍結分叉點。當激擾強度時,隨機動態分叉逐漸退化為確定性分叉。需要說明的是超臨界輪對系統Hopf分叉點和亞臨界輪對系統鞍結分叉點都是各自輪對系統的全局(最小)臨界速度,當速度小于全局臨界速度時,系統絕對穩定,也就是說隨機動態分叉臨界速度可定義為輪對系統的全局隨機臨界速度。在隨機激擾下,臨界速度出現向前漂移現象,且隨著激擾強度增大,動態分叉臨界速度顯著變小。

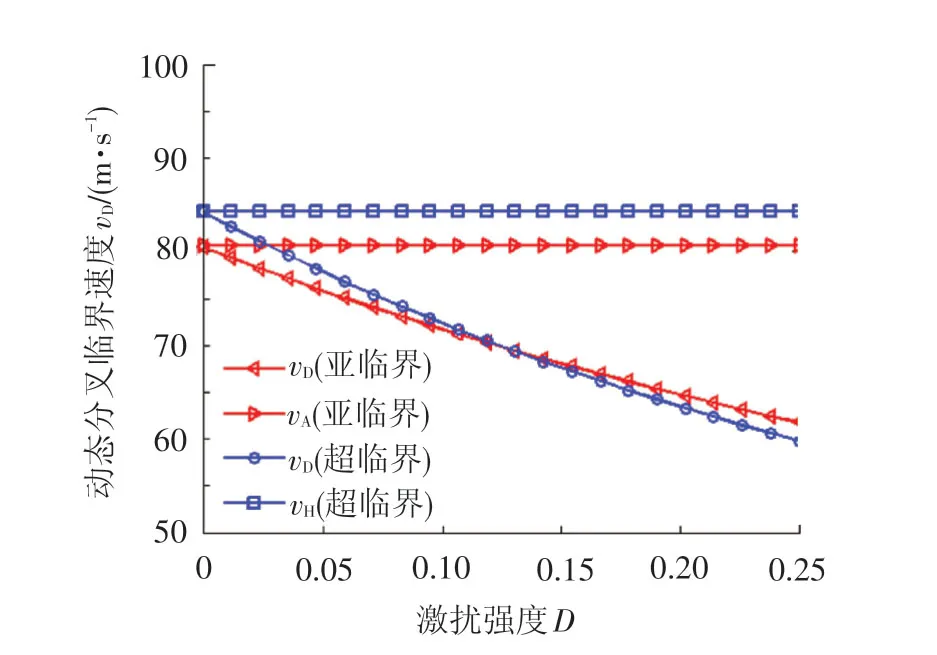
圖8 隨機動態分叉臨界速度隨激擾強度變化曲線

在傳統車輛穩定性理論中,認為車輛臨界速度跟外部激擾無關,激擾只是改變了系統的初始狀態,一旦激擾撤去,系統穩態解仍會呈現Hopf分叉相應特征。這一觀點本身并沒有問題,只是考慮問題的角度不同而已,實際上外部激擾存在時,車輛系統不能再單純考慮車輛本身,應該將它們作為一個耦合的大系統來分析。這也打破了確定性車輛系統中的臨界速度的思維定勢,車輛的臨界速度不再是單一的固定值,而是隨激擾強度變化而改變的,這也可以從理論上解釋車輛在不同線路下的失穩臨界速度不同的原因。

車輛在實際運行中隨機激擾無處不在,常規情況下車輛受到的隨機激擾源主要是軌道不平順激擾,但相對來說軌道不平順激擾屬于弱隨機因素,一般情況下其激擾強度D較小,根據前述理論分析結果可知,系統的臨界速度漂移量較小,符合實際車輛運行情況。但是當遇到大風、強震等極端激擾條件下,此時激擾強度D較大,車輛系統的臨界速度會顯著降低,穩定性能急劇惡化,而用Hopf分叉理論顯然無法解釋這一點。因此,常規運行時分析車輛穩定性時,隨機激擾影響不大,但遇到大風等強激擾環境時,隨機激擾的影響將不可忽視。

此外,隨機動態分叉點對應的速度為系統的全局隨機臨界速度,最大Lyapunov指數法對隨機激擾具有魯棒性,這為新的線路失穩判定方法提供了理論依據。最大Lyapunov指數可以通過時間響應序列直接計算,憑借這一優勢,該方法將可以直接應用到線路失穩判定中。

3 結論

本文運用隨機平均法研究了兩類輪對系統的隨機穩定性以及隨機動態分叉,定義了全局隨機臨界速度,提出了以最大Lyapunov指數法為基礎的失穩判定方法,獲得了以下主要結論:

(1)隨機動態分叉點對應的速度為輪對系統的全局隨機臨界速度,超臨界Hopf分叉系統中動態分叉點對應于Hopf分叉點,亞臨界Hopf分叉系統中動態分叉點對應于鞍結分叉點。

(2)動態分叉前輪對系統動態特征為概率1 意義下的穩定運動,分叉后輪對系統具體特征需要通過P分叉進一步研究。

(3)隨機因素對輪對系統平衡點的穩定性有決定性影響,隨機激擾使輪對系統的臨界速度出現向前漂移,隨著激擾強度增大,臨界速度漂移量顯著增大。

(4)輪對系統的臨界速度不再是單一的固定值,而是隨激擾強度變化而改變的,這也從理論上解釋了不同線路條件下失穩臨界速度不相同的原因。

(5)常規運行時分析車輛穩定性時,隨機激擾影響不大,但遇到大風等強激擾環境時,隨機激擾的影響將不可忽視。

(6)最大Lyapunov指數法可作為線路失穩判定的新方法。