水平結構競爭-互利群落優化算法*

黃光球，陸秋琴

西安建筑科技大學 管理學院，西安 710055

1 引言

工程中經常遇到十分復雜的優化問題，此類優化問題既存在大量局部最優解，其所包含的函數表達式又常常不可導，有時甚至連具體的函數表達式都無法知道。為了求解這些優化問題的全局最優解，目前所采用的方法是啟發式方法，群體智能優化算法就是其中的一種，這類優化算法對優化問題的函數表達式沒有特殊限制，因而具有較廣泛的適用性[1]。常用的群智能優化算法有：遺傳算法[2-3]、蟻群算法[4-5]、粒子群算法[6-7]、人工魚群算法[8]、生物地理學算法[9]、人工免疫算法[10]、蜂群算法[11]等。這類算法是依據一些簡單的自然現象而構造出來的，而且這些自然現象難以采用合適的數學模型加以描述。

為了克服傳統群智能優化算法存在的缺陷，本文選擇一種特殊的自然現象，即水平結構下的生物群落競爭-互利進化現象[12-13]，構造出了一種新的群智能優化算法，即水平結構競爭-互利群落優化算法（horizontal structure competition-mutually beneficial community optimization，HS-CBCO）。由于水平結構競爭-互利群落進化系統可采用種群動力學數學模型進行恰當描述，從而使HS-CBCO 算法奠定在堅實的數學理論基礎之上。

在自然界，任何種群都有確定的生態區域，它們在該區域中生存和繁衍。事實上，每一種群都占有自己的生態位[12]，生態位的鑲嵌是現實生物群落中的典型現象[13]。種群不但在同一生境中共存，而且是在消費相同的資源條件下共存。資源的局限性，使利用同一種群的資源相互制約。這樣，生態位的鑲嵌自然導致競爭關系，生態位決定著種群在競爭的群落結構中的地位和作用，而不存在生態位的鑲嵌的種群又會形成互利關系。水平結構競爭-互利群落進化指的是水平結構下生態位存在鑲嵌的群落系統中的生物種群相互競爭、互利，共同進化的現象。目前，有關水平結構競爭-互利群落進化系統理論研究已取得如下進展：

（1）群落水平結構特征分析[14-15]。研究群落的水平結構特征，以便對群落規模、營養供給水平和種群競爭和互利特征進行有效控制。

（2）營養水平對群落規模和群落結構的影響[16-17]。研究群落的營養供給水平對群落規模和群落結構的影響，發現其中的種群競爭和互利規律，為合理確定營養供給水平提供科學依據。

（3）群落結構特征對種群變化特征的影響[18]。揭示在種群競爭和互利環境下的群落結構特征對種群變化特征的制約規律，為有效控制種群變化特征提供科學依據。

上述有關水平結構競爭-互利群落進化理論的研究為本文算法的進一步研究提供良好的支撐。本文著重解決如下問題：

（1）如何將水平結構競爭-互利群落動力學模型轉化為能求解復雜優化問題的群智能優化算法。

（2）如何使得HS-CBCO 算法中的算子能充分反映不同種群內個體之間的相互作用關系，以便體現水平結構競爭-互利群落動力學理論的基本思想。

（3）如何證明HS-CBCO 算法的全局收斂性。

（4）如何確定HS-CBCO 算法的最佳參數設置。

（5）如何進行HS-CBCO 算法的求精和探索能力及其協調性分析。

2 HS-CBCO 算法設計

考慮優化問題：

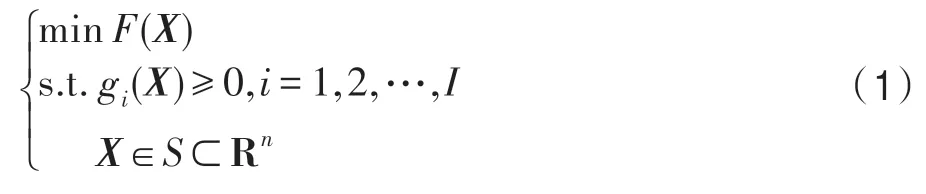
式中，Rn是n維歐氏空間；X=(x1,x2,…,xn)是一個n維決策向量；S為搜索空間；f(X) 為目標函數；gi(X)≥0 為第i個約束條件，i=1,2,…,I，I為不等式約束條件個數。目標函數f(X)和約束條件gi(X)不需要特殊的限制條件。

2.1 算法場景設計

在生態系統中，水平結構是指多個不同類別的生物種群所消費的資源為同一類型。在同一水平結構內的種群間相互作用主要是競爭和互利。假設一個生態系統中有K個種群在其中活動，其編號分別為1,2,…,K，記為P={1,2,…,K}。

時期t，種群k內有Nk(t)個生物個體（簡稱個體），這些個體的編號的集合記為，因此該生態系統中的個體總數為N(t)=M(K,t)，。若按種群編號順序對所有種群中的個體進行統一編號，則種群k內的Nk(t)個個體的編號為Pk={1+M(k-1,t),2+M(k-1,t),…,Nk(t)+M(k-1,t)}。已知個體的編號為m，當m滿足M(u-1,t)＜m≤M(u,t)時，該個體所在的種群編號NL(m)=u。

在一個生態系統中，每一種群都占有自己的生態位，生態位是指種群對多種資源的利用范圍。當種群的生態位出現鑲嵌（又稱重疊）時，種群之間會產生競爭關系。生態系統中已發現有5 種競爭格局，即正態分布型（C1）、離散分布型（C2）、最鄰近型（C3）、均勻型（C4）、單調遞減型（C5），記為C={C1,C2,C3,C4,C5}。

在該生態系統中，不存在生態位鑲嵌的種群之間可能存在互利關系，但該互利關系不是一成不變，而是隨時間變化的。若一個種群與另外一個種群存在競爭關系，則它們之間就不存在互利關系，反之亦然。

在一個種群的內部，各生物個體之間存在相互影響關系，這種相互影響關系分為兩種類型，即普通影響關系和強烈影響關系。所謂普通影響關系是指某個體受到其他普通個體的影響，而強烈影響關系是指某個體受到其他強壯個體的深刻影響。

種群中的生物個體在進化期間，其特征既會受到種群之間的競爭和互利影響，又會受到同一種群內其他生物個體的影響，且這種影響是隨時間變化的。

下面將上述現象與優化問題（1）的全局最優解的求解過程對應起來，即有：生態系統與優化問題（1）的搜索空間S相對應，時期t，該生態系統中的一個生物個體對應于一個優化問題（1）的一個試探解，種群k所包含的Nk(t)個生物個體所對應的優化問題（1）的試探解集為，其中，m=1,2,…,Nk(t) ；種群k中的一個個體的特征j對應于優化問題（1）試探解中的一個變量；種群k中所有個體的特征數與試探解的變量數相同，都為n，令個體特征的編號集合Z={1,2,…,n}。個體適應度指數即IPI 指數（individual physique index）對應于優化問題的目標函數值。試探解質量越好，其對應的IPI指數越高，反之亦然。時期t，對于優化問題（1），個體的IPI 指數計算方法為：

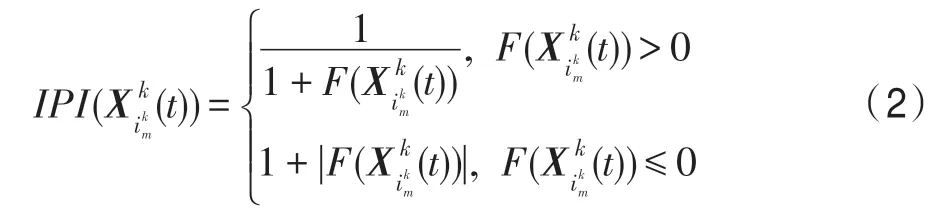
2.2 水平結構競爭-互利群落動力學模型

假設種群所消費的資源以某種特性參數向量z表示，具有特征z的資源消耗數量由函數k(z)來確定。函數k(z)中z值的集合稱為資源譜。假設一種群資源消費以某種概率分布來描述其特性，其密度函數f(z)稱為資源利用函數，具有均值z0和有限方差σ2。這時，種群的生態位取決于資源譜上的點z0和給定的點z0附近隨機分布的密度函數f(z)。當一個群落由若干為共同的食物資源而進行競爭的種群構成時，自然認為適合于不同種群的z0點彼此之間有一定距離。這種情況下，種群生態位鑲嵌所造成的競爭現象必然會在資源空間里相應的資源利用函數fi(z)產生定義域相交的現象。最簡單的例子如圖1所示，圖中fi(z)為形狀相同的正態分布密度曲線，沿著資源譜均值之間以距離d分離；k(z)=const，如果對所有曲線，w為均方差，那么比值w/d可視為生態位接近的度量，或者說是群落種間隔離度度量；按照穩定性條件，比值w/d可以用于判斷生態位鑲嵌的界限[12-13]。

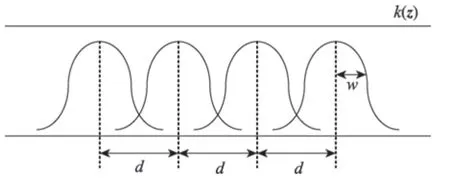
Fig.1 Niche mosaic of 1-D resource spectrum圖1 1 維資源譜的生態位鑲嵌

兩個種群在資源譜上利用資源的分離程度稱為生態位分離。d表示平均分離度，w稱為變異度，生態位分離度為d/w。當生態位充分分離時，d/w大；當生態位重疊時，d/w小。

為簡單起見，以后總假定資源譜的維數為1 維，即z為1 維，因此可將z的黑體去掉而表示為z。K個種群競爭-互利群落的動力學模型為：

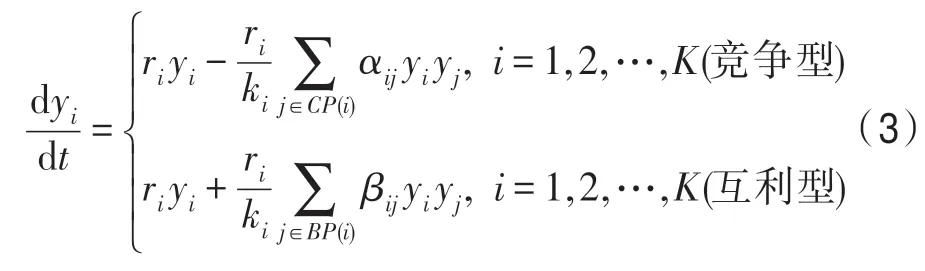
式中，yi為種群i的規模；CP(i)為與種群i競爭的其他種群集合；BP(i)為與種群互利的其他種群集合；ri為種群i的內稟增長率；ki為種群i的生態位容量，ki=∫k(z)fi(z)dz；βij為種群i與種群j之間的互利系數；αij為種群i與種群j之間的競爭系數，由下式計算：

為方便起見，令A=[αij]K×K，A稱為競爭矩陣。當A取不同的形式時，表示不同的競爭格局。常見的競爭矩陣A有如下5 種形式：

（1）正態分布型。對于每一個種群i，有：

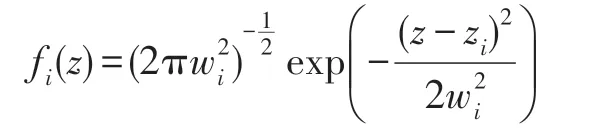
式中，zi為生態位的中心點，為正態分布的方差。如果種群i和種群j生態位的中心點彼此相距dij，那么由式（4）可計算得：

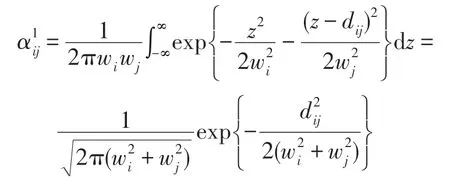
如果所有fi(z)都有相同的方差，且順序號碼相鄰就意味著生態位相鄰，則dij=|i-j|d，且：

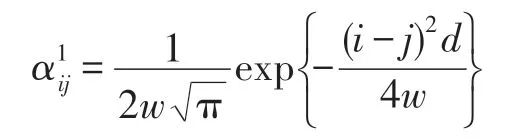
當規定競爭系數的自鑲嵌程度為1 時，便有：

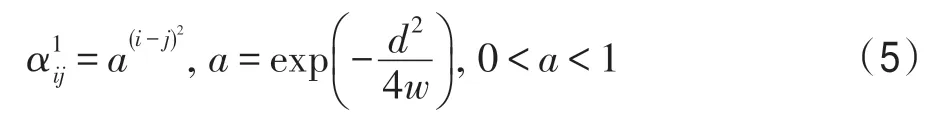
（2）離散分布型。將K個種群進行編號，使它們在資源空間彼此距離的大小可用下標差的絕對值|i-j|來度量。不難認為，競爭現象是隨種群生態位間距加大而減弱的，于是競爭系數可表示成：

（3）最鄰近型。設K個種群中的每一種群僅和自己最鄰近的種群競爭，而不和其他種群競爭。這時如果用a表示兩個相鄰生態位鑲嵌的度量，那么競爭矩陣為：

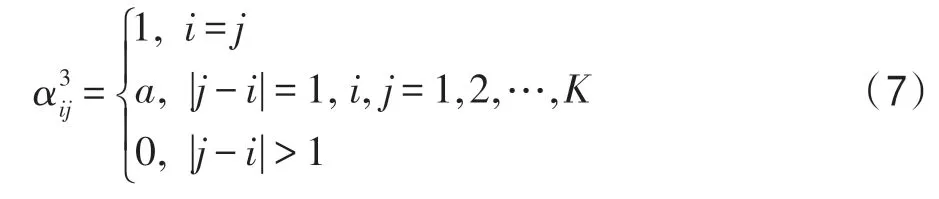
（4）均勻型。設K個種群中的每個種群均以相同的程度a與其他種群競爭，則：

（5）單調遞減型。設K個種群中的每個種群均以單調遞減的程度a與其他種群競爭，則：

為快速計算，需將式（3）改為離散遞推形式：

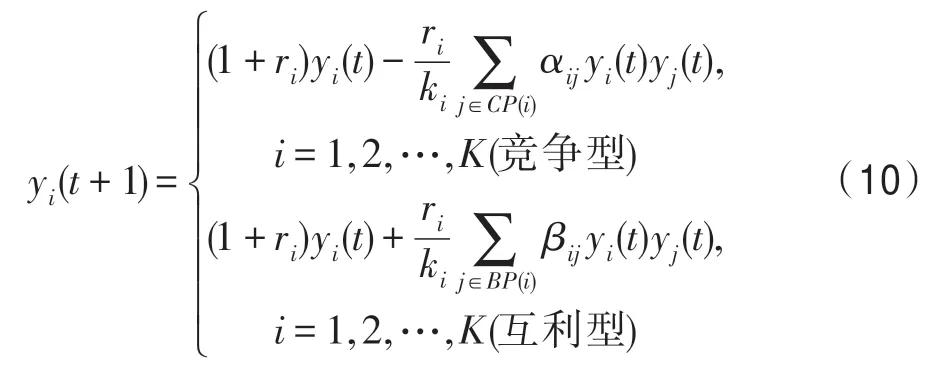
2.3 算子設計方法

HS-CBCO 算法是利用水平結構競爭-互利群落動力學理論構造種群演化算子，以實現生物個體間信息交換，進而實現對優化問題（1）的全局最優解的搜索。

2.3.1 競爭和互利種群集合確定方法

對于當前種群k，k∈P，其競爭型種群集合CP(k)是依據競爭格局類型c確定的，即對于c∈C，有：

（1）若c=C1或C2或C5，則從種群集合P中選擇3 個編號最相近的種群，由其編號形成集合CP(k)，但k?CP(k)；種群i與種群k編號相近意味著|k-i|盡可能小，但k≠i。

（2）若c=C3，則將K個種群按其編號構成一個閉環，即當k=1時，CP(k)={2,K}；當1 ＜k＜K時，CP(k)={k-1,k+1}；當k=K時，CP(k)={1,K-1}。

（3）若c=C4，則從K個種群中隨機選擇3 個種群，由其編號形成集合CP(k)，但k?CP(k)。

對于當前種群k，k∈P，其互利型種群集合BP(k)是從不參與競爭的種群集合P-CP(k)中隨機選擇3 個種群，這些種群與當前種群k形成互利關系集合BP(k)，但k?BP(k)。

2.3.2 特征生物個體集合確定方法

對于當前種群k，k∈P，當前個體i∈Pk，有：

（1）競爭型個體集合CI(k)。從當前種群k的競爭型種群集合CP(k)中的所有生物個體中，隨機選擇L個生物個體，由其編號形成競爭型個體集合CI(k)。L稱為施加影響的個體數。

（2）互利型個體集合BI(k)。從當前種群k的互利型種群集合BP(k)中隨機選擇L個生物個體，由其編號形成互利型個體集合BI(k)。

（3）普通影響型個體集合GI(k)。在當前種群k的所有個體集合Pk中，隨機選擇L個生物個體，由其編號形成普通影響型個體集合GI(k)。

（4）強烈影響型個體集合SI(k)。在當前種群k的所有個體集合Pk中，隨機選擇L個生物個體，這些個體的IPI 指數高于當前個體i，由其編號形成強烈影響型個體集合SI(k)。

（5）虛弱個體集合WI(k)。在當前種群k的所有個體集合Pk中，隨機選擇L個IPI 指數最低的生物個體，由其編號形成虛弱個體集合WI(k)。

2.3.3 算子設計方法

HS-CBCO 算法利用水平結構競爭-互利群落動力學理論及其控制下的種群演變規律構造種群演化算子，來實現個體間的信息交換，進而實現對優化問題全局最優解的搜索。HS-CBCO 算法的群演化算子如下所述。

（1）競爭算子。該算子依據競爭關系構造，對當前種群k來說，k∈P，當前個體i∈Pk，由式（10）得：

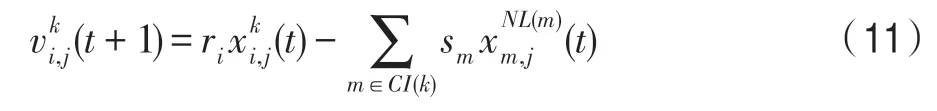
（2）互利算子。該算子依據互利關系構造，即對當前種群k來說，k∈P，當前個體i∈Pk，特征j∈Z，則由式（10）可得：

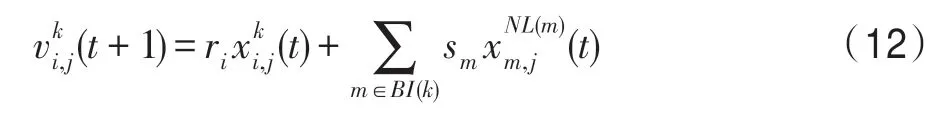
（3）普通影響算子。該算子依據普通影響關系構造，即對于當前種群k，k∈P，當前個體i∈Pk，特征j∈Z，有：

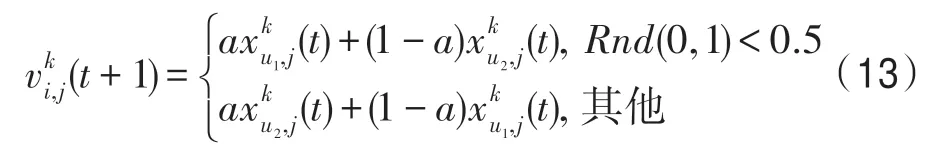
式中，u1、u2從GI(k)中隨機選擇，且滿足u1≠u2；a=Rnd(-0.5,0.5)。

（4）強烈影響算子。該算子依據強烈影響關系構造，即對于當前種群k，k∈P，當前個體i∈Pk，特征j∈Z，有：

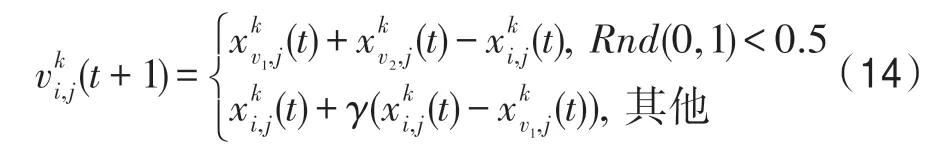
式中，v1、v2從SI(kU)中隨機選擇，且滿足v1≠v2；γ=Rnd(-1,1)。

（5）新生算子。該算子用于為某個種群新生m個新個體，即對于種群k，k∈P，待新生的個體編號集合為NGk(m)，有：

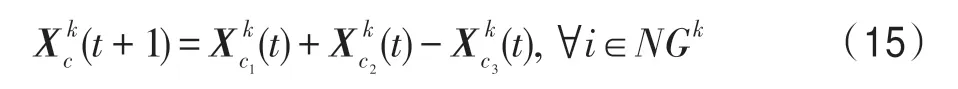
式中，新生個體的編號c∈NGk(m)；c1、c2、c3從集合SI(k)中隨機選擇。

（6）死亡算子。該算子用于為某個種群清除m個虛弱個體，即對于種群k，k∈P，從集合WI(k)中挑出m個體進行清除。

（7）選擇算子。通過各算子產生新一代生物個體之后，將新一代個體與相應的父代個體進行比較，較優者保存到下一代中。對于當前種群k，k∈P，當前個體i∈Pk，有：

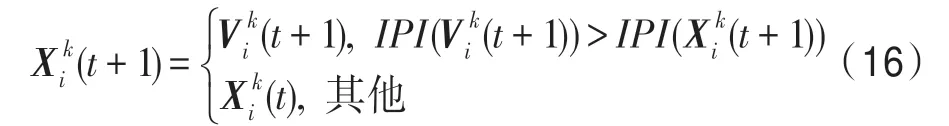
2.4 HS-CBCO 算法設計

（1）初始化：令時期t=0，按第4.1 節介紹的方法設置HS-CBCO 算法涉及到的所有參數：演化時期數G、全局最優解計算誤差ε、個體特征受影響的最大概率E0、施加影響的個體數L、種群數K；隨機選擇當前初始最優解X*。

（2）按第4.1 節介紹的方法設置水平結構競爭-互利群落動力學模型參數yi(0)，令Ni(0)=[yi(0)]，i=1,2,…,K；[y]表示對y取整；對各種群中的所有個體進行統一編號，生成個體集合，k=1,2,…,K。

（4）在競爭-互利格局集合C中為生態系統隨機指定一種競爭-互利格局c，依據c計算競爭矩陣A。

（5）執行下列操作：

（6）結束。

2.5 HS-CBCO 算法的特點

（1）Markov 特性。從HS-CBCO 算法各算子的定義式（11）～式（15）知，時期t+1任何一新試探解的生成只與該試探解在時期t的狀態有關，而與該試探解在時期t以前是如何演變到時期t的狀態的歷程無關，因而HS-CBCO 算法具有Markov 特性。

（2）“步步不差”特性。從生長算子的定義式（16）知，HS-CBCO 算法的每步演化都不會向比當前狀態更差的狀態轉移，因而HS-CBCO 算法的演化過程具有“步步不差”特性。

2.6 HS-CBCO 算法的時間復雜度

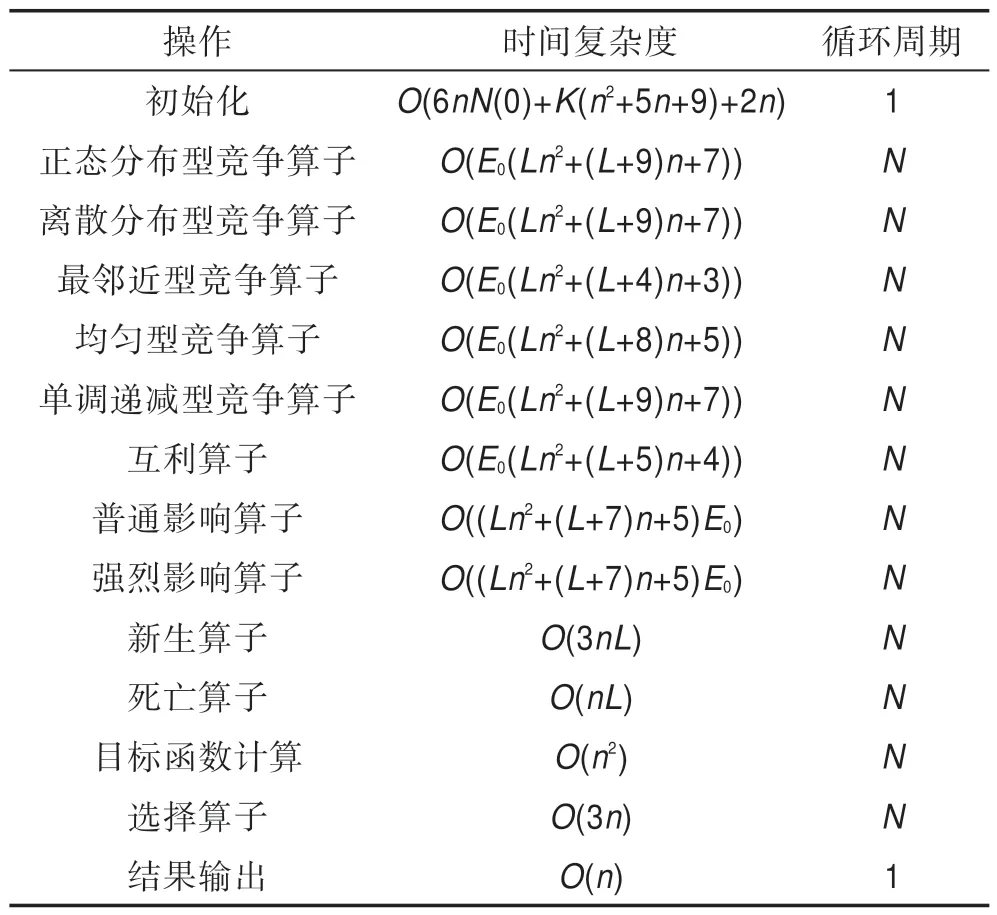
Table 1 Table of HS-CBCO time complexity表1 HS-CBCO 時間復雜度計算表

2.7 HS-CBCO 算法的優勢

定理1 若一個群智能優化算法所擁有的算子越多，且各算子被隨機獨立調度執行，則該算法的性能越優良。

證明 假設一個群智能優化算法有n個算子，當該算法求解優化問題X時，這n個算子求解優化問題X成功的概率分別為p1,p2,…,pn。因每個算子在求解優化問題X時均是被隨機獨立調度執行的，故該算法在其n個算子的聯合作用下求解優化問題X成功的概率q為：

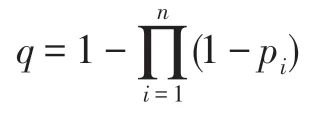
因0 ＜pi＜1，故0 ＜1-pi＜1，i=1～n；當n越大時，越小，而q則越大。此結論表明，若一個群智能優化算法的算子越多，則該算法求解一個優化問題時成功的概率越大。因此，算子越多，算法性能越優良。

HS-CBCO 算法擁有10 個算子，且每個算子均是被隨機調度執行的，故HS-CBCO 算法滿足定理1 的條件，因而HS-CBCO 算法具有優良的性能。 □

與已有的基于種群動力學的優化方法[19-20]相比，HS-CBCO 算法具有如下異同點：

（1）HS-CBCO 算法所依據的生物場景中詳細考慮了生物種群的水平營養結構特點，而現有的其他基于種群動力學的優化方法沒有考慮這一關鍵特征。

（2）HS-CBCO 算法將種群動力學中一些常規特征，如競爭、互利等特征，也包含到了算法中，該特點與基于種群動力學的優化方法類似。

（3）由于存在上述（1）和（2）的特點，HS-CBCO 算法比基于種群動力學的優化方法擁有更多的算子，故該算法特別適合應用于分布式多任務環境，如云計算環境。

3 HS-CBCO 算法的全局收斂性證明

在證明HS-CBCO 算法的全局收斂性之前，先介紹由Iisufescu 在文獻[21]提出的定理：

定理2 設P′是一N階可歸約隨機矩陣，也就是通過相同的行變換和列變換后可以得到P′=，其中C是M階本原隨機矩陣并且R≠0，T≠0，則有：

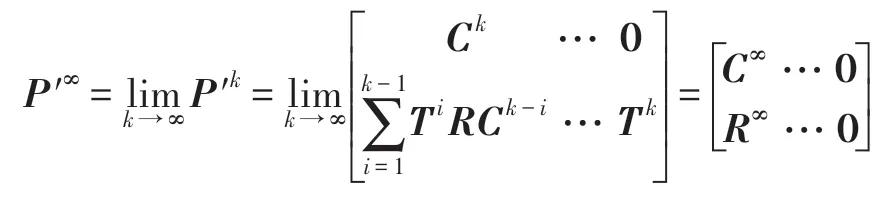
上述的矩陣是一個穩定的隨機矩陣且P′∞=1′P′∞，P′∞=P′0P′∞唯一確定并且與初始分布無關，P′∞滿足如下條件：

利用定理2，不難證明HS-CBCO 算法的全局收斂性。其證明過程如下所述。

由算法HS-CBCO 算法知，優化問題（1）的搜索空間等價于一個生態系統，該生態系統有K個種群；在時期t，種群k有Nk(t)個生物個體，k=1,2,…,K；將各種群中的所有生物個體重新排列成N(t)個生物個體，，形成新的生物個體序列為。每個生物個體（i=1,2,…,N(t)）即為優化問題（1）的一個試探解，其目標函數值為（按式（1）計算），則所有生物個體的狀態所形成的集合為：

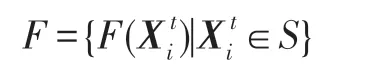
進一步令：

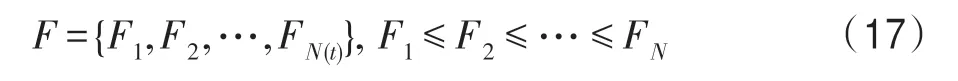
不失一般性，令F1即為所求的全局最優解。將式（17）的下標取出形成一個集合，即：

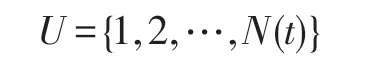
集合U中的元素就是隨機搜索時每個生物個體可能所處的狀態。假設在某時期搜索到的最好目標函數值為Fi，其對應的狀態為i。顯然，由式（17）知，下一時期搜索時，若向更優的狀態k轉移，則應滿足k＜i；相反，若向更差的狀態k轉移，則應滿足k＞i，如圖2 所示。

?Xt∈S有F1≤F(Xt)≤FN，將S劃分為非空子集為：

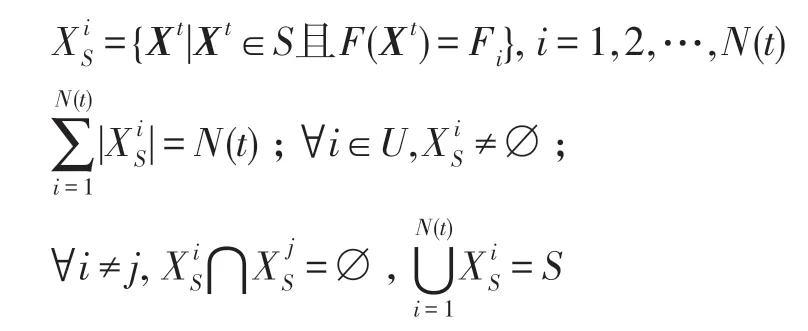
Fig.2 State transition in random search圖2 隨機搜索時狀態轉移圖

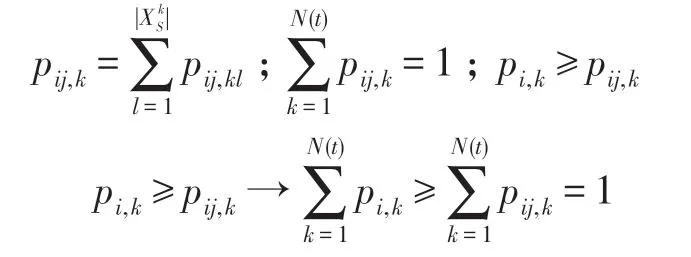
證明（1）對于式（19），設狀態i為時期t某生物個體Xt的狀態，該狀態i當然就是該生物個體至今已達到的最好狀態。在HS-CBCO 優化算法中，每次進行新的演化都總是對該生物個體當前狀態i進一步向更好狀態的更新，即有：

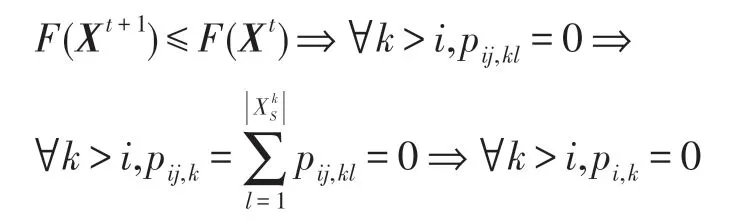
上式的含義是：若i為時期t某生物個體的狀態（也必是該個體已達到的最好狀態），在時期t+1 該生物個體的演化只會向更好的狀態更新，因此從i開始不可能轉移到比i差的任何其他狀態上去；由式（17）知，若要Fk＞Fi，則比狀態i差的狀態k必滿足k＞i，也即最好狀態要么保持原狀，要么只能向更好的狀態更新（即做到步步不差），如圖2 所示。

（2）對于式（20），設某生物個體的當前狀態為i，當然必是該生物個體迄今為止已達到的最好狀態，在時期t+1，該生物個體隨機選擇各種算子以期轉移到更好的狀態上，有競爭算子、互利算子、普通影響算子、強烈影響算子可供選擇：

①若i是全局最優狀態，即i=1，則下一步轉移必選k=1（因為不可能轉移到比當前狀態還差的狀態上去），即必以概率p1,1=1 轉移到該全局最優狀態上去。因p1,1=1 ＞0，命題得證。

②若i不是全局最優狀態，則在全局最優狀態1和當前狀態i之間必至少存在一中間狀態k（如圖2所示），使得F1≤Fk＜Fi，即1 ≤k＜i，此時當前狀態i可以轉移到狀態k上去（因為新狀態k比當前狀態i更優），也就是pi,k＞0，命題得證。

綜合上述情況，可得?k＜i,pi,k＞0。 □

定理3 HS-CBCO 算法具有全局收斂性。

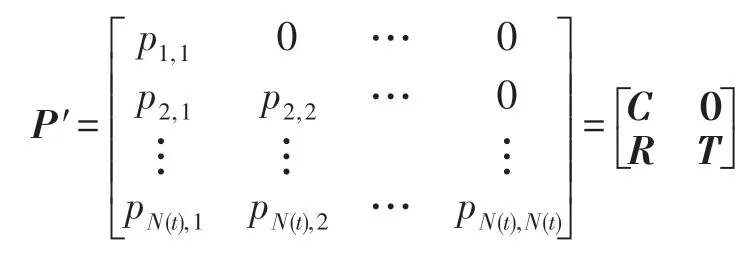
根據引理中式（20）結論得：

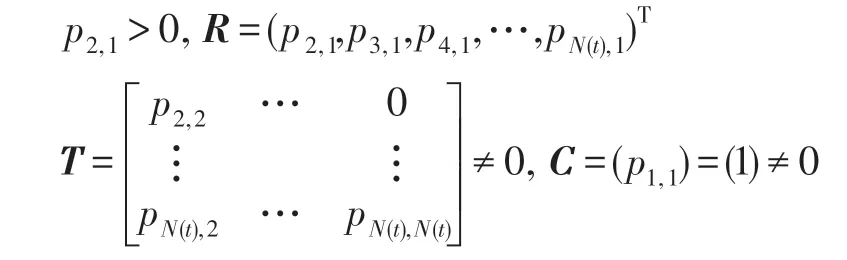
由以上可知轉移矩陣P′是N(t)階可歸約隨機矩陣，滿足定理2 的條件，因此下式成立：

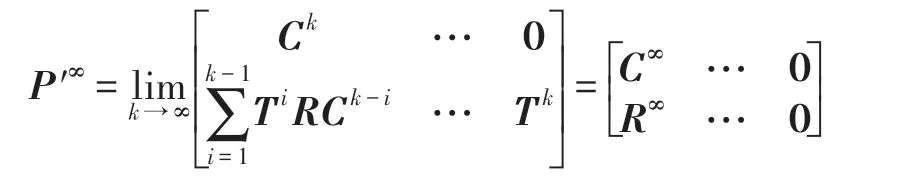
因C∞=C=(1)，T∞=0，故必有R∞=(1,1,…,1)T，這是因為由式（18）知轉移矩陣P′中每行的概率之和為1。因此有：

上式表明，當k→∞時，概率pi,1=1，i=1,2,…,N(t)，也即無論初始狀態如何，最后都能以概率1 收斂到全局最優狀態1 上。于是得：

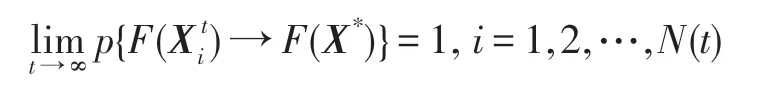
因此，HS-CBCO 優化算法具有全局收斂性。□

4 HS-CBCO 算法參數設置及其普適性

4.1 參數設置方法

HS-CBCO 算法參數包括兩部分：一部分是水平結構競爭-互利群落動力學模型參數，該部分參數為算法內置參數，無需用戶進行設置；另一部分是算法運行控制參數，此類參數需要用戶根據情況進行設置。

（1）水平結構競爭-互利群落動力學模型參數確定方法。該模型參數的選擇依據是確保yi(t)(i=1,2,…,K)具有較好的隨機性。依據文獻[12]介紹的參數取值方法并經隨機化后，可得ri=Rnd(0.3,0.4)，ki=Rnd(20,30)，yi(0)=Rnd(60,70)，i=1～K；a=0.5，βij=Rnd(0.17,0.24)，i,j=1～K。應用此取值策略，當K=10 時，任取第5 號種群進行測試，種群中的個體數y5變化情況如圖3 所示。從圖3 可知，y5具有很好的隨機性。

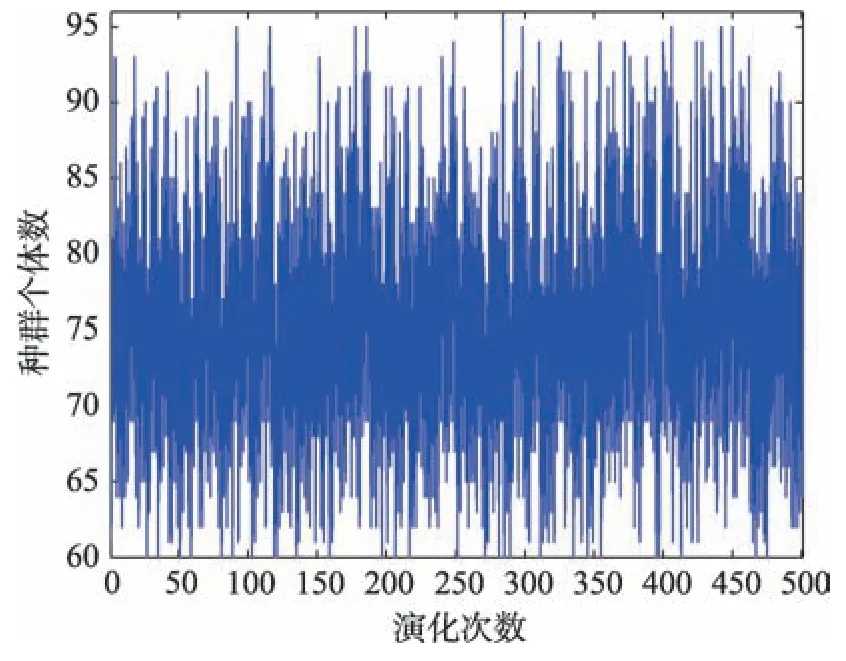
Fig.3 Randomicity of individual y5in population 5圖3 第5 號種群中個體y5的隨機性

（2）算法運行控制參數設置方法。HS-CBCO 算法的運行控制參數有：演化時期數G、全局最優解計算誤差ε、個體特征受影響的最大概率E0、施加影響的個體數L、種群數K。G和ε是兩個互補參數，只要滿足其中一個即可。ε由所求解的工程優化問題決定，通常可取ε=10-5～10-10即可，G由計算設備性能決定，G可取充分大，不妨設G=108～1010。HS-CBCO算法關鍵參數只有E0、L、K。因此，下面主要討論3 個關鍵參數E0、L、K的取值方法。由于Bump 優化問題極難求解，且與一些工程優化問題特征類似，故以Bump 優化問題為例來探明E0、L、K的取值方法。Bump 優化問題如下：

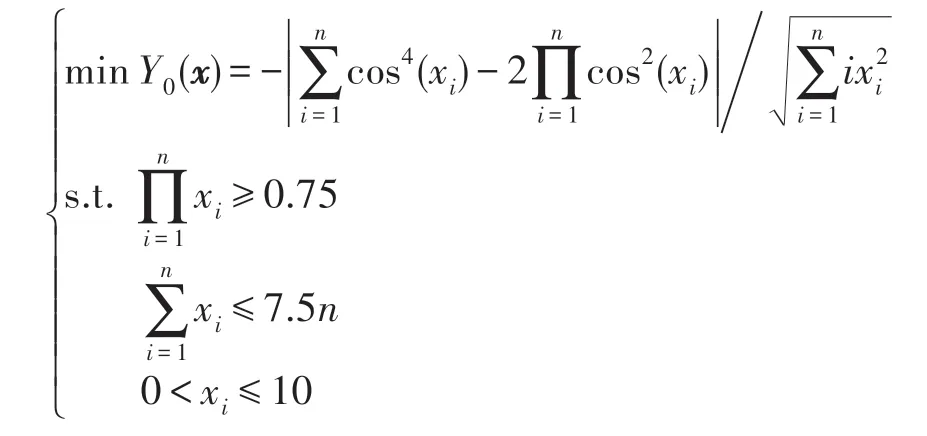
令Favg表示平均最優目標函數值，Tavg表示平均計算時間。當L取不同值時，采用HS-CBCO 算法求解Bump 優化問題，令n=50，E0=0.01，K=10，G=108，運行50 次，表2 描述了L與Favg和Tavg之間的關系。結果表明，當L=3～6 時，Favg的精度達到最高，而Tavg增加較低。由此可見，L=3～6 為L的最佳取值區間。

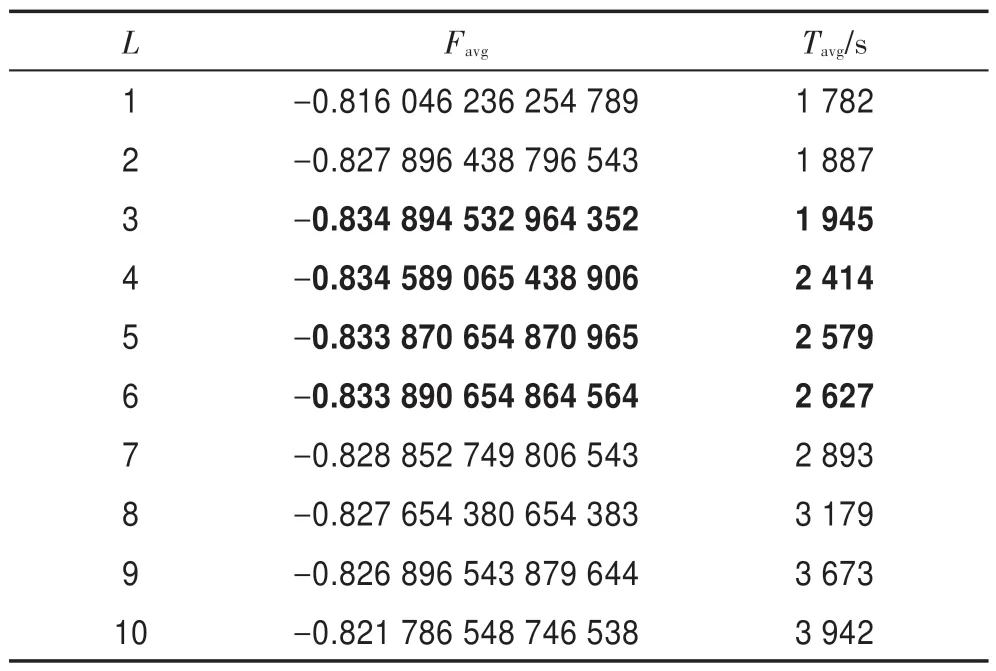
Table 2 Relation of L with Favgand Tavg表2 L 與Favg和Tavg之間的關系

令n=50，L=3，K=10，G=108，HS-CBCO 算法運行50 次。表3 描述了參數E0與Favg和Tavg之間的關系。結果表明，當E0=0.006～0.1 時，Favg的精度相對較高，且Tavg較少；當E0＞0.2 時，Tavg增加很大，且Favg精度也大大降低；特別是當E0=1 時，無法獲得最佳解。由此可見，E0=0.006～0.1 為E0的最佳取值區間。

令E0=0.01，L=3，G=108，HS-CBCO 算法運行50 次。表4 描述了K與Favg、Tavg之間的關系。從表4 可以看到：當K=8～16 時，Favg的精度相對較高，且Tavg較少；當K＞18 時，Tavg增加很大，且Favg精度也逐步降低。由此可見，K=8～16 為K的最佳取值區間。

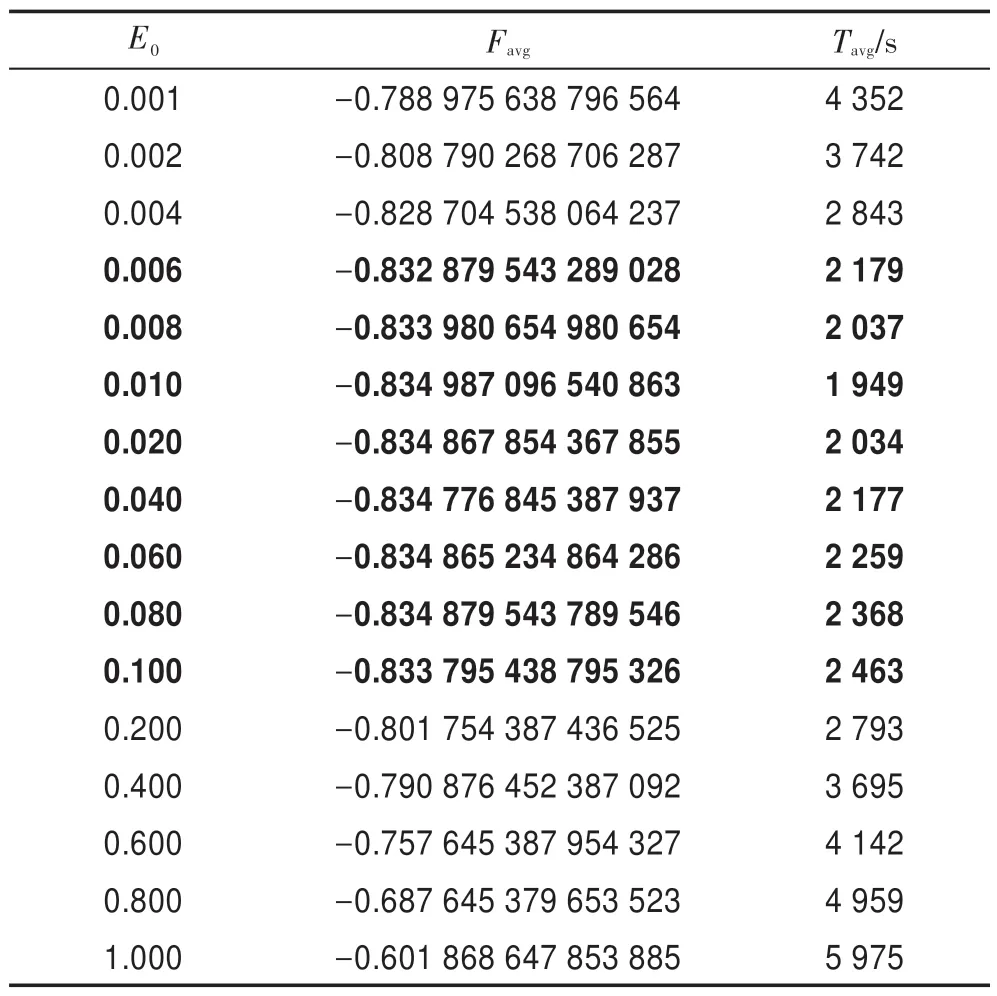
Table 3 Relation of E0with Favgand Tavg表3 參數E0與Favg和Tavg之間的關系

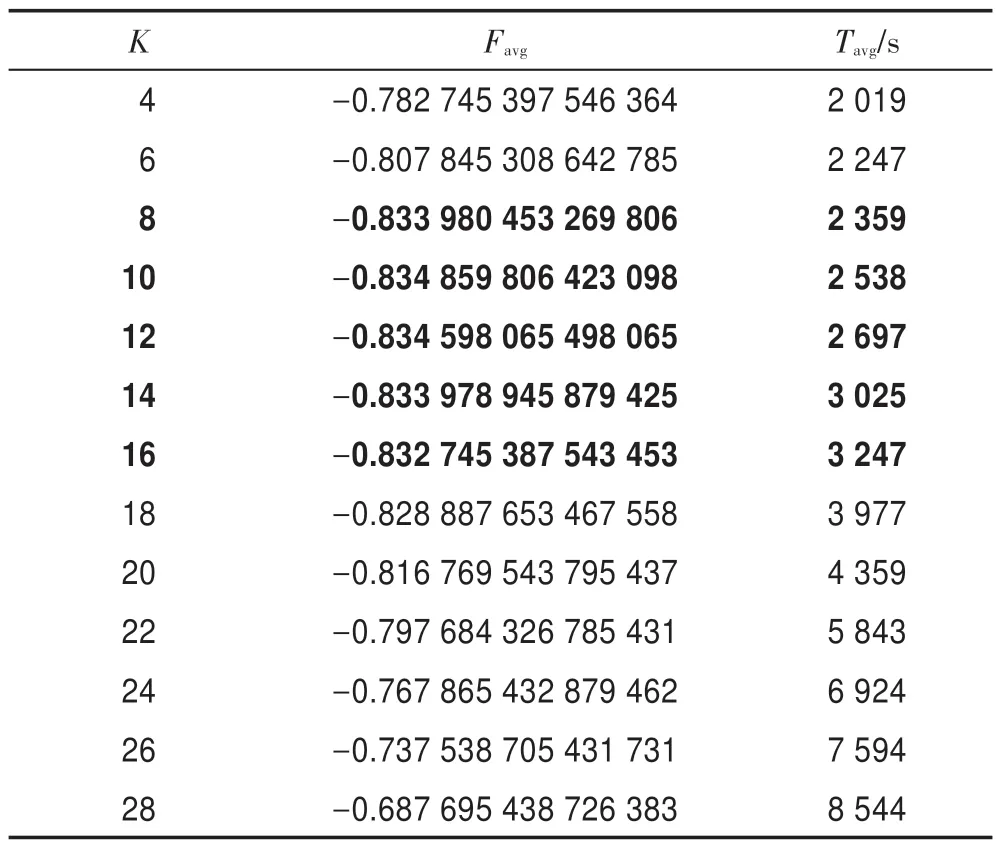
Table 4 Relation of K with Favgand Tavg表4 K 與Favg和Tavg之間的關系

4.2 參數設置的普適性分析

4.1 節確定了參數L、E0、K的最佳取值區間。由于Bump 優化問題與工程中存在的一類優化問題相似，因此從求解Bump 優化問題所獲得的參數設置，具有一定的普適性。事實上，參數L、E0、K的取值并不要求太精確，不精確的參數取值僅影響計算時間的長短，對求解精度的影響較小。優化問題的維數n對HS-CBCO 算法的求解時間有影響，參數L、E0、K的取值規律是，優化問題的維數n越高，L和K的取值應越大，E0的取值應越小。根據場景及需求進行參數調整的思路如下：

（1）若n≤100，則L=3，E0=0.01，K=8～10。

（2）若100 ＜n≤500，則L=4，E0=0.005，K=9～12。

（3）若500 ＜n≤1 000，則L=5，E0=0.000 1，K=11～14。

（4）若n＞1 000，則L=6，E0=0.000 05，K=13～16。

5 HS-CBCO 算法與其他算法的性能比較

CEC 2013[22]是一組新的群智能優化算法測試函數，該組測試函數包含有28 個經過精心設計的基準函數，這些基準函數是由一些傳統的著名測試函數（如Sphere 函數、Schwefel 函數、Rastrigrin 函數、Ackley 函數、Griewangk 函數、Rosenbrock 函數等）經改造而得，改造方法包括復雜旋轉和平移、條件數大幅提高和多函數鑲嵌等，從而使得這些基準函數不再關于某點對稱，其表達式高度復雜，理論全局最優解可隨機設置。這28 個基準函數共分3 類：第一類是由F1～F5 等5 個單峰函數組成，這些單峰函數包含有極高的條件數，主要用于測試算法的求精能力；第二類是由F6～F20 等15 個多峰函數組成，這些多峰函數是由上述著名的測試函數經旋轉平移后而形成，主要用于測試算法的探索能力；第三類是由F21～F28等8 個復合函數組成，這些復合函數是由若干個第一類和第二類函數經復雜鑲嵌而形成，其函數表達式異常復雜，主要用于同時測試算法的求精能力和探索能力的協調性。本文選擇了6 個代表性的基準函數，每類選2 個，如表5 所示。

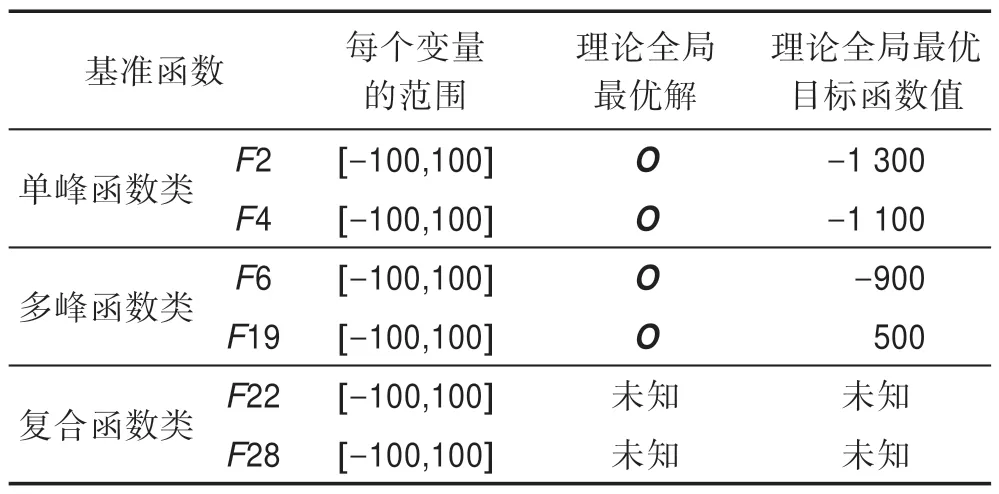
Table 5 Benchmark function optimization problems表5 基準函數優化問題

在表5 中，優化問題的維數為n；O是一個n維決策向量，O的值隨機產生。這些基準函數的形式可參見文獻[22]。

用HS-CBCO 算法去求解表5 所示的6 個基準函數，HS-CBCO 的參數設置為n=50，ε=10-10，K=10，L=3，E0=0.01，G=1010。與HS-CBCO 算法進行比較的優化算法為：RC-GA（real-coded genetic algorithm）[2]、DASA（differential ant-stigmergy algorithm）[4]、NP-PSO（non-parametric particle swarm optimization）[23]、MBBO（metropolis biogeography-based optimization）[9]、DE（differential evolution）[24]、SaDE（differential evolution algorithm with self-adaptive strategy）[25]和ABC（artificial bee colony algorithm）[11]。計算時，這7 種算法的參數按表6 進行設置。RC-GA 是一種新型實數編碼遺傳算法，其中的算子采用實數編碼設計，完全不同于傳統的GA 算法；DASA 是一種模仿蟻群算法的思路而完全重構的新型算法；NP-PSO 是一種不需要進行參數設置的粒子群算法；MBBO 對傳統的生物地理學算法的島嶼特征進行了大幅修改，強化了都市特征；DE 是在傳統差分進化算法中引入了局部誘導遺傳算子的新型差分進化算法；SaDE 在傳統自適應差分算法中引入了一種新的自適應參數控制策略；ABC 是在傳統蜂群算法中引入了基因組合的蜂群算法。這7 個算法是其對應傳統算法的較優改進版，特別適合求解高條件數單峰、多峰復合優化問題。

用這些算法獨立求解每個基準函數51 次，表7列出了最優目標函數的平均值（Average）、中位數（Median）、標準差（STD）、計算時間（Time），并對每種算法進行排序。表7 的Rank1 是按該算法的平均最佳目標函數值的精度進行的排名，Rank2 是按平均最佳目標函數的精度與平均計算時間的長短兩者綜合進行的排名。

Table 6 Parameter settings of compared algorithms表6 被比較算法的參數設置

從表7 可以看出各算法的排名按精度或按精度+計算時間的最終排名均為：

HS-CBCO>SaDE>DE>DASA>MBBO>ABC>NP-PSO>RC-GA

圖4（a）～圖4（f）說明各算法求解6 個基準函數時的樣本收斂曲線。為了突出這些樣本收斂曲線的變化，水平和垂直軸采用對數刻度。

6 HS-CBCO 算法的性能分析

6.1 求精和探索能力及其協調性分析

（1）求精能力分析。從圖4（a）～圖4（f）可知，HSCBCO 算法的收斂曲線在一些時間段內較其他算法的收斂曲線上升緩慢，且持續時間長。此說明HSCBCO 算法提升最優解精度的演化十分明確，該特征表明HS-CBCO 算法的求精能力較其他算法強。另外，由表7 可知，HS-CBCO 算法求解F2、F4、F6、F19時，能獲得其理論全局最優解；HS-CBCO 算法求解F22、F28 時，所獲得的全局最優解均優于其他被比較算法。此說明HS-CBCO 算法較其他被比較算法具有更好的求精能力。

（2）探索能力分析。從圖4（a）～圖4（f）可知，HSCBCO 算法的收斂曲線在一些時間段內較其他算法的收斂曲線陡，此說明HS-CBCO 算法提升IPI 指數的耗時很短，該特征表明HS-CBCO 算法探索新空間的能力較其他被比較算法更強。

（3）求精和探索能力的協調性分析。從圖4（a）～圖4（f）可知，與其他被比較算法相比，HS-CBCO 算法的緩（求精能力)和陡（探索能力)交替出現，且緩的持續時間均較長，陡的持續時間均較短，此表明HS-CBCO 算法的求精和探索能力的協調性均優于其他被比較算法。

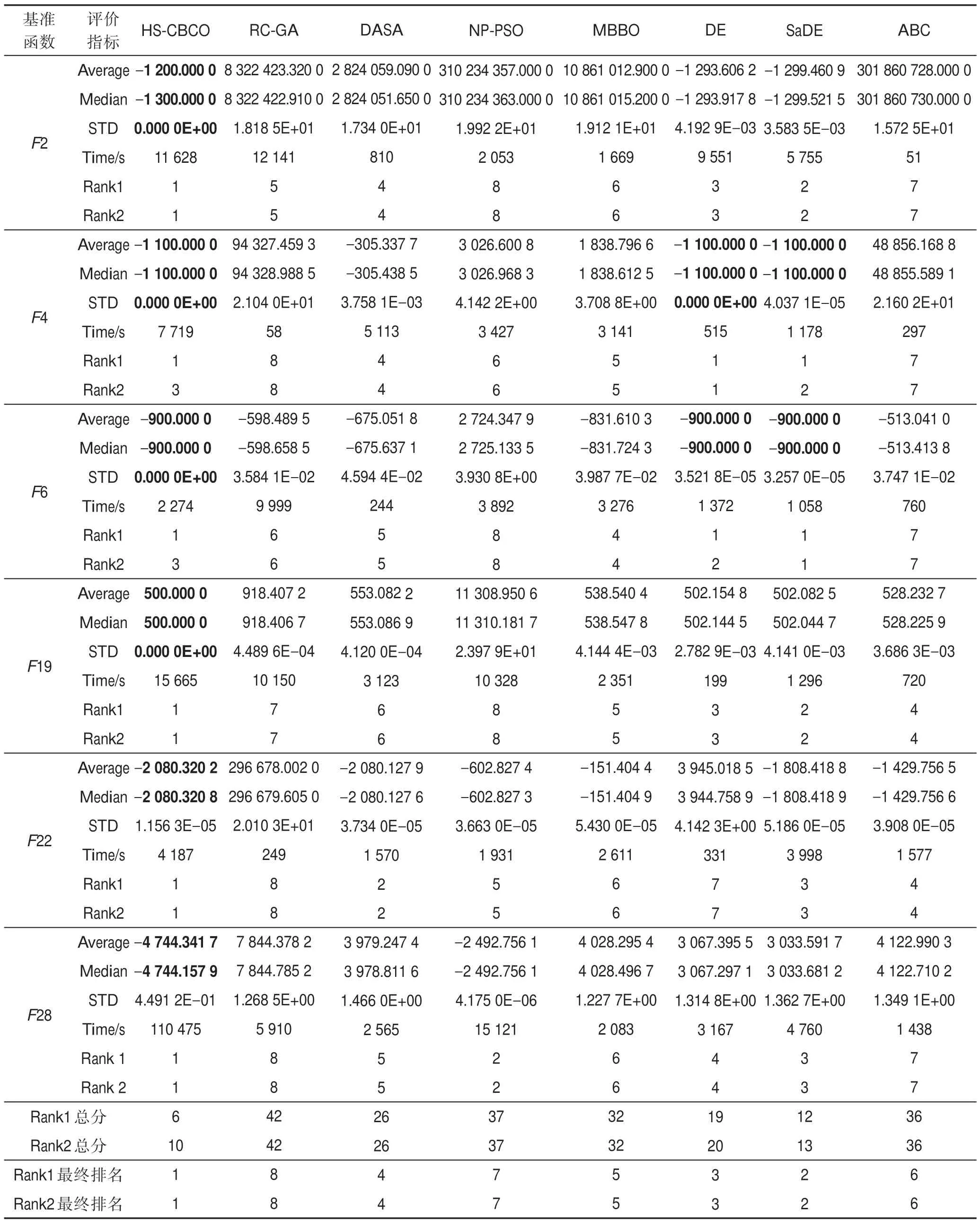
Table 7 Comparison of optimum solutions obtained by each algorithm表7 各算法求解結果的比較

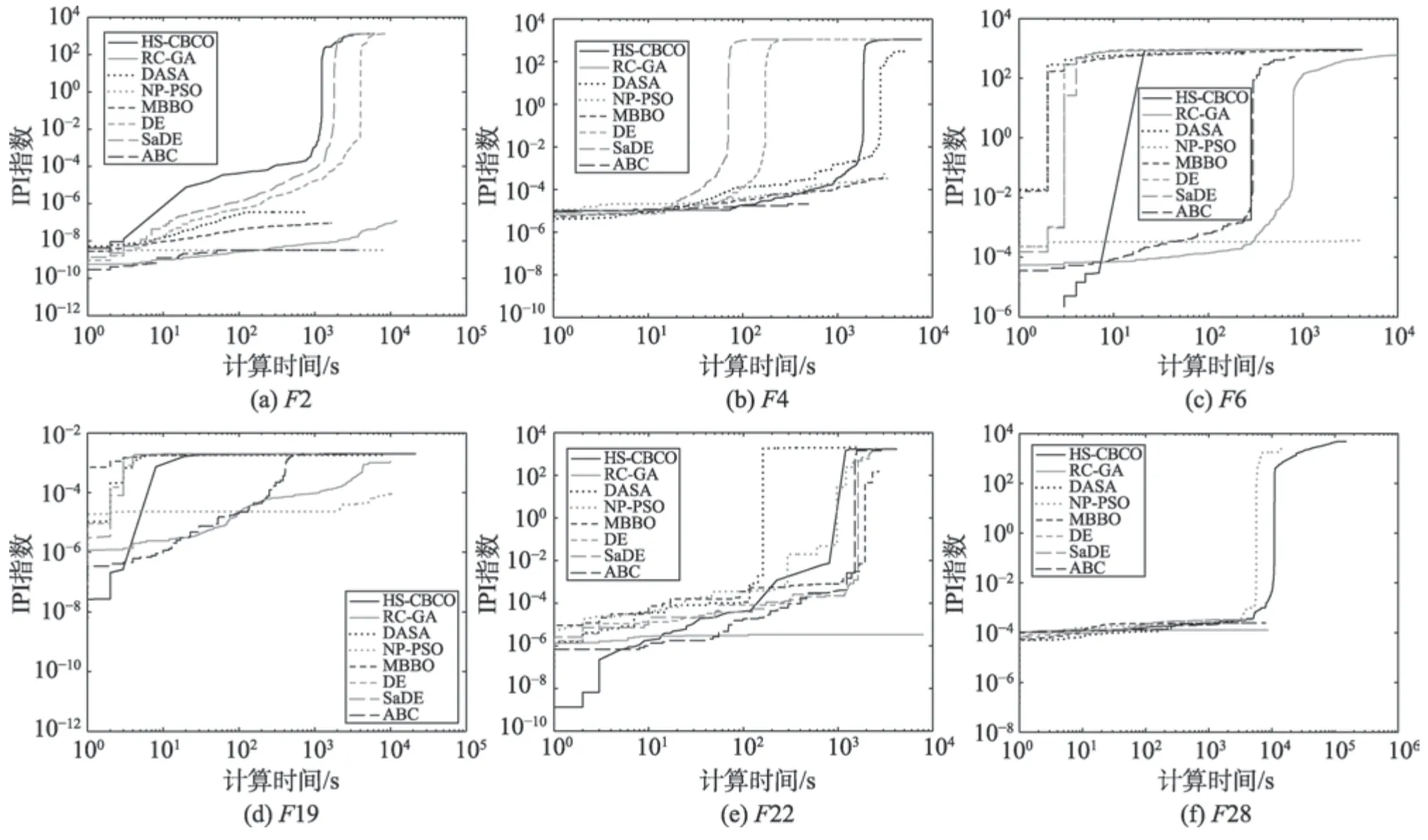
Fig.4 Sample convergence curves圖4 樣本收斂曲線

6.2 收斂性精度和收斂速度分析

（1）收斂性分析。從定理3 可知，HS-CBCO 算法具有全局收斂性；又從2.5 節知，HS-CBCO 算法具有“步步不差”特性，此表明HS-CBCO 算法的收斂過程不會出現忽大忽小的情形。從圖4 所示的樣本收斂曲線中的黑實線可知，HS-CBCO 算法的收斂過程與理論分析完全一致。

（2）收斂速度分析。在求解過程中，若HS-CBCO算法經常出現較陡的收斂曲線，說明HS-CBCO 算法的收斂速度較快。從圖4（a）～圖4（f）的黑實線可知，HS-CBCO 算法收斂較快。

（3）收斂精度分析。在求解后期，若HS-CBCO算法的收斂曲線上升緩慢，且持續時間長，說明HSCBCO 算法提升全局最優解精度的過程十分明確。從圖4（a）～圖4（f）的后段黑實線可知，HS-CBCO 算法均能獲得很高精度的全局最優解。

7 結束語

HS-CBCO 算法具有如下特點：

（1）HS-CBCO 算法依據水平結構競爭-互利群落動力學模型構造，可將生物個體科學地劃分成許多種類，從而大幅提升了生物個體的多樣性。

（2）HS-CBCO 算法依據水平結構競爭-互利群落動力學模型來確定生物個體數，從而使得生物個體數確定的科學性得到提升，避開了人為確定生物個體數的困擾。

（3）HS-CBCO 算法中運用水平結構競爭-互利群落動力學模型開發出了競爭算子、互利算子、普通影響算子和強烈影響算子。競爭算子和互利算子可實現個體跨種群交換信息，而普通影響算子和強烈影響算子可實現種群內部生物個體之間的信息交換，從而實現生物個體間信息的充分交換。

（4）HS-CBCO 算法的新生算子可適時補充新個體到種群中，而死亡算子可將種群中的虛弱個體適時清除掉，從而大幅提升算法跳出局部陷阱的能力。

（5）HS-CBCO 算法所涉及的參數的絕大部分依據水平結構競爭-互利群落動力學模型來確定，無需人為設置；而需要人為設置的參數卻很少，且易于設置。

（6）HS-CBCO 算法的求精能力和探索能力及其兩者的協調性均優良。

（7）HS-CBCO 算法的演化過程具有Markov 特性和“步步不差”特性，從而使得該算法具有全局收斂特征。

（8）HS-CBCO 算法具有科學理論作為支撐，易于進行深入分析。

HS-CBCO 算法今后的改進方向如下：

（1）深入研究各算子的動態特征。

（2）深入研究算法在求解過程中各種群的動態特征。

（3）對HS-CBCO 算法進行改進，使之適應復雜水平結構種群競爭、互利環境。