支承間距對十一柱塞航空液壓泵轉子系統臨界轉速的影響分析

郭長虹1 王嘉維1，白如霞1，權凌霄23

(1．燕山大學 機械工程學院，河北 秦皇島 066004；2．燕山大學 河北省重型機械流體動力傳輸與控制實驗室，河北 秦皇島 066004;3．燕山大學 先進鍛壓成形技術與科學教育部重點實驗室，河北 秦皇島 066004)

引言

民機液壓系統不斷追求高壓、高速、高功重比的目標，對航空泵性能提出更為嚴峻的要求[1]。我國航空柱塞泵生產技術落后，民機航空泵完全依賴于進口，購置及維修價格昂貴、供貨周期長；我國僅有能力生產軍用柱塞泵，且產品性能與國外存在較大差距[2]，嚴重制約國內大飛機事業的發展。目前，國內外眾多科研工作者，采用轉子動力學理論分析復雜旋轉機械的動力學特性，如航空發動機、離心泵、汽輪機等，并取得一定的研究成果[3]，然而，鮮有學者采用轉子動力學理論研究柱塞泵的動力學特性。因此，本研究擬抽取泵旋轉部件構建其轉子系統模型，采用轉子動力學理論，研究泵轉子系統臨界轉速機理及其影響因素，以提高泵臨界轉速。

近年來，國內外專家對轉子系統臨界轉速分析及產生機理方面開展了很多研究工作，并取得顯著的進展。鄧旺群等[4-7]以發動機低壓轉子為研究對象，采用SAMCEF/ROTOR軟件分析其臨界轉速機理，研究結果表明，轉子臨界轉速隨軸向支承間距的減小而增加，但是影響程度較小。轉子系統第一階和第二階臨界轉速隨著懸臂長度的增大而減小。宋雪萍等[8]經研究發現，系統臨界轉速與支承剛度成正相關。但是，當剛度為108N/m時，臨界轉速的變化很小。喬曉利等[9]認為軸承等效剛度參數的改變，對電主軸轉子臨界轉速的影響較大，而等效阻尼參數與之相反。代彥賓等[10]研究得出，轉子系統第一階臨界轉速值與軸承預緊力成正相關，與軸承支承跨距成負相關。權凌霄[11]以斜盤式軸向柱塞泵-電機組轉子系統為研究對象,分析轉子系統臨界轉速及流量脈動及側向徑向壓力引起的不平衡響應。XING Z等[12]精確計算高速電機轉子臨界轉速，結果表明，改變軸承剛度和轉子材料可以調節轉子臨界轉速。CHIANG H等[13]以雙轉子系統為研究對象，研究發現轉速比參數對于雙轉子系統設計極為重要。

1 泵轉子系統集中質量模型建立

現抽取十一柱塞航空泵的旋轉部件組成航空泵轉子系統。根據離散等效原則，對航空泵傳動軸、輸入軸、旋轉組件及軸承進行等效簡化，構建航空泵轉子系統的集中質量模型。

1.1 十一柱塞航空泵工作原理及結構分析

航空泵通常將電機軸和泵軸通過花鍵或減速齒輪直接相連，省去聯軸器環節。十一柱塞航空泵三維模型如圖1所示。

圖1 十一柱塞航空泵三維模型

航空泵轉子系統由輸入軸、傳動軸、旋轉組件、軸承1及軸承2組成。不考慮軸承結構的影響，滾動軸承僅提供剛度，阻尼不計。航空泵各部件材料如表1所示。

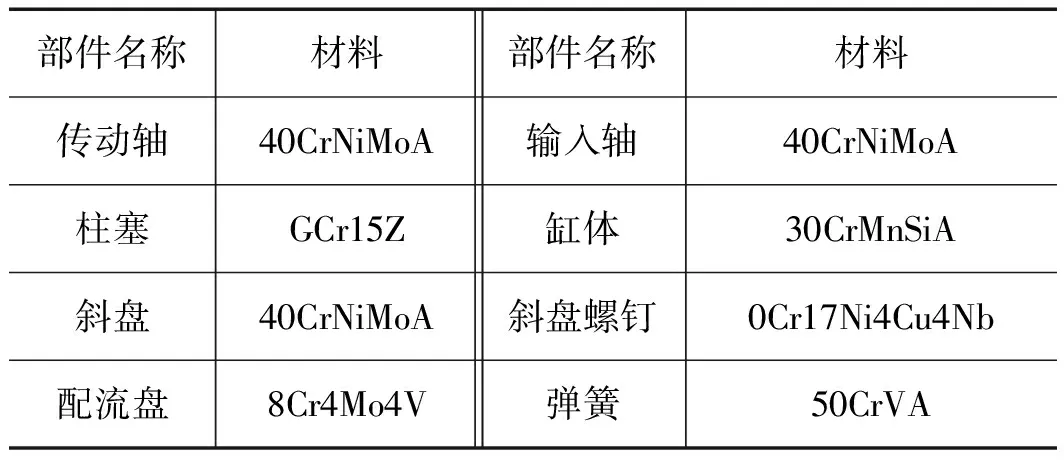
表1 航空泵各零件材料

1.2 航空泵轉子系統集中質量模型

根據航空泵轉子系統各部件的結構尺寸，建立其集中質量模型，首先應對轉子進行結點劃分。本研究重點研究斜盤傾角β為0時的轉子系統簡化模型。建模假設條件如下：

將旋轉組件視為整體，等效為一個質心處的剛性薄圓盤；僅研究航空泵轉子系統的橫向彎曲振動；將泵傳動軸和輸入軸視為整體，不考慮傳動、倒角的影響；支承中心位置不變，簡化為等剛度的線性彈性支承。

航空泵傳動軸離散的29個結點命名“1～29”，泵輸入軸離散22個結點命名為“30～51”，旋轉組件離散結點命名為“52”。根據各單元的長度等參數，將泵傳動軸和輸入軸視為整體，則整體集中質量模型如圖2所示。

圖2 航空泵轉子系統整體集中質量模型

由圖2可知，航空泵轉子系統的整體集中質量模型由52個具有質量和轉動慣量的結點、51段無質量彈性軸組成。此時，軸承1位于結點2處，軸承2位于結點21處，支承剛度取值為106N/m。

2 泵轉子系統臨界轉速數值分析

在所建立的航空泵轉子系統集中質量模型的基礎上，采用兩種傳遞矩陣法分析航空泵轉子系統的臨界轉速。修正軸承1的軸向支承位置、軸承2的軸向支承位置參數，從數學模型角度分析軸向支承位置參數對航空泵轉子系統臨界轉速的影響規律。

2.1 傳遞矩陣法分析轉子系統臨界轉速

按照復雜轉子系統的離散等效原則，建立實際轉子系統集中質量模型。采用兩種傳遞矩陣法分析航空泵轉子系統臨界轉速，并對比兩種分析方法的計算誤差。

1) Prohl傳遞矩陣法分析臨界轉速

實際轉子系統離散化后由N個單元組成，其集中質量模型如圖3所示。第N個單元的長度lN=0。

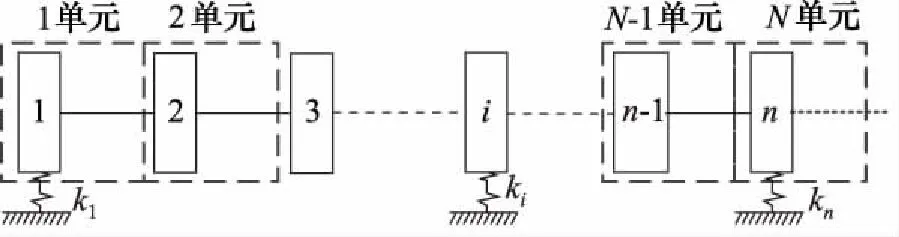
圖3 實際轉子系統的集中質量模型

若轉子系統最左端面為起始截面，其狀態向量為Z1，則任意截面的狀態變量Zi(i=2，3，…，N+1)可表示為：

Zi=Ti-1Zi-1=Ti-1Ti-2Zi-2=Ti-1Ti-2,…，T2T1Z1

=Ai-1Z1

初始截面的狀態變量，即為轉子系統的邊界條件，表示為：

(1)

對于任意截面i(i=2，3，…，N+1)，有：

(2)

對于末端截面N+1，有:

ZN+1=ANZ1

(3)

第N+1個單元左側的邊界條件為:

MN+1=0；QN+1=0

(4)

(5)

能使式(5)成立的ω值，即為轉子系統的臨界角速度。若式(5)有非零解，則應保證Δ(ω2)=0，即:

(6)

其中，Δ(ω2)稱為剩余量。

臨界轉速為：

(7)

2) Riccati傳遞矩陣法分析臨界轉速

對于大型軸系系統而言，傳統Prohl傳遞矩陣法的計算精度隨著計算頻率的提高而降低。在此方法的基礎上，進一步提出Riccati傳遞矩陣法，以提高數值分析穩定性。首先將狀態變量中的r個元素分為兩組，即:

(8)

其中，f由狀態變量中的r/2個零值組成，e由狀態變量中的其余r/2個非零值組成。轉子系統左側端面的邊界條件表示為M1=0,Q1=0，則:

(9)

對于相鄰的兩截面，其狀態變量可表示為:

(10)

令Si為Riccati傳遞矩陣，是r/2階方陣。引入Riccati變換fi=Siei，則:

(11)

整理式(11)，得:

fi+1=(u11S+u12)i(u21S+u22)iei+1

(12)

又fi+1=Si+1ei+1，故:

(13)

對于起始截面，S1=0，由式(13)可得S2，S3，…，SN+1。對于末端截面，有:

fN+1=SN+1eN+1

(14)

式fN+1=SN+1eN+1=0有解的條件是|S|N+1=0。2.2 MATLAB求解轉子系統臨界轉速

MATLAB編程求解臨界轉速流程圖，如圖4所示。

取2個角速度值，計算對應剩余量。若剩余量異號，則臨界角速度存在于2個角速度值的區間內。確定臨界角速度所在范圍后，采用二分法即可不斷逼近求出臨界角速度，滿足的值即為臨界角速度。

1) Prohl傳遞矩陣法臨界轉速分析

采用Prohl傳遞矩陣法求解航空泵轉子系統前兩階臨界轉速時，分別考慮有無剪切效應的影響；Prohl傳遞矩陣法剩余量曲線如圖5和圖6所示。

由剩余量曲線圖可得，當考慮剪切效應系數的影響時，航空泵轉子系統的前兩階臨界轉速值分別為10912.46 r/min和16493.98 r/min； 當不考慮剪切效應系數的影響時，航空泵轉子系統的前兩階臨界轉速值分別為10919.2 r/min和16514.95 r/min。

圖4 MATLAB數值分析流程圖

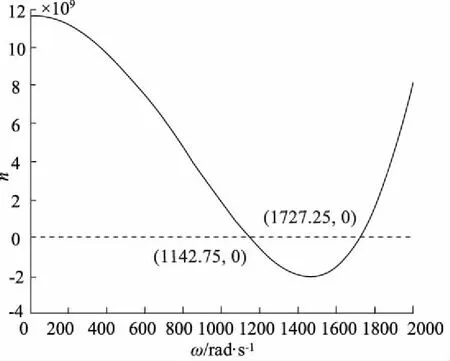
圖5 考慮剪切效應系數

圖6 不考慮剪切效應系數

2) Riccati傳遞矩陣法臨界轉速分析

采用Riccati傳遞矩陣法研究航空泵轉子系統臨界轉速時，有無剪切效應影響剩余量曲線如圖7和圖8所示。

圖7 考慮剪切效應系數

圖8 不考慮剪切效應系數

當考慮剪切效應系數的影響時，航空泵轉子系統的前兩階臨界轉速值分別為10910.07，16496.41 r/min；當不考慮剪切效應系數的影響時，航空泵轉子系統的前兩階臨界轉速值分別為10919.62，16515.51 r/min。

2.3 軸向支承位置對系統臨界轉速的影響

初始時，軸承1位于結點2處的圓盤，軸承2位于結點21處的圓盤；本節分別將軸承1的軸向支承位置調整至結點1處和結點3處，將軸承2的軸向支承位置調整至結點25處。考慮剪切效應系數的影響，采用Prohl傳遞矩陣法求解航空泵轉子系統的前兩階臨界轉速值，研究其變化趨勢。

(1) 軸承2位置不變，軸承1位置前移9.1 mm至結點1處、后移9.1 mm至結點3處，此時剩余量曲線分別如圖9和圖10所示。

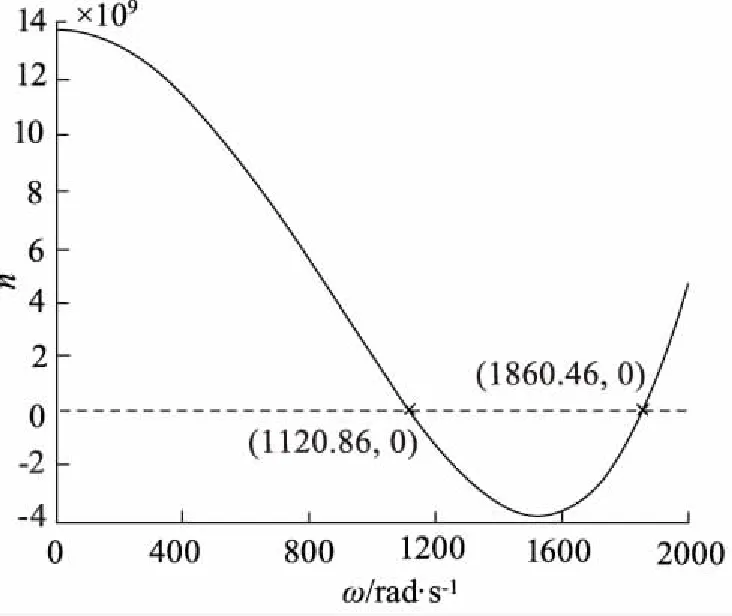
圖9 前移9.1 mm

圖10 后移9.1 mm

由圖9和圖10剩余量曲線可得，軸承1位置前移9.1 mm至結點1處、后移9.1 mm至結點3處，第一階臨界轉速變化量分別為-209.08 r/min和+218.75 r/min;第二階臨界轉速變化量分別為+1273.01 r/min和-1425.87 r/min。由分析可得，系統第一階臨界轉速增加，第二階臨界轉速降低，且該參數對第二階臨界轉速的影響更為明顯。

(2) 軸承1位置不變，軸承2位置后移11.7 mm至結點25處，此時剩余量曲線分別如圖11所示。

圖11 軸承2位置變化剩余量曲線

軸承2位置后移11.7 mm至結點25處，第一階臨界轉速變化量為+297.94 r/min;第二階臨界轉速變化量為+1302.35 r/min；當軸承1位置不變，軸承2軸向支承位置在一定范圍內后移時，航空泵轉子系統第一階、第二階臨界轉速均增加，且該參數對第二階臨界轉速的影響程度更大。

軸承支承位置的改變將影響軸承支承跨距。軸承1后移時，兩軸承支承跨距減小，第一階臨界轉速增加，軸承2后移時，兩軸承支承跨距增加，但第一階臨界轉速同樣會增加，因為軸承2后移時，對應的轉子右側懸臂端長度減小，此時懸臂端長度成為影響臨界轉速的關鍵因素之一。

3 轉子系統臨界轉速驗證實驗

在“MFS-RDS機械故障診斷和轉子動力學模擬實驗平臺”上完成臨界轉速驗證實驗。針對實驗轉子系統模型，按照本研究提出的離散等效原則，建立其集中質量模型，數學模型分析與實驗相互驗證，以證明本研究轉子系統集中質量模型建立及求解的正確性。此外，在簡易轉子實驗臺上完成支承軸承位置對臨界轉速影響規律的驗證。

3.1 MFS-RDS實驗平臺介紹

MFS-RDS實驗平臺可用于研究轉子動力學特性、旋轉機械故障診斷等，可完成轉子系統臨界轉速實驗，如圖12所示。

圖12 MFS-RDS實驗平臺

3.2 轉子系統臨界轉速測試及分析

由圖12可知，利用卡環將圓盤安裝于轉軸上，轉軸兩端安裝軸承，3個加速度傳感器分別位于軸承座3個方向。對加速度測試數據進行FFT頻譜分析，轉子系統瀑布圖如圖13所示。

可以看出，通過測試轉子系統振動，獲得系統的一階固有頻率54.41 Hz，對應第一階臨界角速度341.87 rad/s，第一階臨界轉速3264.60 r/min。

3.3 傳遞矩陣法求解實驗轉子系統臨界轉速

將MFS-RDS轉子系統按所述方法進行離散等效，建立其集中質量模型。分別采用Prohl傳遞矩陣法和Riccati傳遞矩陣法分析轉子系統臨界轉速，剩余量曲線如圖14和圖15所示。

圖13 轉子系統瀑布圖

圖14 Prohl傳遞矩陣法剩余量曲線圖

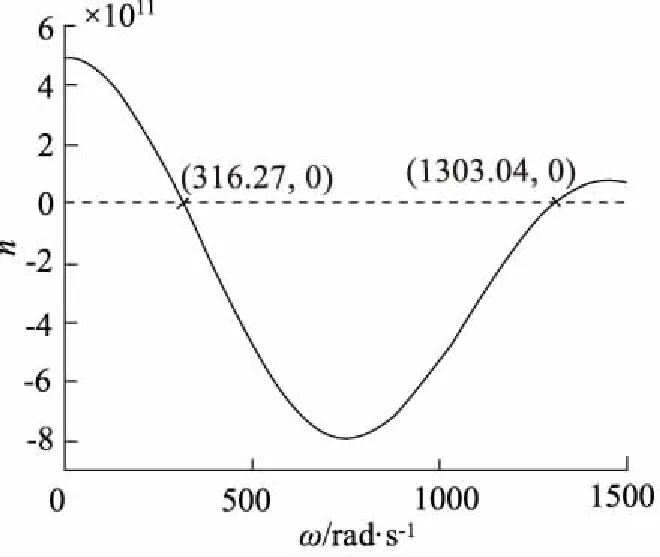
圖15 Riccati傳遞矩陣法剩余量曲線圖

采用數學模型及實驗測試兩種方法分析實驗轉子系統臨界轉速，如表2所示。

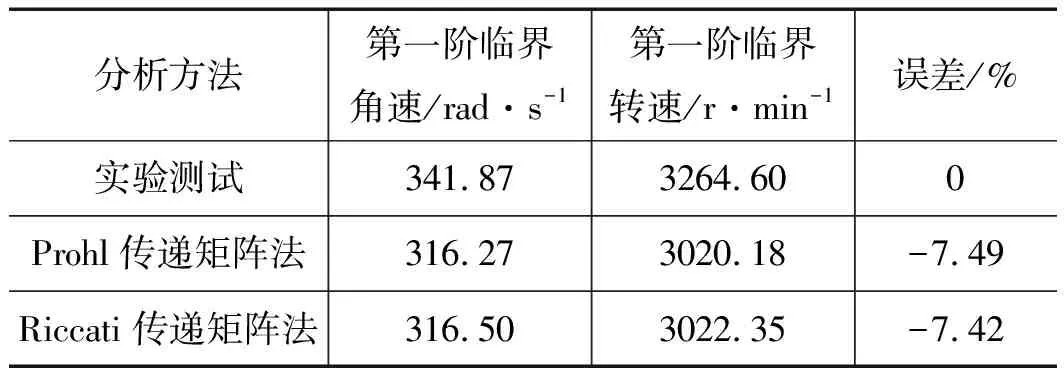
表2 實驗轉子系統臨界轉速對比

由表2可知，采用數學模型和實驗測試兩種方法所求解的第一階臨界轉速誤差為7.5%左右。結果表明實驗結果與數學模型分析結果具有一致性，驗證了本研究集中質量模型建立及求解方法的準確性。

3.4 軸承軸向支承位置對臨界轉速的影響

為驗證軸承軸向支承位置對干轉子系統臨界轉速的影響，現搭建簡易轉子系統實驗臺，該實驗臺由電機、轉軸、圓盤、軸承、聯軸器等組成，如圖16所示。

圖16 簡易轉子系統實驗臺

本研究主要關注各參數對干轉子系統臨界轉速的影響。現保持圓盤及軸承1的所處位置不變，調整軸承2的軸向支承位置，使兩軸承間距分別為700，600，500 mm，進行臨界轉速測試。

對加速度實測數據進行降噪處理，對降噪后的測試數據進行FFT頻譜分析，轉子系統瀑布圖如圖17～圖19所示。

圖17 轉子系統瀑布圖(軸承間距700 mm)

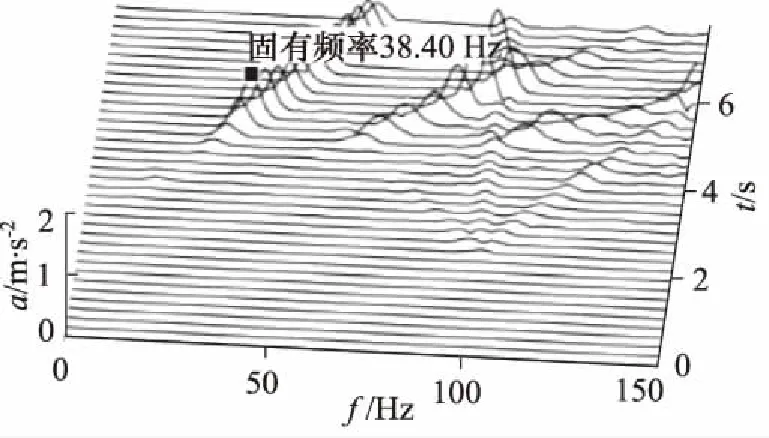
圖18 轉子系統瀑布圖(軸承間距600 mm)

當軸承的軸向支承位置發生改變時，兩軸承間距隨之改變。由圖17～圖19知，當軸承間距減小時，實驗轉子系統的第一階臨界轉速增加。

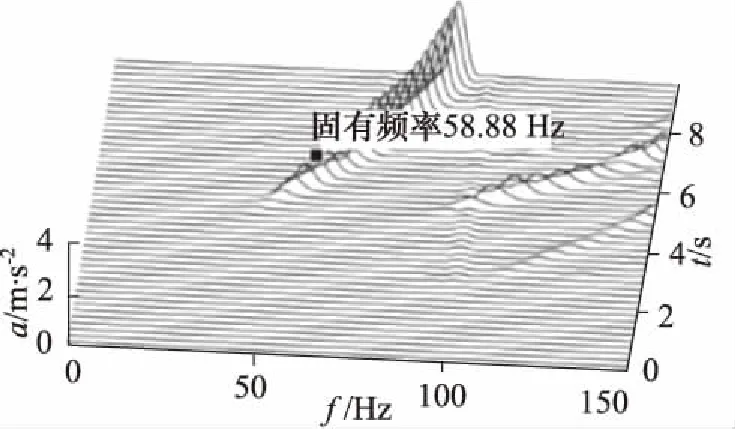
圖19 轉子系統瀑布圖(軸承間距500 mm)

4 結論

本研究依據離散等效原則建立航空泵轉子系統集中質量模型，采用傳遞矩陣法分析其臨界轉速；通過修正軸向支承位置等參數，得到以下結論：

(1) 分別采用Prohl傳遞矩陣和Riccati傳遞矩陣分析航空泵轉子系統臨界轉速，分析結果基本一致；

(2) 分別改變軸承1和軸承2的軸向支承位置，結果表明，軸承1軸向支承位置后移時，航空泵轉子系統第一階臨界轉速增加。軸承2軸向支承位置在一定范圍內后移時，轉子系統第一階臨界轉速均增加，且軸向支承位置參數對第二階臨界轉速的影響程度更大；

(3) 建立實驗臺轉子系統集中質量模型，實驗測得臨界轉速值與數學模型求解臨界轉速值誤差在7.5%左右，驗證了數學模型建立的準確性；在簡易轉子實驗臺上完成軸向支承位置對轉子系統臨界轉速的影響驗證，研究表明，支承間距減小，轉子系統第一階臨界轉速增加。