復頻條件下組合接收參數設計

徐 峰 劉福烈 王 渝 閔鑫林 徐吉松

(西南石油大學地球科學與技術學院，四川成都 610500)

0 引言

20世紀30年代，在地震勘探中，地球物理學家們將幾個檢波器接收的數據疊加起來作為一道數據輸出，大幅度地提高了地震資料信噪比，于是有關“組合”的理論研究和實踐便在地球物理領域逐漸展開。組合內檢波器數目、組內距、各檢波點接收到信號的能量加權和延時量是組合響應函數的四種重要自變量，也是組合參數設計的主要內容。

早期的地震數據現場采集一般只考慮檢波器數目、組內距對信噪比的影響。Klipsch[1]從統計學角度給出了信噪比與組合個數間的關系； Johnson[2]基于天線理論推導了組合響應函數的表達式，奠定了地震勘探組合理論基礎； Dean等[3]分析了地震記錄中相干噪聲強度與模擬檢波器個數和間距的關系，通過獲取檢波器間相關系數尋求最佳間距，進而壓制相干噪聲和背景噪聲。

針對加權系數設計： Holzman[4]提出了切比雪夫多項式加權組合方式，因其具有可調節的壓制比、最窄的通放帶寬度及壓制帶極值均勻相等的特點而受到廣泛關注； Rietsch[5]改進了切比雪夫多項式權系數計算公式，在確保計算精度前提下，提高了計算效率； Simaan[6]提出了一種最佳組合濾波器設計方法，在頻率域以約束計算量和檢波器數量最小化來確定權系數，對于相干噪聲壓制和頻率選擇效果明顯且成本較低； Hanna[7]將多重衰減條件應用于組合權系數與延時量計算，從多重相干干擾和隨機噪聲中提取反射信號。

對于延時組合： Johnson[8]根據近地表噪聲與有效波到達檢波器的時差，由檢波器位置確定延時量，通過延時疊加提升信噪比； King等[9]采用選取參考道與各獨立地震道做互相關的方法確定延時量，用于地震數據組合疊加； Mao等[10]通過線性化波形反演技術同時估計組合的延時量和權系數； Bagaini[11]基于系數矩陣構建各檢波器延時量、接收時差的方程，通過最小二乘法求解延時量，證明在低信噪比條件下也能較準確地估計延時量。

調研以往相關研究成果，發現組合問題涉及的四種參數雖都已被較詳細地探討過，但仍存在幾方面的不足： 首先，因組合設計的目的不同，四種參數鮮有被綜合考慮，如Dean等[3]是以相關系數大小設計組合個數和間距，Holzman[4]是以控制通放帶形態設計組內距和加權系數，Simaan[6]以檢波器數量最小化確定權系數，Hanna[7]設計組合權系數與延時量是為了壓制隨機噪聲等； 其次，參數設計時未考慮頻率，如Mao等[10]以波形反演技術估計組合的延時量與權系數，或未考慮復頻地震波的頻率差異，如在切比雪夫多項式權系數設計中被壓制的頻率成分都是等權重的； 再次，參數設計并沒有遵循特定的目標函數，如韋成龍等[12]是以限定子波主峰同相疊加時差小于某約定值來設定海洋立體槍陣延時量，張鵬等[13]在設計海上空氣槍點震源時忽略了子波和能量的方向性差異，何寶慶等[14]在研究寬線采集數據的組合時討論了線距、線數、孔徑、信號頻率等參數，雖給出了寬線采集系統的響應函數，但未給出這些組合參數設計的依據函數。

“組合”本身不可避免地會引起低通濾波效應，同時伴隨AVO響應的畸變。若未綜合考慮參與組合的各類因素，可能還會加劇這一問題。本文從具有復頻性質的地震波組合響應入手，建立包含四種組合參數的目標函數，通過全局尋優實現設計，期望對地震數據進行室內組合時，能在提高信噪比的同時減弱低通濾波效應和AVO畸變現象。

1 組合參數設計

相控理論源于雷達設計，意指通過控制不同組合單元發射/接收簡諧波的相位，達到控制組合整體輸出響應形態的目的。在初相位一致、頻率穩定前提下，相位控制就轉化為各子單元的時差控制。

1.1 組合響應

姜弢等[15]給出了單頻簡諧波的組合響應函數。設組合內有N個檢波器，相鄰檢波器間距為d，當波長為λ的平面簡諧波以與豎直方向呈θ角入射到組合內時，疊加后的能量響應可表示為

(1)

式中：i為檢波器編號； j為虛數單位；f為簡諧波頻率；v為地震波速度； Δφ為相鄰檢波器接收相位差；αi為加權系數，在采集現場組合中因不能改變各檢波器輸出能量比例，故通常設定αi=1。

根據歐拉公式，將式(1)分解為

(2)

顯然，當θ=0°時，該組合響應F(θ)=1。

如圖1所示，檢波器組合實際上是方向濾波器，響應因子取值區間是0～1。F(θ)=1表示來自θ方向的地震波是全通放的，F(θ)=0代表該角度方向能量全壓制。當地震波的頻率和傳播速度確定后，視波數(k*=f/v·sinθ)是入射角θ的函數，故組合接收也是視波數濾波。

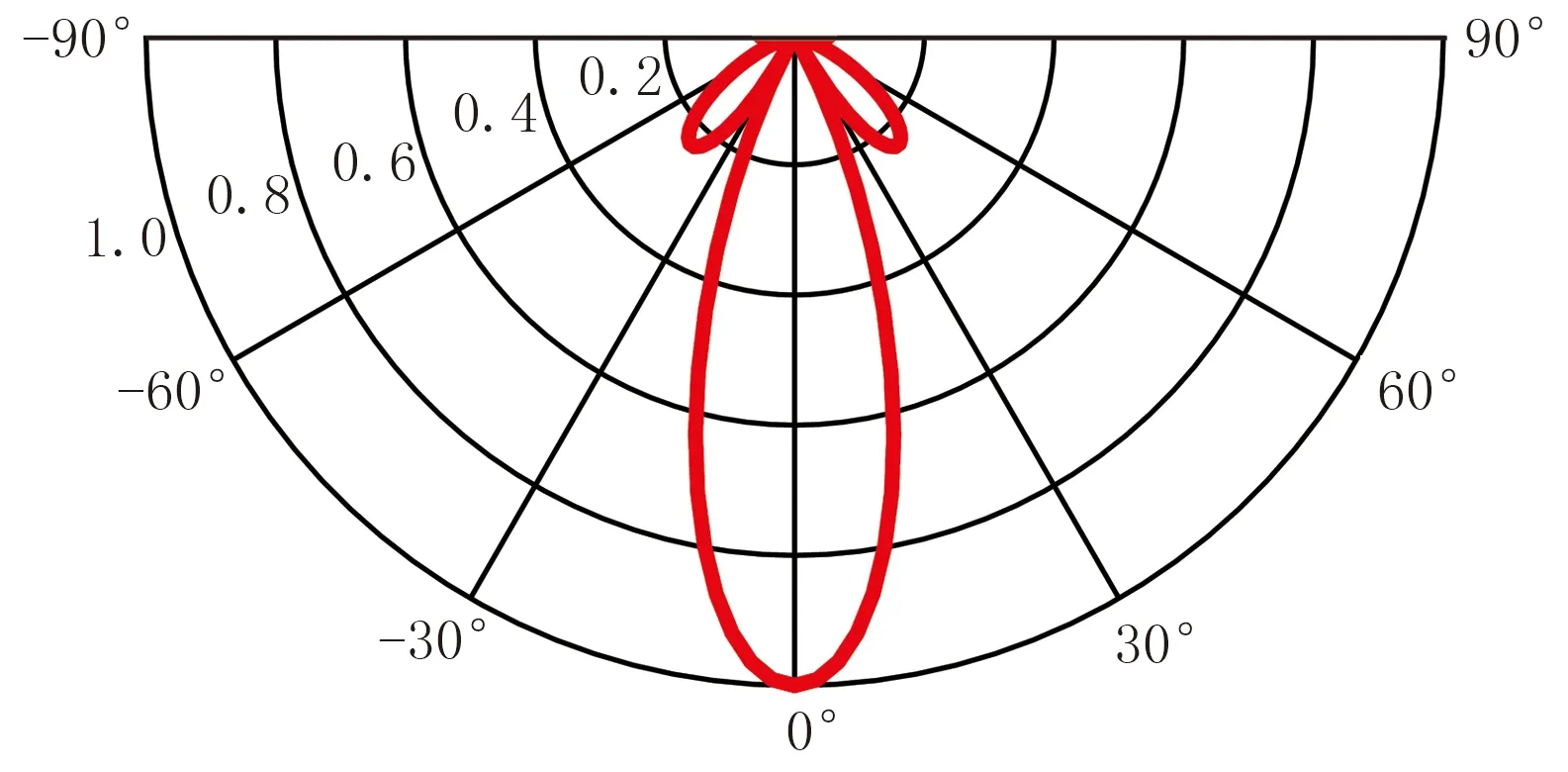
圖1 簡諧波組合能量響應

對于具有一定頻寬的地震子波，其組合響應為多個頻率成分各自組合響應的線性加權疊加，則地震子波的組合響應為

(3)

式中：fmin、fmax分別為頻帶寬度內的最小和最大頻率；fl為該頻帶內某單一頻率；S(fl)為子波各頻率成分的權系數。若接收子波為Ricker子波，則S(fl)可用其振幅譜表達為

(4)

式中fm為Ricker子波主頻。

在進行室內組合時，可靈活設置組內各道的能量比例，即不再限定αi=1。若假設各檢波器接地耦合性一致，則同一子波到達組內各檢波器的相位差Δφ可由接收時間差Δt替代，即Δφ=2πflΔt。

綜合式(1)和式(3)，可推導出不等權組合響應

(5)

1.2 組合參數設計

反射地震勘探中，噪聲和有效信號到達地表時入射角具有差異：噪聲主要來源于近地表，入射角較大； 反射信號來自一個錐角區間，入射角隨炮檢距增大而增大，隨目的層加深而減小(圖2)。當目的層傾斜時，上傾方向入射角會大于下傾方向；當淺地表存在低降速帶，入射角又會進一步減小，即實際入射角會因地層構造形態和檢波器在排列中位置的不同而有差異，是時、空變的。為簡化計算，應用中可估算一個最大反射角，將盡可能多地囊括反射信號，該入射角通常由中、深目的層深度H和排列長度L求得

(6)

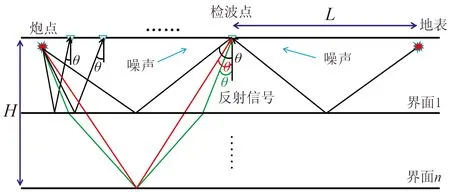
圖2 檢波點入射信號分布示意圖

圖3 復頻子波組合能量響應

當有效信號最大入射角度確定后，即可據此設計組合參數。理想的組合效果是將噪聲成分完全壓制掉，有效信號部分充分保護起來，即一個“門”式濾波響應(圖3中藍線)。這在實踐中難以實現，尤其是考慮到應用中有限的組合個數和較大組內距的實情。參考圖3中的復頻能量響應(紅線)，在“門”內除0°外其他角度也會被不同程度地壓制(此即組合會損傷有效波的緣由)，而在“門”外，噪聲也會被通放。因此，更現實的方案是摒棄絕對壓制思路，尋求信噪比相對改善——采用有效信號區與噪聲干擾區的能量比值最大來設計組合參數，該比值被稱為理論信噪比。

統計反射波入射角度范圍內能量總和

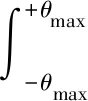
(7)

將Es與干擾波入射范圍內能量總和En之比值，定義理論信噪比

(8)

式中E為檢波器接收全空間范圍內能量總和。

將式(7)代入式(8)，可得

(9)

在該式中：當傳播速度v、頻率權系數S、L和H確定以后，參照式(5)，影響P取值的就是組合個數N、組合加權系數α、組內距d、延時量Δt，因此求解目標函數max{P(N,d,α,Δt)}即變為

(10)

直接給出式(10)的解析解是困難的，實際求解采用數值逼近法。同時，根據徐峰等[16]相控組合理論，為了不出現非設計方向的能量泄漏(噪聲區能量響應因子值極大)，組內距、組合個數、地震波主波長三者之間應滿足

dN<λ

(11)

聯合式(10)與式(11)，即可確定最優組合參數。

2 數值模擬

設計的二維地震地質模型(圖4)的尺寸為1200m×600m，包含三套水平地層，采用主頻為30Hz的雷克子波，震源置于(600m，10m)處，檢波器排列鋪設于地表。

通過波動方程正演，得到單炮記錄(圖5a)； 然后在上述模型地表向下15m處均勻布設高速散射點(圖4中黑點，v=1600m/s)，模擬繞射源，加入60%隨機噪聲后再次正演得到圖5b； 基于圖5b分別得到常規組合(圖5c)、延時等權組合(圖5d)、延時加權組合(圖5e)、F-K濾波后(圖5f)的模擬單炮記錄及對應的組合中被壓制的噪聲成分(圖6)。

圖4 三層二維地震地質模型

2.1 常規組合

在地震數據現場采集中，常規組合僅考慮檢波器個數N和組內距d兩個參數。根據模型參數，用式(6)算得接收有效波最大角度為26.6°，以理論信噪比P值最大為目標函數，兼用式(11)作為約束條件，計算得到最優組合參數為N=7、d=5。

從常規組合的模擬單炮記錄(圖5c)并結合圖6a可見： 常規組合對于散射干擾和隨機干擾均有相當不錯的壓制效果，但對有效信號的損傷也較大。

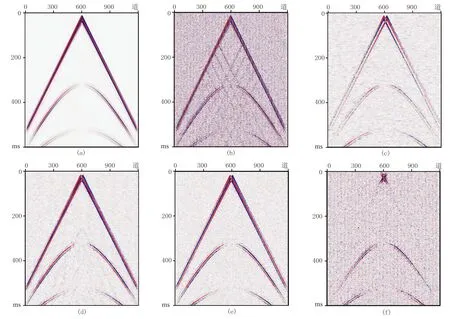
圖5 原始及組合處理后的模擬單炮記錄

再從各套組合數據第350道歸一化頻譜分析(圖7)及第二反射層AVO曲線統計(圖8)中，可看到常規組合的低通特征明顯、AVO畸變嚴重。

2.2 室內多參數組合

與現場組合相比，室內組合更靈活。例如：可對檢波器個數N、延時量Δt、組內距d及加權系數αi四種參數同時進行設置； 下面分別進行不考慮權系數變化的延時等權組合和考慮權系數變化的延時加權組合參數設計(表1)。

從延時等權組合后的模擬單炮記錄(圖5d)并結合圖6b可知，延時組合能同時壓制背景噪聲和散射噪聲，對有效波的損傷小于常規組合。

延時加權組合通過同時控制延時量和加權系數，可提高理論信噪比。從延時加權組合后模擬單炮記錄(圖5e)并結合圖6c可知，與常規組合和延時等權組合相比，延時加權組合后散射干擾與背景噪聲進一步被壓制，有效信號損傷更?。?另外，從圖7、圖8中可見該組合的頻帶特征基本保持與原始資料一致，且AVO畸變較小。

圖6 模擬記錄中壓制的噪聲

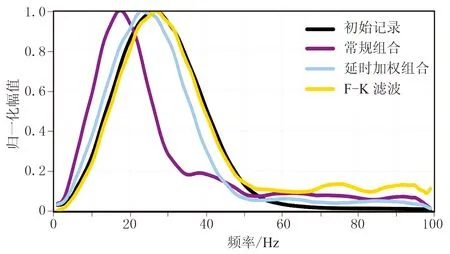
圖7 第350m檢波道記錄頻譜分析

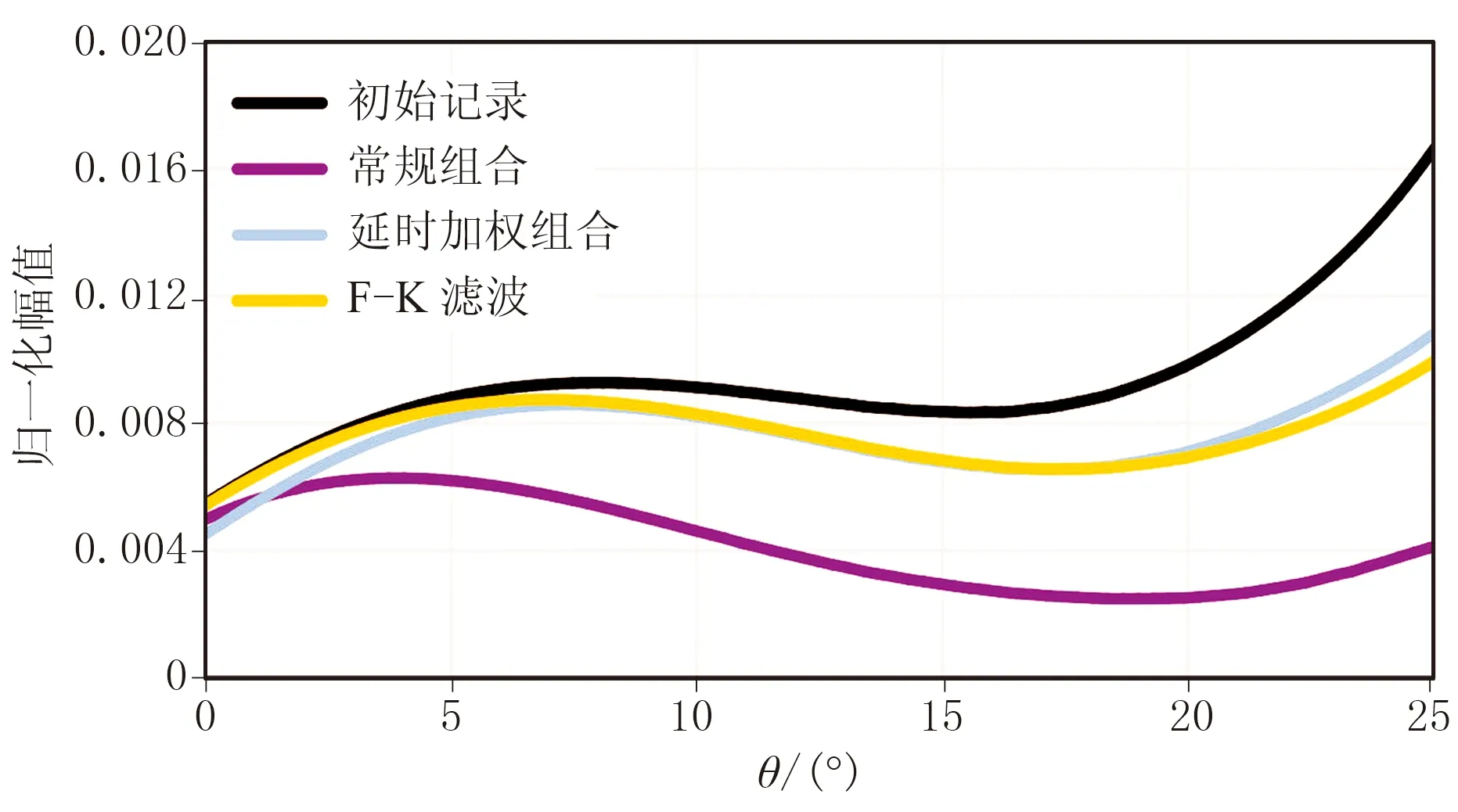
圖8 模擬記錄第二層反射AVO曲線

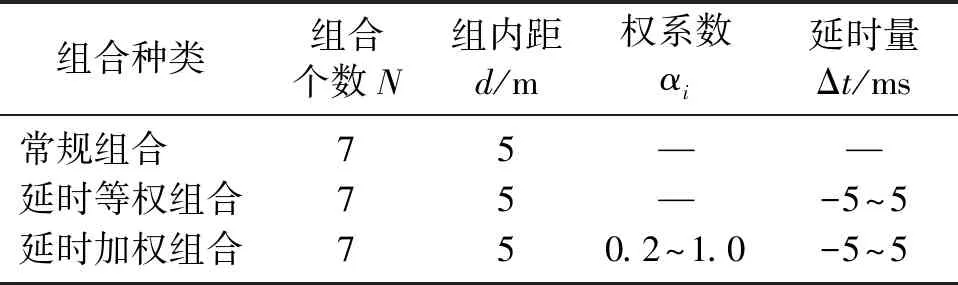
表1 組合參數優化計算結果

2.3 F-K濾波

F-K濾波作為一種常用的室內資料處理手段，是根據噪聲干擾與有效波在視速度和頻率上的差異進行濾波。

從F-K濾波結果(圖5f)并結合圖6d可見：與延時加權組合相比，F-K濾波較好地壓制了散射干擾，但因散射干擾傾角與直達波傾角、遠炮檢距有效波傾角近似一致，難以避免地對直達波和有效波也進行了一定程度壓制； 相對散射干擾，隨機干擾的壓制效果則較差，部分有效信號仍淹沒于干擾中。對比延時加權組合與F-K濾波的頻譜(圖7)，可見二者頻帶特征與原始資料基本一致，都能較好地保持頻率信息； 同時，二者的AVO畸變(圖8)也都較小。

綜合考慮噪聲壓制能力、頻帶保持能力、AVO曲線畸變影響程度等，認為延時加權組合是一種較好的室內組合接收方案。

3 實際數據分析

采用四川某地實際采集地震記錄進一步做室內組合試驗分析。原始記錄雖已做過現場一次靜校正、初至切除、去除異常強振幅噪聲等處理(圖9a)，但仍存在隨機干擾、線性干擾、面波等成分，有效反射在中遠道欠連續，其能量與噪聲背景相近，給后期識別造成一定困擾。

選取相鄰7道(N=7)分別進行常規組合(圖9b)和延時加權組合(圖9c)處理，可見組合處理后隨機噪聲都得到較徹底壓制，反射軸從背景噪聲中凸顯出來。但另一方面，常規組合在中遠道對有效波損傷較大； 而延時加權組合則考慮到了傳播時差，對有效反射能做到同相疊加，因此增強了連續性，保護效果更好。從其F-K濾波結果(圖9d)可見，線性干擾及面波得到較好壓制，但隨機噪聲的壓制效果不甚理想，有效反射未能得到相對充分的凸顯。

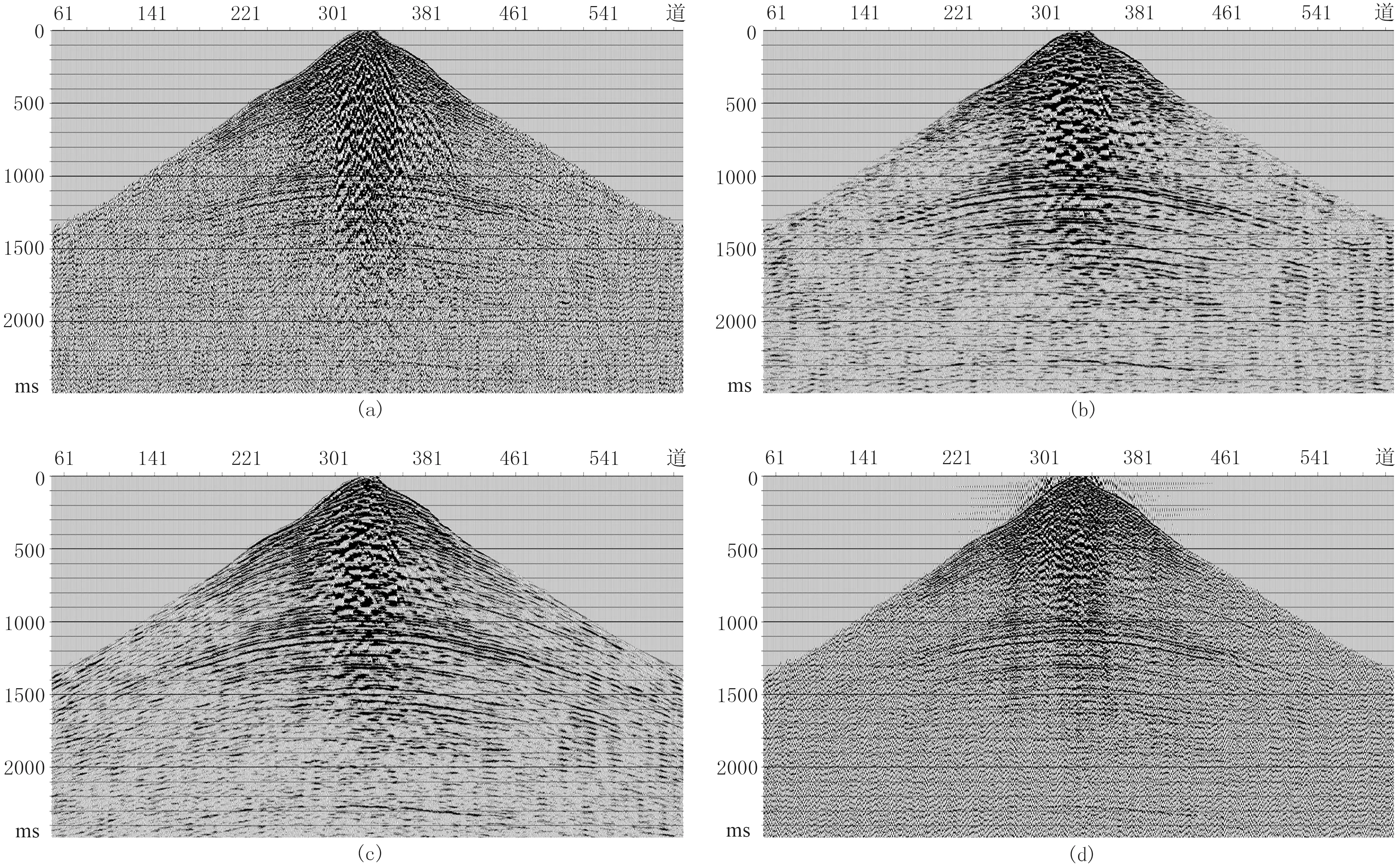
圖9 實際地震記錄組合處理結果

4 討論與結論

組內距、組合個數、加權系數、延時量、輸入子波頻率成分等，都會影響組合輸出的空間能量響應形態。根據有效信號和噪聲在入射角度上的差異，可將空間劃分為指向目的層的有效反射部分和近地表的潛在噪聲部分，這兩部分的能量比值構成了理論信噪比。

使理論信噪比達到最大，就是組合參數優化設計的目標和結果。常規組合一般只考慮檢波器組合個數和組內距兩參數，試驗表明這種組合方式對噪聲干擾壓制較好，但對反射振幅也有一定程度損害，且造成主頻降低。延時等權組合將延時量加入目標函數，控制接收相位差使反射波能量同相疊加，從而保證了主頻與原始資料接近，減輕了對反射振幅的損害，但也增強了與有效波方向近似的干擾波能量。延時加權組合綜合考慮了檢波器組合數目、組內距、延時量和加權系數等因素，在保證反射波振幅同相疊加的同時，通過加權系數能進一步調整組合方向因子形態，進而壓制干擾，整體上提高了地震記錄信噪比。

對比延時加權組合與F-K濾波的效果得知，二者在壓制規則干擾和頻帶保持方面都有較好表現，但F-K濾波對隨機噪聲壓制能力不足，而這恰好是組合類方法的優勢。因此，應用延時加權組合手段壓制噪聲具有良好應用前景。