基于神經網絡的車輛抗沖擊防護組件優化*

李明星，王顯會，周云波，孫曉旺，曾 斌，胡文海

（1. 南京理工大學機械工程學院，江蘇 南京 210094；2. 東風汽車公司技術中心，湖北 武漢 430056）

在目前反恐戰爭和未來武裝沖突中，軍用高機動車輛面臨主要威脅形態為非對稱威脅，其中最具代表性的是地雷簡易爆炸裝置（improvised explosive device, IED）[1]，提供可以對付IED 威脅的輕型高機動車輛成為部隊的最新需求。如何提高軍用高機動車輛防護能力以保障車內乘員安全，已經成為多學科交叉前沿研究課題[2]，目前主要采用V 型結構來提高軍用車輛底部抗爆炸能力。而防護組件的設計需要根據具體車型的特性來匹配，同時隨著防護要求的不斷提高，防護組件的設計面臨越來越多的挑戰。

Kendale 等[3]結合實驗和仿真分析，對不同的車體形狀下乘員的損傷進行研究。結果表明，底部為V 型結構的車體具有偏置爆炸沖擊波的作用，能夠有效減小爆炸沖擊作用力，從而降低乘員損傷風險。張中英等[4]在兼顧其通過性與防護能力時，通過仿真分析研究得出V 型角度取值為140°最合適。不過V 型車身底部結構的最大不足之處是車身的離地距離較大，使得車輛的操縱性降低。目前國內發展較快的軍用高機動車輛，其防護組件的選取很少直接采用V 型底部結構。含蜂窩夾層的V 型底部復合裝甲是近幾年的研究成果，不僅存在V 型結構偏置爆炸沖擊能量，而且裝甲內部的蜂窩組件還存在一定的吸能作用。孫京帥[5]分析了在面內沖擊載荷作用下，蜂窩材料變形機制與其相應的能量吸收性能，并分析了蜂窩單元幾何尺寸對蜂窩吸能、質量及比吸能的影響。目前相關學者對防護組件性能的研究多局限于對其某個特性進行分析改進，對防護組件的整體設計進行分析研究的相對較少。

針對目前對防護組件設計研究的局限性，本文中對防護組件整體性能優化進行了大量的仿真分析工作與實驗驗證。傳統的防護組件設計需要通過大量的實驗與有限元仿真的配合，有經驗的工程師也需要通過大量的計算先獲得仿真結果較好的模型后，再通過實驗驗證最終確定設計方案。近年來，隨著優化理論的發展，神經網絡和遺傳算法在結構優化設計中得到越來越廣泛的應用。Feng[6]提出一種基于粒子群優化的RBF 神經網絡優化算法，可以提高整個神經網絡的性能。柳建容等[7]基于神經網絡遺傳算法對減震器進行仿真分析，獲得了較好的優化結果。本文中以實驗為基礎，結合有限元分析得到的數據，同時利用神經網絡和遺傳算法對防護組件進行優化設計。

1 抗沖擊組件爆炸模擬與實驗

1.1 抗沖擊組件模型描述

基于某型車的防護組件初步設計方案如圖1 所示。防護組件整體采用螺栓連接，其面板與背板之間填充蜂窩鋁，兩側有限位鋼板。此時防護組件面板背板厚度均為6 mm，板內橫梁厚度為4 mm。防護組件長1 800 mm、寬1 500 mm。防護組件面板距地面450 mm。梁采用BS700 鋼，面板及背板采用6252 裝甲鋼。

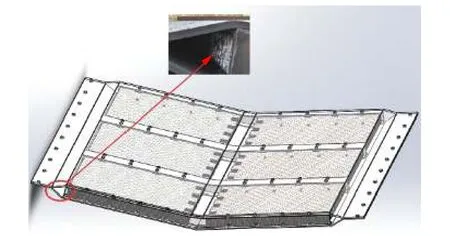
圖1 防護組件結構圖Fig. 1 Structure of protective component

1.2 抗沖擊組件爆炸仿真理論

有限元模型如圖2 所示，為確保仿真與實驗模型的一致性，在配重塊上增加了質量單元對整個模型進行配重處理，使仿真模型質量與實驗模型質量一致。除此之外，在有限元模型中還建立了空氣、土壤和炸藥模型。裝甲材料為高強鋼，在有限元中采用LS-DYNA 中3 號材料模型*MAT_PLASTIC_KINEMATIC：

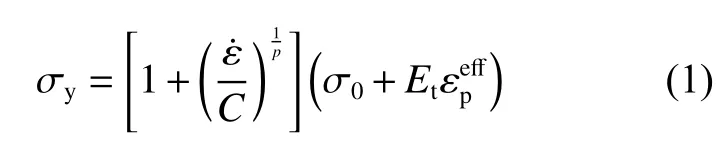
式中：σy為初始屈服極限，Et為硬化模量，為應變率，C 和p 為應變率參數。LS-DYNA 中包含高能燃燒模型（CJ）和點火生成模型（ZND），因為ZND 模型的炸藥參數缺少實驗支撐，所以仿真中一般使用CJ 模型。CJ 模型中的Jones-Wilkins-Lee（JWL）方程是半經驗狀態方程，其壓力、體積和內能之間的關系為：

圖2 臺架仿真有限元模型Fig. 2 Bench simulation finite element model

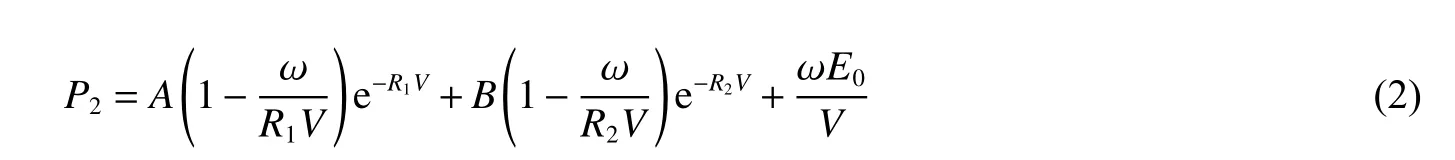
式中：P2為壓力，E0為初始內能密度，為相對體積，A、B、R1、R2、ω 為材料常數，狀態方程中的參數見表1[8]。

表1 TNT 炸藥的JWL 方程參數Table 1 JWL equation parameters of TNT explosives

1.3 抗沖擊組件臺架實驗

實驗時防護組件上方放置一塊平鋼板以模擬整車中的地板變形。將防護組件安裝在臺架上，并用質地均勻的配重塊以整車的質量進行配重實驗。實驗則按AEP-55 標準的2b 等級進行，即將6 kg 當量的TNT 放在防護組件下方任意位置進行爆炸實驗，本次實驗選取具有代表性的正下方進行爆炸驗證。爆炸實驗后上板、中間鋁結構、底板分離，連接螺栓全部斷裂；邊緣及面板均有彎曲變形；中間鋁結構部分被壓潰至極限。爆炸后模擬整車地板的鋼板發生很大程度的彎曲變形，變形量達210 mm，鋼板整體呈上凸狀，鋼板表面出現多處凹坑，其中一側邊緣部分受壓變形，出現裂紋。

由爆炸實驗的結果來看，初步設計的防護組件無法滿足AEP-55 法規的2b 實驗要求。防護組件在6 kg 當量TNT 的爆炸沖擊下解體，模擬整車底板的變形量未能符合小于150 mm 變形量的設計要求。因此需要在此實驗的基礎上對防護組件進行優化，直到其滿足設計要求。圖3 所示為數值仿真與實驗中防護組件的壓潰變形情況。

圖3 數值仿真與實驗中的抗爆組件壓潰情況Fig. 3 The crushing situation of anti-explosion components in numerical simulation and experiment

通過仿真與實驗的對比，可以看出仿真分析與實驗結果有較好的一致性，為后續的仿真分析與優化工作奠定了基礎。產品設計過程需要采用各種優化方法，不能單獨依靠數學規劃的優化手段。由于防雷板組件相對復雜，單純的依賴最優化方法是難以做到的，應結合目前國內外設計經驗盡可能采用V 型結構。鑒于給定的設計空間，該防護組件最大V 型角度能達到160°。在此基礎上通過優化設計改變面板背板材料、改變面板與背板之間梁的布置，以提高防護組件的整體防護性能。

2 抗沖擊組件多響應參數優化

2.1 優化數學模型構建

提高防護組件的整體防雷效果可以通過調整面板、背板和加強梁的相關參數匹配，實現防雷組件整體性能的優化。同時可以通過優化軟件的靈敏度分析，確定各個設計變量中對優化目標效果較明顯的設計因子。在防護組件抗沖擊性能優化設計中，設計變量如圖4 所示，選取5 個尺寸變量、2 個形狀變量，其位置如圖5 所示，初始值及其取值范圍如表2 所示，變量X1～X5為厚度變量，此處對變量X6、X7作簡要說明：在Hypermes 的tool 面板下選擇HyperMorph 工具，對要需要變形的網格進行處理。首先創建變形域，如圖5 所示，然后選擇相應的變形指令，本文中研究中間橫梁在防護組件之間的布局對防護組件整體性能的影響，所以對橫梁的變形操縱為沿x 方向的移動。前后移動量各取200 mm，然后對變形的節點信息輸出節點信息文件，且其變量范圍為操縱時輸出變量數據的百分比。在優化工具Hyperstudy 中通過調用相應節點文件來生成變量。在防護組件結構設計中，防雷板變形位移量D 與防雷板總體質量M 最小化，該優化問題的數學模型為：

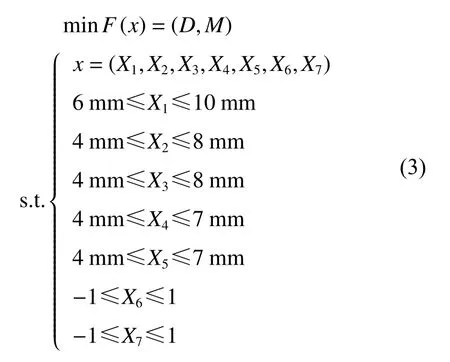
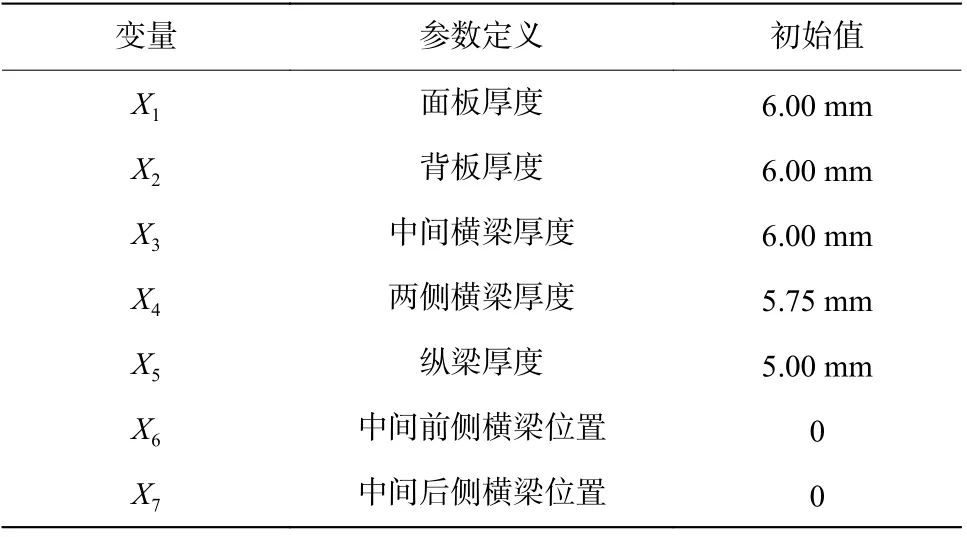
表2 設計變量初始值Table 2 Design variable initial value

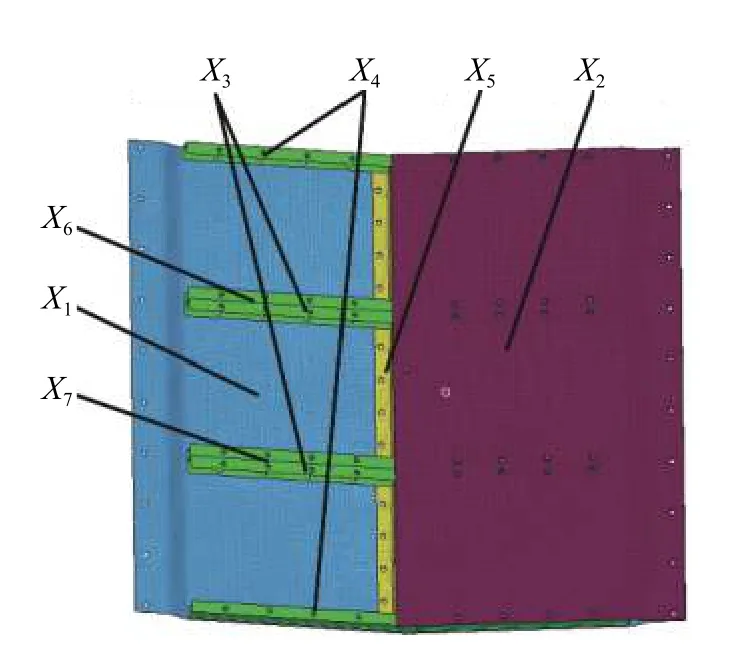
圖4 設計變量位置示意圖Fig. 4 Design variable position diagram

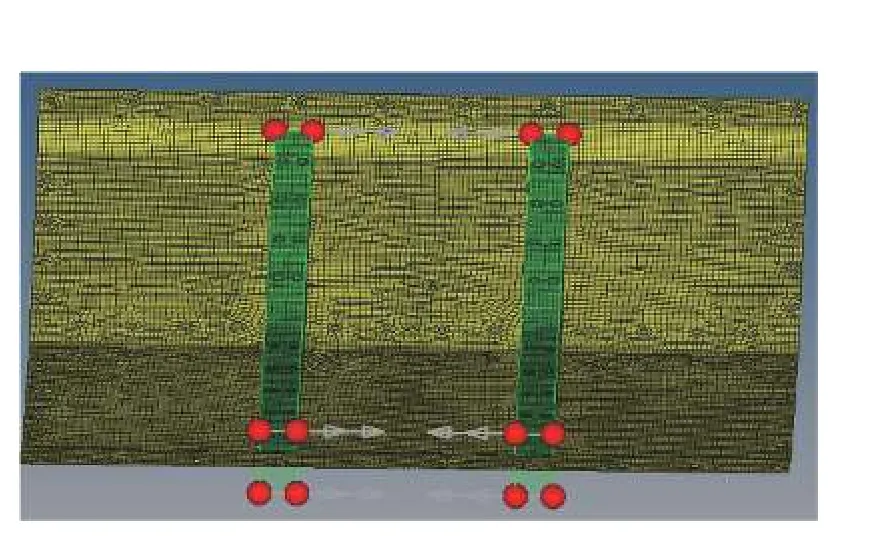
圖5 變形域圖Fig. 5 Deformation domain diagram

2.2 抗沖擊組件參數影響分析

常用的實驗設計方法有：中心組合設計（CCD）、Box-Behnken 設計、拉丁超立方設計等。CCD 應用二次多項式預測其對評價指標的影響，優點為實驗少、設計簡單且有較好的預測能力。Box-Behnken 設計方法具有近似旋轉對稱性，避免了極端點的出現，缺點是該設計方法只能包含3～21 個因子。拉丁超立方實驗設計具有效率高和采用均衡性好等優點[9]。由于研究對象的高度非線性，具有空間隨機填充能力的拉丁超立方實驗設計，較CCD、Box-Behnken 設計具有用同樣的點數可以研究更多組合的優點。為了獲得具有全局意義的神經網絡模型，利用拉丁超立方實驗方法對7 個設計變量進行采點，共有40 組樣本點。樣本的因素及水平情況如表3 所示。

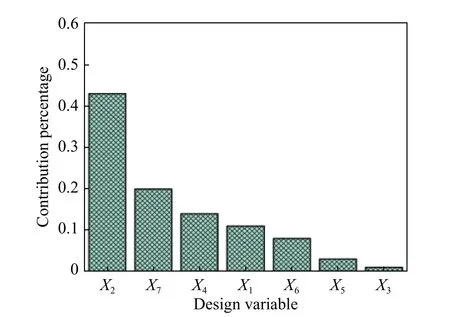
圖6 設計變量貢獻率Fig. 6 Design variable contribution rate

結合方差靈敏度分析[10]（ANOVA）方法分析了7 個設計變量對防護組件變形位移響應量的貢獻率，如圖6 所示，設計目標在滿足質量要求的前提下其防護組件的位移量要盡可能小，所以靈敏度分析只需觀察各設計變量對輸出變量位移量的貢獻量。由分析可知，X3即中間橫梁厚度與X5縱梁厚度對防雷板變形位移量的影響極小，所以在后續數值優化中將剔除這兩個設計變量。

表3 拉丁超立方實驗采樣樣本Table 3 Latin hypercube test sample

2.3 神經網絡響應面構建

將拉丁超立方實驗樣本得到的有限元分析數據用于擬合近似模型。基于近似模型進行的優化設計的優勢在于：將復雜的工程優化問題轉換為數學尋優問題，可以極大地減小工作量。主流近似模型有Kriging 模型、神經網絡模型等。Kriging 以變異函數理論和結構分析為基礎，其某未觀測點表達式為：

式中：λi為待定加權系數。λi應滿足兩個條件：

（1）無偏估計，設估值點的真值為y(x0)。因模型空間的變異性，y(xi)以及和y(x0)可視作隨機變量，即為無偏估計：

式中：γ(xi，xj)表示以xi和xj兩點的距離作為間距h 時參數的半方差值。Kriging 常用的核函數為高斯函數與指數函數。在擬合設計變量多且高非線性的工程問題中，Kriging 模型存在較大誤差。

神經網絡近似模型有徑向基函數（RBF）神經網絡，和橢圓基函數（EBF）神經網絡。將優化變量作為輸入層，響應目標作為輸出層，隱含層由激活函數構建的神經元組成。RBF 神經網絡通常以高斯函數作為激活函數，對任意輸入x 的輸出層中第k 個神經元可以表達為：

徑向基函數神經網絡由于其簡單的拓撲結構和全局逼近能力在信號處理[11]與非線性系統建模和控制等方面得到了廣泛的應用[12]。神經網絡結構優化方法有很多。進化算法是基于生物進化原理的一種搜索算法，有較好的魯棒性與全局搜索能力，湊式法通過訓練與比較不同的RBF 神經網絡結構來實現，但時長較長[13-16]。相對而言進化算法更適合防護組件設計優化的匹配。防護組件的設計變量與其動態響應參數之間是一種高度非線性映射關系，對于復雜系統兩者之間很難用函數關系顯示表達。而神經網絡有極強的非線性映射功能，非常適用于建立這種復雜的非線性模型[17]。圖7 為神經網絡和Kriging模型擬合的響應面，可以看出，由于Kriging 采用無偏估計盡可能平滑的接近樣本點，當非線性程度非常高時，擬合存在較大差異。而神經網絡代理模型對于高度非線性問題具有更好的擬合效果。因此本文中采用神經網絡模型作為后續數學優化的基礎。圖8 為主影響因子X2與X1、X4、X6和X7四個因子擬合的位移響應面。

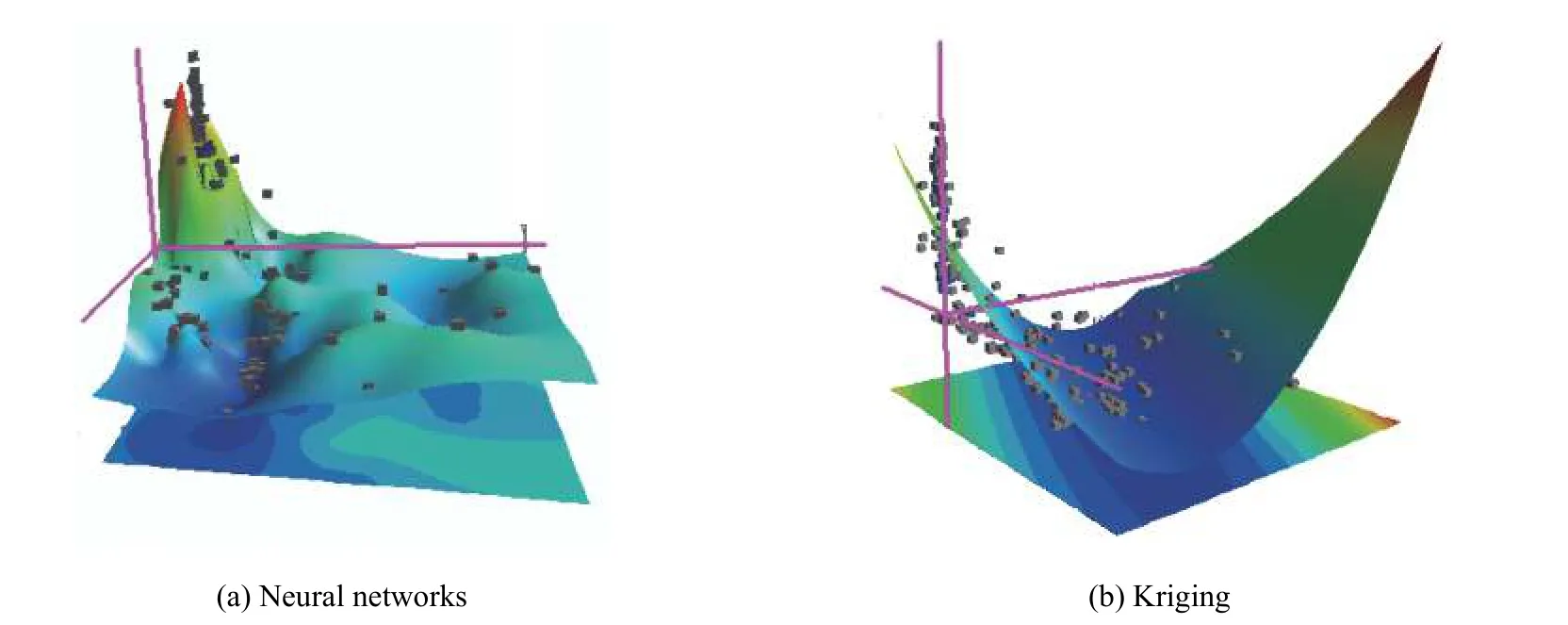
圖7 神經網絡模型與Kriging 模型對比Fig. 7 Comparison between neural network model and Kriging model

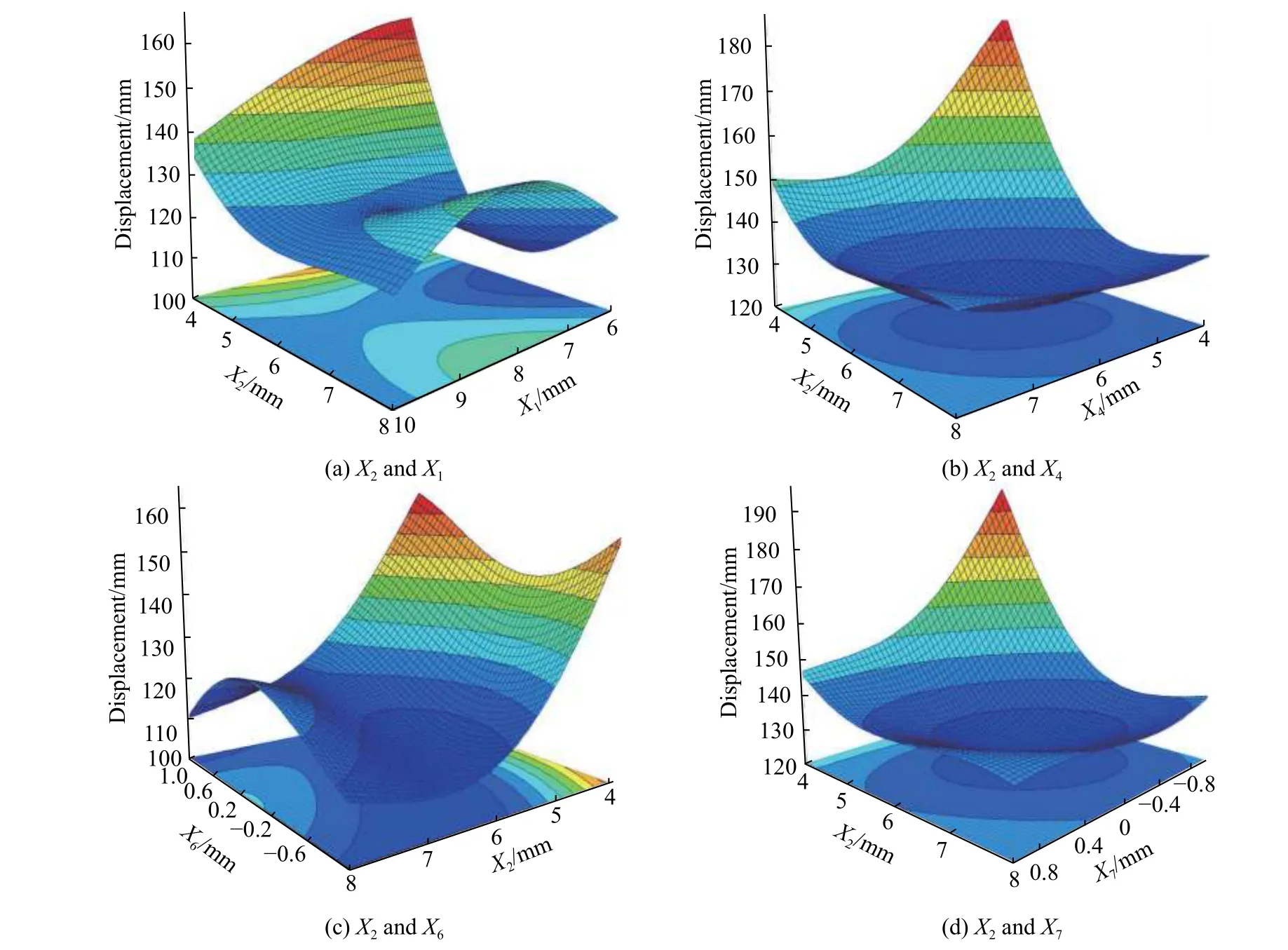
圖8 主影響因子X2 分別與X1、X4、X6 和X7 擬合的位移響應面Fig. 8 Response surfaces of displacements where the main influence factor X2 fits X1, X4, X6 and X7, respectively

3 優化結果分析

3.1 抗沖擊組件的帕累托前沿

利用帕累托原理的尋優算法對已構建的近似模型進行求解，獲得由樣本空間內最佳值構成的帕累托前沿。針對防護組件優化設計問題，主要運用徑向基函數（RBF）神經網絡與多目標遺傳算法(MOGA)進行數值優化，基于帕累托的多目標遺傳算法(MOGA)的核心在于非支配集算法的構成[18]。算法收斂的本質為非支配集不斷接近于實際問題理論的帕累托最優邊界的過程[19]。對防護組件結構的數學模型進行求解，改變數學模型為二維多目標優化問題，通過帕累托解集進行描述。遺傳代數設為200 代，各精英數量占10%，變異率取值0.05，獲得8 000 組解及對應的68 組帕累托解集如圖9 所示，結合工程實際需要對優化結果的尺寸進行修正：X1=6 mm，X2=7.5 mm，X3=6 mm，X4=4.5 mm，X5=5 mm，X6=0.9，X7=-0.5。該優化結果（最優解）是由神經網絡代理模型預測所得，為了驗證優化結果的準確性，需對數值優化結果進行仿真計算與實驗驗證。

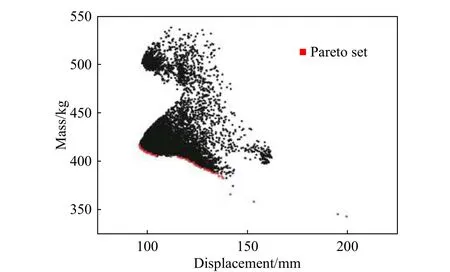
圖9 帕累托最優解集Fig. 9 Pareto optimal solution set

3.2 優化結果實驗驗證

以同樣的邊界條件對優化設計出的防護組件進行實爆實驗，從實驗結果來看，優化后的防護組件可以在6 kg 當量的TNT 爆炸沖擊下保持完整而不破裂。如圖10～12 所示，較初步設計方案其防護性能提升顯著，同時通過仿真分析得到防護組件背板實驗損傷圖。優化后防護組件背板變形量顯著降低。由于背板最低點到背板安裝點的垂向距離為100 mm，所以仿真模擬地板的最大變形量為139 mm，代理模型的數值為134 mm，其相對誤差為3.6%，代理模型相對誤差較小。從表4 可知，優化后模擬地板變形量減小36.2%，防護組件質量增加8.2%。背板塑性變形量為171 mm，實驗后測得背板最大塑性變形量為176 mm，仿真結果與實驗結果相對誤差為2.8%。通過仿真與實驗進一步驗證該優化方案可靠，符合設計要求。

圖10 抗爆組件優化后實驗狀態Fig. 10 Experimental status of anti-explosion components after optimization

圖11 仿真與實驗背板塑性變形圖Fig. 11 Simulation and experimental plastic deformation of the back plate

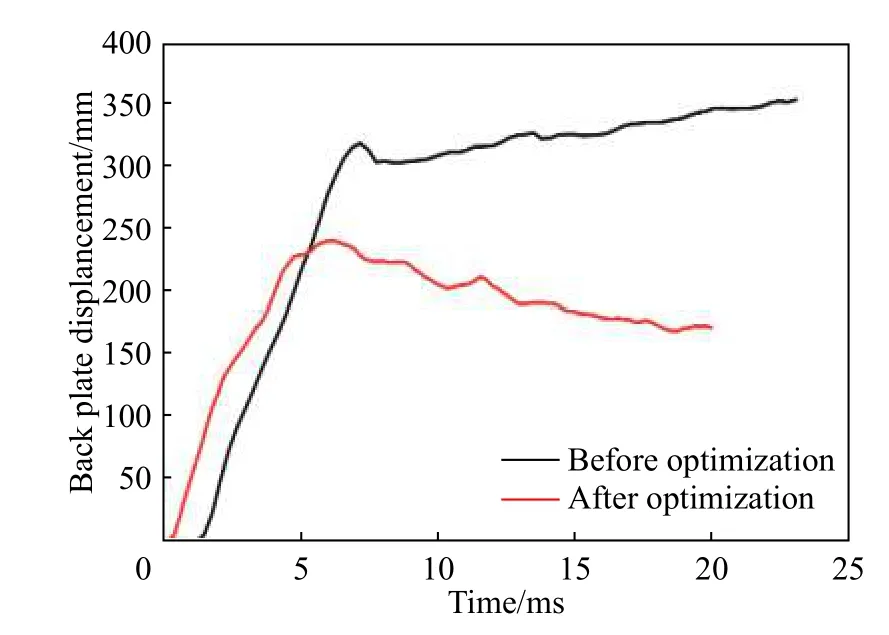
圖12 背板位移曲線Fig. 12 Backplane displacement curves

表4 優化前后對比Table 4 Comparison before and after optimization

4 結 論

基于徑向基函數神經網絡代理模型結合多目標遺傳算法對防護組件進行了優化設計，通過仿真分析、參數篩選，建立了該結構優化設計的準確的代理模型，在神經網絡模型的基礎上通過多目標遺傳算法得到了帕累托最優解集，根據工程需求確定了防護組件的設計參數，并對其進行了仿真驗證與實驗驗證，得到以下結論：

（1）通過參數靈敏度分析可知，背板厚度和面板與背板之間的橫梁布置對防護組件防護性能的影響較大；

（2）通過神經網絡代理模型結合多目標遺傳算法對防護組件結構進行數值優化，提出了防護組件的最優設計方案，可以顯著提升防雷板的防護能力；

（3）對于高度非線性工程問題，神經網絡模型具有較高的擬合精度，對于工程優化設計問題具有很好的應用價值。