數學歸納法的應用與建議

紀定春 蔣紅珠 王若飛

(1.四川省成都師范大學數學科學學院 610068；2.廣東省廣州市華南師范大學數學科學學院 510631)

一、數學歸納法的發展及簡介

數學歸納法是一種基本的數學證明方法，主要用于證明與正整數有關的一些數學命題，它是溝通特殊到一般、有限到無限的橋梁.數學歸納法的思想起源于畢達哥拉斯時代，從特殊的點子數出發，歸納出一般結論.歐幾里得對素數有無窮的證明過程，充分地體現了數學歸納法中歸納遞推的思想.13世紀末，法國數學家萊維·本·熱爾松在證明排列組合問題時，用了現代意義下數學歸納法中的歸納奠基和歸納推理的思想，這標志數學歸納法逐漸走向成熟.帕斯卡在證明帕斯卡三角時，明確運用了現代意義上的數學歸納法的兩個核心步驟，即歸納奠基和歸納推理兩個步驟，這意味著數學歸納法證明的正式確立.意大利數學家皮亞諾發表了《算術原理新方法》，建立了自然數五條公理，數學歸納法有了理論依據，標志著數學歸納法走向成熟.隨后，數學歸納法呈現多樣化的發展，形成了不同類型的歸納法，如第二數學歸納法、蹺蹺板歸納法、倒推歸納法、跳躍歸納法、累積歸納法、無窮歸納法、區間歸納法等.接下來將介紹第一數學歸納法(以下均簡稱：數學歸納法)及其應用.

數學歸納法：

假設命題P(n)是關于正整數n的命題，如果P(n)滿足：(1)命題P(1)為真.(2)假設命題P(k)為真，證明命題P(k+1)為真.由命題(1)、(2)為真，則對正整數n，都有命題P(n)成立.

驗證命題P(1)為真，稱為歸納奠基；通過假設命題題P(k)為真，證明命題P(k+1)為真，稱為歸納遞推(歸納推理)；最后步驟為下結論.

二、數學歸納法的應用

1.求證數列通項中的應用

例1(2014年廣東高考數學卷)設數列{an}的前面的n項和為Sn，關系為Sn=2nan+1-3n2-4n，n∈N*，且S3=15.(1)求a1，a2，a3的值；(2)求數列{an}的通項公式.

解析對問題(1)，由于數列Sn，滿足Sn=2nan+1-3n2-4n.容易得a1=3，a2=5，a3=7.

對問題(2)，由問題(1)中a1，a2，a3值，猜數列{an}通項為：an=2n+1.

現在用數學歸納法來證明以上的猜想.

(1)當n=1時，顯然結論成立.

(2)假設當n=k時結論成立，即ak=2k+1，前k項和為Sk=3+5+…+(2k+1)=k(k+2).

由數列Sk滿足Sk=2kak+1-3k2-4k.

則k(k+2)=2kak+1-3k2-4k，整理可得ak+1=2k+3.

即ak+1=2(k+1)+1，所以當n=k+1時成立.

由(1)和(2)，對任意的n∈N*，有an=2n+1.

故數列{an}通項為an=2n+1.

評注該試題的第二個問題，巧用問題(1)的結果，先猜測出數列的通項相公式，然后再證明猜想，充分體現了“先猜后證”的思維模式，在數學史上很多數學結論的發現，往往就是建立在已有的知識基礎上，利用先猜想后證明的方式進行的.

2.證明不等式中的應用

例2(2019年浙江高考數學卷第20題)設等差數列{an}的前n項和為Sn，a3=4，a4=S3，數列{bn}滿足：對每個n∈N*，Sn+bn，Sn+1+bn，Sn+2+bn成等比數列.

(1)求數列{an}，{bn}的通項公式；

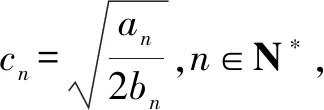
解析問題(1)，解答過程略.利用等差數列和等比數列的知識點及上述的關系式可得，數列an=2n-2，bn=n2+n，其中n∈N*.

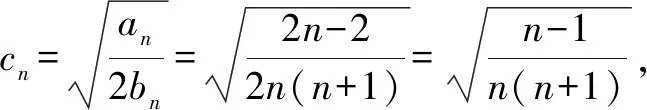
顯然這個不等式是關于正整數n的命題，考慮用數學歸納法證明.

(1)當n=1時，有c1=0<2，顯然不等式成立.

即當n=k+1時，不等式成立.

評注該試題從直接法不容易解決，又注意到需要求證的命題為一個關于正整數n的命題，自然想到使用數學歸納法.

例3(2014安徽高考數學理科卷第21題)設c>0，整數p>1，p∈N*.(1)證明：當x>-1且x≠0時，有(1+x)p>1+px；(2)略.

BP神經網絡是目前應用最廣泛的神經網絡，是一種復雜的非線性映射系統，能以任意精度逼近，削弱坐標轉換中的系統誤差與異常誤差等因素的影響。但該方法具有容易陷入局部極小值、外推能力差等缺點，因此，還需要研究改進神經網絡學習算法，進一步提高該方法在坐標轉換中的精度與可靠性。

證明問題(1)是關于正整數p的命題，考慮使用數學歸納法.①當p=2時，有(1+x)2=1+2x+x2.當x>-1且x≠0，有x2>0，故(1+x)2>1+2x成立.②假設當p=k(k≥2)時，命題(1+x)k>1+kx成立.由假設可得(1+x)k+1=(1+x)k(1+x)>(1+kx)(1+x)=1+(k+1)x+kx2.因為kx2>0，所以(1+x)k+1>1+(k+1)x.故當p=k+1時命題成立.

由①和②知，對于任意的整數p>1，p∈N*，當x>-1且x≠0時，有不等式(1+x)p>1+px成立.

評注該試題的解法除了數學歸納法之外還有其它方法，如二項式展開、伯努利不等式.解決該問題的關鍵在于巧用“(1+x)k+1”的變形，然后根據假設的不等式進行放縮.

3.證明整除性中的應用

例4證明：當n∈N*時，11n+2+122n+1能夠被133整除.

證明這是一個關于正整數n的整除性命題問題，考慮使用數學歸納法.

(1)當n=1時，11n+2+122n+1=113+123=(11+12)(112-11·12+122)=23×133.則當n=1時，能被133整除.

(2)假設當n=k時，11k+2+122k+1能夠被133整除.

當n=k+1時，有11n+2+122n+1=11k+3+122k+3，采用“配湊法”變形可得11k+3+122k+3=133×122k+1+11×(11k+2+122k+1).

其中133×122k+1能夠被133整除.

由假設可知11k+2+122k+1能夠被133整除，故11×(11k+2+122k+1)被133整除.

因此當n=k+1時，11n+2+122n+1=11k+3+122k+3能被133整除.

由(1)和(2)可知，對任意的n∈N*，11n+2+122n+1能被133整除.

評注解決該整除性命題的關鍵在于巧妙運用“配湊法”，將“11k+3+122k+3”與“11k+2+122k+1”建立聯系，再由假設可以證當n=k+1時命題成立.

4.證明恒等式中的應用

故當n=k+1時，等式成立.

評注該試題的思路可以歸結為：觀察→試算→猜想→驗證(證明).這一步的推理過程是需要進行嚴密的邏輯推理的.經過了觀察、試算、猜想，并不能夠說明猜想的結果是正確的，這時需要用數學歸納法進行驗證.

三、建議

在最近的幾次課程改革中，數學歸納法一直不被重視，以前高考要考，老師要教，現在的高考數學對數學歸納法已經不作要求，很多高中老師已不講，甚至不提數學歸納法，顯然是對數學歸納法的重要性認識還不夠，也是對人類智慧結晶的損失.數學歸納法是一種重要的數學證明方法，建議將數學歸納法的內容納入高中數學必修內容.原因如下，其一，數學家龐加萊和華羅庚先生都十分地推崇數學歸納法；其二，數學歸納法作為人類智慧的結晶，是在歷經了千年的發展中逐漸成熟和豐富的，是人類從有限證明向無限證明的飛躍，是人類認識無限的光輝范例；其三，數學歸納法是發展的，具有強勁的生長力，通過數學歸納法可以派生出很多其它類型的歸納法，因此可以認為數學歸納法是其它歸納法的“母本”；其四，高等數學中常常用數學歸納法來證明關于自然數的無限命題，以《高等代數(第四版)》(北大數學系前代數小組編)為例，使用數學歸納法證明定理、例題(不含課后習題)高達18次，足見數學歸納法在高等數學中的重要地位；其五，發達國家對數學歸納法的要求較高，且普遍高于我國的要求，如日本、美國等.其六，數學歸納法蘊含豐富的文化內涵，是文化育人的好素材.最后，數學歸納法在高中階段是可教的、可學的，有很多優秀的教學案例可以幫助教師的教和學生的學習.因此，建議在下一次修訂高中數學課程標準時，將數學歸納法納入必修內容.