考慮滲流影響的基坑變形規律與穩定性研究

何 應 道

(1.中鐵第四勘察設計院集團有限公司， 湖北 武漢 430071； 2.水下隧道技術國家地方聯合工程研究中心， 湖北 武漢 430071)

近年來,眾多的跨海大橋、深水筑港、大型地鐵隧道等工程的建造使中國已經成為了舉世聞名的交通大國，我國在沿江、近海等地下水豐富的地區大量修建了穿江過海的公路或地鐵等戰略性、基礎性工程，而這些工程往往需要在高水壓、強滲透地層中開挖修建深基坑，會對天然土層的應力場與滲流場造成巨大影響[1-3]，使得滲流作用對基坑變形與穩定性影響的研究成為目前工程設計與施工中的難點問題。

國內外在深基坑變形方面研究較多，Ou等[4]采用有限元法進行不排水分析和排水分析研究得出，當基坑工程開挖周期較長時，排水分析較為符合實際情況。Richard等[5]采用數值模擬方法研究得出了粘性土層基坑的各項變形規律特征。劉歷波等[6]在進行數值模擬分析考慮地下水的滲流作用得出的深基坑的各項變形模擬結果與監測結果較為吻合。張小偉等[7]通過有限元ABAQUS研究軟土地區深基坑的變形情況，研究表明滲流對基坑變形的影響不容忽視。李體康[8]基于滲流應力耦合理論和修正劍橋模型(MCC)，結合某工程算例分析了基坑周邊的滲流場變化和基坑各項變形，發現沒有考慮滲流作用的結果偏于不安全，而考慮滲流合作用能較為準確反映基坑滲流與變形情況。目前，我國對基坑開挖時的滲流場變化和變形情況大都依賴傳統簡化的經驗公式[9-11]，對于復雜地質下的工況很難進行更準確的計算，因而漸漸不能滿足日益提高的工程要求。柳治富等[12]從土的組成和水動力條件兩方面來評價武漢長江隧道工程基坑土體的滲透穩定性，且進一步提出了抵御基坑土體滲透變形的方法和應對措施。曾锃等[13]以某水庫大壩反濾層的滲透穩定性研究為例嘗試了一種用傳統滲流理論確定工程體滲透穩定的薄弱部位，用顆粒分析方法研究其滲透穩定性的新方法。

總的來說，國內外的基坑設計規范考慮滲流影響的不多，而在強滲透地層中，滲流對基坑變形的影響[14-16]不容忽視。而我國現階段對于強滲透地層的基坑研究還較少，對于強滲透地層中滲流作用的影響與規律還缺乏深入的研究與認識，本文以常德沅江隧道江北明挖暗埋段基坑工程為研究對象，利用流固耦合數值模擬方法，研究不同的土層滲透系數對深基坑變形和基坑底部滲流穩定的影響，得到了一些有益的結論，本研究在工程中具有重要意義和先進性。

1 工程背景及計算模型

1.1 工程背景

常德沅江隧道明挖段基坑根據結構型式的不同可分為敞開段、暗埋段及工作井3部分，基坑總長約560 m(江南明挖段總長290 m，江北總長270 m)，基坑開挖深度1.3 m～21 m，基坑寬度為：敞開段約22 m，暗埋段約28 m～35 m，工作井寬34 m～36 m。其中，含水圓礫層透水性強，滲透系數最大可達6×10-4m/s，且距離沅江較近，基坑側壁涌水量很大。沅江隧道江北里程YK0+270—YK0+370段為明挖暗埋段，考慮到基坑計算的典型性，在本次研究中選取降水開挖施工段YK0+336—YK0+370為研究對象，深度約12 m。其場地上部雜填土厚在4 m左右，粉土層厚在4 m左右，其下圓礫層厚超過80 m左右，其間粉細砂夾層厚在8 m左右。

1.2 計算模型

采用有限差分軟件FLAC3D建立基坑模型，如圖1所示，基坑長度(x軸)為29 m，寬(y軸)14 m，z方向為地連墻嵌入深度方向，地連墻厚度為1 m，實際計算中為簡化問題，利用對稱性只建立四分之一的基坑模型。地連墻和內支撐采用線彈性模型，土體采用摩爾-庫侖模型，基坑各土層物理力學參數如表1所示。監測布置如圖1所示，C1—C16為基坑墻后地表沉降監測點，L1—L14為基坑隆起豎向位移監測點，Y1—Y35為地連墻側向位移監測點。土體的滲透系數是影響滲流作用大小最重要的因素之一，而基坑底板以下的深厚圓礫層屬于強滲透地層，滲透系數達到6×10-4m/s，為了研究強滲透地層滲透性質對滲流作用的影響，本文以圓礫層的滲透系數為基準值，取該基準值的0.5倍(3×10-4m/s)、2倍(12×10-4m/s)分別進行對比分析。

表1 土層物理力學參數

圖1 監測點布置示意圖

2 結果分析

本次計算結果見圖2—圖4、表2。圖2為三種不同土體滲透系數的深基坑開挖完成后的基坑底部隆起曲線。可以發現三種情況下基坑底部隆起變形規律是基本一致的，測點在地連墻處基坑隆起量最小，距連續墻1 m處隆起量顯著上升，三種不同土體滲透系數的基坑底部隆起量均在基坑中心處最大。當土體的滲透系數為12×10-4m/s時，最大值為184.08 mm，而當土體的滲透系數為6×10-4m/s和3×10-4m/s時，二者的基坑底部隆起量近乎相等，最大值分別為88.45 mm和85.34 mm，前者的基坑底部隆起量約等于后兩者的2倍。說明當滲透系數減小時，基坑底部的隆起值會隨之減小，且變化量較大，但當土體滲透系數繼續減小到一定值時，則對基坑底部的隆起變形幾乎沒有影響。

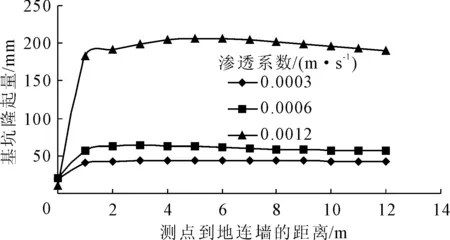
圖2 土體不同滲透系數下的基坑底部隆起量

由圖3可見，不同滲透系數的墻后地表沉降曲線的整體變化趨勢是一致的，皆呈勺子狀，最大沉降均在基坑外17 m至22 m左右，距地下連續墻約34 m后基坑開挖對墻后地表沉降幾乎沒有影響。隨滲透系數增大，其最大沉降值約為62.25 mm、81.46 mm和85.58 mm，量值相差并不明顯。

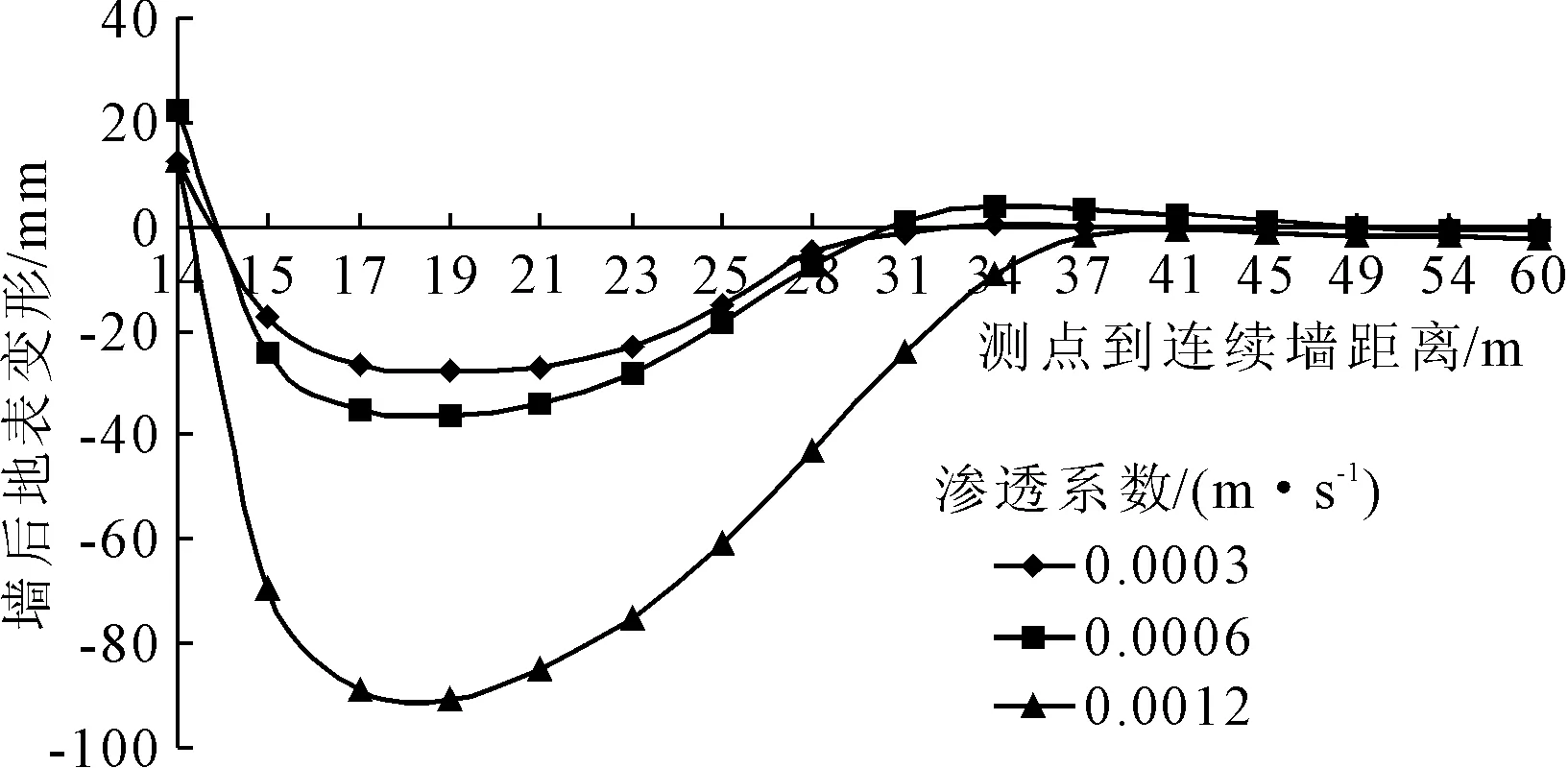
圖3 土體不同滲透系數下的坑外地表沉降

圖4為不同滲透系數條件下的地下連續墻水平位移變化曲線。根據圖4的曲線變化趨勢，可以發現當滲透系數為12×10-4m/s時，連續墻水平位移最大值為95.38 mm，而當滲透系數為6×10-4m/s時，連續墻水平位移最大值為92.23 mm，而當滲透系數為3×10-4m/s時，連續墻水平位移最大值為82.95 mm。總之，隨著土體的滲透系數增大，其水平位移隨之增大，但變化量不大。

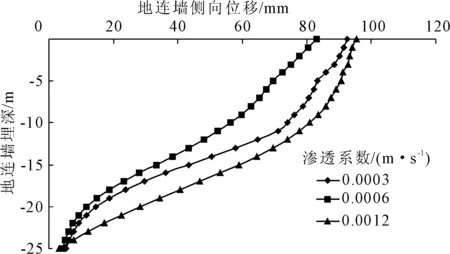
圖4 土體不同滲透系數下的地連墻水平方向側向位移

表2 數值模擬最大值和監測最大值對比

表2列出了滲透系數6×10-4m/s時基坑各項變形的數值模擬最大值和相應部位的監測值，通過對比可知，考慮滲流作用的基坑變形數值結果與實際的監測值比較吻合，說明本文建立的數值模型與采用的計算參數是基本合理的，可以適用于強滲透地層的流固耦合計算。通過對基坑變形結果的分析，可以發現隨著土體滲透系數的增大，基坑降水開挖所引起的地連墻水平位移、墻后地表沉降和基坑底部隆起值均有所增加。且滲透系數的變化對基坑底部隆起的影響較大，對墻后地表沉降和地連墻水平位移的影響較小，當滲透系數達到某一閾值之后，基坑底部隆起量陡升，量值相差較大，原因可能是由于高水壓直接作用于基坑底板處的強滲透圓礫地層，隨滲透性增大，圓礫層發生了由穩定滲流到非穩定滲流的質變。

到現在為止，相關國家基坑規范和手冊[17]大都是假定穩定滲流條件下來評價基坑底部抗滲流能力的強弱，規范中指出，基坑滲流的臨界水力坡降與實際水力坡降之比應大于工程所規定的安全系數，如式(1)所示：

m≤icr/i

(1)

式中：m為基坑底部抗滲流能力的安全系數；i為實際水力坡降；icr為臨界水力坡降，icr=γ′/γω，γ′為土體浮重度；γω為地下水的重度1.0×104N/m3。

根據式(1)，圖5給出了不同滲透系數條件下的基坑底部安全系數變化曲線。如圖5所示，當考慮滲流作用時，圓礫層的滲透系數越大，基坑底部安全系數呈十分明顯的下降趨勢；當不考慮滲流作用時，基坑底部安全系數隨滲透系數的變化趨勢較為平緩。相對而言，基坑底部中心處的安全系數均大于基坑底部坑角處的安全系數，在實際工程中，基坑底部坑角處的滲流穩定問題應更加引起重視。

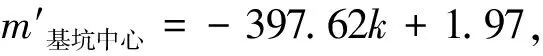
不考慮滲流作用影響時，二者之間的關系分別為：m基坑中心=-73.81k+1.94，m基坑坑角=-83.83k+1.92。

根據數學方法可擬合考慮滲流作用時基坑底部處的安全系數與規范中不考慮滲流作用時基坑底部處的安全系數之間的函數關系為：m′=5.38m-8.48。

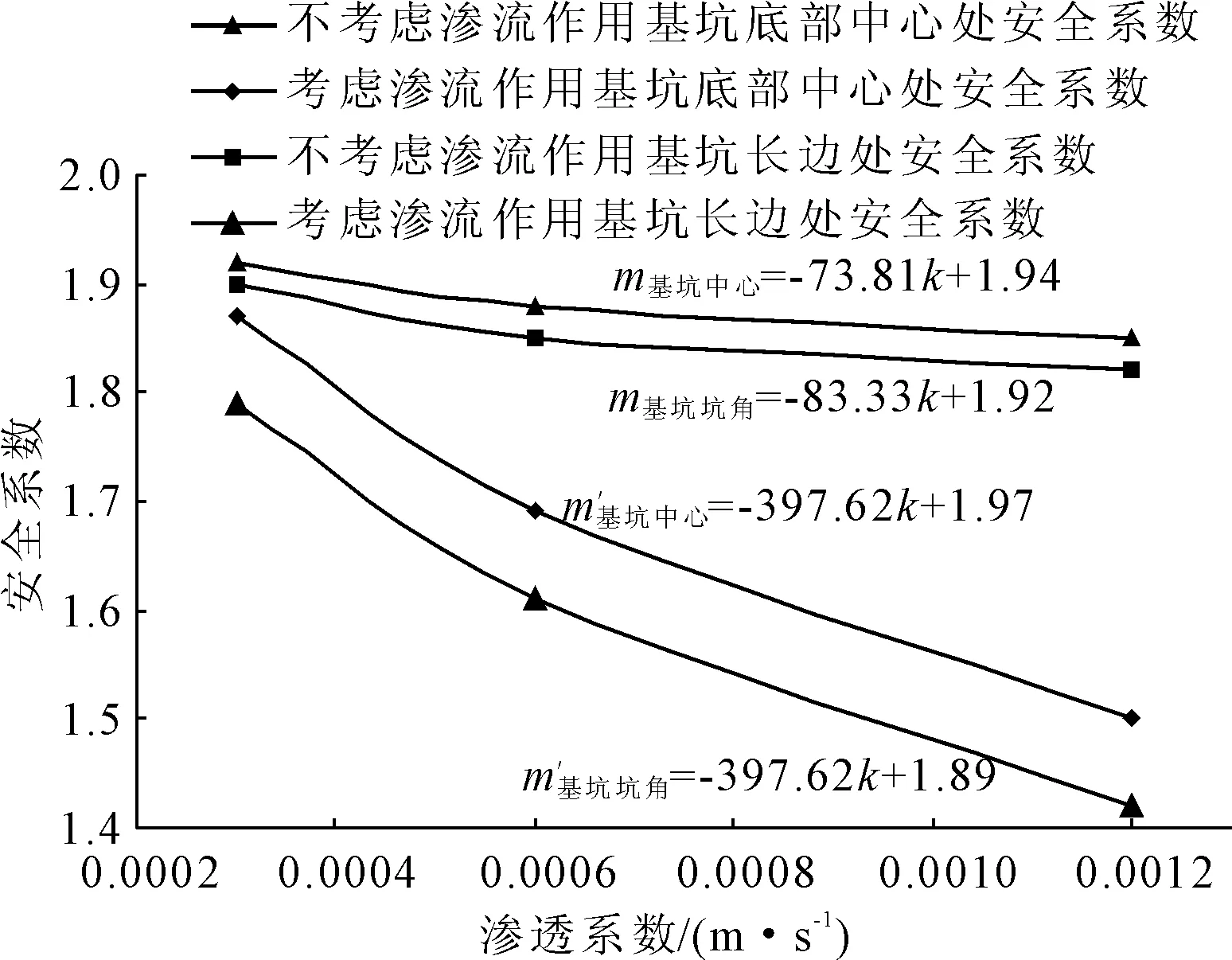
圖5 土體不同滲透系數下的基坑開挖后基坑底部的安全系數

3 結 論

(1) 當考慮滲流作用時，基坑各項變形的模擬計算數值與實際工程的監測結果十分相近，說明本文建立的數值模型與采用的計算參數是基本合理的，可以適用于強滲透地層的流固耦合計算。

(2) 考慮滲流作用時，圓礫層的滲透系數越大，基坑底板安全系數呈十分明顯的下降趨勢；當不考慮滲流作用時，基坑底部安全系數隨滲透系數的變化趨勢較為平緩。