幾何中的動點問題之最值問題

幾何圖形的知識一直是學生學習的難點，它的特點是空間想象力和抽象思維的能力體現，而動點問題就要求更高，本文拿幾何動點最值計算問題為例來說明如何解決這類題型。為解決有關運動問題的最值計算，通常需用到兩種基本模型和一個基本原理：

模型一 點在直線上運動，如下圖，點P 在直線l 上運動，則直線外定點A 與點P 的最小距離為AP 1 時AP 的長最小（即垂線段最短）；

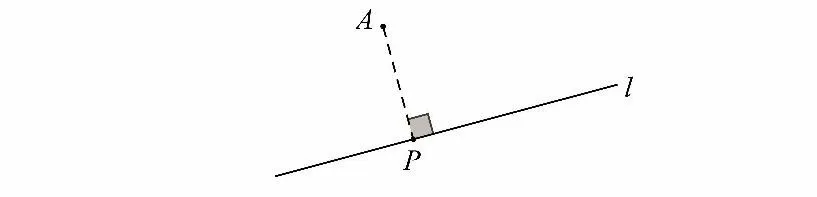
基本原理 當點P 跟隨另一點A 運動而運動時，我們把點A 叫作主動點，點P 叫作從動點.若主動點A 在某一直線l 上運動，則從動點P 也在直線上運動（可能是直線l 也可能是直線m）；若主動點A 在圓上運動，則從動點P 也在圓上運動。

掌握以上兩個基本模型及原理，可以快速有效地解決有關運動為背景的最大（小）值問題。

例1 如圖1-1，等邊三角形ABC 的邊長為4，點D 在AC 邊上運動，以BD為斜邊在BD 上方作含30°角的直角三角形BDE，連接AE，則AE 的最小值為_________。

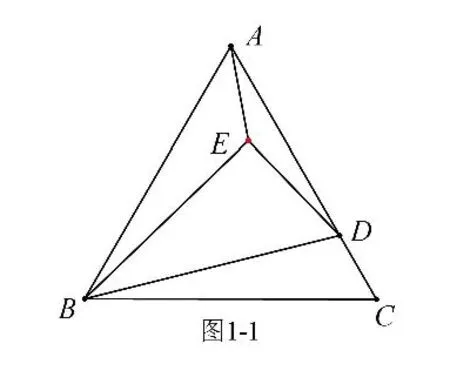
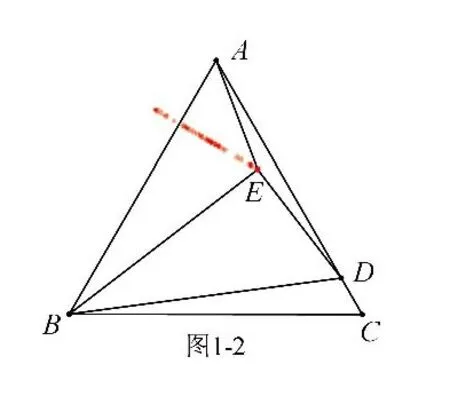
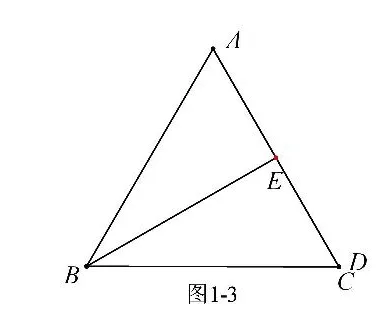
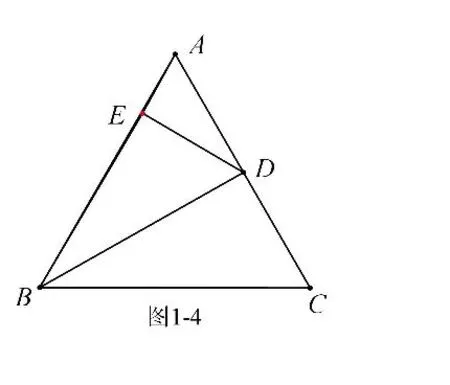
解析：①點E 隨著點D 的運動而運動,點D 在AC 邊上運動（在直線上運動），故點E 也在直線上運動，如圖1-2；②AE 的最小值就是當AE 與直線垂直時的長，點E 運動軌跡（直線）在哪呢（如何確定）？應找兩個特殊點來確定——當D 與C 重合時，E為AC 中點（如圖1-3）；當D 在AC中點處時，E 在AB 上（如圖1-4），所以點E 實際就是在圖1-4 中的直線DE 上運動.顯然在Rt

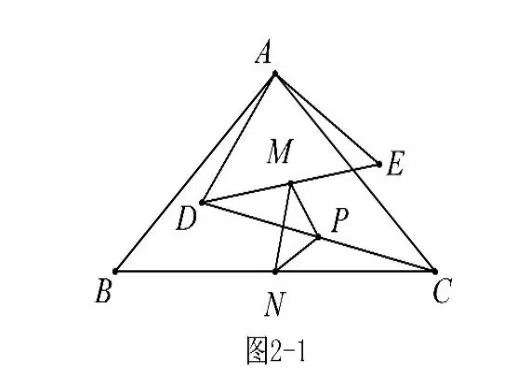
例2 （河南）如圖2-1，在△ABC 與△ADE中，∠BAC=∠DAE=90°,AB=AC=10,AD=AE=4,把△DAE 繞著點A 在平面內自由旋轉，在旋轉過程中，M、P、N 始終分別為DE、CD、BC 的中點，求△PMN 面積的最大值和最小值。

解析：1、在△PMN 中，N是定點，P、M 隨著△ADE 的旋轉而運動，易證△PMN是等腰直角三角形，故△PMN 的面積===即△PMN 的面積隨著邊長的增大而增大；

2、如何求邊長的最大值呢？

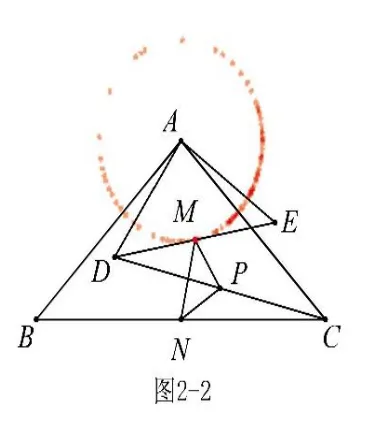
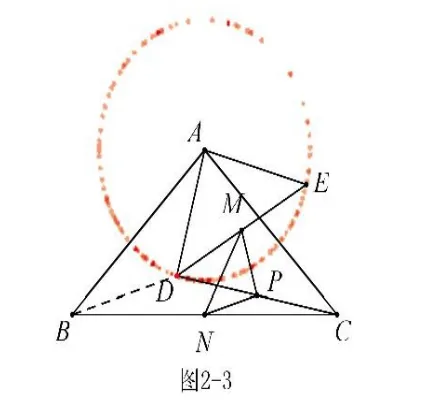
①對于邊長MN，N是定點，M是動點.點M是DE 的中點，AM=，在△ADE 繞點A 旋轉過程中，點M 也繞點A 旋轉（點M 在以A為圓心，為半徑的圓上運動，如圖2-2），顯然MN 最大為，?MN 最小為，?故△PMN 的面積最大為，最小為；②對于邊長PN，N是定點，P是動點，但點P 的運動軌跡無法判斷（圓心不好確定），因此我們必須找到PN 的“親戚”來幫助（自己解決不了的事，就要善于找人代勞，這就是所謂的“轉化”，“不轉化，無數學”），由中位線性質可知，于邊長BD，B是定點，D是動點（顯然點D 在以A為圓心，4為半徑的圓上運動，如圖2-3），因此最大為BDAD=10-4=6，MN 最小為AB-AD=10-4=6，同理可求△PMN 的面積最大為，最小為；③對于邊長PM，可轉化為CE 來解決，不再贅述。

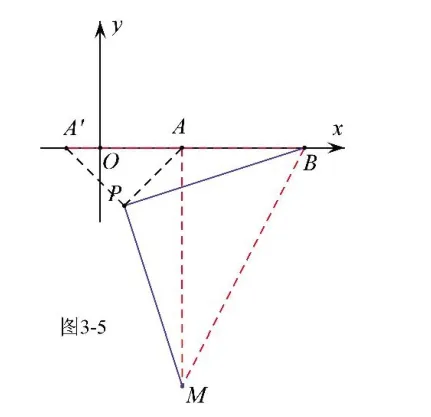
例3 如圖3-1，在平面直角坐標系內，點A（2，0），B （5，0），動點P 與A 的距離為2，以P為直角頂點，BP為直角邊作等腰直角三角形BPM，求線段AM 的最大值及此時點P 的坐標。

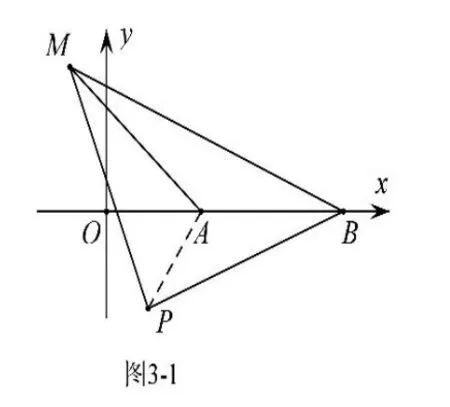
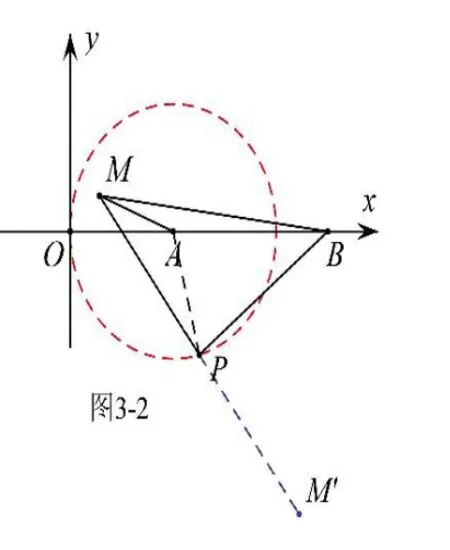
解析：由題意可知，①點P 在以A為圓心，2為半徑的圓上運動；②△PBM為等腰直角三角形,其邊長隨著點P 的運動而變化；③點M 也隨著點P 的運動而運動,雖然知道其運動軌跡為圓，但卻無法確定其圓心；④由∠BPM=90°，所以點M可能在P 的上方也可能在P 點下方，如圖3-2，求解時需分類討論。

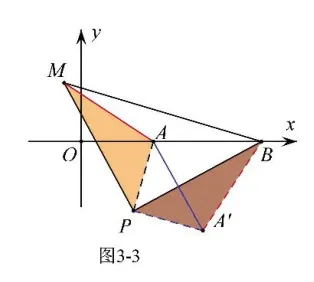
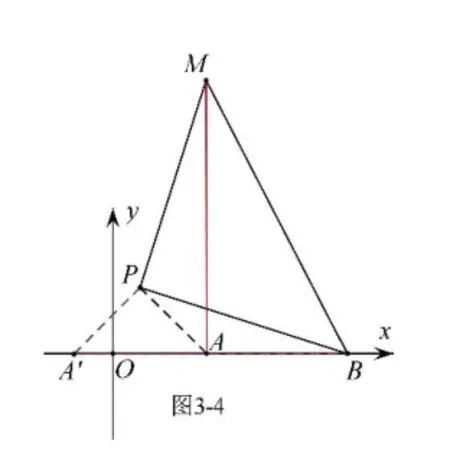
我們以PA為直角邊作等腰直角三角形APA’，如圖3-3,就將AM 轉化為A’ B 了（即AM=A’ B,求線段AM 的最大值就是求A’ B 的最大值），在△AA’ B 中，AB=3，所以A’ B 的最大值為，此時A’ 恰好在射線BA 上，P 在線段AA’的垂直平分線上.當M 在x 軸上方時，點P 坐標為（，）如圖3-4；當M 在x 軸下方時，點P 坐標為（，-）如圖3-5.

求解有關運動為背景的最值問題，要訣是①畫出草圖；②明確運動類型（沿直線運動，還是沿圓周運動？）；③若有多個動點，需進一步明確誰是主動點，誰是從動點？④無法直接求出，則需轉化。