用于混沌時(shí)間序列預(yù)測(cè)的改進(jìn)型局域線性模型

李偉民，高仲合

（曲阜師范大學(xué) 網(wǎng)絡(luò)空間安全學(xué)院，山東 曲阜 273165）

0 引 言

混沌現(xiàn)象最早由Lorentz在天氣預(yù)報(bào)研究中發(fā)現(xiàn)，之后很多人對(duì)其進(jìn)行了研究。混沌時(shí)間序列預(yù)測(cè)方法是一種非線性的時(shí)間序列預(yù)測(cè)方法，具有非線性和預(yù)測(cè)精度高等特點(diǎn)。常用的混沌時(shí)間序列預(yù)測(cè)方法有全局預(yù)測(cè)法和局域預(yù)測(cè)法[1]。全局預(yù)測(cè)法利用過去已有的全部歷史信息對(duì)未來值進(jìn)行預(yù)測(cè)，具有預(yù)測(cè)精度低和計(jì)算量大等缺點(diǎn)，因此用的較多的方法是局域預(yù)測(cè)法[2]。文獻(xiàn)[3]提出利用鄰近點(diǎn)下一步預(yù)測(cè)的平均值作為待預(yù)測(cè)點(diǎn)的下一步預(yù)測(cè)值，并提出了一種區(qū)分混沌時(shí)間序列與隨機(jī)時(shí)間序列的方法。局域預(yù)測(cè)法只利用部分歷史信息，而且局域動(dòng)力方程的擬合相對(duì)容易，計(jì)算量較小。本文改進(jìn)局域線性預(yù)測(cè)模型中的參數(shù)選取，實(shí)驗(yàn)結(jié)果表明改進(jìn)后的局域線性模型預(yù)測(cè)精度較好。

1 局域線性預(yù)測(cè)法

對(duì)已獲得的標(biāo)量時(shí)間序列x(n)，n=1,2,3,…,N，應(yīng)用相空間重構(gòu)理論，可以將標(biāo)量時(shí)間序列x(n)重構(gòu)為相空間中的軌跡X(n)，公式如下：

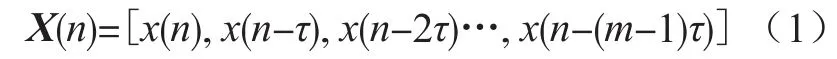
式中，n=1+(m-1)τ,2+(m-1)τ…,N；m和τ是相空間重構(gòu)的兩個(gè)重要參數(shù)，它們決定了重構(gòu)的相空間與混沌系統(tǒng)演化的近似程度。

當(dāng)重構(gòu)的相空間用于預(yù)測(cè)時(shí)，需找到X(N)的一些鄰近點(diǎn)，N表示x(n)中最后一個(gè)值的下標(biāo)[4]。在X(1)到x(n-1)的N-1個(gè)點(diǎn)中利用公式：

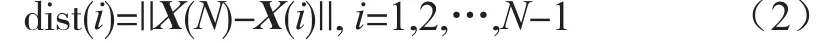
找到最近的k個(gè)點(diǎn)X(i)，dist(i)表示點(diǎn)X(N)第i個(gè)點(diǎn)的距離。鄰近點(diǎn)選好之后，可以進(jìn)行模型的建立與時(shí)間序列值的預(yù)測(cè)。

局域線性預(yù)測(cè)法是用幾個(gè)過去值的線性組合來表示將來值的一種方法，即：

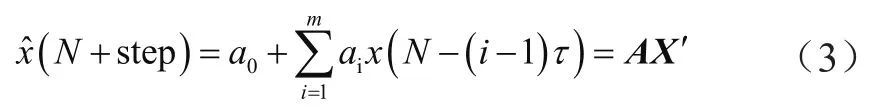
式中，A=[a0,a1,…,am]；X′=[1,x(N),x(N-τ),…,x(N-(m-1)τ)]T。它利用已獲得的鄰近點(diǎn)得到一個(gè)線性回歸方程，并用最小二乘法對(duì)線性組合的參數(shù)A進(jìn)行求解，解出后即可進(jìn)行預(yù)測(cè)。當(dāng)step=1時(shí)，即為一步預(yù)測(cè)[5,6]。

2 改進(jìn)的局域線性預(yù)測(cè)模型

對(duì)未來值的預(yù)測(cè)，一般利用如下公式：

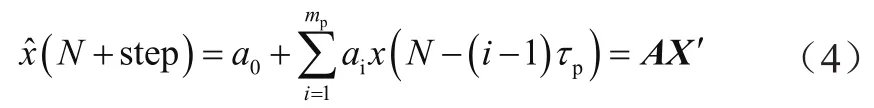
式中，參數(shù)m和τ是重構(gòu)相空間的參數(shù)。但對(duì)于相空間重構(gòu)為最佳值的m和τ，對(duì)于預(yù)測(cè)來說不一定是最佳的，即產(chǎn)生最佳預(yù)測(cè)效果的參數(shù)mp和τp可以取與m和τ不同的值[2]。

對(duì)于參數(shù)m和τ最優(yōu)值的選取，本文提出利用遺傳算法來進(jìn)行。即利用遺傳算法進(jìn)行參數(shù)取值空間中最優(yōu)參數(shù)值的搜索，搜索完成后用以下公式預(yù)測(cè)：

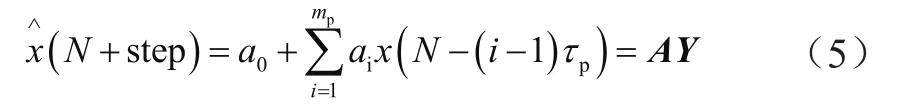
式中，Y=[1,x(N),x(N-τ),x(N-(mp-1)τp)]T；step 取為 1。預(yù)測(cè)完成后將預(yù)測(cè)值加入到原序列中繼續(xù)下一步的預(yù)測(cè)。遺傳算法的適應(yīng)度函數(shù)應(yīng)與ε(m,τ)有關(guān)，ε(m,τ)的計(jì)算如下：

其為參數(shù)取m和τ時(shí)的標(biāo)準(zhǔn)預(yù)測(cè)誤差，t為預(yù)測(cè)步數(shù)。

本文中取適應(yīng)度函數(shù)為：

即誤差越小，適應(yīng)度函數(shù)值越大。

預(yù)測(cè)流程如圖1所示。

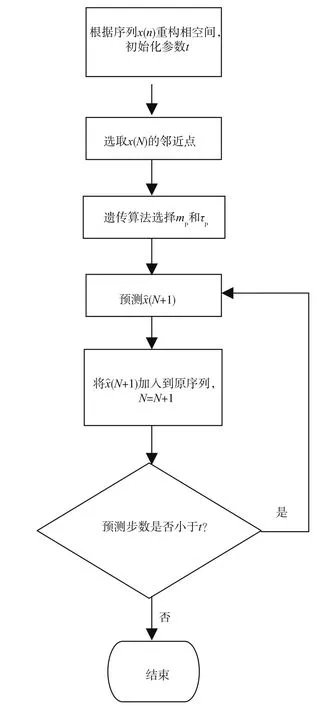
圖1 改進(jìn)的模型預(yù)測(cè)流程圖

3 實(shí)驗(yàn)分析

3.1 實(shí)驗(yàn)數(shù)據(jù)

采用洛倫茲吸引子軌跡為實(shí)驗(yàn)對(duì)象，洛倫茲吸引子軌跡的常微分方程組為：

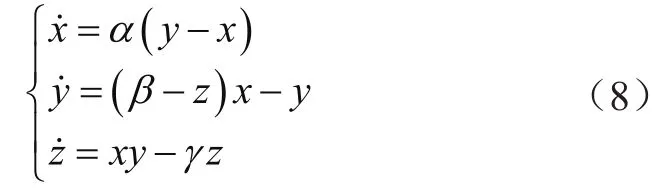
采用龍格-庫塔算法進(jìn)行積分，積分步長為0.01。取其中的x坐標(biāo)的時(shí)間序列為分析對(duì)象，即上文所述的x(n)。一共5 000個(gè)數(shù)據(jù)點(diǎn)，用前4 000個(gè)點(diǎn)建立模型，后面的點(diǎn)用于評(píng)估預(yù)測(cè)效果[7-9]。

3.2 實(shí)驗(yàn)結(jié)果

采用傳統(tǒng)的局域線性預(yù)測(cè)和改進(jìn)的局域線性預(yù)測(cè)方法的結(jié)果如下，圖2（a）和（b）分別表示傳統(tǒng)局域線性模型和改進(jìn)的局域線性模型在預(yù)測(cè)步數(shù)為50時(shí)的預(yù)測(cè)結(jié)果和誤差，傳統(tǒng)局域線性模型的ε(m,τ)值為0.010 734，改進(jìn)的局域線性模型的ε(m,τ)值為0.001 754[10]。

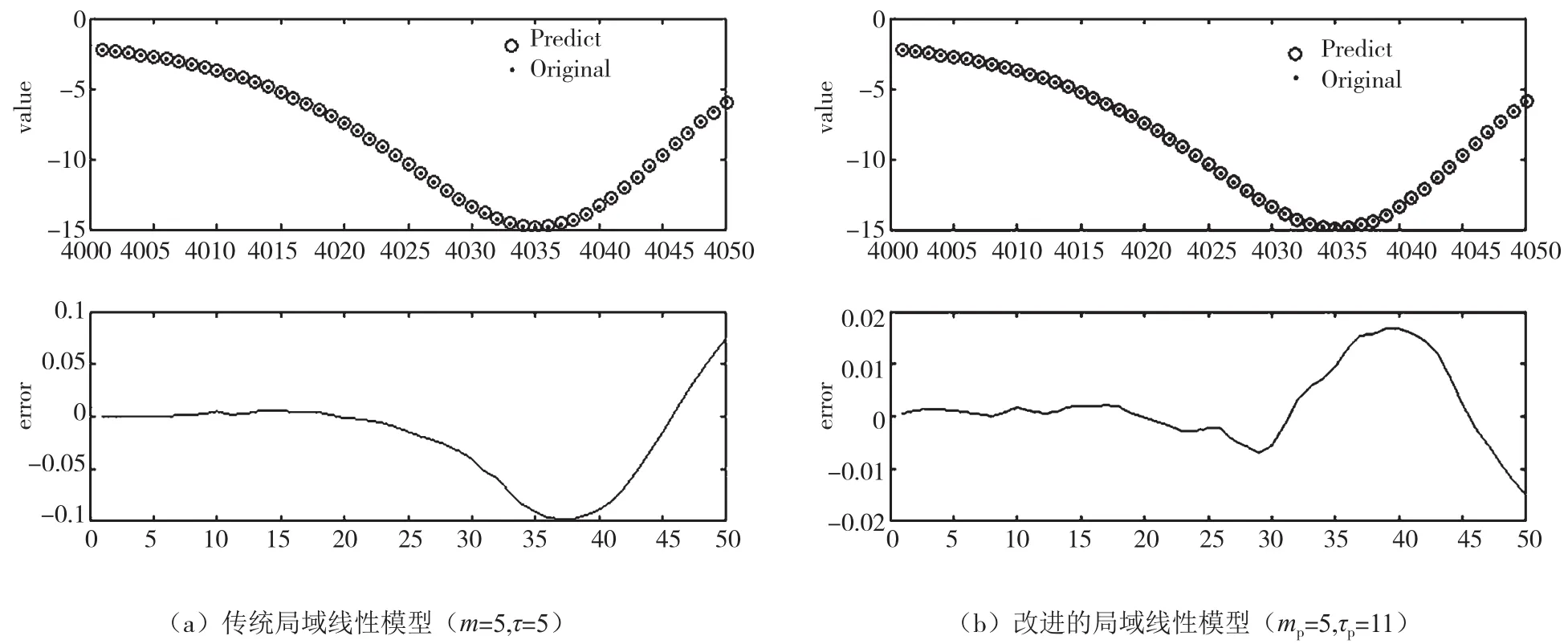
圖2 改進(jìn)的局域線性模型與傳統(tǒng)的局域線性模型預(yù)測(cè)比較

圖3（a）和（b）分別表示傳統(tǒng)局域線性模型和改進(jìn)的局域線性模型在預(yù)測(cè)步數(shù)為100時(shí)的預(yù)測(cè)結(jié)果和誤差，傳統(tǒng)局域線性模型的ε(m,τ)值為0.068 439，改進(jìn)的局域線性模型的ε(m,τ)值為0.018 721。

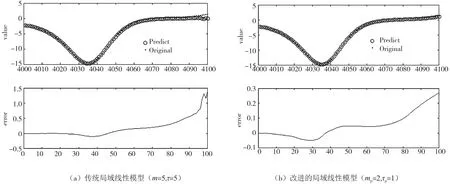
圖3 改進(jìn)的局域線性模型與傳統(tǒng)的局域線性模型預(yù)測(cè)比較

4 結(jié) 論

局域預(yù)測(cè)法是混沌時(shí)間序列預(yù)測(cè)的一種有效方法，傳統(tǒng)局域線性預(yù)測(cè)模型中參數(shù)和τ是和相空間重構(gòu)的參數(shù)和τ一樣，改進(jìn)的局域線性預(yù)測(cè)模型中參數(shù)經(jīng)過遺傳算法優(yōu)化后使得預(yù)測(cè)效果有了提升，說明了遺傳算法和重新選取的參數(shù)的有效性。