鋪層參數對復合材料電池箱蓋模態和穩定性的影響
劉傳波,陳傲杰,王穩,肖灑
(1.武漢理工大學機電工程學院, 湖北武漢 430070;2.湖南三合汽車新材料有限公司,湖南長沙 410323)
0 引言
隨著社會環保意識不斷增強,我國對新能源汽車的政策支持不斷增加,新能源汽車的生產規模不斷壯大,但目前電池儲存的能量受到限制,續航里程不足、整車成本高,嚴重阻礙新能源汽車發展。輕量化成了解決續航里程的重要手段之一。纖維增強復合材料汽車零部件由于密度低、比強度高、耐腐性強等特點成為汽車零部件的主要發展方向。趙曉昱和張樹仁[1]利用剛度等效設計方法,用復合材料代替金屬材料對電池盒進行輕量化設計。HARTMANN等[2]通過有限元軟件對電池箱的結構進行了優化設計,不僅提高電池箱的固有頻率,而且將質量降低了20%。對于復合材料而言,鋪層方式對產品的性能有很大的影響,李仁年和劉有亮[3]通過對風力機葉片進行鋪層設計,分析出增加葉片梁帽位置的鋪層層數對風機的固有頻率比其他位置的影響大。JIANG等[4]對T700/2510織物和單向復合正弦波板在軸向準靜態沖擊下的破壞模式和能量吸收特性進行了數值研究,分析纖維角度的變化對復合正弦板壓潰性能的影響。段端祥和趙曉昱[5]利用有限元軟件Optistruct對碳纖維復合材料電池箱鋪層順序進行優化,得到最佳的鋪層分布方案,輕量化效果明顯。目前國內外主要通過采用復合材料對汽車零部件進行輕量化設計,關于復合材料鋪層方式對電池箱蓋穩定性能的影響研究較少。
本文作者利用有限元分析軟件對電池箱蓋進行鋪層比例、鋪層順序和鋪層厚度設計,并通過對纖維增強材料鋪層方案分析,探究鋪層參數對電池箱蓋模態及穩定性能的影響。
1 復合材料電池箱蓋鋪層設計
1.1 鋪層設計原理分析
復合材料的鋪層設計實際上就是層合板設計,由單層的特性來確定層合板中各纖維層的鋪設角度、鋪設層數以及鋪層順序。由于纖維和基體材料性質差異很大,在單層復合材料層中沿纖維方向的性能和垂直纖維方向的性能變化很大,形成了正交各向異性性能[6]。
層合板設計任務是根據單向板的性能確定層合板中鋪層的鋪設方向、各鋪層的鋪層比例、各定向鋪層的順序等。對于層合板性能而言,不僅與各鋪層的材料性能有關,而且還與各鋪層的材料取向、鋪設比例以及各層的堆疊順序有關。因此,通過改變各鋪層的材料主方向及疊放順序設計出所需力學性能的層合板,而不需要改變鋪層的材料情況[7-8]。
1.2 鋪層方案設計
本文作者研究的纖維增強材料電池箱蓋是采用某玻璃纖維/環氧預浸料材料層疊固化而成,將電池箱蓋的三維模型導入ANSYS中進行網格劃分和鋪層方案設計,有限元模型如圖1所示,纖維每層厚度為0.3 mm,材料性能如表1所示。

圖1 電池箱蓋有限元模型
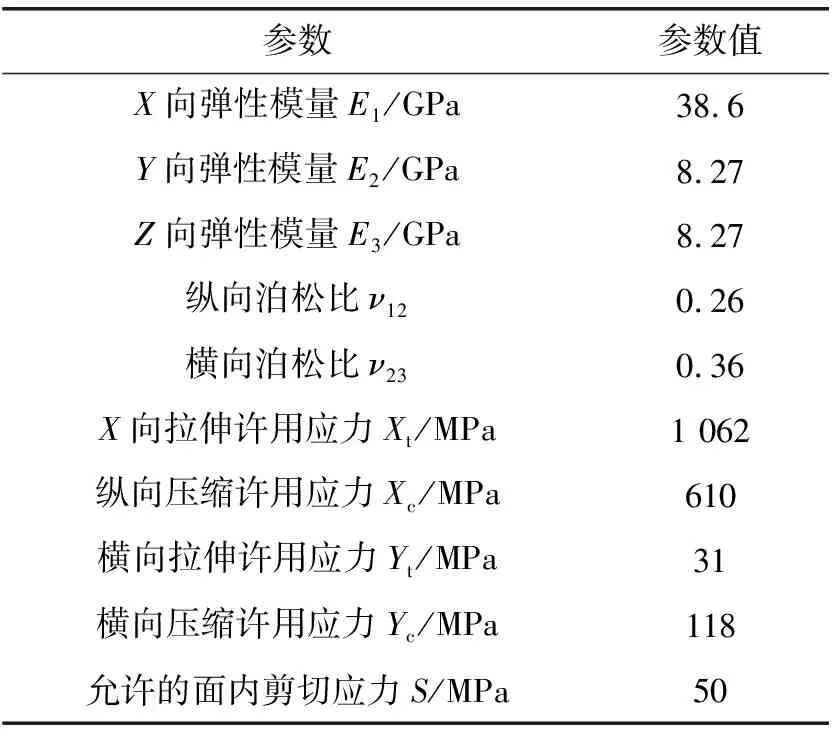
表1 研究中使用的玻璃纖維的材料力學參數
對于復合材料纖維鋪層設計而言,鋪層方案存在多種可能性,通過簡化,設計中采用0°、45°、-45°三個方向進行鋪層,通過設計不同鋪層比例(A1、A2、A3)及不同鋪層角度(A2、B1、B2)和鋪層厚度(B1、C1、C2)幾種方案來探究鋪層比例、鋪層角度和鋪層厚度對復合材料電池箱蓋模態及力學性能的影響,其中鋪層方案表示方法為[0m/(±45)n]s(m、n≠0,m表示 0°連續層數,n表示±45°層鋪層數,s表示對稱鋪層)。

表2 電池箱蓋鋪層方案
2 模態分析
2.1 模態分析有限元理論
通過有限元法[9-11]對系統結構劃分網格,將無限自由度的系統轉化成多自由度的系統,得到多自由度的運動微分方程:
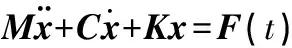
(1)
式中:M為系統質量矩陣;C為系統阻尼矩陣;K為系統剛度矩陣;F(t)為結構的激振力向量。
文中電池箱蓋采用靜態模態分析,無外力作用,即F(t)=0;并且在求解結構自由振動的固有頻率和振型時,一般阻尼對它的影響不大,可忽略阻尼對系統的影響,得到無阻尼自由振動方程:
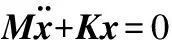
(2)
對應的結構自振頻率方程:
(3)
式中:ωn為結構固有頻率。
對于復合材料電池箱蓋是各向異性體,單元剛度矩陣為各向異性單元,單元剛度矩陣:
(4)
式中:D為彈性矩陣;Bi、Bj分別為應力、應變關系矩陣。
(5)
式中:m為單元內鋪層數;Dj為第j個鋪層的彈性矩陣;tj為第j個鋪層的厚度;h為單元厚度。
對于復合材料電池箱蓋來說,電池箱蓋鋪層層數、鋪層順序、鋪層方向角均影響電池箱蓋的剛度矩陣K;殼鋪層厚度改變會影響殼結構的質量矩陣。這些鋪層因素的改變最終影響電池箱蓋結構頻率發生變化。
2.2 鋪層方式對模態的影響
在有限元軟件ANSYS Workbench中,對所建有限元模型進行約束模態分析。選取電池箱蓋法蘭邊作為固定約束位置,選取計算電池箱蓋約束模態的階數為5階,分析不同鋪層方式下的模態值。表3是不同鋪層方案下的1~5階模態固有頻率。
(1)A1、A2、A3三種鋪層方案是鋪層順序和總層數相同,±45°的纖維鋪層比例依次增加,從表3中可看出;電池箱蓋的模態固有頻率關系是A3>A2>A1,表明隨著±45°纖維層比例的增加,電池箱蓋的固有頻率不斷增加。(2)A2、B1、B2三種鋪層方案采用不同的鋪層順序,總層數和鋪層比例相同,電池箱蓋的一階固有頻率關系為B1>B2>A2,其中B1、B2采用對稱鋪層的方式,可看出采用對稱鋪層的一階固有頻率高于非對稱鋪層;比較方案B1和B2的模態值,B1的固有頻率高于B2的固有頻率,表明0°鋪層纖維在外側時的固有頻率強于±45°纖維在最外層時的固有頻率。(3)鋪層方案C1、B1、C2鋪層厚度不同,厚度關系為C1>B1>C2,從表3可看出電池箱蓋的固有頻率關系為C1>B1>C2,可以得出隨著鋪層厚度的增加,電池箱蓋的固有頻率不斷增加。
另外,根據計算結果,盡管采用不同的鋪層方案,但具有相同的振型;電池箱蓋的一階振型為中部局部振動,二階振型為前后振動,三階振型為前、中、后三部分振動,四階振型為左右振動,五階振型為殼大面積振動。鋪層方案B1前五階約束模態振型如圖2所示。

圖2 鋪層方式B1振型分布
3 穩定性分析
新能源汽車在行駛過程中,電池箱會受到橫、縱、垂向3個方向的振動,分別用X、Y、Z向來表示,其中沿Z向的振動最大。本文作者根據GB/T 31467.3-2015中X、Y、Z方向的振動頻率與功率譜密度,通過有限元分析軟件模擬電池箱蓋在運動過程中的隨機振動,探究不同鋪層方式下的最大應力及最大變形量,X、Y、Z三個方向隨機振動PSD如圖3所示[12-14]。
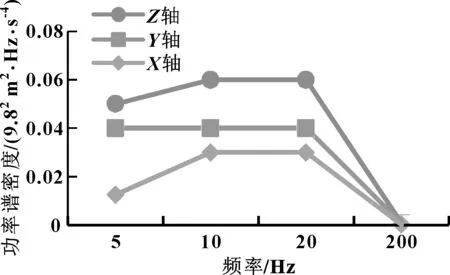
圖3 X、Y、Z方向隨機振動PSD密度譜
3.1 鋪層方式對應力的影響
通過固定電池箱蓋的法蘭邊面,然后根據功率譜密度對電池箱蓋施加Z向的隨機振動,鋪層方案如表2所示,研究不同方案下電池箱蓋所受的最大應力,圖4是不同鋪層方式下電池箱蓋所受的最大應力。
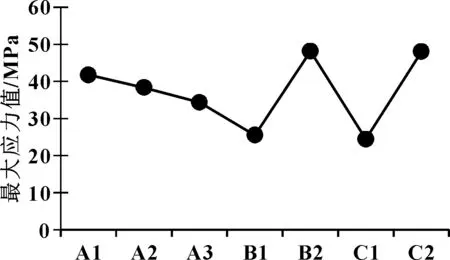
圖4 不同鋪層方式下的最大應力
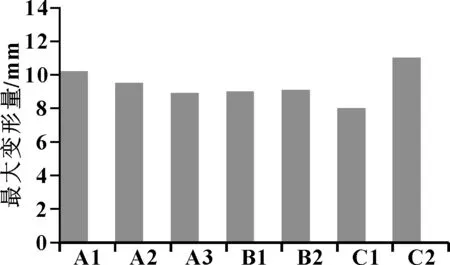
從圖4可看出:±45°纖維由40%增加到60%時,電池箱蓋受到的最大應力降低了9.2%,當纖維比例從60%增加到80%時,其最大應力降低了10.5%,表明隨著±45°體積分數的增加,電池箱蓋的強度不斷增加;通過對比不同鋪層順序方案A2、B1、B2,其最大應力關系為B1 圖5 不同鋪層方式下的應力云圖 圖6是不同鋪層方式對電池箱蓋的最大變形量的影響。 圖6 不同鋪層方式下的最大變形量 從圖6可看出:纖維鋪層比例對電池箱蓋的最大變形量的影響與電池箱蓋受到的最大應力值類似,鋪層方案A1、A2、A3最大變形關系是A3 基于復合材料鋪層基本原理,采用ANSYS軟件對不同鋪層方案下殼的模態及力學性能進行分析,對比不同鋪層下的固有模態、最大應力值及最大變形量,并繪制不同鋪層方案下的應力云圖,得出了不同鋪層方式對電池箱蓋性能的影響規律。 (1)采用不同的鋪層方案可以改變電池箱蓋的固有頻率,選擇合適的鋪層方案可以有效避免共振現象的發生。 (2)隨著±45°鋪層比例的增加,電池箱蓋的模態和穩定性不斷增強;鋪層順序對電池箱蓋模態量影響效果不顯著,但對最大應力值有明顯的影響,當0°纖維在最外側時比±45°纖維在最外側時應力值降低47%。 (3)采用對稱鋪層有利于提高電池箱蓋的固有頻率,電池箱蓋外層纖維鋪層方式對箱蓋的應力值影響較大,隨著鋪層厚度的增加,電池箱蓋的穩定性能不斷提升。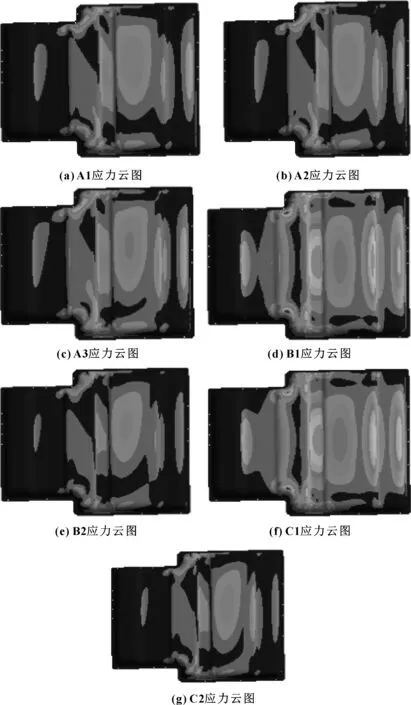
3.2 鋪層方式對變形量的影響
4 結論

