格柵加筋膨脹土拉拔試驗測試值的數值模擬

萬 亮，楊和平

(1. 長沙理工大學 道路結構與材料交通行業重點試驗室，湖南 長沙 410076；2. 安徽省農墾集團有限公司，安徽 合肥 230000)

0 引言

隨著土中加筋技術的不斷發展，許多不同類型的材料被用于加筋土中，其中包括：鋼帶、鋼筋網格、土工織物和土工格柵等，目的都是通過提高土與筋材間的作用力，從而增大土的側向約束[1]。特別是格柵因其與土粒間的摩擦咬合作用較強，以及具有很好的耐酸、耐堿、耐腐蝕、抗老化等特點，故在歐美及日本的土木工程中已得到普遍應用[2]。國內的加筋土設計，大多采用筋材在無側限條件下的應力-應變關系，取對應于破壞應變2%～5%的應力值，或直接取40%～50%的最大應力值作為其設計強度。實際研究表明，埋于土中的土工合成材料受到側限壓力的作用，其應力-應變關系完全有別于無側限時的性狀，有些合成材料在小應變狀態下，其有側限抗拉強度有可能是無側限抗拉強度的3～4倍，顯然，經驗取值的方法有很大的任意性，難以符合實際。目前較合理的方法是采用室內試驗獲得筋土間最大拉拔力。《土工合成材料測試規程》(SL 235—2012)[3]已明確提出，直剪摩擦試驗不適合土工格柵等材料，拉拔摩擦試驗才適用確定各種性質和狀態的土與各類土工格柵的相互作用。然而由于拉拔試驗儀器、操作步驟均沒有統一標準，試驗過程耗費大量的物力、財力和時間成本，且存在一定的安全風險，不少學者試圖采用數值模擬來獲得筋、土間拉拔力，但在數值模擬過程中對分析筋土間相互作用十分重要的參數，其獲取的渠道又各有不同：羊曄、張智超、Hasthi等[4-9]采取的是經驗估算；徐晗、Yu、賴咸根等[10-13]沒有明確提供所用參數的來源；Bathurst、鄭俊杰、Ghazavi等[14-17]則是通過文獻獲得。由于一些參數取值與實際不符，導致模擬結果與實測值有不小誤差， 但仍客觀反映了開展數值模擬研究的必要性。正如龔曉南[18]所言，“計算機仿真技術是利用模型對實際系統進行的試驗研究，是十分重要、甚至必不可少的工具”。而目前經系統試驗獲得數值計算參數后再做數值模擬研究，尤其是開展加筋膨脹土拉拔試驗后再進行數值模擬的研究還十分鮮見。

本研究先采用自主研發的大型數控拉拔試驗系統(CS-LB01)完成單向土工格柵加筋膨脹土拉拔試驗和膨脹土直剪試驗，以獲得數值模擬所需參數。進行格柵測點位移監測和不同上覆壓力的拉拔試驗，用FLAC3D模擬拉拔試驗中筋土間的力學行為，探究由數值模擬獲取界面相互作用發生、發展的可行性及與試測值的偏差，嘗試用數值模擬快速確定加筋土中筋材作用的最大拉拔力，以節省試驗所需經濟和時間成本，為工程設計與施工提供依據和便利。

1 試驗設備、材料及方案

1.1 拉拔試驗

試驗采用自主研發的大型數控拉拔試驗系統(CS-LB01)[19]，其主要特點：(1)尺寸大：120 cm (長)×50 cm(寬)×50 cm(高)；(2)拉拔過程可實施恒速或恒力控制；(3)適合各類填料；(4)加載方式采用上、下氣囊并配置穩壓伺服系統的加載方式更合理；(5)消除了箱側壁摩擦對試驗的影響；(6)數據采集系統可精確獲取筋材位移與拉力的關系。CS-LB01的主要性能和測試指標見表1。試驗接觸面積大、能施加較大荷載和拉筋位移大是其顯著優勢。整個系統由拉拔測試主機、數據采集系統、壓力伺服控制及壓實與起吊輔助設備4部分組成(見圖1)。

表1 CS-LB01主要性能指標

圖1 CS-LB01結構組成示意圖(單位：mm)

1.2 試驗材料

膨脹土填料為廣西典型的寧明土，其基本土性指標見表2。土工格柵的其物理特性指標見表3。圖2為其網格結構，廠家提供的拉力與應變關系見圖3。

1.3 試驗方案設計

為開展加筋土試驗的數值模擬分析，先設計直剪與系列上覆壓力下的拉拔試驗，以取得模擬所需計算參數，后設計驗證數值模擬與實測值相符與否的拉拔試驗。

表2 試驗土的基本土性

表3 土工格柵物理性質

圖2 單向土工格柵的網格結構

圖3 TGDG35格柵的拉力與應變關系

1.3.1直剪試驗

因建立本構模型用到試驗土樣抗剪強度相關參數，按土工試驗規程對25%含水率在重型擊實90%壓實度條件下制備的寧明膨脹土土樣，分別在上覆壓力50，100，150，200 kPa下完成直接剪切試驗。

1.3.2拉拔試驗

(1)為獲得試驗數值模擬所需筋土界面相互作用計算參數，即單位面積剛度系數k和填土的抗剪強度c及摩擦角φ值，制備25%含水率寧明土樣，在90%壓實度條件下、分別完成上覆壓力為50，100，150，200 kPa下的恒速拉拔(1 mm/min)試驗，具體方案見表4。

表4 獲取數值模擬所需參數的試驗方案

(2)為檢驗數值模擬與拉拔測試值之間的符合程度，同樣設計1 mm/min拉拔速度的25%含水率寧明土在上覆壓力75 kPa作用下的拉拔試驗(方案見表5)。測試時用5個位移傳感器分別記錄拉拔過程中受拉格柵上監測點5的位移發生及發展變化(具體布設見圖4)，監測點1～5分設在平鋪格柵中部距夾具端0，15，30，45，60 cm處。

表5 驗證數值模擬的試驗方案

圖4 位移監測點位置示意圖

2 測試結果及分析

2.1 直剪試驗

按《公路土工試驗規程》(JTGE40—2007)[20]，在4聯剪切儀上完成50，100，150，200 kPa上覆壓力的直剪，得到各剪應力與位移關系曲線(見圖5)。圖6為分析所得最大剪應力與上覆壓力關系，可知寧明土抗剪強度：C=90.5 kPa，φ=24.6°。

圖5 剪應力與剪切位移關系曲線

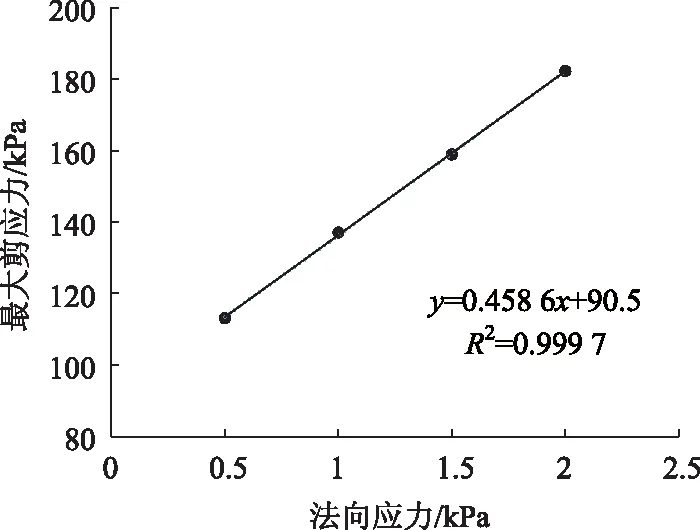
圖6 最大剪應力與上覆壓力關系(直剪試驗)

2.2 拉拔試驗

2.2.1方案1測試結果

按表4試驗設計方案，對埋入尺寸60 cm×42 cm的TGDG35格柵，分別在50，100，150，200 kPa上覆壓力下完成恒速拉拔，測試結果見圖7和表6。

圖7 不同上覆壓力下的拉拔曲線

表6 不同上覆壓力下的最大單寬拉拔力

將拉拔力除以格柵的埋入面積，可得筋、土界面間剪應力τ。若繪制該界面剪應力與拉拔位移關系曲線將與圖7極相似(橫坐標取值不變，縱坐標值均提高1.67倍)，故按同樣取值擬合方法，可確定最大界面剪應力與上覆壓力呈線性關系(見圖8)，此時筋土界面的黏結強度為3.78 kPa，摩擦角為12.47°。根據FLAC3D5.01 手冊[21]中定義的單位面積剛度系數k及其求算方法(見圖9)，可求得在50，100，150，200 kPa上覆壓力作用下，筋土界面間的剛度系數k分別為2.58×107，2.67×107，2.78×107，2.78×107N/m3。因各k值的數量級均為107，量級前各數值的細小差別對數值模擬結果的影響不大，故本次模擬將這4個k值平均，取剛度系數k=2.7×107N/m3。

圖8 最大剪應力與上覆壓力關系(拉拔試驗)

圖9 剪應力與相對剪切位移關系示意圖

2.2.2方案2測試結果

完成75 kPa壓力下寧明土的拉拔試驗，將拉力換算成單位寬度，繪出單寬拉拔力與拉拔位移關系曲線(圖10)。可以看出，位移達到2 mm前，拉拔力上升速度較快，隨后升速變緩，位移達到9.5 mm時拉拔力出現峰值(12.2 kN)，接下來呈下降趨勢。

圖10 單寬拉拔力與拉拔位移曲線(上覆壓力為75 kPa)

通過埋設于格柵上的5個位移傳感器，可獲得拉拔過程中各監測點的位移變化(見圖11)，其橫坐標拉拔位移和監測點1的位移相同，各監測點起始位移見表7，最終各測點拉拔線呈45°等斜率上升，表明土中加筋是整體按1 mm/min速率移動。

圖11 格柵不同監測點處位移曲線

3 數值模型及材料參數

3.1 膨脹土模型及參數

摩爾-庫倫模型適用于在剪應力下屈服，且剪應力只取決于最大、最小主應力，第2主應力對屈服不產生影響的材料。故本試驗的膨脹土填料采用FLAC3D中的內置Mohr-Coulomb本構模型，其最大優點是：模型所用參數通過常規直剪試驗就能確定，且模型參數的物理意義容易理解。建模所需的膨脹土計算參數取值見表8。

表7 各監測點起始位移(單位：mm)

表8 膨脹土計算參數

3.2 土工格柵模型及參數

眾所周知，單向土工格柵材料為韌性材料，只能受拉，不能受壓，且埋于土中正常工作時所受拉力遠小于其抗拉強度，其應力-應變關系在線彈性范圍內，故直接采用FLAC3D內置的土工格柵單元(geogridSEL)來模擬，其特點是能承受薄膜荷載而不能抵抗彎曲荷載，每個土工格柵單元的力學參數，可分解為格柵材料自身結構響應參數及格柵單元與填料實體單元間的相互作用參數。根據TGDG35格柵生產廠家提供的數據及本次膨脹土加筋拉拔試驗的實測結果，分析確定兩種計算參數的取值(見表9)。

表9 土工格柵及筋土界面計算參數

3.3 建立拉拔試驗計算模型

根據FLAC3D5.01使用手冊中關于拉拔試驗的建模步驟，結合本拉拔試驗的邊界條件建模。拉拔箱體四周固定，而頂面和底面需施加測試荷載，箱體幾何尺寸為：長120 cm，寬50 cm，高50 cm。埋入土中的格柵面積為：長60 cm×寬42 cm。選用FLAC3D5.01版進行數值模擬計算，確定試驗模型由600個膨脹土單元體和72個土工格柵單元體組成，如圖12所示。首先建立24×5×5的網格，然后調整y方向膨脹土單元的間距使之適應寬42 cm的格柵單元，再調整z方向的膨脹土單元間距以保證土工格柵位于單元體的中心。通過以上反復調整，最終確保施加在埋入格柵上的約束力等于其相應深度的實際值。

圖12 土工格柵拉拔試驗模型

4 數值模擬結果及分析

數值模擬采用如下順序：固定箱體的側面和底部，安裝土工格柵(先在頂面創建，后將它重新移至中心位置)，將膨脹土自身的重力激活并讓它在重力作用下達到自然平衡，然后向填土頂部表面施加豎向恒定壓力(初始狀態時該壓力值為0)，并達到新的平衡。此階段填土頂面的下沉量為0.05 mm，中部平鋪格柵處的下沉量為0.0 3mm(如圖13(a)所示)，再施加75 kPa豎向荷載后填土頂面下沉了1 mm，相應中部格柵處的下沉量為0.43 mm(如圖13(b)所示)，至此即在拉拔試驗正式開始前，使在土中水平攤鋪的格柵已在箱體高度正中位置就位。

圖13 土體位移云圖(單位：m)

4.1 數值模擬結果

本拉拔試驗的模擬是通過對x=1.2 m處土工格柵單元節點施加速率為1 mm/min的水平位移來實現的。測試期間，軟件能對施加的力及其節點位移實施自動監控，該力就是作用于格柵節點上所有不平衡力的合力，將它除以埋入格柵的寬度即得到格柵單寬拉拔力，本次試驗模擬所得的單寬拉拔力與拉拔位移關系見圖14，其對應的單寬拉拔力云圖見圖15。

圖14 單寬拉拔力與拉拔位移曲線(上覆壓力為75 kPa)

圖15 土工格柵單寬拉拔力云圖(上覆壓力為75 kPa)(單位：m)

通過軟件自帶的監測功能，可數值模擬獲得拉拔過程中格柵各監測點的位移變化線，見圖16。圖中的監測點1～5與試驗監測點位置相對應。最終位移云圖模擬結果見圖17。

圖16 格柵不同監測點處位移曲線(上覆壓力為75 kPa)

圖17 土工格柵位移云圖(上覆壓力為75 kPa)(單位：m)

4.2 單寬拉拔力的對比分析

為方便分析對比，圖18中將單寬拉拔力隨拉拔位移變化的數值模擬結果(圖14)與試驗測試的結果(圖10)繪制在一起，可看出兩者最大的差別是試驗曲線起始點處的單寬拉拔力遠不為0，原因是實施拉拔試驗前需用夾具將格柵端部夾緊，此刻即對格柵作用了一個5.3 kN的夾緊力，而理論上講數值模擬時格柵初始拉力是從0開始，兩者之差距只能在隨后的拉拔位移實施中逐步消化。分析圖18中兩曲線的發展變化，它們的上升趨勢、增速及達到的峰值基本相同，穩定后兩者最大單寬拉拔力分別為12.3 kN與12.2 kN，非常接近，尤其對應最大拉力的拉拔位移均約9.5 mm，說明對拉拔作用力的數值模擬結果與實際試測結果相符。

圖18 單寬拉拔力數值模擬與試驗結果對比曲線

4.3 拉拔位移的對比分析

同樣，將監測點位移的數值模擬結果(圖16)與試驗結果(圖11)放到一起做比較(見圖19)，可看出監測點1的兩根位移線完全重合，而監測點2，3，4，5起始位移點的模擬值均稍大于實測值，原因是在數值模擬這些點起始位移時，出現不平衡力不收斂，格柵監測點有少量位移(約2 mm)后，不平衡力逐漸收斂，此后各測點均以1 mm/min的速率移動，相鄰測點的間距逐漸減少，數值模擬線與實測線高度吻合，充分說明采用數值模擬確定拉拔試驗中格柵監測點在膨脹土中的位移軌跡合適、可行。

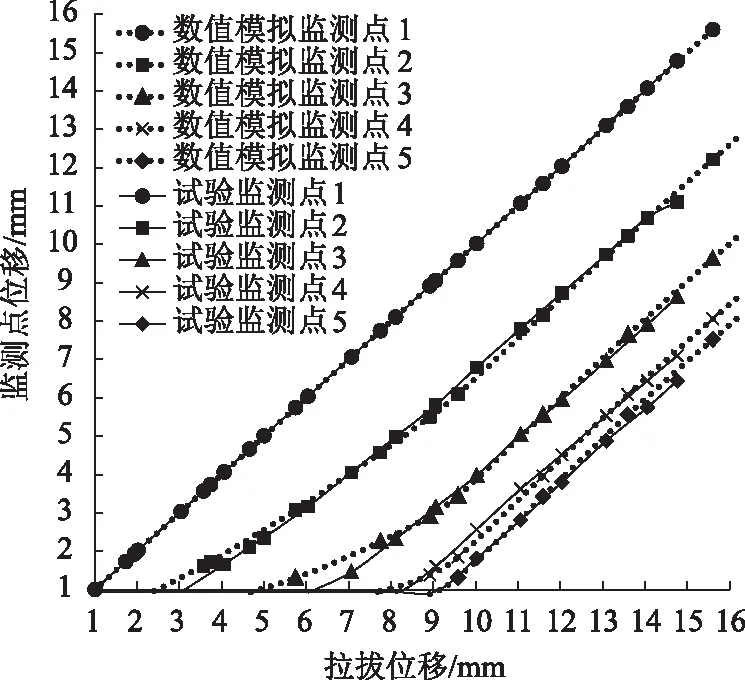
圖19 監測點位移數值模擬與試驗結果對比曲線

此外，以拉拔位移達12 mm為例，進一步將拉拔試驗各監測點發生的位移與數值模擬的對應值做比對分析(結果見表10)，不難看出沿土中格柵埋入方向，從前往后兩組數據均顯示相鄰測點間的位移間距在逐漸減小，拉拔實測值與數值模擬值有著良好的一致性，再次表明采用數值模擬來獲取單向土工格柵加筋膨脹土拉拔試驗的測試值合理、可行。

表10 各監測點位移對比值(拉拔位移12 mm)

5 結論

(1)用CS-LB01做一組單向土工格柵加筋膨脹土拉拔試驗，需約600 kg一定含水率膨脹土，試驗前筋材的準備、填料分層填壓等要耗費大量人力物力，移動笨重箱體與壓實機具需借助大型吊運機具，且試驗操作尚存一定安全風險，因此，隨著計算機術的日漸成熟，采取數值模擬獲取試驗測試結果是未來的發展趨勢。

(2)數值分析的合理、可靠性取決于計算模型及參數設計的合理性。本研究先由直剪、拉拔試驗分別確定填料及筋、土界面建模所需參數，采用FLAC3D程序進行數值模擬，與變上覆壓力單向土工格柵加筋膨脹土拉拔試驗測試結果做對比，兩者一致性良好，成功地實現了拉拔測試值的數值模擬。

(3)所建計算模型較好地反映了格柵加筋膨脹土的受力變形特點，易于用有限元計算實現，其穩健可靠且快捷的數值模擬與優化，使分析筋土間相互作用的過程大為簡化，用于實際加筋工程設計可節省大量試驗時間、成本及原材料。

(4)準確參數的輸入，使得數值模擬能更便捷、直觀地展示拉拔試驗過程中土、筋材及筋土間應力與應變的發生、發展與變化，為獲取最大拉拔力及分析作用機理提供便利。