基于真實齒面的直齒錐齒輪加載接觸分析研究*

呂 勝

(中國航發湖南動力機械研究所，湖南 株洲 412002)

0 引 言

直齒錐齒輪廣泛應用于航空發動機，它具有傳動平穩、承載能力高等特點，但其嚙合性能分析非常復雜，與機床結構、加工參數、機床參數設置、加載變形以及裝配誤差等都有關系，直齒錐齒輪的嚙合性能主要用齒輪副接觸印痕的形狀、位置、和大小來控制。

某航空發動機裝配試車后分解檢查發現附件傳動系統直齒錐齒輪接觸印痕偏離設計要求，必須對直齒錐齒輪返廠修磨，并重新工廠試車，造成成本增加和交付時間延長。筆者通過基于真實齒面的直齒錐齒輪模型進行加載接觸仿真分析，提前預知真實齒面的工作接觸印痕，避免發動機因直齒錐齒輪接觸印痕不合格問題而造成返廠分解和錐齒輪返修，提高工廠試車合格率。

1 錐齒輪真實齒面建模

錐齒輪真實齒面建模分坐標變化、大輪齒面反求、小輪齒面反求和輪坯建模四個步驟進行。

1.1 坐標變換

采用三坐標測量機測量錐齒輪真實齒面離散點數據，坐標系規定為：坐標原點在節錐頂點，Z軸與軸線重合，從大端指向小端，X軸沿徑向指向齒輪表面，Y軸按右手規則確定[1]，本文接觸印痕分析采用的坐標系為：坐標原點也在節錐頂點，但X與軸線重合，從小端指向大端，Z軸沿徑向指向齒輪齒面，Y軸按右手規則確定，因此需要進行坐標變換，設齒面在三坐標測量坐標系中徑矢為rsource,本文嚙合分析的坐標系中徑矢為r，則兩者之間的坐標變換矩陣為:

1.2 大輪齒面反求

按以下三個步驟進行大輪齒面反求：①初選刀盤直徑，上、下各取兩個刀盤直徑，檢驗齒長方向的網格點吻合程度，確定刀盤直徑；②然后以齒根角、壓力角及刀盤半徑三者為優化變量，進行凹面參數的連續優化；③以壓力角、刀盤半徑兩者為優化變量，進行凸面參數的連續優化。在試探齒面在最小二乘意義下接近實測齒面之后，將反求出來的齒面拓展至名義邊界[2]，得到大輪凹面和凸面優化后如圖1所示,其中反求齒面與實測齒面的最大法向誤差值不超過0.005 mm。

1.3 小輪齒面反求

按照1.2中方法初步建立小輪齒面，以嚙合性能參數為優化設計變量，采用局部綜合法優化小輪齒面，使其逐漸逼近真實齒面[3]，建立的數學模型為：

式中：Fmin(φ2,r1,r2)表示與大輪轉角和齒面有關的齒面最小間距；Psurface和Gsurface分別為小輪和大輪齒面。

得到小輪優化后的凹面和凸面如圖2所示。

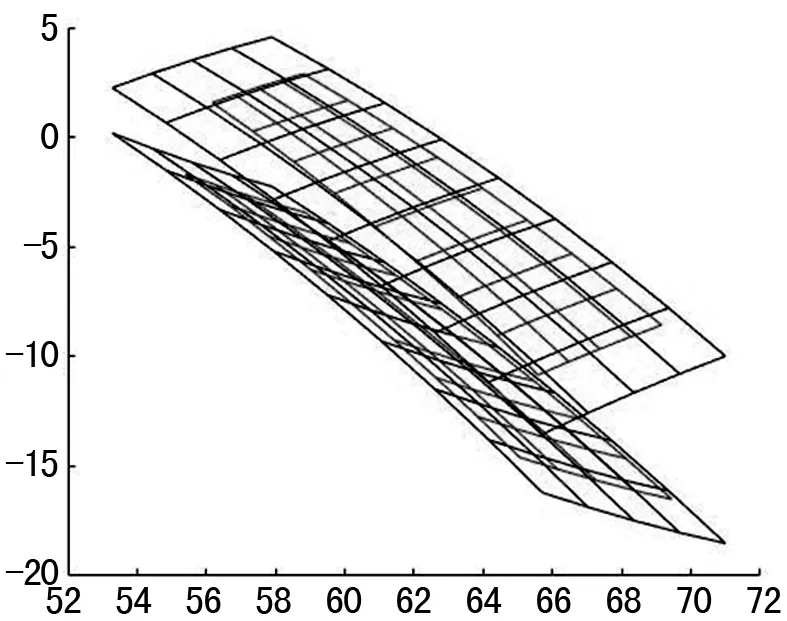
圖1 優化后大輪真實齒面建模

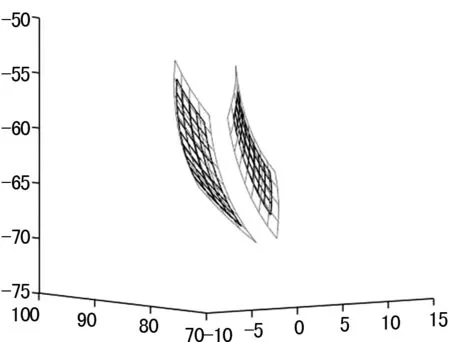
圖2 優化后小輪真實齒面

1.4 基于真實齒面的錐齒輪幾何建模

輪坯幾何建模主要依據設計圖樣上給定的參數，此對直齒錐齒輪主要設計參數如表1所列。

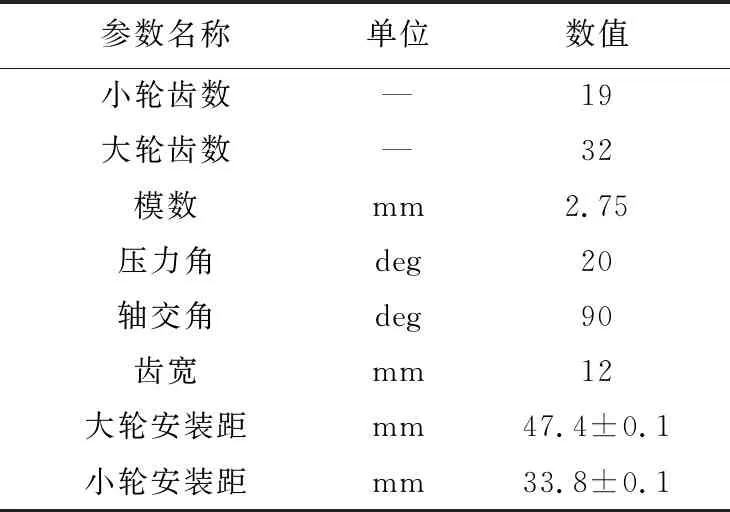
表1 直齒錐齒輪齒輪主要設計參數

2 加載接觸仿真分析建模

將基于真實齒面的錐齒輪模型導入ANSYS中進行直齒錐齒輪加載接觸分析，其邊界條件及加載方式如下：在大輪內圈與兩個外側面的節點組件施加全約束，在小輪節錐的錐頂處定義一個單節點六自由度的點單元，設置小輪輪齒的內圈和兩個外側面的節點組件與錐頂處的點單元固連，在錐頂的點單元上施加徑向和軸向約束并保留其繞軸的旋轉自由度[4]。在網格劃分過程中，輪體應順著輪齒的方向扭曲，盡量減少網格的畸變，本模型采用8節點單元，總節點數為18 880，總網格數為11 536，具體的網格劃分如圖3所示。

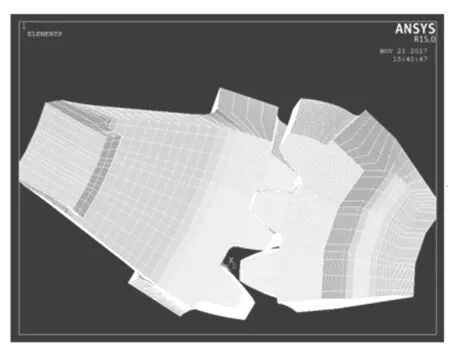
圖3 三齒有限元模型

3 加載接觸仿真分析及驗證

設置求解選項，打開大變形效應，打開自動時間步長跟蹤，進入求解，得到大、小輪接觸印痕仿真結果如圖4、5所示。

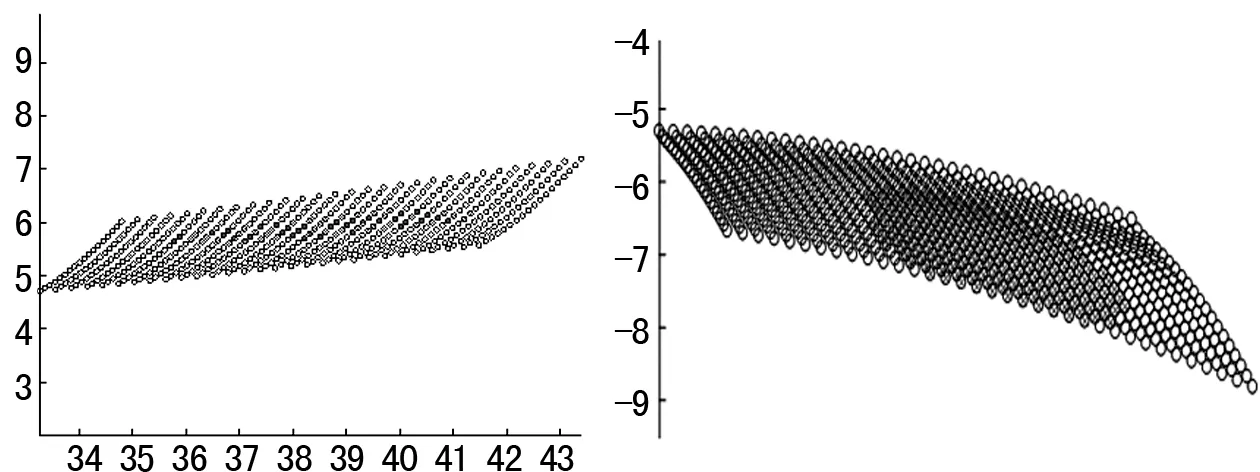
圖4 大輪接觸印痕仿真結果 圖5 小輪接觸印痕仿真結果

為了驗證仿真結果的準確性，將其與相同邊界條件下著色試驗接觸印痕結果進行對比，本文分別選取了大輪安裝距、小輪安裝距和軸交角3個變量的3組狀態進行正交試驗，共得到大小輪在27個裝配狀態下的仿真接觸印痕與試驗接觸印痕對比結果，小輪工作面在27個裝配狀態的接觸印痕對比如圖6～9所示，大輪工作面在27個裝配狀態的接觸印痕對比如圖10～13所示。

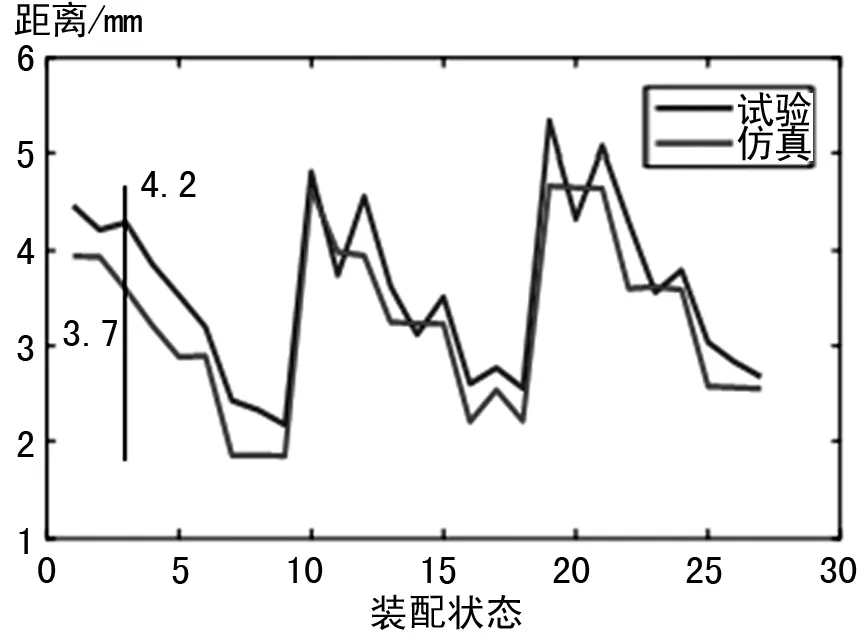
圖6 小輪工作面著色印痕離大端距離

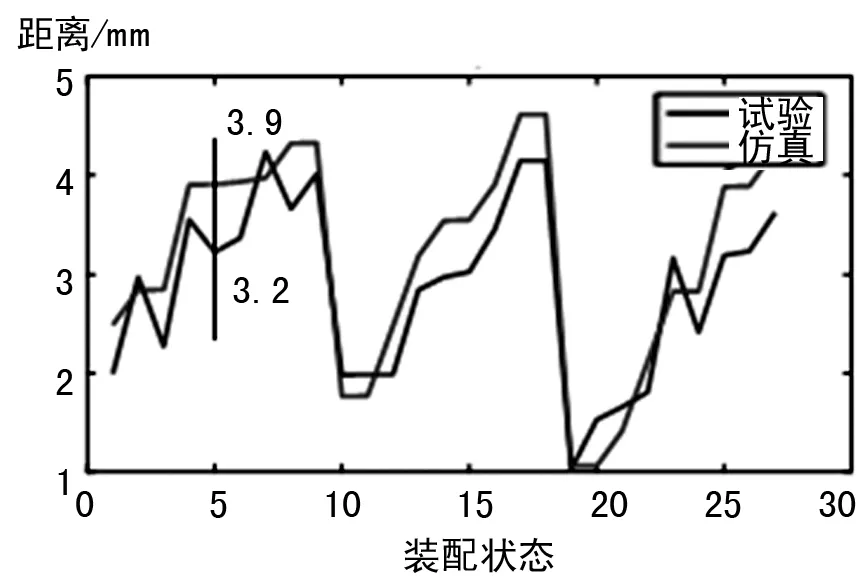
圖7 小輪工作面著色印痕離小端距離

圖8 小輪工作面著色印痕離齒頂距離

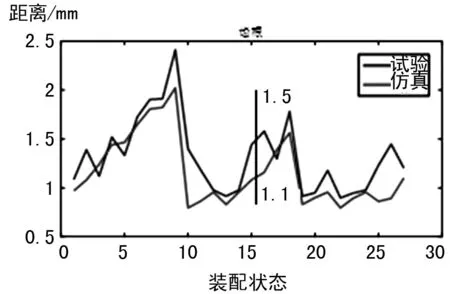
圖9 小輪工作面著色印痕離齒根距離

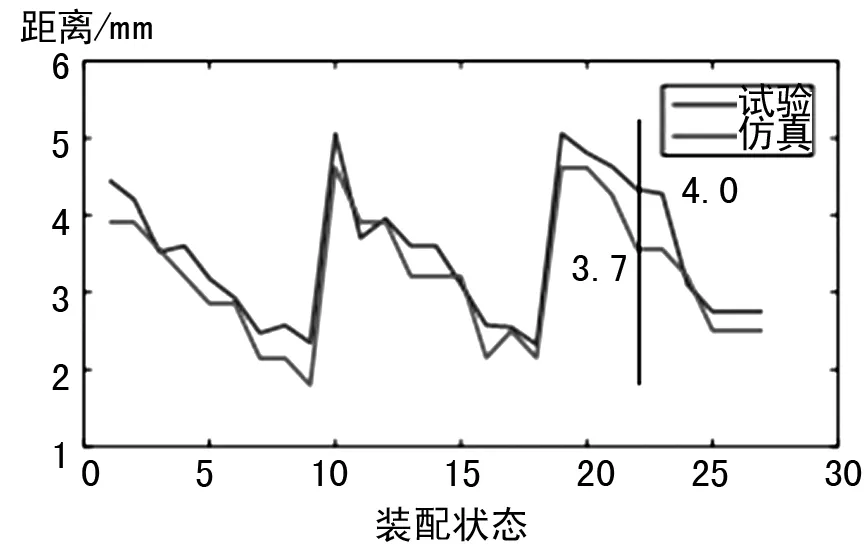
圖10 大輪工作面著色印痕離大端距離

圖11 大輪工作面著色印痕離小端距離

圖12 大輪工作面著色印痕離齒頂距離

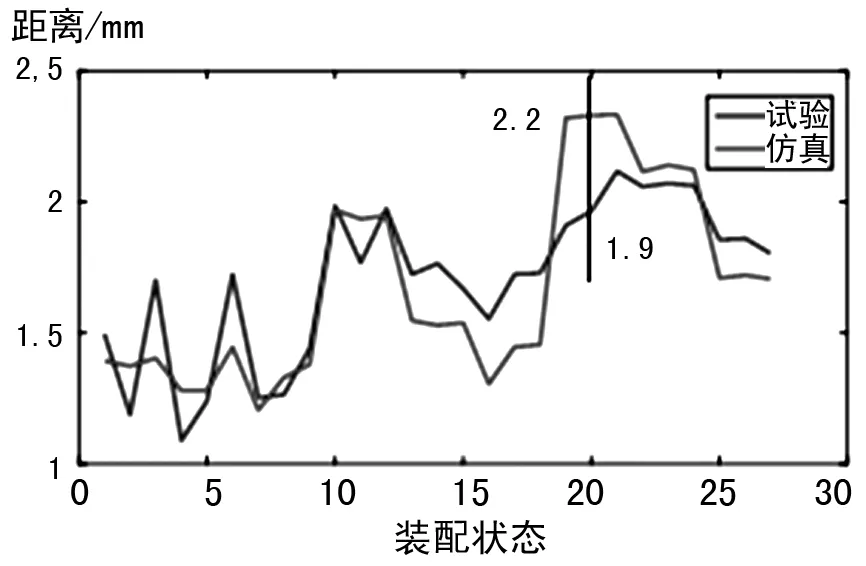
圖13 大輪工作面著色印痕離齒根距離

對比基于真實齒面的錐齒輪仿真分析結果及著色檢查結果可知：各裝配技術狀態下大、小輪仿真和試驗得到的接觸印痕形狀及位置基本一致，在齒寬方向上相對誤差最大值為12%，在齒高方向上相對誤差最大值為13%。

4 結 語

綜合考慮直齒錐齒輪加工參數、裝配誤差、加載變形，對直齒錐齒輪進行加載接觸分析，計算出實際工作狀態下的接觸印痕，與工廠著色試驗接觸印痕區域對比，在齒寬和齒高方向上的相對誤差均小于15%，認為此仿真方法正確可行，可為判定該直齒錐齒輪是否能滿足裝機要求提供理論指導，提前預知直齒錐齒輪接觸印痕并進行調整，提高航空發動機裝配效率。