LTE-U終端發射機信號EVM測量算法研究*

陳 章，安君帥，馮 晨，韓 娟

（1.南京熊貓漢達科技有限公司，江蘇 南京 210001；2.中國科學院計算技術研究所，北京 100190；3.中國科學院大學，北京 100049）

0 引 言

LTE-U協議在2013年被正式提出后，實現了授權載波與非授權載波的融合，極大地提高了通信系統的容量。LTE-U將授權頻段作為主載波，當感知到有空閑非授權頻段時將其獲取并作為輔載波，利用CA載波聚合技術將授權載波與非授權載波進行聚合，從而有效提升了系統性能。LTE-U對于無線資源是由基站集中控制分配，避免了終端的資源競爭，所以不會隨著用戶的增多而發生數據碰撞的現象，可大幅度提升資源利用率。LTE-U得以迅速發展與推廣，成為目前4G向5G通信推進的堅實基礎。

EVM是用來表征系統調制質量的參數，是在一個給定時刻的理想信號與實際發射信號的向量差，可直觀反映通信質量與發射機性能的好壞[1]。EVM的優點主要包括：①EVM相對于眼圖或誤比特率（Bit Error Ratio，BER）等其他測量指標，可以更直觀地反映出信號的質量；②EVM相對于眼圖或BER等其他測量指標的測量速度更快；③EVM可與信噪比（Signal to noise ratio，SNR）建立直接的關系，因此可以更全面地反映信號質量的好壞與環境噪聲之間的聯系[2]。

通信中，由于通道的非線性失真、終端各射頻模塊質量不能達到理想情況、多種信道噪聲以及環境影響等，都會造成接收端接收到的實際數字調制信號與理想調制信號在幅度、相位及頻率上存在一定的差異。這些差異會導致星座圖上理想信號與接收到的信號星座點不重合，導致EVM計算存在很大的偏差[3]。所以，在進行EVM測量前，準確定時同步與消除頻偏、相偏和I/Q不平衡參數的影響是測試EVM的關鍵。針對定時同步，文獻[4-5]提出了基于導頻的同步算法，而文獻[2]提出了最小幅度方差法；針對頻偏估計，文獻[6-7]提出了時域頻偏算法，文獻[8]提出了基于導頻的FFT-CZT頻偏估計算法；針對I/Q不平衡參數估計，文獻[1]提出了二元線性擬合算法。本文在研究LTE-U射頻一致性測試系統的開發過程中，結合LTE-U協議提出了一種有效的EVM值計算方法，給出了PUSCH信道EVM測試過程的仿真分析。

1 測量方案及算法流程

EVM是誤差矢量與參考矢量之間建立的一種關系，結果表示為誤差矢量幅度相對于參考矢量幅度之間的百分比形式。本文研究PUSCH信道下EVM測量，相關位置如圖1所示。其中，R為理論的理想參考信號抽取位置，Z為被測接收信號的位置。

圖1中上線框內為終端調制信號的發送過程，即將數字信號通過比特級處理（CRC添加、碼塊分段、Turbo編碼、速率匹配）生成調制符號，經傳輸預編碼——離散傅里葉變換（Density Functional Theory，DFT）和SC-FDMA符號生成——快速傅里葉反變換（Inverse Fast Fourier Transform，IFFT），生成上行基帶信號用于發送[9]。由于發射機模擬元件的精度限制，仿真時人為加入了高斯白噪聲等干擾條件。圖1中下線框內為終端測試儀內進行EVM計算的過程，主要是生成上行基帶信號的逆過程，但在FFT與IDFT變換前，需加入射頻信號糾正過程（包括定時同步、頻偏估計、相偏估計、I/Q不平衡參數估計等步驟）[3]。

圖1 EVM的測試點位置

2 EVM測量算法

本文提出的EVM測量算法運算快、易于實現，適用于針對LTE-U協議上行業務信道EVM測量的具體實現。具體EVM測量算法流程中，關鍵功能模塊主要包括：①定時同步，用于搜索同步樣點，保證后續測量能在精確獲取信號的基礎上進行；②頻偏、相偏的估計補償，即估計并補償信號的頻偏、相偏，以減小待測信號載波間干擾；③I/Q不平衡參數估計和補償面積估計并補償I/Q路不平衡的增益、相位以及直流偏移。

2.1 定時同步算法

定時同步算法是研究如何從幀數據流中找到準確起始位置的算法，對后續的EVM測量的精度有一定影響。因此，需要在進行測量前通過同步算法精確定位幀數據流中的起始位置。

經研究，本文采用基于導頻的同步算法，相較最小幅度方差法，該算法計算量小，可極大減少運算時間，且易于實現。后續仿真表明，基于該算法的定時同步可準確穩定地精確到相應的符號，足以滿足基于LTE-U協議PUSCH信道的EVM計算實現的需求。

基于導頻的同步算法是將本地用作參考的導頻序列與接收到的信號進行滑動相關，即將本地導頻序列與接收到的信號滑動共軛相乘，計算相關結果并搜索出最大值，其對應的點即為接收信號的同步點[3]。具體算法原理如下[10]：

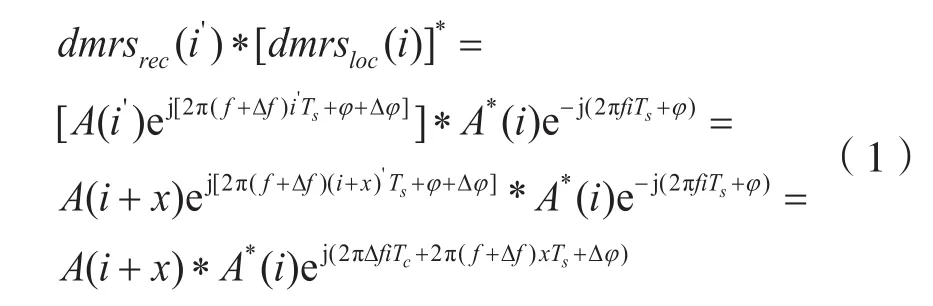
其中，dmrsrec(i′)代表接收導頻序列第i個符號，dmrsloc(i′)代表本地導頻序列第i個符號。A(i)為復數幅度；i為符號位置；Ts為符號周期，Δf為頻偏；Δφ為相偏。由導頻序列的相關性，可知：

易得當x=0時，其值最大。因此，信號同步是利用導頻序列具有很好的自相關特性搜索出相關幅值最大點對應的位置，即可作為接收信號同步點的位置。

2.2 頻偏相偏估計算法

在無線通信系統中，由于多普勒效應以及發送機和接收機的晶振穩定度不夠等原因，導致接收信號產生頻偏與相偏，進而使子載波之間產生干擾。頻偏與相偏估計算法是EVM測試的基礎，它的精度決定了最終EVM測試的精度[11]。目前，頻偏估計算法主要有典型時域頻偏估計算法和基于導頻的頻偏估計算法。

典型時域頻偏估計算法即將接收到已同步的導頻信號序列（DMRS解調參考信號）與本地標準導頻序列共軛對位相乘得到相關幅度，并找出其中最大值Peak，計算頻偏[7]：

其中，i為符號位置。但是，這種算法的精度不高。

基于導頻的頻偏估計算法利用LTE-U協議中1個子幀中含有2個DMRS符號的特點，通過計算2個DMRS符號之間的相位差和符號位置差對頻偏進行估計。由于這2個符號在時域上相距一個時隙（0.5 ms），比1個符號所占的時間大大增多，因此可以更加準確地計算頻偏值[8]。然而，這種方法犧牲了估計范圍，求取的相位差值θ必須保證在-π到π之間，否則會造成相位模糊。

本文將兩種算法結合，可快速精確地估計出頻偏和相偏值。基本流程為：先用典型時域頻偏估計算法進行第一頻偏估計，結果記為粗頻偏；根據估計的粗頻偏進行頻偏修正，再用基于導頻的頻偏估計算法估計細頻偏；最終頻偏結果即為粗頻偏與細頻偏的和值。

具體過程如下。

步驟1：尋找導頻信號序列同步得到的相關幅度的最大值Peak計算粗頻偏，如式（3）所示。

步驟2：對接收到的原解調參考信號序列進行粗頻偏補償，再將1個子幀中的2段DMRS符號共軛相乘計算細頻偏，得到[5]：

其中，i1和i2分別代表2段DMRS的樣點位置。

步驟3：將粗頻偏Δf1與細頻偏Δf2相加，即為估計頻偏Δf的精確結果。

步驟4：對接收到的信號精確的頻偏修正后進行相偏估計和修正，得到：

其中，dmrscor是頻偏修正后的DMRS序列，dmrsloc是本地標準DMRS序列。

2.3 I/Q不平衡參數估計算法

I/Q不平衡參數包括I/Q幅度不平衡、I/Q相位不平衡以及I/Q信號偏移。理想的I/Q兩路數據是正交對稱的，即幅度比為1，相位差為π/2，且不含有直流偏移。但是，由于工程中的誤差會導致I/Q參數不平衡[12]。

由發射機I/Q不平衡模型可知，接收端接收到的信號為：

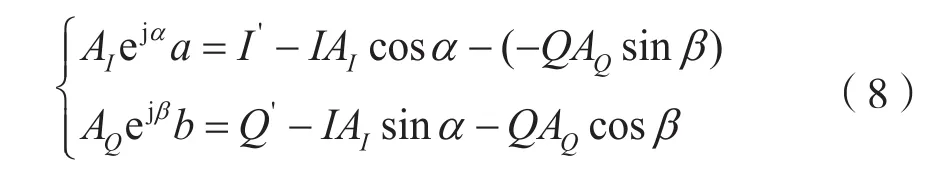
其中，I′為接收信號的I路數據；Q′為接收信號的Q路數據；AI為I路增益；AQ為Q路增益；α為I路相位不平衡；β為Q路相位不平衡；a為I路直流偏移；b為Q路直流偏移。

由于I/Q兩路數據為正交關系，即兩個自變量I/Q之間不會存在線性關系，所以本文用二元線性擬合法對I/Q不平衡參數進行求解[4]。經研究，二元線性擬合法算法簡單、容易實現且輸出穩定精確。

二元線性回歸模為：

再利用接收到的解調參考信號（Demodulation Reference Signal，DMRS）與本地標準DMRS序列根據二元線性擬合法，便可解出I/Q不平衡參數。

3 仿真結果與性能分析

當輸入信號的SNR較大（SNR＞10 dB）時，即m(n)遠遠大于e(n)時，m(n)可以約等于r(n)，此時便可推導出EVM與SNR的對應關系：

根據不同的信號質量，即不同的SNR進行仿真，其中具體仿真所設條件參數如表1所示。

表1 EVM算法仿真驗證條件參數表

圖2展示了不同SNR條件下，實際測量的EVM與SNR關系曲線以及其理想關系曲線的對比結果。可以得出：隨著SNR（信噪比）的增加，計算的EVM值在減小。當SNR為1 dB到10 dB時，實際測量結果與理想值之間存在較大差值，這是由于此時信噪比過低，即信號不能遠遠大于噪聲所導致的理想值估計不夠精確的原因。在LTE-U系統中，QPSK調制方式的EVM最小值要求為17.5%[13]，則由式（11）便可推導出QPSK調制方式下的EVM信噪比門限值為15.14 dB。由圖2可知：本文提出的EVM算法的信噪比門限值為12.8 dB，與理論值誤差不超過2.34 dB。門限值內的相對誤差不大于1%，即能夠精確完成EVM計算。

圖2 EVM與SNR關系曲線

為了驗證本文提出的EVM測量方案的正確性，使得理想信號通過信道信噪比為15 dB。表2是通過10次仿真取平均得出PUSCH_QPSK的EVM為13.51%，與理論結果誤差不超過4.5%，并對EVM仿真測量值的合成不確定度進行研究，合成不確定度在0.079 30范圍內，說明算法足夠穩定。合成不確定度定義式：

其中s為標準差。

表2 EVM測量結果表

4 結 語

本文以PUSCH信道的EVM測試為例，分析了LTE-U系統的EVM測量實現算法。該算法通過準確的定時同步、精確的頻偏估計、初始相位估計以及I/Q不平衡參數的測量算法，可以快速、精確地測量LTE-U系統PUSCH信道的EVM指標。仿真和實驗結果表明，該算法易于實現，測量精度及可靠性較高，具有一定的實用性和指導意義。