基于T-ACO算法的旅行商問題求解優化研究

費騰 趙斌 黃俊東 劉澤田

摘 ?要：為了有效求解旅行商問題，本文提出了一種基于T分布的改進蟻群算法。針對基本蟻群算法易陷入局部最優、尋優精度低等缺陷，在優化過程中，在信息素更新原則上，引入T分布，有益于基本蟻群算法彌補其不足。在基本蟻群算法中增加了信息素的突變，使得螞蟻群的多樣性提高，從而跳出局部最優的限制。與此同時，T-ACO算法在旅行商問題搜尋精度與收斂速度方面也得到了提高。對T-ACO求解旅行商問題的性能進行了實驗仿真，實驗分析表明，T-ACO算法有更好的尋優能力。

關鍵詞：T分布;蟻群算法;旅行商問題;優化

中圖分類號：TP391.9 ? ? 文獻標識碼：A

1 ? 引言（Introduction）

旅行商問題由Ramser B博士在1959年根據車輛路徑的選擇問題提出，該問題屬于數學領域的經典問題。TSP問題的實質為一個供貨商為不同的需求客戶送貨，要求配送路徑不可以重復的情況下，選擇路程最短的路徑作為最終的配送路徑[1]。眾多學者已經證明了TSP問題是一個經典的NP-hard問題。因此，近些年來，學者都將研究的重點放在求解TSP問題的算法設計上。目前解決TSP問題的方法大致分為兩種，一種是包括分支定界法、線性規劃法和動態規劃法在內的啟發式搜索算法[2]，另外一種是包括模擬退火算法[3]、禁忌搜索算法[4]、遺傳算法[5]、蟻群算法[6]、遺傳算法[7]，以及粒子群算法[8]等的人工智能優化算法。由于現在有眾多實際問題可以轉化為TSP模型[9]，因而TSP問題諸如電網規劃[10]、網絡優化[11]、交通運輸[12]、物流配送[13]等重要領域都有著廣泛的應用。

為了有效求解旅行商問題，本文提出了一種基于T分布的改進蟻群算法。針對基本蟻群算法易陷入局部最優、尋優精度低等缺陷，在優化過程中，在信息素更新原則上，引入T分布，有益于基本蟻群算法彌補其不足。在基本蟻群算法中增加了信息素的突變，使得螞蟻群的多樣性提高，從而跳出局部最優的限制。與此同時，T-ACO算法在旅行商問題搜尋精度與收斂速度方面也得到了提高。對T-ACO求解旅行商問題的性能進行了實驗仿真，實驗分析表明，T-ACO算法有更好的尋優能力。

2 ? 旅行商問題（Traveling salesman problem）

旅行商問題可以簡單描述為在給定的個城市里，每個城市只經過一次，然后回到出發點，找出使該回路最短的路徑的問題。TSP問題的數學模型如下[14]：

式中，表示指定的點集;表示邊集;表示賦值圖;表示點到點的距離;表示點在回路路徑上，表示不在回路路徑上;表示的子圖，對應的約束條件保證沒有任何子回路解的產生。旅行商問題的目的是為了獲得一個最優回路，在該回路上，除了起點之外的每一個點只能經過一次。

3 ? T-ACO算法（T-ACO algorithm）

3.1 ? T分布

T分布又被稱為學生分布，威廉·戈塞于1908年[15]首先推導發表，自由度為的T分布的概率密度函數為：

根據式（5）可以卡看出，T分布的分布曲線與參數自由度有關。若越小，則T分布曲線就越平坦。若分布曲線中間部分越平坦，則多對應兩側的尾部的曲線就會凸起的越高。這就存在兩種特殊的情況，一種情況為時，T分布曲線為柯西分布曲線。另外一種情況為時，T分布曲線為高斯分布曲線。T分布變異恰好融合了柯西分布變異和高斯分布變異的特點，通過不斷改變自由度參數的值可以獲得不同變異幅度。

3.2 ? 基于T分布的蟻群算法

基本蟻群算法是對螞蟻的生物學原理進行模擬后的一種人工智能優化算法。基本蟻群算法根據信息素遺留的多少來判定選擇的路徑，路徑上遺留的信息素越多，則該路徑被選擇的概率就越大。

基本蟻群算法易陷入局部最優、尋優精度低等缺陷，為了克服上述缺陷，將T分布引入信息素更新中。由于T分布具有較好的擾動作用，使得群體多樣性增加，因此能夠提高算法的收斂速度，且不受局部最優的限制，增加尋得全局最優解概率。

為了提高收斂速度，可事先確定一個閾值，以避免螞蟻周游一次后，較差解所帶來的無效搜索。同時，為避免蟻群算法陷入局部最小，在調整信息素時，引入T分布，用以跳出局部最小點。改進后的各條路徑上的信息素調整為

其中，表示信息素揮發程度，;表示所有螞蟻在節點與節點間的信息素濃度的總和;表示第只螞蟻在節點和節點之間路徑上釋放的信息素濃度;為螞蟻循環一次釋放的信息素總量，的大小對算法的收斂速度有影響;為第只螞蟻走過的路徑長度;為T分布變量。

3.3 ? 求解步驟

步驟1 參數初始化，包括、、及等蟻群算法參數以及T分布變異的特征參數。

步驟2 令，為迭代次數，將只螞蟻隨機放在座城市。

步驟3 根據式（9）計算螞蟻的轉移概率，選擇并移動到下一個城市，同時將加入到中。

其中，為信息素重要程度因子，反映螞蟻間的協作能力;為啟發函數重要程度因子，反映螞蟻對于啟發信息的重視程度;為啟發函數表示螞蟻從節點轉移到節點的期望，，表示兩點間的距離，為螞蟻待訪問的節點集合。

步驟4 是否滿。若為否，回到步驟3，否則，繼續步驟4。

步驟5 按式（6）—式（8）進行T分布信息素的全局更新。

步驟6 判斷是否，若為是，重復步驟3—步驟6，否則，結束迭代，輸出最優解。

4 ? 實驗仿真（Experimental simulation）

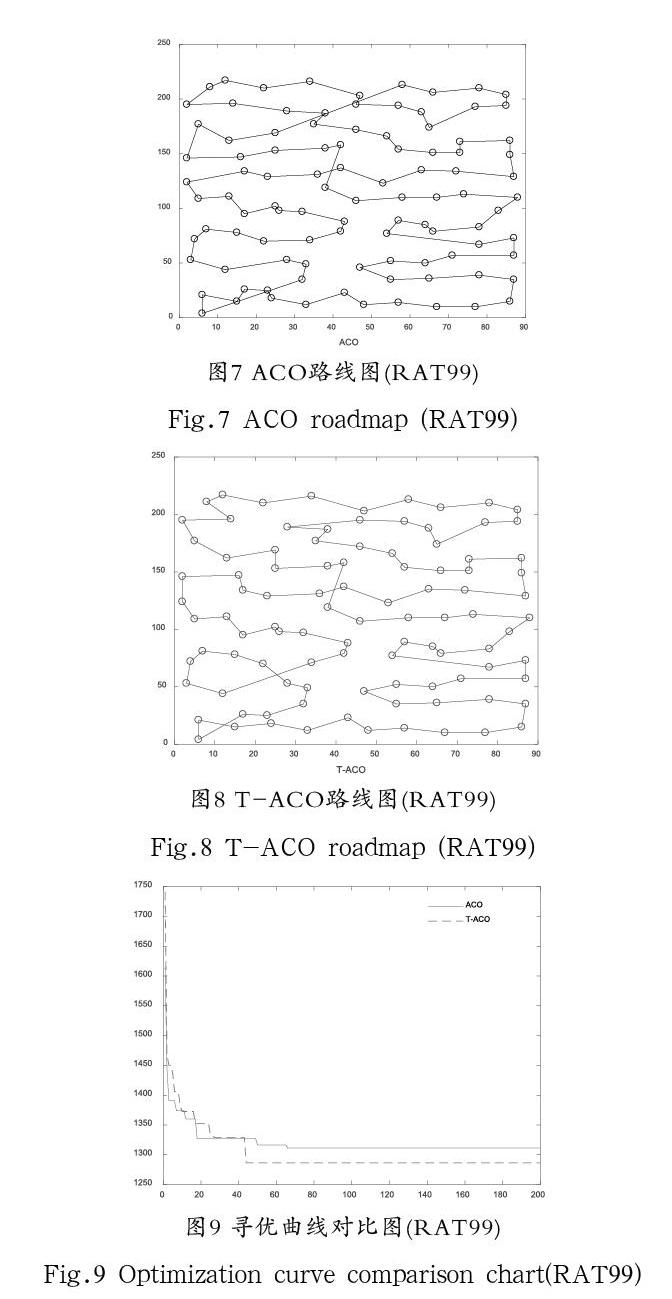
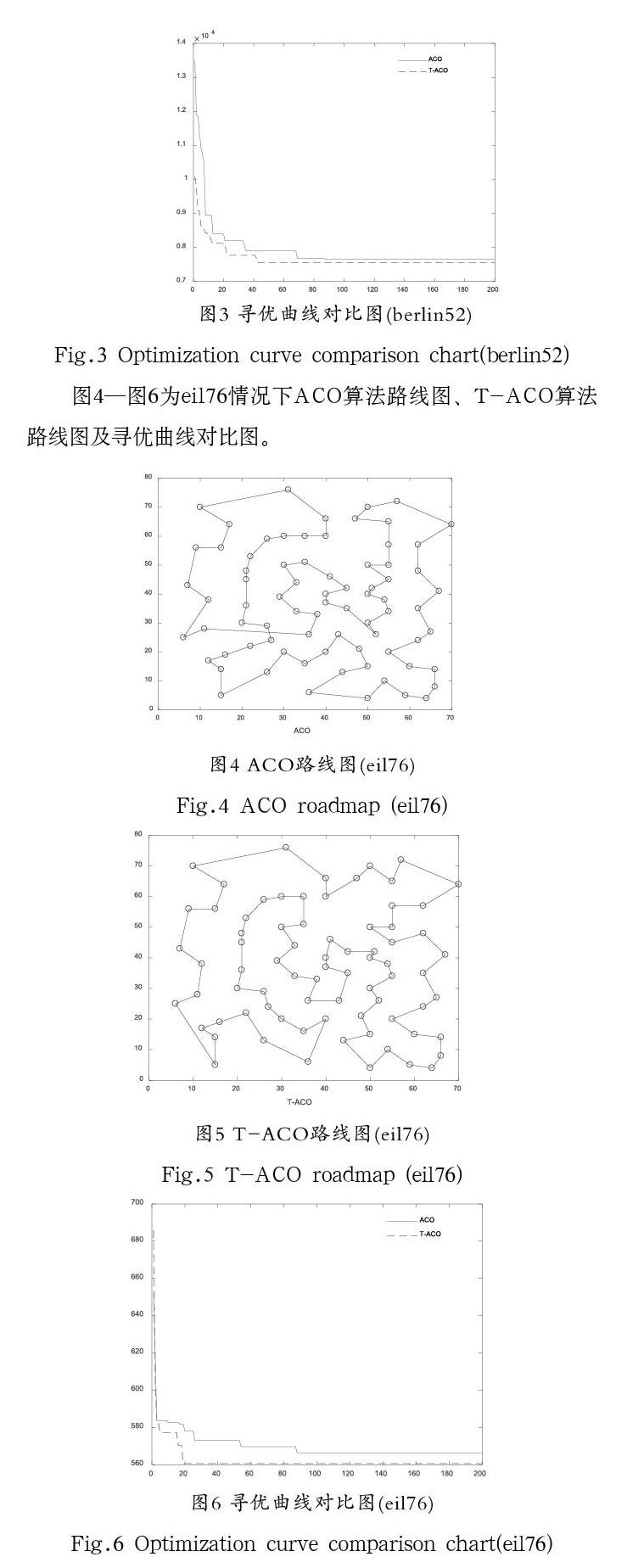
為了驗證算法的有效性，利用TSPLIB標準庫中的berlin52、eil76及RAT99三個測試集進行算法性能測試[16]。設置最大迭代次數，信息素重要程度因子，啟發函數重要程度因子，信息素全局揮發因子，信息素釋放總量。表1為在重復實驗30次的情況下，ACO算法及T-ACO算法在三個測試集所獲得最優解、最差解和平均值。表2為ACO算法及T-ACO算法在三個測試集所獲得成功率、平均收斂代數及標準差。

從上述測試可以看出：在尋優能力方面，T-ACO算法在最優解、最差解及平均值都優于ACO。在收斂速度方面，T-ACO的平均收斂代數少于ACO。在穩定性方面，T-ACO標準差小于ACO。由此可以看出，T-ACO算法相對于ACO算法更有效。

5 ? 結論（Conclusion）

為了彌補基本蟻群算法的不足，將T分布引入到蟻群算法中，提出改進的蟻群算法（T-ACO）。利用改進的蟻群算法求解旅行商問題，并將其結果與基本蟻群算法進行了對比對比發現，改進的蟻群算法在求解旅行商問題上比基本蟻群算法更具有優越性，具有更好的收斂性和更高的收斂精度。本文的研究仍存在一些不足，解決旅行商問題時，使用的對比算法較少，這是后續研究需要加入的部分。

參考文獻（References）

[1] 王凌.智能優化算法及其應用[M].北京：清華出版社，2001：

218-222.

[2] 李軍民，林淑飛，高讓禮.用混合遺傳算法求解多目標問題TSP問題[J].西安科技大學學報，2006，26（4）：515-518.

[3] HE Qing，WU Yi-Le，XU Tong-Wei.Application of improved genetic simulated annealing algorithm in TSP optimization[J].Control and Decision，2018（2）：219-225.

[4]王宏斌，劉娜.基于優先權編碼的改進禁忌搜索算法求解TSP問題[J].物流科技，2017，40（6）：29-32.

[5] 施泰龍，鄭悠，王蔚，等.引入外來種群的禁忌遺傳混合算法求解TSP問題[J].寧波工程學院學報，2017，29（3）：20-25.

[6] 許凱波，魯海燕，程畢蕓，等.求解TSP的改進信息素二次更新與局部優化蟻群算法[J].計算機應用，2017，37（6）：1686-1691.

[7] 張勇，高鑫鑫，王昱潔.基于SFLA-GA混合算法求解時間最優的旅行商問題[J].電子與信息學報，2018，40（2）：363-370.

[8] 裴皓晨，婁淵勝，葉楓，等.一種求解旅行商問題的改進混合粒子群算法[J].計算機與數字工程，2018，46（2）：218-235.

[9] Cavdar B，Sokol J.A distribution-free TSP tour length estimation model for random graphs[J].European Journal of Operational Research，2015，243（2）：588-598.

[10] 王賽一，王成山.遺傳禁忌混合算法及其在電網規劃中的應用[J].電力系統自動化，2004，28（20）：43-46.

[11] 沐士光.遺傳算法在網絡優化問題中的研究與應用[J].計算機仿真，2010，27（5）：128-131.

[12] 鐘石泉，杜綱.基于核心路徑禁忌算法的開放式車輛路徑問題研究[J].計算機集成制造系統，2007，13（4）：827-832.

[13] 王華東，李巍.粒子群算法的物流配送路徑優化研究[J].計算機仿真，2012，29（5）：243-246.

[14] 鄧義成，任聲策，殷旅江.基于改進果蠅算法的旅行商問題[J].蘭州理工大學學報，2016，42（4）：109-113.

[15] 茆詩松.概率論與數理統計教程[M].北京：高等教育出版社，2004：22-28.

[16]TSPLIB[EB/OL].http：//comopt.ifi.uni-heidelberg.de/software/TSPLIB95/，2016-12-10.

作者簡介：

費 ? 騰（1983-），女，博士，副教授.研究領域：智能計算與群智能算法.

趙 ? 斌（1983-），男，本科，講師.研究領域：算法研究.

黃俊東（1999-），男，本科生.研究領域：自動化設計.

劉澤田（1999-），男，本科生.研究領域：智能算法.