差分組合目標定位的艦炮對海射擊檢靶方法

徐義桂，陳維義

(海軍工程大學 兵器工程學院，武漢 430033)

水面艦艇艦炮武器系統執行對海射擊訓練任務時，目前常采用艦載雷達、光電跟蹤儀等設備完成海上檢靶任務。但是艦載雷達對海上目標探測時，存在一定的不足：易受到海雜波和多路徑的影響，探測性能低；有時其無法將目標回波從復雜背景回波中分辨出來；對炸點海水柱回波無自動識別功能且顯示效果不清晰，等等。而艦載光電跟蹤儀探測時又易受船體的搖擺影響，光電平臺不易穩定。這樣就造成了炸點海水柱測不到、測不準、檢靶效率低以及檢靶過程繁瑣等問題，不利于艦炮射擊效果的評定和編隊射擊訓練工作的組織。

當前，隨著無人機目標定位技術的不斷發展，可對海上目標進行視頻實時偵察定位，具備實時性強、效率高、分辨率高、造價低及使用便利等優點，可用于解決上述問題。通過查閱相關文獻發現，周前飛[1]、徐誠[2]、蔡明兵[3]等提出了基于機載光電平臺的多目標定位算法，可以同時完成對多個目標實時定位，具備目標定位效率高、實時性強及工程應用性強等優異特性，但是，由于鏡頭畸變、傳感器測量誤差等因素的影響，導致目標定位精度不佳；張輝[4]、樊邦奎[5]等提出了無人機空間三點距離交會定位的方法，由于該方法在一定程度上減少了無人機姿態角、光軸穩定轉臺角度等測量誤差對目標定位的不良影響，目標定位精度較高，但是該方法只能對單點目標進行定位。通過分析無人機海上檢靶的過程可知，在執行檢靶任務時涉及到對海上靶標(理論上的靜止靶標)和炸點海水柱同時定位過程，且測量精度要求盡可能高。因此，本研究在上述前人研究的兩種目標定位技術的基礎上進行融合改進，提出了差分組合的目標定位方法。

1 差分組合定位原理和模型解算過程

1.1 差分組合定位原理

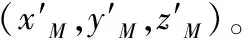
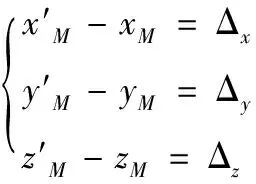
(1)

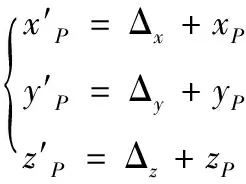
(2)

1.2 模型解算過程

可選用具備垂直起降的固定翼無人機(如，KC3400型無人機)，如圖1所示，其攜帶相應的載荷后(電視攝像機、激光測距儀等)，經艦艇編隊釋放并前出至指定區域進行工作。無人機差分組合定位的艦炮射擊檢靶模型解算過程如圖2所示。

圖1 KC3400型垂直起降固定翼無人機

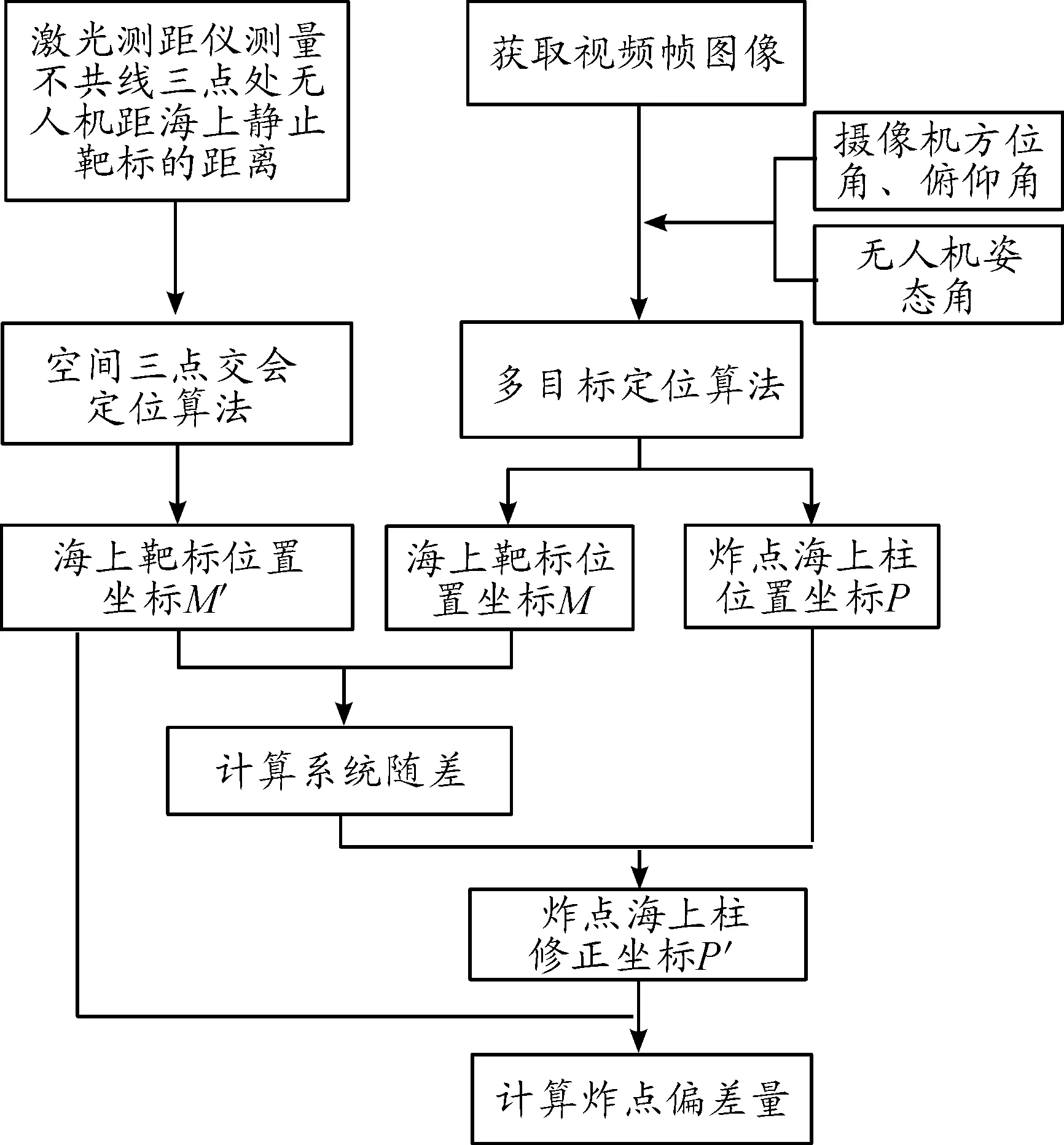
圖2 模型解算過程框圖

2 炸點海水柱的偏差量測量

在艦炮對海射擊訓練過程中，通過無人機完成檢靶任務的關鍵是要完成無人機對海面靜止靶標和炸點海水柱的高精度定位，然后才能計算出炸點與靶標之間的偏差量。無人機多目標定位算法，是通過一次測量達到同時多點定位的目的，具體過程為：首先建立坐標轉換空間坐標系及確定坐標之間的轉換關系，然后根據某時刻目標定位過程中的海上靶標、炸點海水柱及它們在像片中的幾何位置關系，并融合無人機姿態角、攝像機轉角、攝像機焦距等參數，推導出所拍攝圖像中任一點在攝像機坐標系中的坐標，接著通過齊次坐標轉換解算得到海上靶標和炸點海水柱在大地空間直角坐標系下的位置坐標，即完成多目標定位過程[1-3]。空間三點交會目標定位算法，是通過對海上靶標實施跟蹤過程中，在三個不共線的位置點分別進行采樣，然后對采樣后的數據進行空間交會解算并通過坐標轉換得到海上靶標在大地空間直角坐標系下位置坐標的定位算法，特別適合針對單一目標進行重點偵察定位[4-5]。利用差分組合定位原理對炸點海水柱的位置坐標進行修正，以達到減少系統隨機誤差對定位結果影響的目的。最終在得到海上靶標位置坐標和炸點海水柱的修正位置坐標后，計算其兩者間的距離(又稱之為炸點海水柱偏差量)。

2.1 多目標定位算法

2.1.1坐標系定義

多目標定位算法涉及六個空間坐標系，如圖3所示，分別定義為[2,6-7]：① 大地坐標系C，在大地坐標系中任一點的坐標以緯度B、經度L和大地高H表示，如圖3(a)所示；② 大地空間直角坐標系E：與大地坐標系定義完全相同，但在大地空間直角坐標系中任意一點的坐標是以直角坐標的形式表示，如圖3(a)所示；③ 載體地理坐標系G，即為“東北天坐標系 ”，如圖3(a)所示；④ 載體機體坐標系B，當載體機體坐標系相對載體地理坐標系的三軸姿態角為0°時，其三軸指向與載體地理坐標系三軸指向重合，設φ(偏航角)、ω(橫滾角)、θ(俯仰角)分別為繞Zb、Yb、Xb軸旋轉的轉角，如圖3(b)所示；⑤ 攝像機坐標系S，當攝像機在初始位置時，Zs軸指向載機機頭，Ys軸指向機體正下方，Xs軸指向載機右翼的方向，三軸構成右手坐標系，其中光軸旋轉角為方位角α和高低角β，如圖3(c)所示；⑥ 圖像坐標系W，如圖3(d)所示。

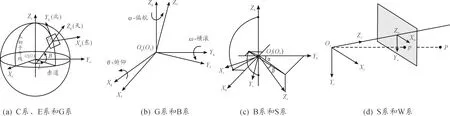
圖3 各坐標系定義

2.1.2坐標轉換過程

在圖3中，建立了多目標定位模型中所用的空間坐標系，設目標像點在W系下的坐標為(xw,yw)，目標分別在S系、B系、G系和E系下坐標為(xs,ys,zs)、(xb,yb,zb)、(xg,yg,zg)和(xe,ye,ze)，目標在C系下的坐標為(B,L,H)。

1)根據某時刻目標的像點在攝像機屏幕坐標(即圖像坐標系下的坐標)，由三角形相似原理可得目標P在攝像機坐標系下的xs、ys坐標，zs可由本文2.1.3節求解得到：

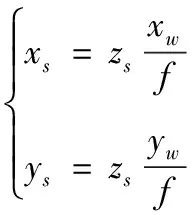
(3)

其中f為攝像機的焦距。

2)根據齊次坐標轉換法，可用四階矩陣來表示坐標的旋轉、平移、放大或縮小等[8]。借助此種方法，將目標在攝像機坐標系下的坐標轉換為在大地空間直角坐標系下的齊次坐標，計算公式為：

(4)

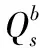
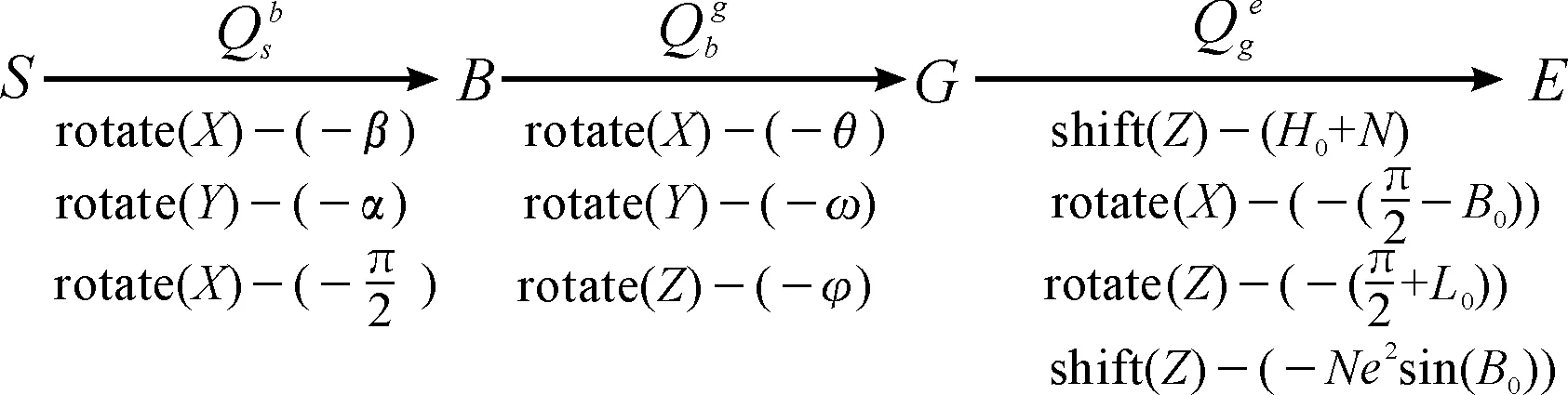
α、β為攝像機光軸的方位角、俯仰角，φ、ω、θ為無人機偏航角、橫滾角、俯仰角，B0、L0、H0為無人機某時刻所處的經度、緯度、高度，N為某處WGS-84橢球卯酉圈曲率半徑，e為WGS-84橢球的第一偏心率。

3)由大地測量學基礎知識可知[7]，大地坐標系與大地空間直角坐標系之間的坐標轉換公式為：

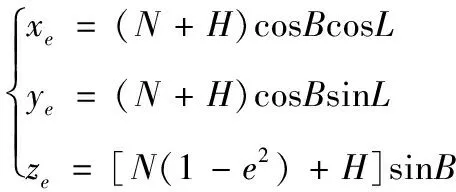
(5)

(6)

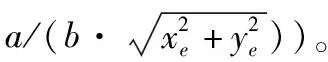
2.1.3多目標定位模型

圖4所示為無人機定位過程中海上靶標、炸點海水柱和它們在像片中像點的幾何關系模型，M為海上靜止靶標，P為炸點海水柱，m、p為它們在像片中的像點，T1為海平面，T2為圖像平面。在無人機對海上靶標定位過程中，利用光電跟蹤器產生標志框套住靶標，并控制光軸穩定轉臺轉動將目標始終鎖定在攝像機視場中心。待艦炮射擊后，攝像機視場內炸點海水柱出現瞬間，鎖定該幀圖像并輸出無人機遙測參數。

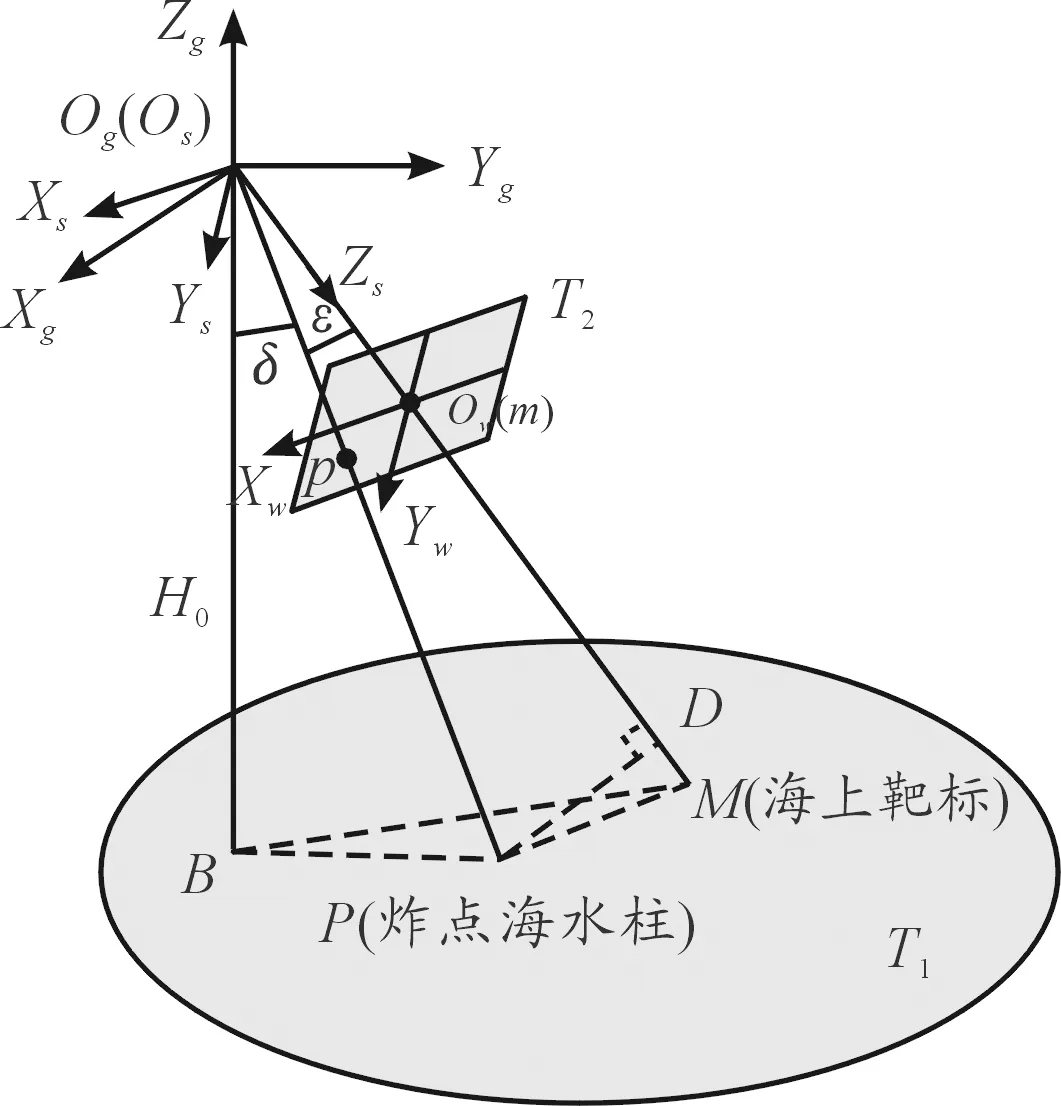
圖4 目標、炸點和像點的成像幾何關系模型

1)海上靶標的位置定位

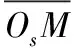
(7)

2)炸點海水柱的位置定位

在某一時刻無人機搭載的攝像機獲得的幀圖像中，炸點海水柱像點p分別在圖像坐標系和攝像機坐標系下的坐標為(xwp,ywp)、(xwp,ywp,f)，攝像機的焦距為f，且設OsP與OsM的夾角為ε，則：

(8)

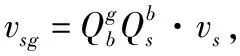
(9)

根據圖5的幾何關系可知：

(10)

則炸點海水柱在攝像機坐標系中的Zs軸坐標值為：

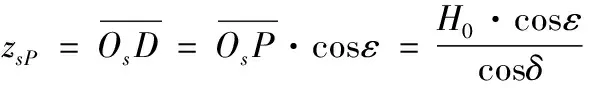
(11)

又將式(8)代入式(11)便可得：

(12)

再將式(12)代入式(3)可得xsp和ysp：

(13)

結合上述各式可得，炸點海水柱在攝像機坐標系下的齊次坐標值為tsP=[xsP,ysP,zsP,1]T，最后由式(4)的齊次坐標轉換可得炸點海水柱在大地空間直角坐標系中的齊次坐標teP=[xeP,yeP,zeP,1]T。

2.2 空間三點交會定位算法

圖5所示為當無人機偵察到海上靶標后，光電跟蹤器通過標志框套住目標，無人機沿其飛行軌跡在海上靶標上空附近區域飛行，并在其的航跡三點處分別進行一次激光測距，設激光測距值為R1，R2，R3；同時輸出無人機的位置坐標，分別為(x1,y1,z1)、(x2,y2,z2)、(x3,y3,z3)，則：

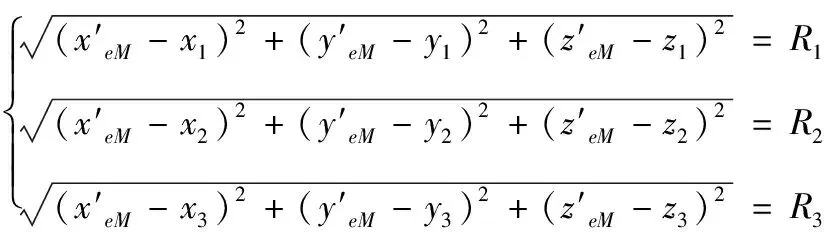
(14)

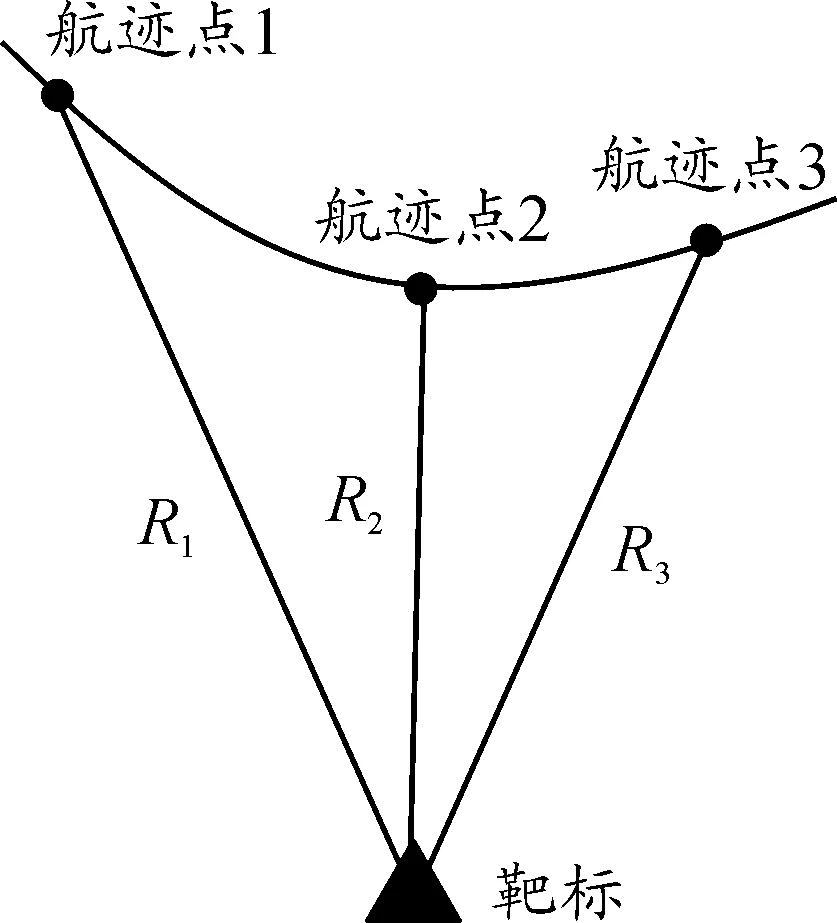
圖5 無人空間三點交會定位示意圖

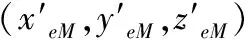
(15)

3 炸點海水柱偏差量測量誤差分析

3.1 蒙特卡洛仿真實驗

誤差分析是衡量炸點海水柱偏差量測量模型優劣的重要環節。在借助無人機平臺進行炸點海水柱偏差量測量過程中，影響炸點海水柱偏差量測量結果的因素很多，主要包括：GPS測量誤差、導航系統的姿態角測量誤差、載荷傳感器測量誤差及像片中像點坐標測量誤差等。由概率論知識可知，這些測量誤差近似的服從正態分布，因此可假設參數測量誤差Δx服從的分布為[9]：

Δx～N(0,σ)

故可利用模特卡羅法建立誤差傳遞模型：

ΔY=G(x1+Δx1,…,xn+Δxn)-G(x1,…,xn)

(16)

其中：xi為各參數的名義值；Δxi為各參數的測量誤差，G為相關模型計算過程。

為了分析本文炸點海水柱偏差量測量模型的誤差特性，可采用蒙特卡洛模擬統計實驗的方法分析模型的誤差特性。其中，可根據各傳感器設備技術手冊上提供的最大標定誤差作為模擬過程中各測量誤差正態分布的均方差值[10-11]，如表1所示。于是通過蒙特卡洛方法可統計出炸點海水柱偏差量誤差的均方差，具體步驟如圖6所示。

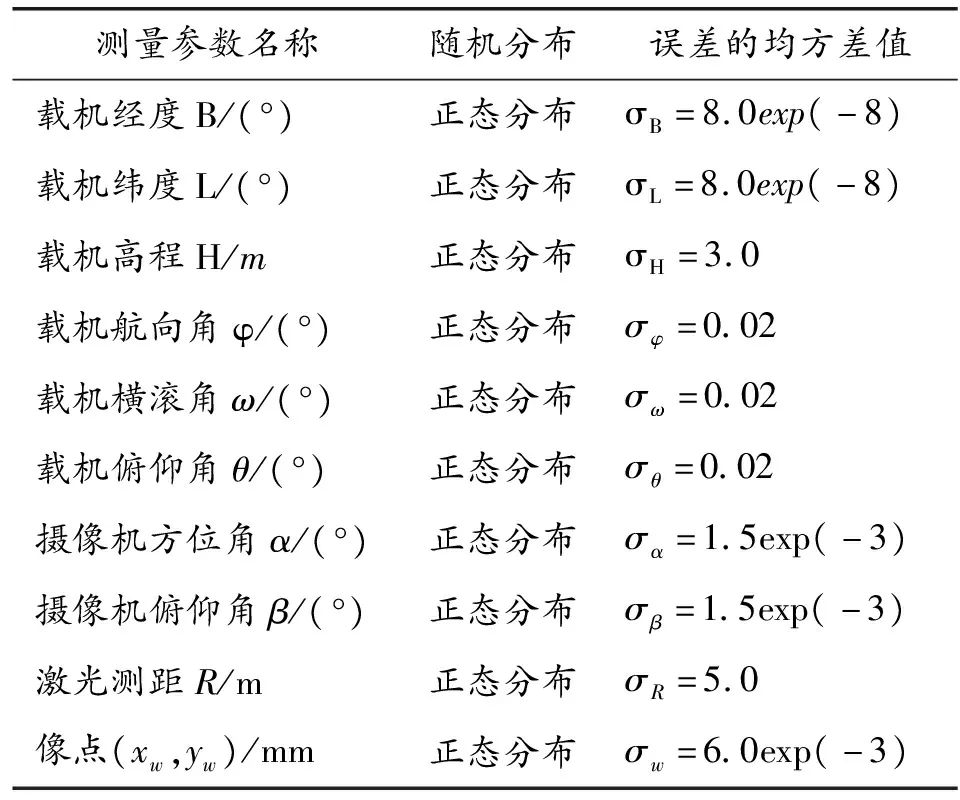
表1 測量參數隨機誤差分布的均方差值

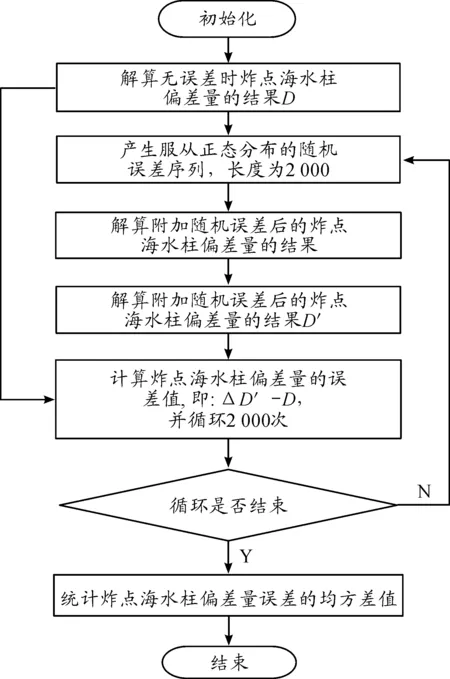
圖6 蒙特卡洛法仿真步驟框圖

3.2 仿真結果與分析

借助Matlab軟件按照圖6中的蒙特卡洛法仿真步驟編寫程序仿真得到2 000組炸點偏差量數據，并進行統計學分析，得到如圖8所示的仿真結果，其中，圖7(a)為多目標定位算法仿真結果，圖7(b)為差分組合定位算法仿真結果。對比圖7(a)與圖7(b)可以看出，兩種算法解算得到的2 000組炸點偏差量測量結果誤差均近似服從μ=0的正態分布；不同的是經過差分組合定位原理修正后，炸點偏差量誤差“體型”明顯變“瘦”，表明經過修正后的炸點偏差量誤差的均方差值有一定的減小。根據統計數值可知，經過差分組合修正后的炸點偏差測量精度提高4 m左右，因此，差分組合定位修正有效果。

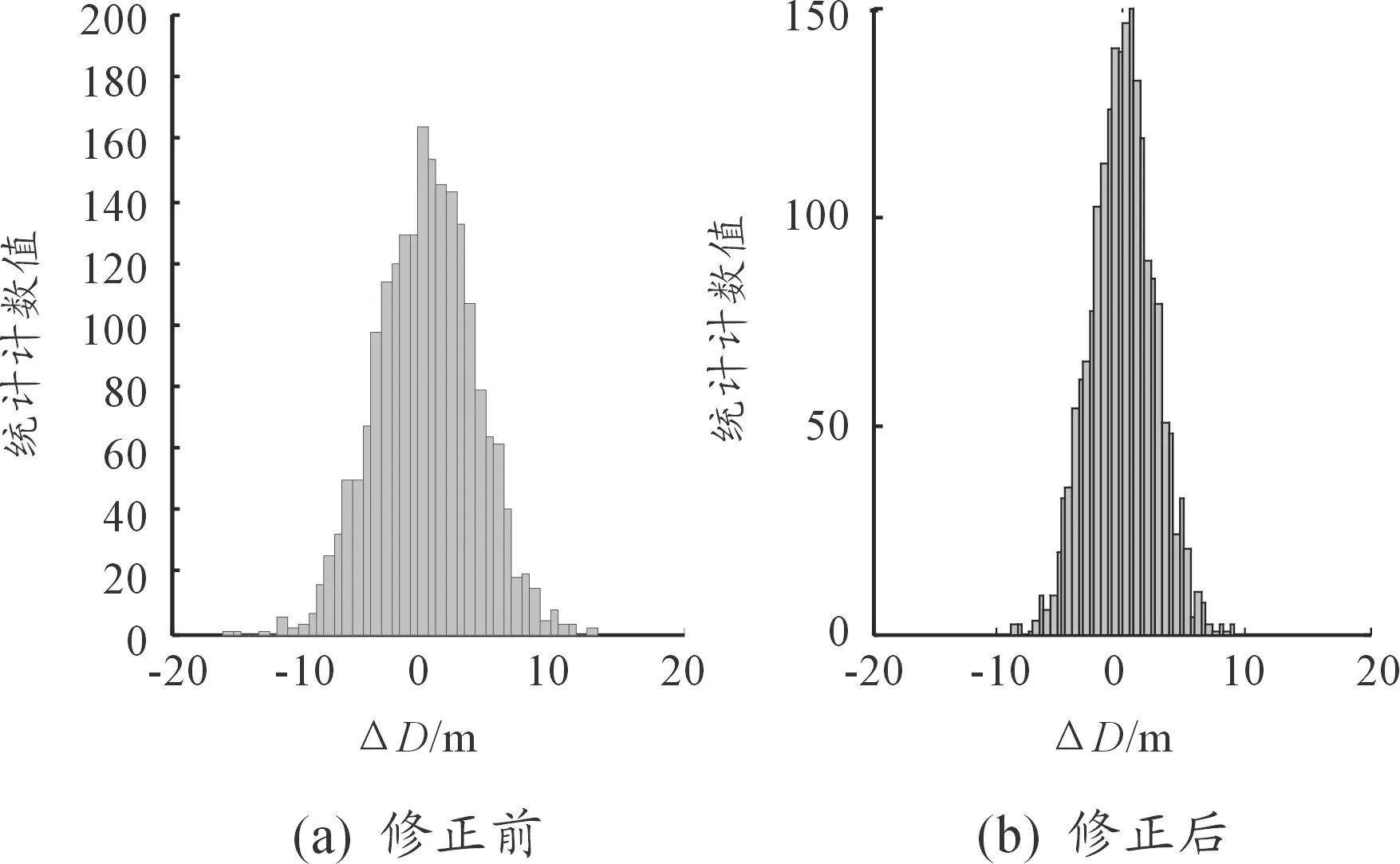
圖7 兩種算法解算的炸點偏差量誤差仿真結果

4 結論

基于差分組合定位原理推導出了艦炮對海射擊檢靶模型，可有效解決炸點海水柱測不到、測不準、檢靶效率低以及檢靶過程繁瑣等問題。通過差分組合修正后的炸點偏差量誤差的均方差值有一定減小，檢靶精度提高約4 m左右。

本研究未充分考慮無人機自身性能、靶場測試環境等局限對該檢靶方法的影響，艦載雷達設備開機時容易導致無人機失控“栽入”海中等。未來無人機技術不斷成熟，該方法對于解決艦炮檢靶難的問題具有積極作用。