圓周率知多少

王學志

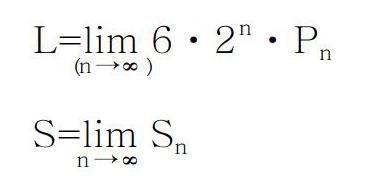
圓周率的計算

“圓，一中同長也”。意思是說：圓只有一個中心，圓周上每一點到中心的距離相等。早在我國先秦時期，《墨經》就已經記載了圓的這個定義。人們從認識圓到得出有關于圓的種種計算又經歷了相當長時間的探索。其中，圓周率就是橫在人們面前的一道壕溝。

傳統所認為的圓周率指圓的周長與直徑之比，最初產生于制作圓形工具的需要，并且是通過測量計算出來的，即圓底量法。目前，用符號π來表示圓周率。圓周率是一個常數，這一事實很早就為人們所知。在戰國時期的著作《墨子·小取》中就記載有“小圓之圓與大圓之圓同”的說法，可見，在墨子時代人們已經認識到圓的周徑之比是一個常數。

人們對圓周率的認識過程

在古代，巴比倫、印度、中國等在很長一段時間都是使用π=3這個數值。直到公元前2世紀，中國的《周髀算經》里仍然有周三徑一的記載，這個“圓徑一而周三”是我國最早關于圓周率的一個誤差較大的近似值，后人稱之為“古率”。直到東漢時才有數學家將π值改為約3.16。但真正使圓周率計算建立在科學基礎之上，首先應歸功于阿基米德。他專門寫了一篇論文《圓的度量》，用幾何方法證明了圓周率與圓直徑之比小于22/7，而大于233/71。這也是第一次在科學中創用上下界來確定近似值。這之后我國魏晉時期的劉徽第一次采用正確的方法計算出了π值。公元263年，他首創了用圓的內接正多邊形面積來逼近圓面積的方法，算得π值為3.14。我國稱這種方法為割圓術。直到1200年后，西方才找到了類似的方法。后人為紀念劉徽的貢獻，將3.14稱為徽率。

公元460年，南朝的祖沖之利用劉徽的割圓術，把π值推算到小數點后第7位，即3.1415926，這在當時世界尚屬首次。祖沖之還找到了兩個分數：22/7和355/113，用分數來代替π，極大地簡化了計算，這種思想比西方也早1000多年。

祖沖之的圓周率，保持了1000多年的世界紀錄。終于在1596年，這一紀錄被荷蘭數學家魯道夫打破。魯道夫先把π的值推算到小數點后第15位，最后又推算到第35位。為了紀念他這項成就，在他1610年去世后，人們在他的墓碑刻上了3.14159265358979323846264338327950288這個數。

近代計算機的發明，大大促進了科學的進步，到90年代初，人們已經可以將π的值精確到小數點后4.8億位。即便這樣，圓周率的計算仍然在繼續。我們已經清楚地知道，圓周率是一個“無限不循環小數”，而且還是一個超越數。但是科學家仍會像登山運動員那樣，奮力向上攀登，不斷探索下去。

劉徽的割圓術

劉徽到底是怎么計算出π值的呢？“割之彌細，所失彌少，割之又割，以至于不可割，則與圓合體，而無所失矣”，這句話是劉徽對于他的“割圓術”的描述。意思是說：圓內接正多邊形的邊數無限增加的時候，它的周長的極限是圓周長，它的面積的極限是圓面積。即“割圓術”實際上就是用圓內接正多邊形的面積去無限逼近圓面積并以此求取圓周率的方法，并且內接正多邊形的邊數越大，所求得的圓周率越精確。

劉徽從圓的內接正六邊形開始割圓，并且得到了一個正6·2n邊形面積序列。咱們不妨假設S是圓的面積，L是圓的周長，Sn是6·2n邊形面積，Pn是每邊長。顯然，n越大，S-Sn越小，即所謂的“割之彌細，所失彌少”。而“割之又割，以至于不可割，則與圓合體，而無所失矣。”用現代數學公式表示就是：

L=lim 6·2n·Pn

S=lim Sn

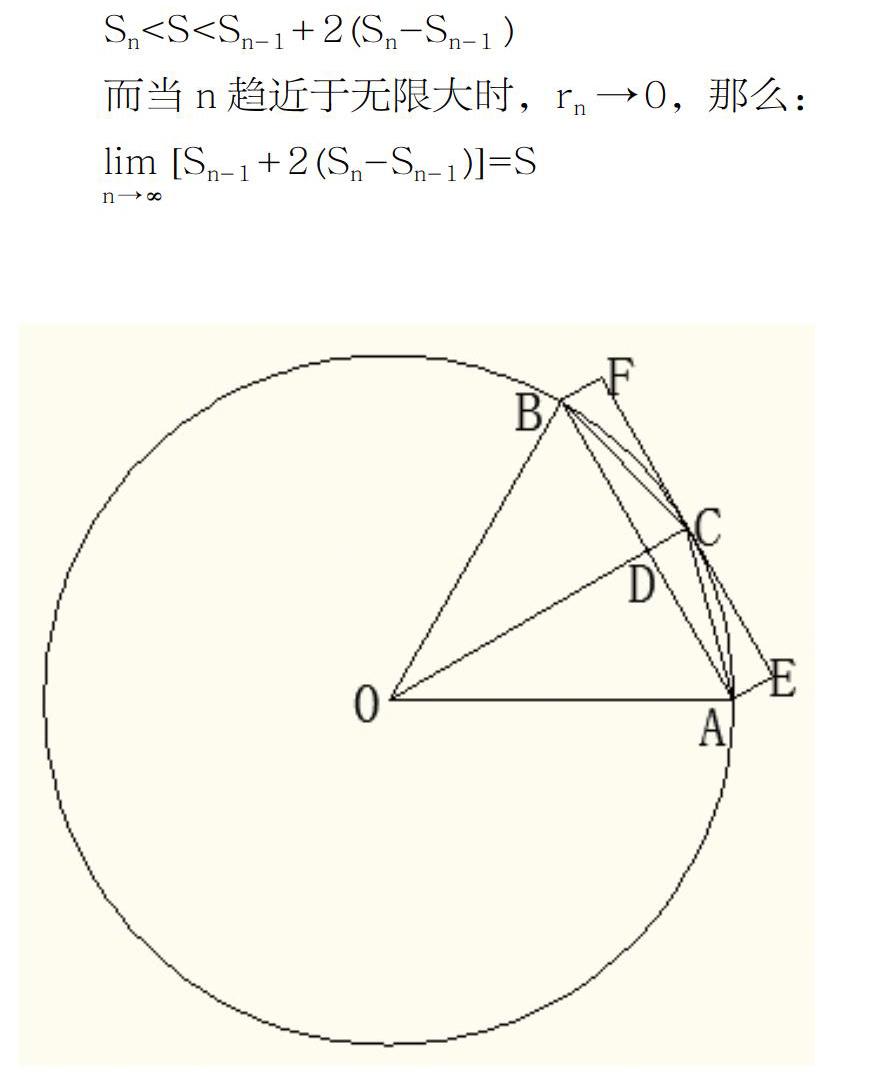
所謂“余徑”，就是指半徑減垂徑所剩的長度。在下圖中，6·2n-1邊形的余徑就是指線段CD。那么，余徑乘以邊長就是6·2n-1邊形余徑長方形ABFE的面積。△ACB稱為6·2n-1邊形余徑三角形，其面積為其余徑長方形面積之半。從圖中可以看出Sn-Sn-1的值等于6·2n-1個余徑三角形的面積之和，圓的面積大于6·2n邊形面積Sn，小于6·2n-1邊形面積Sn-1加上6·2n-1個余徑長方形的面積。即：

Sn

而當n趨近于無限大時，rn→0，那么：

lim [Sn-1+2（Sn-Sn-1）]=S

假設圓的半徑為1，劉徽利用這種方法算出了圓內接正192邊形的面積3.141024與圓內接正96邊形的面積3.139344，得出了圓面積范圍：3.141024