區間規劃下的高殘值易逝品供應鏈網絡設計

陳 勇，楊雅斌

1.佛山職業技術學院 工商管理學院，廣東 佛山528137

2.廣州工商學院 物流系，廣州510850

1 引言

隨著信息技術的發展和普及，企業為了爭奪市場份額往往會在新產品上市不久后就投入巨資研發下一代產品，這樣就極大地縮短了產品的生命周期，尤其是電子類消費品和高科技產品。這些產品市場價值消逝極快但核心部件仍然具有較高的使用價值，稱之為高殘值易逝品。因此，為了及時充分挖掘這些產品的剩余價值，企業需要加快產品的回收并進行高效處理。許多企業為了盡快將這類產品在生命周期內銷售出去，往往設法開拓電商銷售渠道。同時，對高殘值易逝品回收處理再利用可以為企業和社會帶來顯著的品牌和環保效應。

進入21 世紀，隨著循環經濟理念的發展，大量學者針對再制造閉環供應鏈進行研究，主要研究工作集中在四方面：閉環供應鏈的定價[1-3]、閉環供應鏈的回收渠道[4-6]、傳統閉環供應鏈網絡設計[7-9]，以及考慮碳排放的閉環供應鏈環保問題[10-12]。姚衛新考慮正、逆向物流以及電子商務對供應鏈的影響，構建一個包含正、反向的閉環供應鏈物流網絡成本模型[13]。陳娟認為再制造閉環供應鏈的實施會產生潛在的經濟收益，構建了一個單、雙渠道下的正向和反向供應鏈模型，仿真結果表明產品的銷售率和回收速度對經濟收益有影響[14]。張桂濤等提出一個由供應商、制造商、零售商組成的三級網絡模型；其中，制造商的產品通過線上線下渠道銷售給消費者，產品被使用后產生的廢舊品經由回收中心處理送往制造商重新再制造的閉環供應鏈網絡均衡模型[15]。盧榮花基于產品生命周期理論研究只包含制造商和零售商兩個決策主體的閉環供應鏈，建立了兩周期的分散決策模型，結果表明：二者應根據不同的成本節約額制定不同的批發價、零售價和生產量[16]。于春海等設計只包含制造商和零售商兩個決策主體的雙渠道供應鏈結構，將銷售期分為兩個銷售階段，運用博弈論建立決策模型，并引入改進的收益共享契約有效解決渠道沖突問題[17]。李曉婧等將碳交易和碳排放納入碳管理中，考慮原料的使用率和政府約束的再制造率，建立一個包含供應商、制造商、銷售商、消費者和回收中心的雙渠道閉環供應鏈網絡均衡模型[18]。

以上文獻的研究對象大多數集中在普通制造品上，很少研究高殘值易逝性產品。許多學者在設計閉環供應鏈網絡時考慮的因素不全面，尤其是沒有考慮企業所掌握的已有信息，而片面地給產品需求量做一個單一假設。現實中，制造企業開發的新產品往往可分為大眾消費者喜愛的產品和經常更新換代的產品。前者由于每年的銷量穩定，新產品只是對舊產品的局部功能做簡單改良而不完全顛覆，因而其回收量數據可以用一個區間數估計；而后者是為了滿足特定的人群，其產品更頻率高，因而這部分需求很難通過一個區間數來描述，此時，回收量采用一個隨機參數估計比較有意義。因此，為了快速獲取高殘值易逝性產品的價值，在設計此類產品的閉環供應鏈網絡時必須綜合考慮高殘值易逝性產品的回收點，回收成本與回收時間的關系，新、舊產品定價，以及回收量的不確定性。

在供應鏈網絡規劃中，一般都采取隨機、模糊和區間等方式來描述事件的不確定性，并據此做出有利決策；然而采用前兩種方法對不確定性問題進行優化時，需要知道參變量的相應函數關系，而實際上要獲取這些分布函數并不容易[19]。但用區間數來表示參數的波動范圍是很容易做到的，尤其在參變量分布未知的情況下，采用區間規劃簡單實用，產生的區間解可為決策者縮短決策范圍。本文基于高殘值易逝品的生命周期理論，考慮回收時間的價值性，以網絡收益最大化為目標，建立了區間機會約束環境下的多產品、多周期、多渠道的閉環供應鏈網絡模型。

2 模型建立

2.1 問題描述及假設

本文描繪的再制造閉環供應鏈網絡結構由制造/再制造商、中間商、消費區、回收中心組成，如圖1 所示。當新一代產品被研發出來后，制造/再制造商為了快速搶占市場，將新產品大規模地布局到中間商，中間商則快速地銷往傳統消費區（一級消費區）。為了降低企業的制造成本并承擔起社會責任，制造企業將對這些高殘值易逝性產品進行定期回收，回收源主要來自傳統消費區使用過的舊品和中間商處的滯銷品。對于沒有質量問題的產品則可以在電商市場和二級市場進行二次銷售，而對于沒有直接銷售價值但其核心部件仍然完好無損的產品則經過回收中心處理后直接運往制造/再制造商處，進行下一代產品的再制造處理。

圖1 基于電商環境下的高殘值易逝品閉環供應鏈網絡結構

在圖1 構造的網絡中包含諸多不確定性因子，主要是區間參變量和隨機參變量這兩類。為了有效地處理這兩類參變量，本文擬采用區間規劃和隨機規劃進行確定性轉換。企業根據以往的銷售歷史數據可得到二手市場的產品需求分布函數，充分利用了其信息價值；同時該需求函數不能確保百分之百滿足所有的約束條件，即它存在違背約束條件的風險，因而這部分需求采用機會約束方法描述較合理；對于產品的回收質量、回收成本、電商市場需求以及各個設施的處理能力等參數很難獲取其分布信息，可以用區間表示這些不確定參數。

根據問題描述，在建立模型之前，給出以下假設：

假設新部件和再制造部件給消費者帶來的產品效用都是一致的，不考慮產成品和零部件丟棄掩埋的處理成本，并且中間商滯留的合格產品不存在貨損；產品生命周期包含成長期、成熟期和衰退期三個階段，制造商對產品進行回收，產品回收時間發生在各階段的末期。制造商在每一階段的回收點如圖2所示。

圖2 產品在生命周期中的回收點

在成長期和成熟期末，對回收來的產品進行質量診斷和分類，對于不影響二次銷售的產品則輸出到電商消費區域與新產品同時銷售，對于一些功能良好，只需要稍加維修、清潔就能將再利用的產品銷往到二手市場；對于功能完全受損的產品則運回到制造/再制造商進行下一代產品的制造；在衰退期末，產品在三個階段內結束銷售后，便向一級消費區和中間商回收廢舊品和滯銷品，所有產品不再作質量診斷劃分全部被運往制造/再制造商處進行再制造，而不再重新銷往消費區域，以避免與新一代產品產生沖突。

當銷往電商和二手市場的產品存在缺貨時，需要承擔相應的違約成本。其他假設如下：

假設1回收率和產品回收價格成線性關系[20]，則有方程：

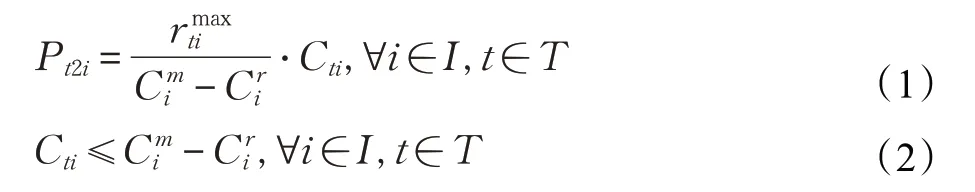
假設2產品的回收時間長短與處理成本大小成反比關系[14]，可采用成本-努力函數來表示產品的回收時間和處理成本的關系，其中，b為努力成本系數，ρ為努力強度。則有方程：

其中，CDti和CCti分別表示t 階段從中間商處和一級消費區回收一單位產品i 所需要的收集處理費，包括產品的儲存費和配送費；c 與cc分別表示從中間商和一級消費區回收的單位產品進行質量等級劃分所需的固定處理成本，hti與mti分別表示t 階段產品i 從中間商和一級消費區回收所需的時間；根據假設，有bc≥b,cc≥c。

假設3產品的市場淘汰率是恒定的，產品的生命長度與滯銷率的關系[21]：

其中，Lti表示t 階段產品i的生命長度，f( Lti)i表示Lti的函數。由此可知，產品的滯銷率跟生命周期長度有關，如果產品的生命周期趨于∞，該產品不存在滯銷。

假設4產品的價值隨著時間的推移在不斷地下降，具體表現在其價格的下跌[22]。假設回收的產品在電商消費區、二級消費區以及回收用于下一代零部件再制造的時間折現因子分別是ηn、ηm、ηng,ω(0 ＜ω ＜1)為價格系數，則t 時刻的銷售價格可表示為：

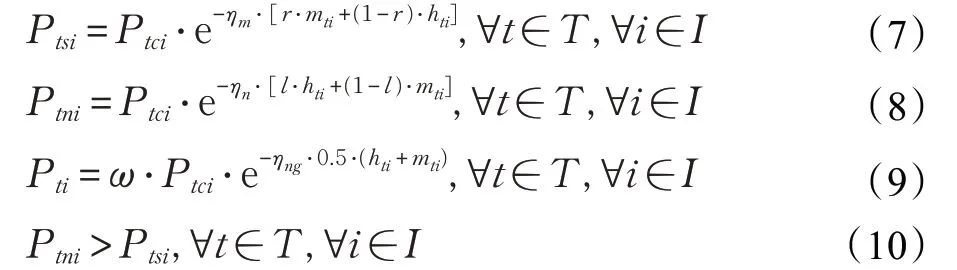
其中，Ptci表示t 階段新產品i 的銷售價格，Ptsi、Ptni、Pti分別表示t 階段產品i在二級消費市場、電商消費區域以及廢舊品、滯銷品所回收的零部件用于下一代新產品再制造的銷售價格，其價格與新產品的售價、中間商回收時間、一級消費區回收時間有關；為避免渠道競爭，假設回收的產品銷售到二手市場的價格要低于電商市場的價格，同理可得電商市場的價格要低于新產品的售價。

假設5產品從中間商和一級消費區域的回收時間不能超過該類產品下一階段的時間長度。隨著產品更新換代速度加快，衰退期末產品的回收時間必然要小于下一代新產品的成長期，而下一代新產品相對于上一代產品的各階段長度將明顯縮小。因此，衰退期末的產品回收時間要小于本代產品的成長期。

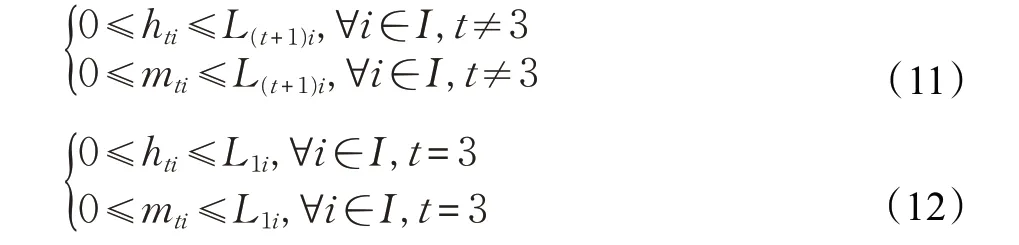
2.2 模型參數與決策變量

2.2.1 下標

I：制造/再制造產品類別的集合，i ∈I;J：中間商的集合，j ∈J;K：一級消費區域集合，k ∈K;V：回收處理中心的集合，v ∈V;T：生命周期階段的集合，t ∈T。

2.2.2 決策變量

2.2.3 參數

（1）能力約束

（2）比率量

（3）費用

（4）收益

2.3 目標函數

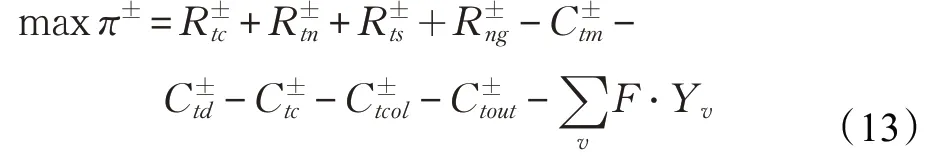
（1）各渠道的銷售收入，包括正向供應鏈在傳統市場的銷售收入、逆向供應鏈在二級/電商市場的再銷售收入以及零部件用于下一代產品再制造的銷售收入。

（2）各供應鏈成員的成本，主要包括制造/再制造商、中間商、一級消費區域、回收中心、再銷售過程等發生的費用。

約束條件：

（1）流量守恒：分別表示制造/再制造商、回收中心、中間商、一級消費區的流量平衡。

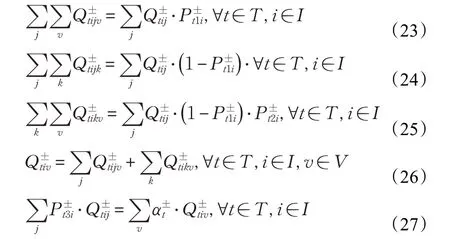
（2）能力約束：分別表示制造/再制造商、中間商、回收中心的最大服務能力限制。

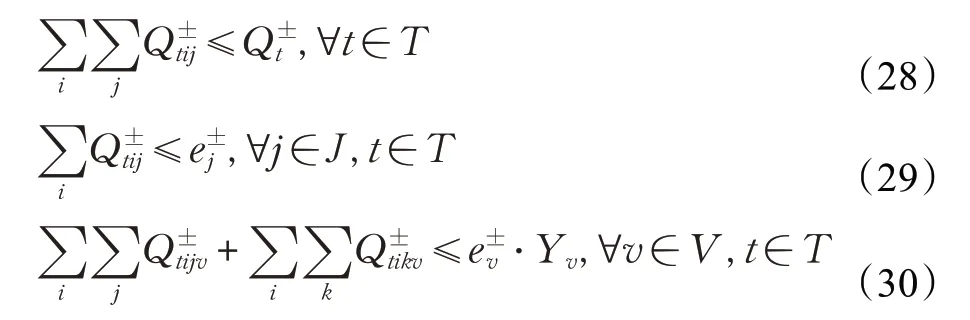
（3）回收中心選址約束：回收中心選址屬于二元事件，用0-1規劃表示，Z 表示備選回收中心的數量。

（4）再銷售需求約束：二級消費區域和電商消費區域對產品的需求量約束。

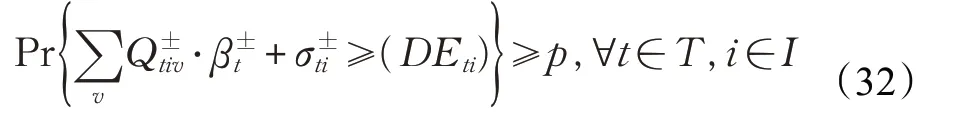
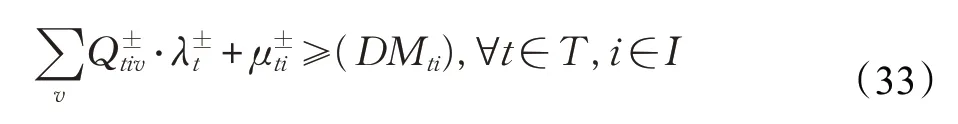
（5）其他約束：對于網絡模型而言，各參數及變量應為非負的。

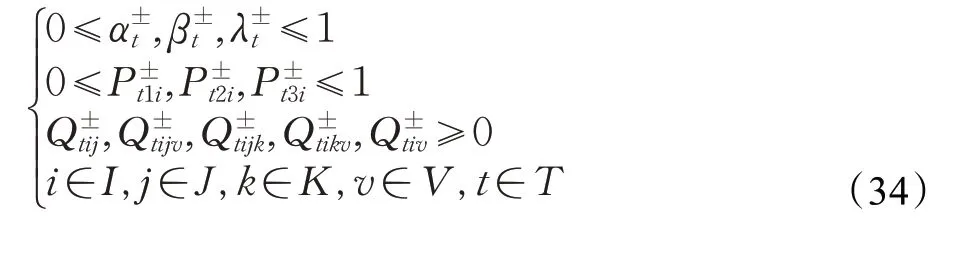
2.4 確定性轉化

在數學規劃中，根據實際問題所建立的數學模型，如果只考慮部分變量取為整數值，則稱為混合整數規劃。在區間規劃的基礎上融合混合整數規劃方法形成區間混合整數規劃（Interval Mathematical Linear Programming，IMLP），用于解決模型中含有整數決策變量的區間不確定性的數學規劃問題。區間混合整數規劃的一般形式如下：

對于區間整數規劃的轉化，可參照Huang[23]利用特定的相互作用的兩階段法去求解區間模型，即如果目標函數是要求最大化的話，則先模擬對應上限的子模型(f+)并進行求解，然后根據上限模型求得的解，模擬求解下限子模型(f-)，最后對兩個子模型所求的解進行合并得到一個區間值。上限子模型的形式如下：

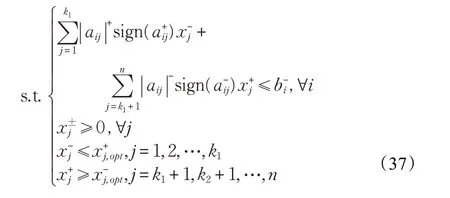
機會約束規劃對每個約束i都有一個確定的概率水平pi，同時需要保證每個約束條件至少在pi的概率水平上成立。一般地，機會約束規劃的不確定性能夠分別表現在模型的目標函數和約束條件中。機會約束規劃轉化如下：

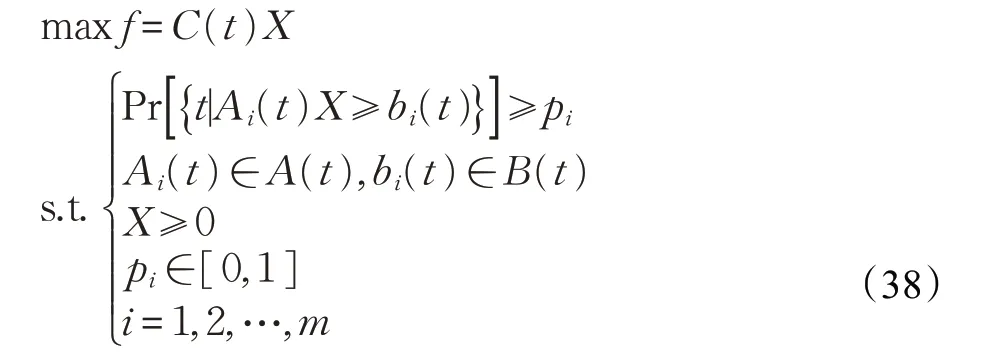
若A是確定的，B是隨機變量，B的累積分布函數為F(bi),bi(t)pi=F-1(pi)，則根據隨機變量累積分布函數的定義可知：

若 AiX=bi(t)pi, 則 Pr[ {t |AiX ≥bi(t)} ]=；piAiX ≥bi(t)pPi,r[ {t |AiX ≥bi(t)} ]≥p，i由 此 可 知AiX ≥bi(t)pi等價于Pr[{t|AiX ≥ bi( t)} ]≥p。i初始問題等價轉化為：

通過以上確定性方法轉化，利用Lingo 編程求解可以獲得目標函數π±、滯銷率、回收率、再制造率、電商售價、二手市場售價、零部件的售價以及從中間商、一級消費區域回收產品的時間等的最優解。

3 算例描述與求解

3.1 算例描述

已知某高殘值易逝性產品的生命周期包括3 個階段，其閉環供應鏈網絡結構由1個制造/再制造商、3個中間商、4個一級消費區、1個二級消費區、1個電商消費區和3個備選回收中心構成。產品1、2在一級消費市場的售價分別為2 500 元、3 500 元；制造商到中間商的單位產品運費為0.003元/km；中間商到所有一級消費區和回收中心的運費都為0.005 元/（km·件）；一級消費區到所有回收中心的運費為0.004 元/（km·件）；回收中心到制造/再制造商和二級消費區的運費為0.003 元/（km·件）和0.004 元/（km·件）；電商銷售的運輸成本為15 元/件。3個周期階段下產品1的回收率為0.7、0.6、0.5，產品2的回收率為0.8、0.7、0.6。備選回收中心1、2、3的固定投資成 本 依 次 為550 000 元、520 000 元 和500 000 元；

cc=50,c=25,b=0.6,bc=0.8,ηn=0.4,ηng=0.5,ω=0.15,r=0.6,l=0.65,ηm=0.42。周期長度和需求信息如下：

（1）周期長度

表1 產品在各個生命周期階段的回收成本和周期長度

（2）需求信息

假設至少滿足二級消費區域不缺貨的概率p 為0.95，而對于二級消費區域下的產品需求可以通過已有數據來模擬生成需求分布函數，假設該消費區的需求量服從正態分布函數。成熟期，二級消費區對產品1、2 的需求分布函數分別為N(220,302)，N(150,282)；電商市場在成長期和成熟期對產品1 的需求為[300，350]、[200，250]，對產品2的需求為[250，300]、[150，200]。

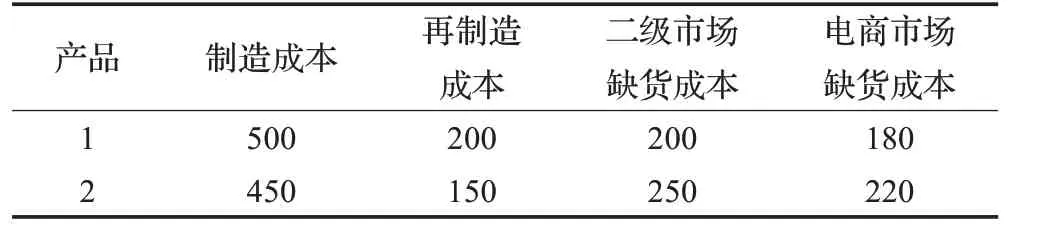
表2 產品的制造/再制造成本及市場的缺貨成本（元/件）

表3 產品i在中間商j和備選回收中心v的庫存費用 元

（3）其他參數

產品的各項成本費用、可再利用率、設施間的距離和服務能力約束如表1至表7所示。

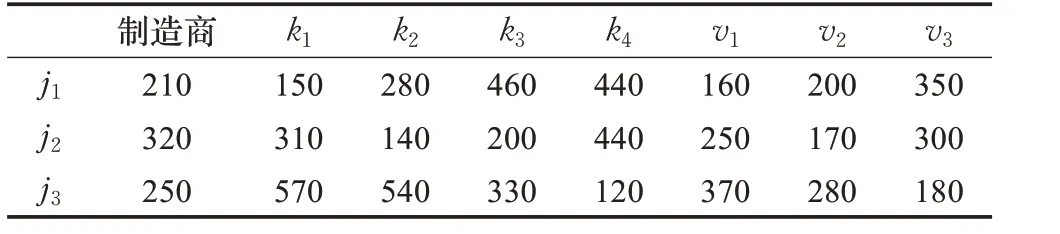
表4 中間商j到制造/再制造商、一級消費區域k以及備選回收中心v的距離km

表5 制造/再制造商、二級消費區域到備選回收中心v的運距km

表6 經回收中心加工后，流入各個市場的產品分布比例

表7 制造/再制造商、中間商和回收中心的服務能力約束

3.2 算例求解

根據以上數據，取p=0.95，在CPU Intel?CoreTMi5-7500為3.40 Hz、內存為8.00 GB運行環境下，采取總耗時2 s，經過884步迭代，得到最大利潤區間為[21 086 910，25 716 790]，Y1=[1,0],Y2=1,Y3=[0,1]，模型的其他解見表8。

企業最大利潤的平均值為23 401 850 元，偏差為2 314 940元，偏差率為9.9%。在網絡優化的過程中，回收中心的選址是重點考慮的內容，通過分析可知，在2號備選地必須建立回收中心，而1 號備選地在求最小目標值時需要進行考慮，在求最大目標值時，應考慮3 號備選地；企業應該結合自己的戰略定位考慮是否對1、3號備選地建設回收中心：比如，采取收縮性戰略的企業急需回籠資金，減少固定資產投資，因而可以選擇固定投資成本較小的3 號回收中心；若處于擴張型戰略的企業，追求市場占有率是其首要目的，因此，應當考慮在回收處理能力較大的1號備選地設立回收中心。

根據產品所處不同生命周期，其表現出的網絡不確定性也不一致，由表8 結果可知，通過比較各參數的總體偏差率發現，衰退期的產品最穩定。通過比較又可發現產品1各項參數的波動較產品2大。產品的價格與回收時間密切相關，回收時間不確定性越大，造成的產品價格偏差較大。如產品1 在成熟期的中間商回收時間為[0.097，1.48]，其銷往再制造廠的價格為[182，345]，偏差率達到30.93%。產品1 在成長期和成熟期存在缺貨風險，在成熟期，產品1 銷往二級消費區缺貨量為57，銷往電商消費區缺貨量為[67，83]；在成長期，產品1 銷往電商消費區的缺貨量為[100，117]。

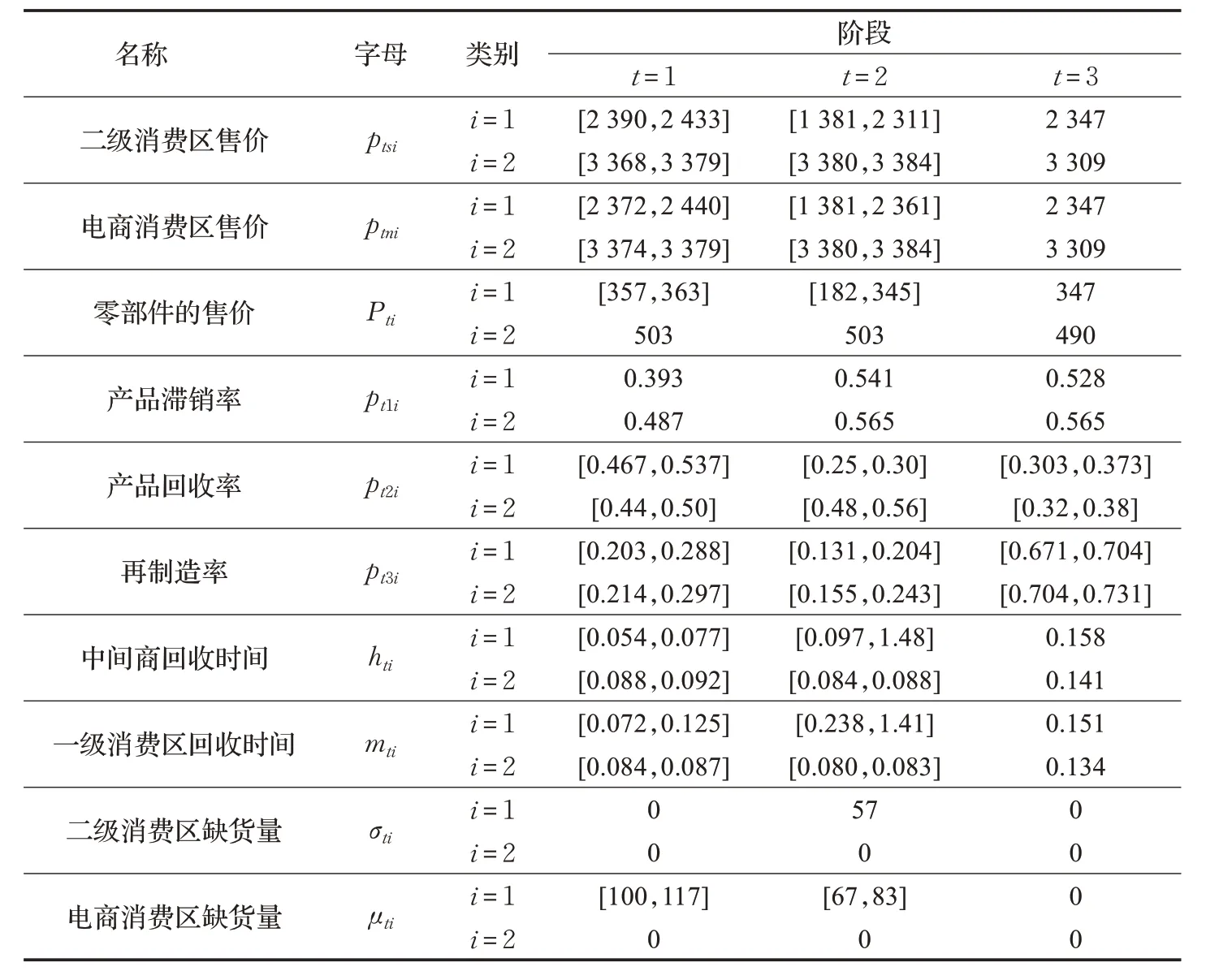
表8 區間機會約束方法下不同階段各決策變量最優解

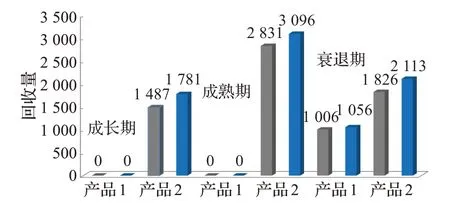
圖3 產品1和產品2在回收中心的流量

三個階段下，兩種產品經過回收中心的流量如圖3所示，灰色立體柱代表最低流量值，藍色立體柱代表最高流量值。由圖可知，由于產品1 在二級市場和電商市場均存在缺貨情況，所以產品1 在這兩個階段沒有回收量，產品1 在衰退期的回收量為[1 006，1 056]。由于產品2的制造和再制造成本比產品1低，加之其殘值較高，導致產品2 在二級市場和電商市場的銷量比產品1 高，所以在每一階段中，產品2的回收量都會高于產品1。

綜上，企業應該重點關注產品1 的回收時間和缺貨量，根據產品1 在市場的銷售情況和庫存水平，應該縮短產品1 的回收時間，適當提高二級市場和電商市場的價格，同時加大產品2 的投入生產，發揮回收中心的作用。受篇幅限制，其余各個節點的流量不再贅述。

為了檢驗模型的穩定性，將置信水平p 分別取0.95，0.85，0.75，0.65，0.55 時，所得的最優選址決策方案和目標函數值如表9 所示。由結果表明，網絡選址決策不受p值影響，證明該模型具有穩健性。當至少滿足二手市場不缺貨的概率越大時，企業所需承擔的風險就越小；即隨著p值增大，企業獲得的利潤就越大，但增幅甚微。因此，企業在缺貨的情況下所承擔的缺貨成本比較小，可以考慮提高產品的價格，從而獲取更多的利潤。

表9 置信概率p對目標值和決策點的影響

4 結束語

本文針對高殘值易逝性產品的特性，基于產品生命周期理論建立了雙渠道環境下的再制造閉環供應鏈網絡模型。該模型主要創新點是分析產品從各個渠道的回收時間和產品所處的生命周期長度之間的關系，最終目的是減少產品從其他渠道的回收時間，極大地利用產品的剩余價值。對于模型中的不確定性參數，采取了區間機會約束混合整數規劃方法進行不確定性轉化，數值仿真所得的結果可以為企業在設施選址、產品定價、產品回收時間、產品銷量等提供決策依據。最后通過分析不同置信水平條件下的目標值，驗證了該模型的穩健性。

本文將中間商和回收中心分開來考慮，下一步研究則可以將二者合并成一個主體，在環保理念和制造商返利的誘導下，中間商將主動承擔產品回收，從而構建一個新的閉環供應鏈網絡。區間規劃理論應用于閉環供應鏈網絡求解的案例比較多，該方法雖然簡單可行，但是所得的區間解若是太大，則對決策者沒有參考價值，因此下一步研究需要給區間設定一個度，即決策者在可承受的區間范圍內所做的決策。