基于K-Means和CNN的用戶短期電力負荷預測①

呂志星,張 虓,王沈征,王 一,程思瑾,秦承龍

(國網山東省電力公司 泰安供電公司,泰安 271000)

1 引言

智能電網的發展推動了用戶側智能電表的普及,同時各種監控系統的大規模部署使得電網公司能夠獲得多尺度、全方位的用戶用電信息[1],這些大量、高分辨率的用戶負荷數據不但可以用于刻畫用戶用電習慣,還可以對用戶的用電負荷進行預測,因此,挖掘用戶負荷數據對于電網系統的調度優化、精細化經營管理以及服務于市場用戶等方面具有重要價值[2].

長期以來,負荷預測是電力系統的研究熱點之一.按照時間期限分類,電力負荷預測可以劃分為長期負荷預測(10 年及以上)、中期負荷預測(5 年左右)和短期負荷預測.其中,長期負荷預測主要用于電力系統未來規劃,短期負荷預測主要是為了合理安排發電機組的啟停、減少旋轉備用容量,從而降低發電成本、保障電網的安全穩定性.根據電力負荷數據時序性和非線性的特點,短期負荷預測模型一般可以分為兩類,一類是時間序列方法,通常是將電力負荷看成一種時間序列的集合,根據電力負荷的歷史數據、相關影響因素構建預測模型,從而實現預測未來負荷值.常用的方法包括:傅里葉展開法[3],指數平滑模型[4],自回歸積分滑動平均模型[5].這些傳統的時間序列方法對歷史數據隨時間的平穩性要求比較高,在一定程度上過于強調對歷史數據的擬合,導致預測精度不高.另一類是以機器學習為代表的人工智能方法,主要包括:統計機器學習方法中的隨機森林算法(Random Forest,RF),支持向量機,以及深度學習方法中的長短期記憶網絡(Long Short Term Memory,LSTM)等.鄒云峰等[6]將數據類進行K-means 聚類后分別進行線性回歸,在線損率預測上取得較好結果,但由于其采用線性回歸,對非線性數據建模能力有限.黃晗等[7]提出了基于隨機森林的方法,針對歷史負荷數據和天氣信息對某地區進行預測.文獻[8]將小波變化與極限學習機組合,提出了一種集成學習預測模型.以上方法相較于傳統的預測方法有了很大的提升,但難以兼顧到時序數據時間相關性.文獻[9,10]利用了LSTM 的時間序列性,可以更好地預測非穩定狀態的負荷數據.雖然這些方法可以在系統級負荷預測上取得很好的效果,但由于單個用戶用電的波動性和隨機性較大,系統級負荷預測方法在單個用戶的負荷預測上的預測性能較差,無法滿足電網精益化管理的需求.

當前短期負荷預測多以電網系統級負荷為研究對象,而對于用戶級對象的研究工作較少.文獻[11]研究了不同內核的支持向量回歸(Support Vactor Regerssion,SVR)模型對單個家庭用電負荷的預測效果.文獻[12]針對呈指數級增長的電力用戶數據提出一種改進的并行化的基于隨機森林的負荷預測方法.文獻[13]考慮到了用戶用電行為的變化,提出了擴展卡爾曼濾波及核函數極限學習機相結合的方法對用戶側短期負荷進行預測.文獻[14]提出了一種基于決策樹和小波去噪相結合的預測方法,對不同用電模式的用戶進行個性化負荷預測.這些模型考慮了用戶用電負荷影響因素,對不同用戶的用電特性進行分析,但忽略了時間序列相關性對單個用戶負荷預測的影響.

從相關工作來看,對于用戶電力負荷預測而言,需解決兩方面問題:一是如何有效提取與預測目標相關的抽象特征,以便預測模型學習其中規律;二是不同用戶負荷特點差異較大,單一預測模型不能對特征差別較大的用戶進行負荷預測,建立組合預測模型以提升預測精度是很有必要的.因此,本文從用戶負荷數據特性出發,利用K-means 聚類得到不同用戶類別,針對每類用戶的負荷數據時間相關性,搭建不同的負荷預測模型.為了能夠提取與負荷相關的抽象特征,本文利用不同時間序列信息構建不同張量作為卷積神經網絡的輸入,構建出深層卷積網絡來預測單個用戶的負荷.最后,本文結合某地23 個用戶一年的真實用電負荷數據對本文提出的方法進行驗證.

2 基于K-means 聚類算法的用戶分類

圖1 為隨機選擇的5 個用戶的某周負荷曲線圖,不同顏色的曲線表示不同用戶的周負荷變化情況.其中,橫軸表示時刻點,每15 分鐘采樣一次負荷數據,縱軸表示負荷數據.通過觀察曲線發現,對于單個用戶而言,由于生產和經營一般具有較強的周期性和規律性,其日負荷數據也具有規律性,具體可以表現為以下2 個方面:如無重大突發情況,其短時間內負荷曲線波動較小(相鄰時刻相關);不同日的相同時刻的負荷波動差異不大(日相關).為此,首先我們利用K-means 聚類算法來研究用戶用電行為模式.

K-means 算法是一種無監督學習方法,算法通過設定好的中心點對靠近它們的點進行歸類,通過迭代的方式,逐次更新各聚類中心的值,直到得到最好的聚類結果.對處理大數據集而言,K-means 聚類算法保持了較高的可伸縮性和高效性.算法描述如下:

(1)選擇合適的k值作為聚類的初始中心點.

(2)計算其他的點到這k個中心點的距離,離哪個中心點的距離最小就被劃分到哪個類.距離的具體計算公式如下:

(3)通過求平均值的方法更新該類的中心.

(4)按步驟(2)、(3)迭代更新后,直至各類中心點的值均不再變化,迭代結束.

圖1 某5 個用戶一周的負荷曲線圖

本文采用K-means 算法對真實數據集中的23 個用戶的歷史數據進行聚類分析,然后按照其時間序列的不同的相關性,將不同類別的用戶負荷序列轉換為張量后輸入至不同的卷積神經網絡進行抽象特征提取.聚類得到的結果如表1 所示.其中,A 類表示日相關性和相鄰時刻相關性均較為明顯的用戶,B 類表示僅相鄰時刻相關性較強的用戶.

表1 用戶聚類結果

3 基于CNN 特征提取的負荷預測模型

3.1 卷積神經網絡

在深度學習的諸多算法中,卷積神經網絡(Convolutional Neural Networks,CNN)因其特殊的網絡結構,在計算機視覺領域應用廣泛.然而,在電力負荷預測方面的應用較少.CNN 的典型網絡結構由輸入層、卷積層、池化層、全連接層和輸出層組成[15].其中,卷積層是CNN 的核心,包括卷積核、卷積層參數和激勵函數3 個重要部分.卷積層內部包含多個卷積核,組成卷積核的每個元素都對應一個權重系數和一個偏差量,類似于前饋神經網絡的一個神經元.CNN 的優勢在于能夠通過較少的權重參數訓練提取得到特征[16].

本文采用CNN 網絡來提取用戶歷史負荷的特征.對于A 類用戶,CNN 模型用相鄰的前16 個負荷數據點和待預測點前16 天的相同時刻的數據點分別構造成 4×4的矩陣形式,將這兩個矩陣組成的張量作為CNN 模型的輸入,如圖2 所示.

圖2 A 類用戶卷積神經網絡結構圖

對于B 類用戶,模型僅以相鄰的前16 個負荷數據點構建為 4 ×4×1的網絡輸入,如圖3 所示.CNN 模型有兩個卷積層,卷積核分別為2 ×2×32和 2 ×2×64.

圖3 B 類用戶卷積神經網絡結構圖

考慮到輸入數據的維度不高,因此本文在卷積層后直接接了兩個全連接層,而未使用池化層進行下采樣,保證了數據的完整性.模型使用ReLU 作為激活函數,選擇均方誤差(Mean Square Error,MSE)作為損失函數.

3.2 算法流程

將歷史負荷數據經過數據預處理得到用戶用電負荷曲線,通過K-means 聚類將用戶分為日相關性強和相鄰時刻相關性強的兩類用戶.針對不同用戶負荷特性,構建不同張量輸入的CNN 模型,具體處理流程如圖4 所示.

圖4 基于K-means 和CNN 的用戶短期電力負荷預測流程

4 實驗及結果分析

4.1 數據說明與數據預處理

本文所用數據集為某市23 個用戶2015 年全年的負荷數據,每15 分鐘采集一個樣本點,每天可獲得96 個負荷點數據.通過觀察數據,發現原始采集數據存在缺失、數據為負或遠大于該用戶其他時刻點的負荷數據等失真情況.因此在用于模型訓練和測試前,本文首先對采集到的負荷數據進行異常處理.對于缺失或失真的數據,本文利用該數據的前15 個相鄰數據點的平均值對其進行填充或修正,得到完整的負荷數據序列.同時,將所有的負荷數據通過歸一化映射到[0,1]之間,公式如下:

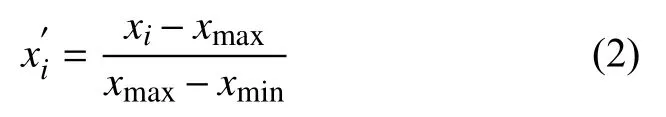
其中,xi為原始負荷數據,為歸一化后的負荷數據,xmax為數據集樣本中的最大負荷,xmin為數據集樣本中的最小負荷.

4.2 評價指標

為了有效評價模型的準確度以及與其他方法進行對比,本文選取平均絕對誤差(Mean Absolute Percentage Error,MAPE)作為評價指標,計算公式如下:

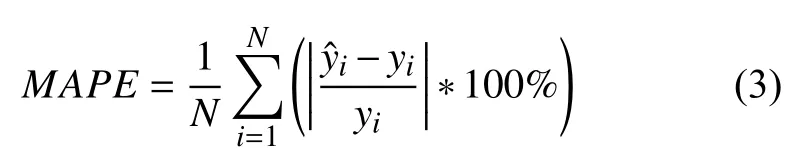
其中,n表示預測點的個數,yi表示第i個預測點的負荷真實值,表示第i個預測點的負荷預測值,即MAPE值越小,預測準確率越高.

4.3 預測結果分析

采用本文提出的CNN 算法對經過K-means 算法分類的電力用戶進行負荷預測,訓練集與測試集劃分比例為8:2.訓練集采用的是2015 年1 月1 日至2015 年10 月15 日的數據,共有28 128 條記錄;測試集采用的是2015 年10 月15 日至2015 年12 月31 日的數據,共有7007 條記錄.

(1)將本文模型與隨機森林和支持向量回歸機進行比較,結果見表2.

表2 不同電力負荷預測方法MAPE 比較(%)

本文模型對絕大多數用戶的預測效果都優于現有算法,平均MAPE為30.91%,相對于現有最好的RF 方法MAPE降低了20%,說明本文模型可有效提高短期負荷的預測準確度.其中user5 的準確度相較其他模型提高得最多,因為user5 的數據波動很大,通過歸一化可以增加數據的穩定性,提高預測的準確度.由表2 可見,不同用戶的MAPE差距很大,這是因為不同用戶的用電行為習慣差異很大.

圖5 為user1 和user8 在2015 年1 月1 日至2015 年2 月28 日的負荷曲線.圖5 中,user1 歷史負荷曲線較平穩,其用電模式較規律,因此可得到較準確的預測結果,而user8 在同段時間的用電行為模式難以捕捉,無法達到較好的預測效果.這說明了針對不同用戶采用不同預測模型的有效性和重要性.

(2)為了驗證聚類方法的有效性,將本文模型與僅輸入相鄰時刻相關的CNN 模型、輸入相鄰時刻序列和日相關特征序列的CNN 模型進行比較,結果如表3所示.

圖5 user1 和user8 2015 年1 月1 日至2015 年2 月28 日負荷曲線

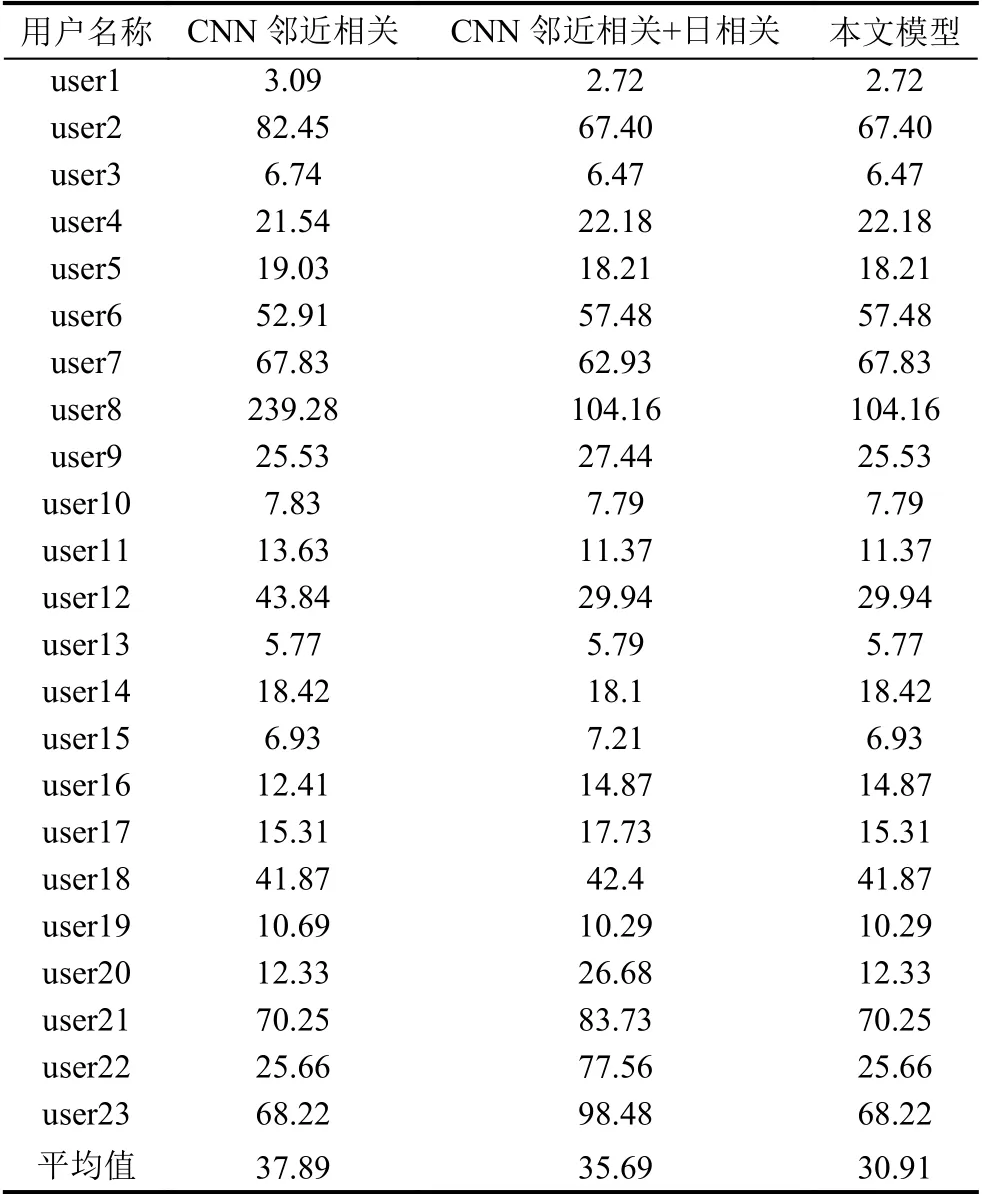
表3 聚類效果MAPE 分析(%)

從表3 不難看出,本文模型的MAPE比簡單將數據放入CNN 模型的MAPE降低了5%,證明了應用聚類算法可更好區別不同用戶的特性,有助于提高預測性能.

5 結論

針對用戶負荷差異明顯、波動性大的問題,本文利用K-means 算法將用戶用電歷史負荷曲線進行聚類,針對不同類別的用戶利用CNN 構造不同的特征提取網絡結構,訓練建立預測模型.實驗結果表明本文模型均比RF、SVR 及未經聚類的CNN 模型的預測效果優秀,預測MAPE降低了21.22%.由于當前預測模型僅參考了用戶的歷史負荷作為模型輸入,實際上用戶負荷與溫度、濕度及用戶所在行業經濟形勢等多種因素相關,后續將考慮篩選更多的相關因素輸入模型中,進一步提高模型的預測準確度.