基于改進粒子群蟻群融合算法的多AGV路徑規劃
熊昕霞, 何利力
(浙江理工大學 信息學院, 杭州 310018)
0 引 言
在當今的制造業中,戰略已從制造大量單個產品轉移到了一系列產品,并改善了質量和交貨時間。許多物流和制造流程都依賴于多AGV系統的使用[1],系統中的每輛車都執行運輸任務,包括在給定的初始位置提取貨物并在所需的目的地進行運輸和卸載[2]。多AGV系統運行效率直接影響整個制造車間的高效運轉。為了改善多AGV系統的運行效率和安全性,要解決的主要問題是正確規劃多AGV的路徑[3]。多AGV路徑最優軌跡是實現基于多AGV智能生產車間的關鍵。
從初始位置到目標位置通過檢測并避開障礙物是自動導引小車在無人倉庫中的最重要功能。因此,在簡單或復雜的環境中工作時,正確選擇導航技術是機器人路徑規劃中最重要的步驟。多AGV路徑規劃是當前研究的一個熱點和難點[3]。張丹露等提出一種基于預約表和動態加權地圖的改進A*算法,應用在多機器人路徑規劃、避障和擁堵問題上[4],改進的A*算法提出預約表與交通規則結合的方式解決了多機器人的碰撞問題,根據生成的動態加權地圖解決了擁堵問題;袁洋等研究多AGV在運行時單個AGV的路徑規劃問題,提出了使用負載均衡改進的A*算法進行路徑規劃的方法,解決多AGV運行路網的局部擁塞、防止和負載均衡問題,將路網負載引入到A*算法的評價函數中,避免多AGV路徑規劃時產生局部車流量過大[5];張毅等根據AGVs剩余電量分配優先級,協調AGVs路徑,以提高小車的使用效率,再使用改進的蟻群算法計算AGVs的最優路徑[3]。
在實際應用中,大多數多AGV路徑規劃研究都是以無障礙、AGV之間的協調、車間不堵塞等路線調整為研究目標,很少將路徑偏差和能源消耗視作關鍵因素。本文提出了一種改進粒子群蟻群融合算法,使每個AGV的路徑長度到達時間最小化。以解決倉庫環境中的多AGV路徑規劃問題。
本文的主要工作如下:第一階段設立目標函數,使每個小車的路徑成本、路徑偏差和能耗最小化。利用混合算法為每個移動機器人規劃出一條最佳路徑;第二階段,障礙物檢測,使每個機器人都避免與障礙物和其他機器人發生碰撞,解決充滿障礙物的倉庫環境中多AGV路徑規劃問題;第三階段,仿真實驗,將獲得的結果與改進的粒子群優化(IPSO)、ACO算法進行比較。
1 問題描述與模型構建
1.1 問題描述與假設條件
在無人倉庫中,為達到目標位置完成運輸任務,要求各個機器人從起點出發,繞過靜態障礙物,并且避免與其他機器人相撞,到達目標位置完成運輸任務。從倉庫中的當前位置計算每個機器人的下一個位置目標。 該路徑的目標是在不與問題沖突的情況下找到最優或接近最優的路徑(最安全、最短和最光滑)。在制定多機器人路徑規劃問題時要考慮以下約束條件。假設:
(1)倉庫地圖已知;
(2)已知機器人的起始位置和目標位置;
(3)每個機器人逐步規劃動作,直到到達各自的目標位置;
(4)機器人到達下一個位置時可能會與倉庫中其他機器人/障礙物相撞。
因此,機器人前進方向將以一定角度向左或向右轉,從而確定其下一個位置。本文提出的混合算法通過假設機器人的當前位置和速度作為優化給定的多目標函數的參數,來評估每個機器人的下一個位置。其確定了動態和靜態環境中從每個狀態到目標狀態的最佳路徑,機器人借助配備的傳感器來測量其到障礙物的距離。
1.2 模型建立

(1)
(2)
當Δt=1時,式(1)、(2)為式(3)、(4):
(3)
(4)

該多機器人路徑規劃問題將作為路徑和能耗都得到優化的問題提出。優化問題被表述為基于約束的多目標函數。目標函數用于表示最小化每個機器人當前位置到其目的地之間的路徑長度,避免與其他機器人和靜態障礙物碰撞的同時優化生成路徑的平滑度。
1.2.1 路徑長度
路徑長度影響機器人的運輸時間,為更快完成任務,通過形成約束f1使得機器人從當前位置到目標位置總路徑長度最小,并且避開障礙物。約束公式為(5):
(5)
將式(3)(4)帶入得到式(6):
(6)
1.2.2 與障礙物的安全距離
為防止機器人與障礙物碰撞,定義了每個障礙物的排斥場,式(7):
(7)
其中,η0是障礙物的影響范圍;k是常數;γ≥2形成電位的徑向輪廓;dmin(Xp)為Xp到障礙物的最小距離。
1.2.3 預測動態障礙物(其他機器人)位置
動態障礙物將動態出現在機器人的路徑軌跡中。因此,在決定下一位置前,機器人需預測動態障礙物的軌跡,式(8):
(8)
其中,(xp,yp)是動態障礙物的預計位置。
1.2.4 路徑平滑度
最小化直線(目標點到建議點)之間的角度差,使得路線平滑度最大,減少機器磨損,提升機器人運行穩定性。路徑平滑度目標函數為式(9):
(9)
第一個函數f1使得每個機器人當前位置到目標位置的歐幾里得距離最小;第二和第三個懲罰函數f2、f3用于避免移動機器人與動態障礙物之間的碰撞;第四個懲罰函數f4是平滑路徑。總目標(適應度)函數為式(10):
fit=λ1f1+λ2f2+λ3f3+λ4f4.
(10)
其中,λ1、λ2、λ3、λ4是4個函數的權重,滿足條件式(11):
λ1+λ2+λ3+λ4=1.
(11)
這些權重在仿真實驗中做出調整,λ1=0.3、λ2=0.3、λ3=0.3、λ4=0.1,通過使用適應度函數最小化來獲取最優路徑。
2 通過蟻群機制中信息素使用改進的粒子群優化
2.1 粒子群優化
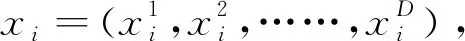
粒子的速度更新:

(12)
粒子的位更新:
(13)
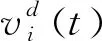
為了更好地控制開發和探索,Shi和Eberhated提出了有關慣性權重的PSO,其中更新了每個粒子的速度,為全局搜索提供更大的慣性權重值,而較小該值將提供局部搜索。為提高PSO的收斂速度,本文將在自適應權重調整和加速度系數方面改進PSO。根據以式(14)和(15)修改:

(14)
(15)
2.2 改進的粒子群優化
PSO的收斂速度借助多種技術對其參數微調而得到了改善。為了避免群里發散而引入慣性權重w,通過調節先前迭代中速度對粒子的定義來控制粒子的速度。因此,當慣性權重值較大時,將實現全局搜索;當慣性權重值較小時,將進行局部搜索。多項研究表明,通過動態改變慣性權重可以提高PSO的搜索能力,而線性遞減慣性權重已經顯示出更好的結果[7]。因此,這里采用慣性權重的自適應方法,如式(16)所示。過去已有實驗驗證,采用組合wmax=0.9,wmin=0.4可以達到最佳性能。
(16)
(17)
max_dist=argmax(disti).
(18)
其中,disti為粒子i與全局最佳粒子之間的歐幾里得距離,如式(17)所示;xgbestd為第d次迭代的全局最優位置;max_dist是一代中粒子與全局最佳粒子之間的最大距離,如式(18)所示。
由于混沌行為類似于隨機性,但具有更好的動力學和統計學特性,與隨機搜索相比,混沌搜索可以更容易地從局部最優解中逃脫[8]。因此,將隨機參數r1、r2替換成一維混沌圖,使得算法收斂速度更快。已有實驗驗證,將隨機參數r1替換成混沌圖獲得的結果最佳,并且Singer映射用于該算法的結果最優[9]。替換后為式(19):

(19)
Singer映射定義為式(20):
(20)
其中,μ是一個0.9到1.08之間的參數。
2.3 蟻群算法
蟻群算法(ACO)是一個受實際蟻群行為啟發的人工系統。在螞蟻搜索路徑過程中,會留下信息素蹤跡,該信息素會隨時間和距離消散。當螞蟻經過下一個位置時,或當更多的螞蟻經過該位置時,該位置上的信息素強度會更高。因此,遵循信息素尾跡的螞蟻將更具以下情況聚集:信息素“濃度”隨著更隨尾跡的每增加一個螞蟻而增加。
在標準ACO中,螞蟻每一步位置轉移按照輪盤賭的方式做出概率選擇,再將信息素沿其蹤跡更新食物來源。t時刻螞蟻k由位置i轉移到j的轉移概率為(21):
(21)
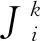
每只螞蟻完成一次搜索后,更新信息素跡線。首先以恒定的蒸發速率降低它們,然后依次使每只螞蟻在其經過的一部分弧上沉積信息素,如式(22):
(22)
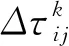
(23)
其中,Lk(t)是行程的長度,Q是固定參數。
2.4 融合改進粒子群優化和蟻群優化算法
由于依賴于外部參數(例如:慣性權重和加速度參數),傳統的PSO算法難以生成最優解,收斂速度較慢。為了解決優化問題,擺脫局部最小值,最大化探索粒子的搜索范圍,通過引入蟻群算法中的信息素協同粒子群優化,如式(24)。
(24)
其中,C3為加速度系數,用于調整IPSO-ACO上的PSO速度。如果C3設置為零,則IPSO-ACO成為獨立的IPSO;如果C3設置為1,則會受到ACO的一半的隨機影響。
信息素軌跡是轉遞到構造圖邊緣的真實值,被視為過程強信息的存儲器,這些信息涉及單個解決方案組件在先前的迭代中的效果。τi-1,i是從點i-1到點i的信息素,對應于一個由吸引力的線連接的兩個點。因此,在混合過程中,IPSO使用內存來保存迄今為止找到的最佳解決方案,通過信息素確認該粒子將被加速。當所有粒子接近良好的解決方案時,移動都非常緩慢,并且gbest可以幫助其充分利用全局最佳方法。每個粒子都觀察到最佳解并向其移動。
3 仿真實驗
3.1 路徑求解流程
本文使用混合算法IPSO-ACO對充滿障礙物的無人倉庫中多AGV進行路徑規劃。在該算法中,從每個AGV的現有位置計算每個AGV的連續最佳位置,同時滿足所有約束并提高收斂速度。使用本文提出的混合算法進行多AGV路徑規劃流程,如圖1所示。
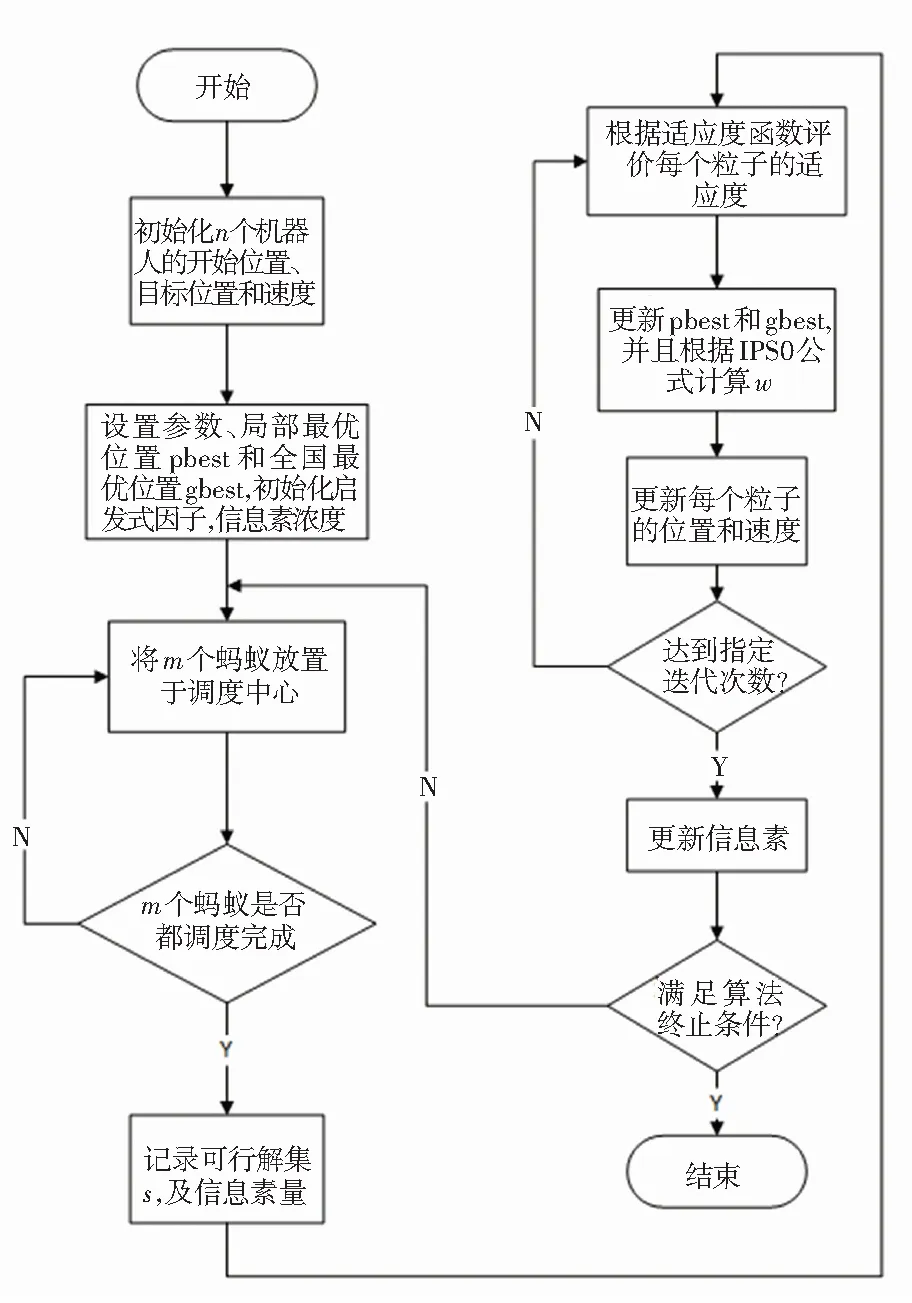
圖1 IPSO-ACO算法流程圖
3.2 靜態障礙物下多機器人路徑規劃
仿真實驗使用Python語言實現,使用圖2作為模擬環境來實現AGV路徑規劃問題。模擬環境中,不同顏色的圓形為每個AGV,正方形為每個AGV對應的目標位置。障礙物隨機分布在模擬環境中。
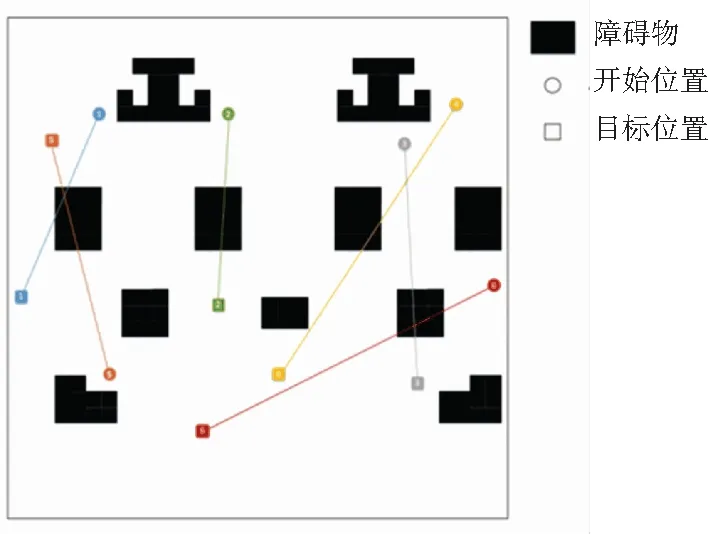
圖2 仿真環境圖
實驗時障礙物和環境是靜止的,其他優先級AGV可以移動。在仿真實驗中設置的算法相關參數見表1。每個GAV根據定義的適應度值來決定其下一個位置。使用IPSO-ACO算法使每個AGV到達其相應位置,虛線表示每個AGV的路徑,如圖3所示。從圖3中可知,6臺AGV都分別到達了目標位置,第3臺和第5臺AGV在第13步時距離非常接近,在路段上可能發生沖突,第3臺將第5臺AGV視作動態障礙物,重新計算其路徑,避開動態障礙物。
3.3 算法比較
為評估IPSO-ACO的性能,運用IPSO和ACO算法在上述環境中對6臺AGV進行路徑規劃,算法相關參數設置與IPSO-ACO相同。AGV通過三種不同算法到達其對應目標位置所需的時間進行了比較,其折線圖如圖4所示。由圖4可知使用本文算法為所有機器人到達目標規劃的路徑比其他兩種算法每步所需時間更短。圖5顯示了三種不同的啟發式算法的每一步的目標距離對比,與IPSO和ACO相比,使用IPSO-ACO算法到達目標位置的距離最短,且最終的路徑長度以及所需步數都較小。
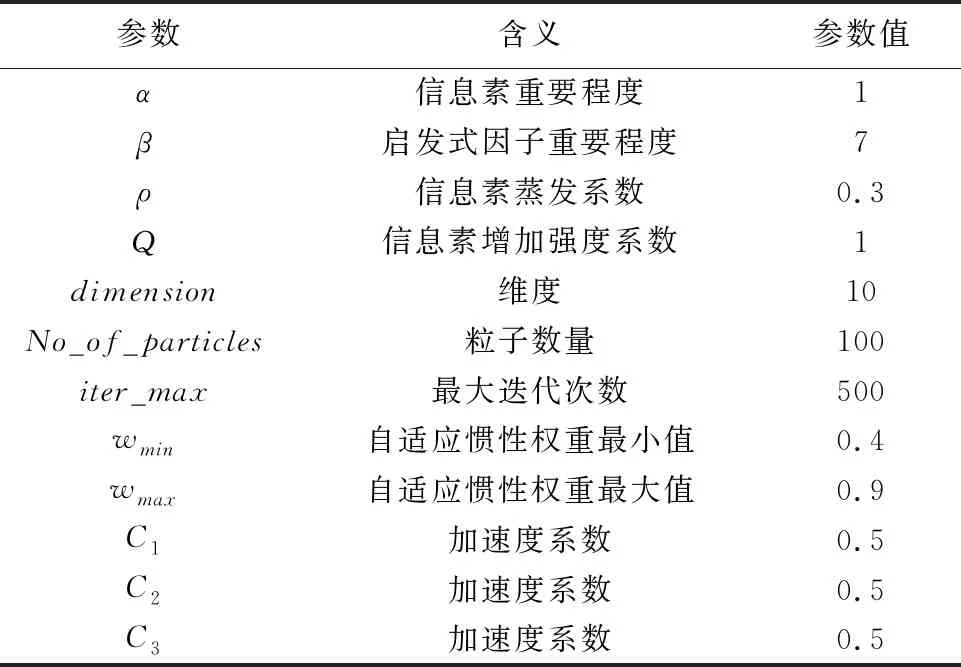
表1 算法相關參數
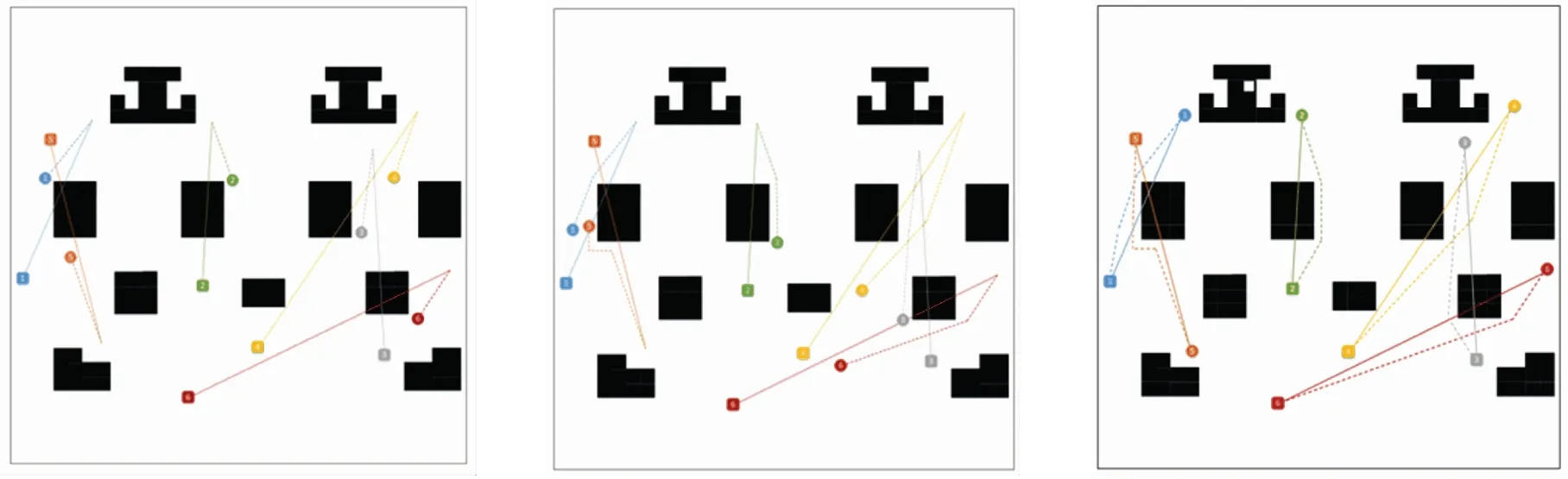
(a) 第7步結果 (b) 第13步結果 (c) 第19步結果
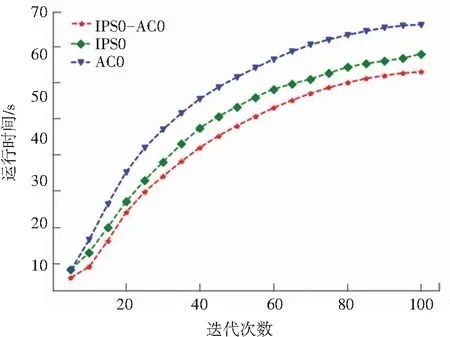
圖4 三種算法迭代次數和運行時間
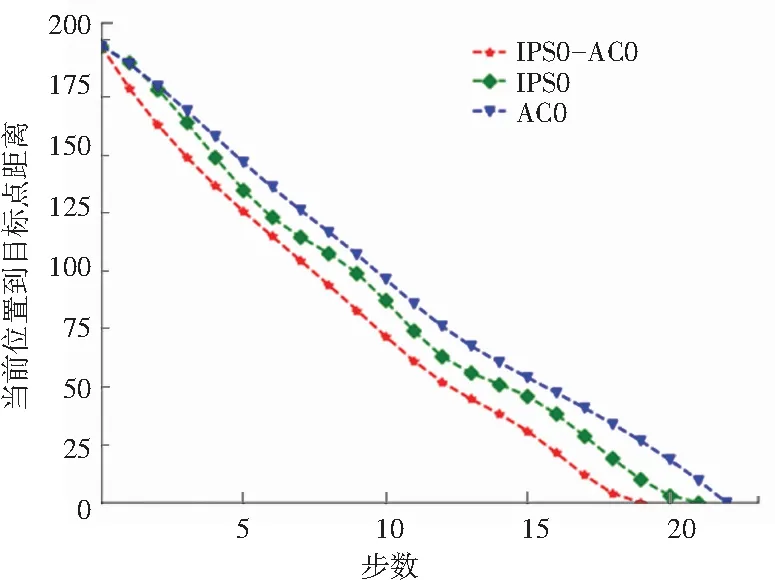
圖5 三種算法的步數和平均目標距離
4 結束語
本文提出了一種改進粒子群蟻群融合算法,以提高粒子群優化算法的搜索能力,避免陷入局部最小值,實現更好的收斂性。使用該混合算法解決充滿障礙物的無人倉庫中多AGV路徑規劃。通過軟件模擬,并與IPSO和ACO算法對比,該方法的效率更高,優化效果更好。

