基于高斯核層次聚類的汽車工況構建

韓 鑫

(西安石油大學 計算機學院， 西安 710065)

0 引 言

汽車行駛工況也被稱為車輛測試循環，描述了汽車行駛速度的時間曲線(通常在1 800 s以內)，反映了道路上汽車的運動特性[1]。其是汽車工業中重要且常見的基本技術、車輛的能耗排放測試方法和極限標準的基礎，也是汽車各種性能指標的校準和優化的最重要基準。中國幅員遼闊，不同城市之間的發展程度、氣候條件和交通條件的差異，使各個城市的駕駛條件特征明顯不同。因此，作為車輛開發和評估的基礎，越來越需要從城市自身的駕駛數據中進行汽車行駛工況構建的研究。

大多數已有研究在工況構建時選擇k-means 聚類方法作為聚類手段[2]，但由于k-means 聚類需要提前確立數據中聚類的個數k。根據已有的研究結果及經驗，將類別分為 3 類或者4類[3]。然而，當數據量較大，采集數據情況復雜時，先驗知識具有很大的局限性[4]。在不觀察數據就確立類別數，勢必會給聚類結果帶來很大的誤差。層次聚類算法可以返回一顆聚類樹，從聚類樹中可以得到所有的聚類結果供使用者選擇，從而避免了選擇聚類個數的問題。由于一般汽車工況特征比較復雜，極有可能導致數據在低維空間下不可分，而使用核方法特別是高斯核方法，可以將數據特征空間映射到高維甚至無限維的空間，從而更好地將數據分開[5]。因此，本文采用基于高斯核的層次聚類算法，對構建的車況特征進行聚類，提高聚類準確度。

1 特征定義

將收集的速度數據轉換為特征參數數據的過程，可以視為數據轉換。特性參數可以更好地表達短途行駛的情況，并且更有利于分析。在分割的短行程中只有速度和時間數據，但是僅使用速度和時間并不能完整地表征短行程運行的特征。因此，本文從統計信息、形狀信息以及熵信息中共提取構建了21個特征。

1.1 統計特征

短行程的統計特征數據主要為速度、加速度的比例、均值、標準差、最大最小值等，速度與時間數據是直接采集的。由于采集頻率為1 HZ,所以對于任意時刻i,則有ti+1-ti=1, 加速度計算如式(1)所示：

(1)

其中，ai,i+1為第i秒到第i+1的加速度，m/s2;vi為i秒的速度,km/h;ti為第i秒時刻，s。

(1)最大速度、平均速度、速度方差(vmax,vm,vme,vsd)的計算公式分別為：

(2)

(2)最大加速度、最小加速度、平均加速度、平均減速度、加速度方差(amax,amin,aa,ad,asd)的計算公式分別為：

(3)

其中，Ta為加速度大于0.15的時間；Td為減速度小于0.15的時間。

1.2 形狀特征

除構建統計特征外，由于片段為時間序列，需要捕獲速度在波形形狀上的特征。最新研究表明，將偏度和峰度相結合是對序列相關性度量的有用特征。偏度是統計數據分布中偏斜方向和程度的度量，是統計數據分布中偏斜度的數值特征。峰度表示概率密度分布曲線的峰值在平均值處高度的數量特征。直覺上，峰度反映了峰的銳度[6]。

對于長度為T的時間序列XT={x1,…,xT},其均值μ和方差σ分別為：

(4)

(5)

T的偏度定義為其三階標準化矩為：

(6)

T的峰度定義為其四階中心矩與方差平方的比值:

(7)

1.3 序列熵特征

除構建片段統計特征和形狀特征外，還需要描述片段的確定性或者穩定性。在本文中，對于速度片段的時間序列，加入Binned 熵和Approximate 熵用于分別度量速度片段的均勻性和穩定性。

Binned熵考慮將時間序列XT的取值進行分區操作。之后計算時間序列的取值分散在所有區域中的概率分布的熵。

(8)

其中,pk表示時間序列XT的取值落在第k個桶的比例(概率)；maxbin表示區域的個數；len(XT)=T表示時間序列XT的長度。

片段速度序列的 Binned 熵越大，說明這一段時間內速度取值的分布，在[min(XT),max(XT)]之間越均勻。如果一個片段的速度序列的 Binned 熵值較小，說明這一段時間序列的取值是集中在某一段上。

Approximate熵是為了判斷一個序列是隨機出現還是具有某種趨勢。其基本思想是，把一維空間的時間序列映射到高維空間中，并通過高維空間向量之間的相似度判斷，推導出一維空間的時間序列是否存在某種趨勢或者確定性。

ApEn(m,r)=Φm(r)-Φm+1(r).

(9)

其中，Φm(r)為一個m維的函數。

2 基于高斯核的層次聚類

層次聚類是一種常見的聚類算法，該算法能在不同的層次上對數據樣本進行劃分歸類，而不需要提前確定聚類的類別的數量。同樣，該算法適用于對樣本不確定或缺乏領域知識時使用。通常，層次聚類可分為兩種特定的策略。一是：將樣本(小類)從底部到頂部(大類)進行分組的策略；二是拆分型層次聚類：將大類從頂部進行劃分。根據研究對象及數據的具體情況，本文采用第一種凝聚型層次聚類策略。

凝聚型層次聚類的具體步驟，是將每個樣本視為具有單個元素的單個聚類，然后計算類之間的距離(相異性)，合并具有最短距離的類(即最大的相似性)，并遍歷整個過程，逐步將小類合并，直到所有樣本都在同一類中為止。設給定n個樣本點x1,x2,…,xn，具體流程如下：

(1)將每個樣本點視為一個類，并計算兩個樣本之間的距離dist(xi,xj)；

(2)將兩個最接近的類，合并為一個新類；

(3)更新類間的距離；

(4)重復(2)和(3)步驟，直到所有樣本都被合并到一個類中/達到結束條件為止。

從層次聚類算法流程中可以看出，凝聚型層次聚算法的關鍵問題是，確立對象(樣本)間，以及簇與簇之間的距離。而類與類之間的距離是根據不同的連接函數(如單連接、全連接)從樣本間的距離產生。因此，兩兩樣本之間的距離在算法中發揮著重要作用。在計算兩個樣本之間的距離時，傳統的層次聚類法往往采用歐式距離。對于樣本xi和xj，其距離度量如式(10)所示。

dist(xi,xj)=‖xi-xj‖2.

(10)

然而，基于歐式距離的凝聚型層次聚算法受噪聲點的影響較大。當兩個類的距離較近時，會由于少量距離較近的點優先合成一個簇，而實際兩個類的大多數樣本并不接近，從而造成聚類誤差。基于歐式距離的凝聚型層次聚類算法，可看做是使用線性模型學習決策邊界，由于它只能學習非常簡單的線性決策邊界，因此造成該算法對噪聲點非常敏感，從而無法將類別有效的分開。對于在線性空間中無法分開的情況，可以將數據提高維度，在高維空間中找到分類邊界，進而避免噪聲點在原始空間的影響[5]。

本文采用高斯核度量的方法實現維數的增加，其定義如下：

(11)

如式(12)所示，高斯核函數的特性是把低維空間轉化為無限維空間，同時又實現了在低維計算高維點積。

k(x,y)=〈φ(x),φ(y)〉=e-σ‖x-y‖2=e-σ(x2+y2)eσ2xy=

(12)

若給定n個樣本點x1,x2,…,xn，基于高斯核的凝聚型層次聚算法如下：

(1)將每個樣本點視為一個類，并基于式(11)計算兩個樣本之間的距離；

(2) 將兩個最接近的類合并為一個新類；

(3)更新類間距離；

(4)重復(2)和(3)，直到所有類都被合并到一個類中/達到結束條件為止。

從高斯核凝聚型層次聚類算法流程可以看出，該算法將樣本間的距離計算修改為基于高斯核函數的度量，其它則保持了原始算法的步驟。該算法在保證了原始層次聚類算法簡單性的同時，又可提高算法在克服線性不可分情況的缺陷。

3 實 驗

原始采集數據經過運動學片段的劃分、篩選，采用基于高斯核的層次聚類結果，使用TSNE在二維空間中可視化的展示如圖1所示。 所有運動學片段可被分為3個類別，但每個類別中仍然有數百個運動學片段，則可從每個類別中提取適當的片段，這些片段應該盡可能完整地反映每種類型的片段特征，從而使構造的車況曲線可以客觀地反映車輛的實際駕駛情況。

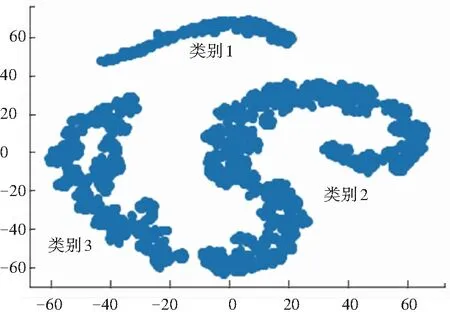
圖1 聚類結果圖

通過分析每一類的運動學片段發現：第一類的加速、減速時間比例最低，怠速時間比例最高, 說明汽車長時間怠速，但是起步加速與制動減速運行時間較短，第一類可代表汽車在擁堵的主干道上的交通特征；第二類的加速、怠速、減速時間比例均中平，勻速時間比例最高，表明汽車勻速行駛時間較長，同時也要經歷一定的停車、怠速、起步，第二類可代表汽車在比較暢通的支干道上行駛的特征；第三類的勻速、怠速時間比例最低，加速、減速時間比例最高，代表汽車行駛中可以長時間加速、減速行駛，停車怠速時間很短，該類可代表汽車在通暢的城郊道路上行駛的特征。

從每個類中挑選運動學的一個片段，拼接成1 300 s的工況循環曲線，如圖2所示。

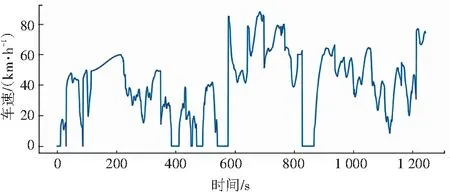
圖2 構建工況圖

由此可見，其結果完全符合汽車工況規律，具有有效性。

4 結束語

汽車行駛工況描述了汽車行駛速度的時間曲線，反映了道路上汽車的運動特性，是車輛的能耗排放測試方法和極限標準的基礎，是汽車各種性能指標的校準和優化的最重要基準。本文在定義了包括統計特征、形狀特征、熵特征等共計14個運動學片段的有效特征后，構建基于高斯核的層次聚類算法對片段進行聚類。 根據運動學片段類別的比例及

時間比例，從聚類結果的中抽取具有代表性的片段拼接成1 300 s的工況圖。經試驗結果表明，構建的工況圖具有較大參考價值。