長短期記憶神經網絡在葉綠素a 濃度預測中的應用

石綏祥，王蕾,2*，余璇，徐凌宇

( 1. 國家海洋信息中心 數字海洋實驗室，天津 300171；2. 國家海洋局東海信息中心，上海 200136；3. 上海大學 計算機工程與科學學院，上海 200444)

1 引言

葉綠素a 濃度作為水質狀況及富營養化程度的衡量指標，一直是水質監測的重要參數[1–3]，是判斷赤潮發生與否的重要因素，因此越來越多的科研人員投入到對葉綠素a 濃度的預測研究中。而限于早期葉綠素a 濃度相關數據的匱乏，對葉綠素a 濃度的預測大致可以分為兩類方法，其中一類方法為統計學方法，這一類的方法最先由加拿大專家Vollenweider[4]提出，他利用了統計模型來預測富營養化問題，但是這一類傳統的統計方法只能求解某一要素的平均濃度分布，無法模擬相關因素與葉綠素a 的影響關系；另一類方法主要是以生態動力學為理論依據，基于對流?擴散方程建立模型[5]來預測葉綠素a 濃度，此類方法的優點是考慮了自然界中多種因素間的相互作用，但生態動力學模型有一個共同的缺陷是其包含太多參數，而這些參數的設定十分依賴對于特定問題的經驗，并且難以確定合適的參數。

隨著數據量和種類的增多，收集的數據也越來越多，傳統的統計學習方法越來越難以適應，鑒于神經網絡及深度學習在大數據量及復雜場景中，對于特征的表達能力，越來越多的學者開始利用神經網絡及深度學習對葉綠素a 進行預測。人工神經網絡是一種模擬生物神經網絡信息處理功能的信息處理模型，也是一個高度復雜的非線性動力學系統[6]。在此類研究中，最具代表性的人工神經網絡模型是反向傳播神經網絡(Back Propagation Neural Network, BPNN)，趙玉芹等[7]利用BP 神經網絡成功地對渭河水質參數進行了遙感反演；盧志娟等[8]利用BP 神經網絡實現了對西湖湖心區葉綠素a 濃度的周預測；周露洪等[9]通過對2006?2008 年的常規水質參數進行主成分分析，建立BP 神經網絡模型對葉綠素a 濃度進行月預測；楊柳等[10]利用BP 神經網絡對溫榆河進行了水質參數反演，反演結果優于傳統線性回歸模型。應用廣泛的BP 網絡大多只考慮相關因素對葉綠素a 的影響關系，而忽略了所有影響葉綠素a 的因素在不同時延上影響關系的差異性，無法動態的依賴歷史時序信息進行葉綠素a 濃度預測，并存在局部極小、收斂時間過長從而泛化能力差的問題[11]。

Dekker 等[12]建立了葉綠素a 濃度與TM 影像的線性和指數回歸模型，指出指數模式要優于線性模式，但TM 的分辨率較低，不利于水質參數監測，且T 的波段組合缺乏物理解釋；柴永強等[13]利用決策樹模型智能檢測赤潮現象，采用機器學習技術訓練檢測赤潮的決策樹分類模型，此模型對渤海等海域取得了較滿意的結果，但是決策樹模型對缺失數據處理比較困難，也容易出現過擬合現像；李修竹等[14]采用支持向量機的方法，以溫度、鹽度等8 種要素作為輸入，葉綠素a 濃度作為輸出對葉綠素a 濃度進行預測取得了較好的結果，此種方法雖然避免了神經網絡方法的局部極小值問題，但是對核函數的高維映射解釋力欠缺。

基于目前的研究成果，本文在海洋數據多要素關聯關系的基礎上，提出了一種結合時序方法的遞歸神經網絡智能預測模型，對判斷藻類赤潮的重要指標葉綠素a 濃度進行預測，以解決傳統的遞歸神經網絡的梯度消失或爆炸問題。

本文的創新點主要集中在兩個方面：（1） 量化不同要素對于葉綠素a 濃度在不同時延上的關系，依據長短期影響關系將其分類；（2） 對于不同的類別要素，構建差異性的子網絡對其分別建模，每個子網絡采用不同的訓練方式，利用融合層將不同子網絡的特征進行融合以得到更為穩定準確的結果。

2 數據來源與研究方法

2.1 數據來源

近年來，三都澳水產養殖的開發利用幾乎是直線上升，宜養面積的利用超過100%，由于三都澳是一個口小腹大的內灣，一般海水進行一次完全循環要1 周，垃圾在海面上漂流很長時間，沉積慢，嚴重影響了海區環境衛生，影響海區水交換，使水域污染日益嚴重，超過水域的自凈能力，導致海水富營養化加劇，病害發生頻繁，因此本文選取三都澳的連續監測資料作為本文的實驗數據，其中三都澳站位數據時間段是從2015 年5 月12 日至2015 年7 月2 日，監測要素包括表層溫度（WD）、PH、電導率（DDL）、葉綠素（YLS）、濁度（ZD）、溶解氧（RJY）、鹽度（YD）、電壓（DY）共8 個，監測頻率的時間間隔為5 min 一次，站位分布情況如圖1 所示，圖中紅色位置是三都澳站點所在位置。

2.2 研究方法

本文利用長短期記憶（Long Short-Term Memory,LSTM）模型強大的長短期記憶能力分析三都澳站位水質監測數據，選擇對三都澳水質影響較大的因子網絡模型，預測三都澳站位的葉綠素a 濃度的變化趨勢，從而為有效及時地控制水質提供科學依據，總體研究方法由圖2 所示。

從圖2 中可以看出本文提出的模型一共分為3 層：數據分析層、模型層和決策層。其中數據分析層為原始數據的預處理，第二層模型層包含自相關性分析、多要素與葉綠素a 的關聯關系分析、長短期依賴時間分析以及構建融合的LSTM 預測模型，第三層通過對預測分析結果的反饋來提供的有效分析決策。

3 數據預處理

3.1 數據歸一化方法

由于各要素原始數據的量綱及數量級不同，在進行數據相關性分析和網絡訓練前要先對數據進行歸一化處理。

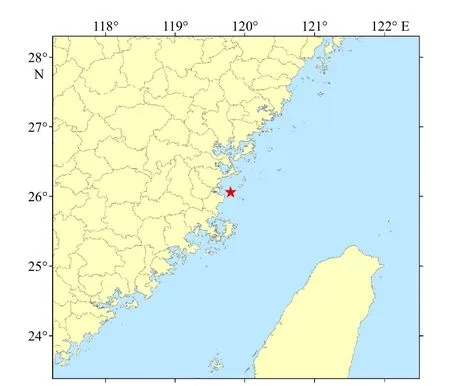
圖 1 三都澳站位分布Fig. 1 Station location distribution map of Sandu Ao

經過標準化處理后的數據一般在0 到1 之間，這樣有利于網絡訓練，在量綱統一的基礎上為下一步相關性分析和網絡訓練奠定基礎。

3.2 自相關分析方法

在進行葉綠素a 濃度預測前，首先需要知道葉綠素的自相關情況，以便在后面的網絡訓練和預測過程中如何考慮其自相關情況。

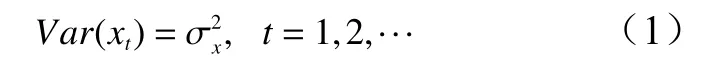
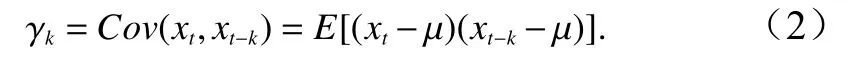
相隔 k 期的兩個變量 xt與 xt?k的協方差即滯后 k期的自協方差可以定義為：程的自協方差函數。當 k =0 時， γ0=Var(xt)=自相關系數的定義如下：

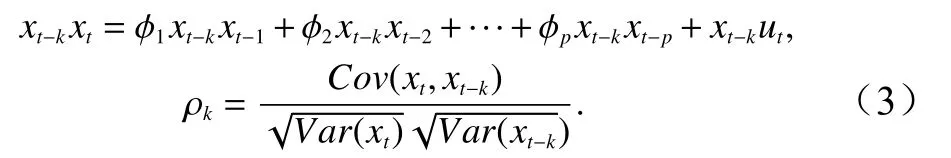
4 構建融合的（Merged）LSTM 模型

4.1 多要素間關聯分析方法

m×n

散布矩陣為 的半正定矩陣如下：

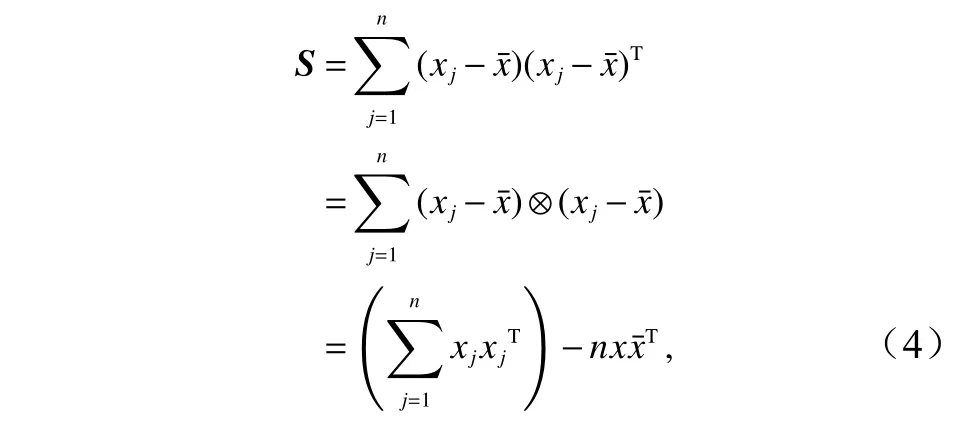
其中 T 表示矩陣的轉置，散布矩陣可以簡要的表示為S=XCnXTCnXT，在此 Cn定 義為定心矩陣，其中 Cn公式如下：

式中，O 表示所有元素都是1 的矩陣；在最大似然估計中，給定 n個樣本，一個多元正太分布的協方差可以表示為歸一化的散度矩陣：

4.2 長短期依賴時間分析法

X 、 Y （也可以看作兩個集合），它們的元素個數均為N （ N 表示時間序列的長度），兩個要素取的第i(1 ≤i ≤N)個值分別用 Xi、 Yi表示。對 X 、 Y進行排序（同時為升序或降序），得到兩個元素排行集合 x 、 y ， 其中元素 xi、

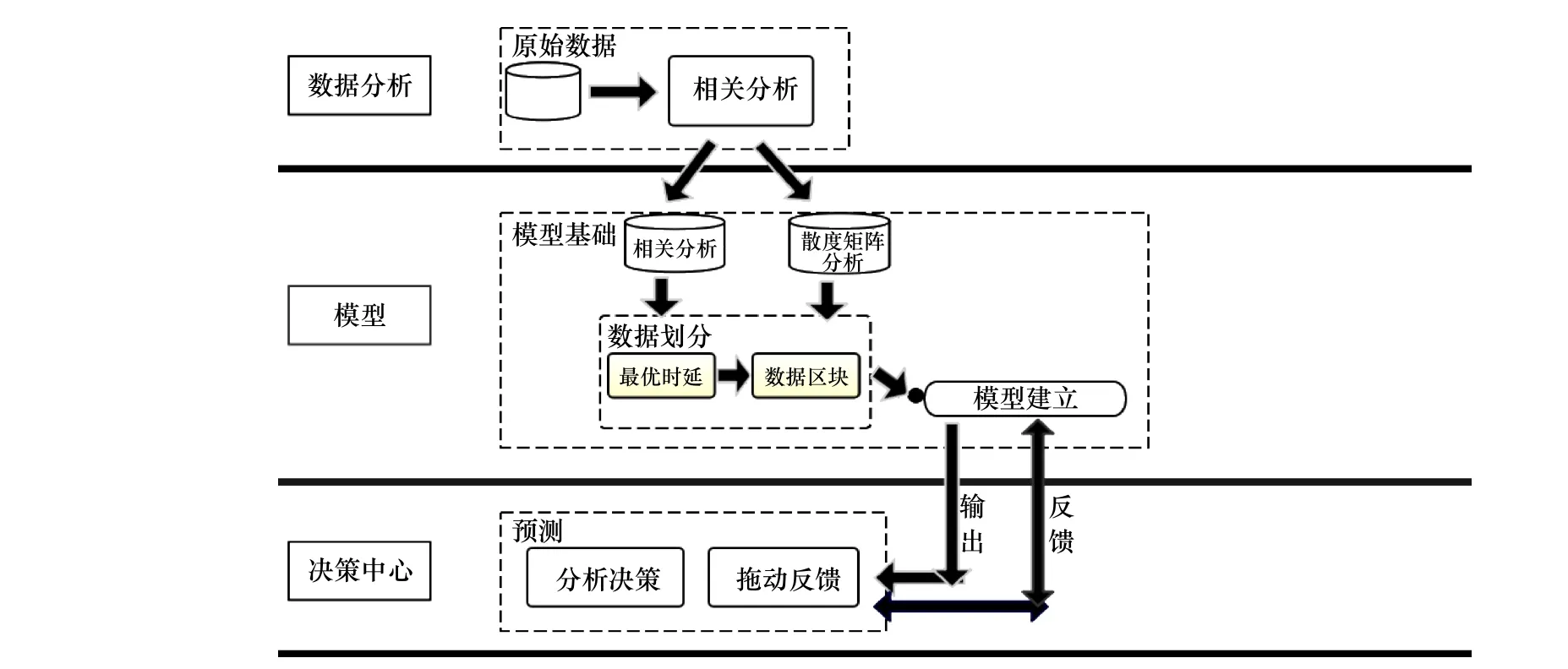
圖 2 研究方法圖Fig. 2 Research method map

本文對不同海洋要素間關系采用相關系數方法計算出不同時間延遲下的相關系數大小，確定最優時間間隔，相同時間間隔的作為一個整體劃分。對于葉綠素a 要素與其他任意一個要素的時間序列定義為yi分別為 Xi在 X 中的排行以及 Yi在 Y中的排行。將集合x 、 y中 的元素對應相減得到一個排行差分集合d，其中di=xi?yi， 1 ≤i ≤N 。隨機變量 X 、 Y之間的斯皮爾曼等級相關系數可以由x 、 y或 者 d計算得到，其計算方式如下所示

相關關系是一種非確定性的關系，相關系數是研究變量之間線性相關程度的量。我們將相關系數定義為：

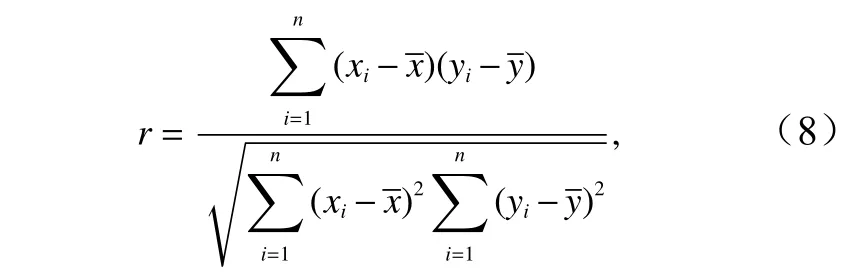
4.3 LSTM 神經元

LSTM 由Hochreiter 和 Schmidhuber(1997)提出[15–16]，隨后Alex Graves 對算法進行了改良和推廣[17]，基于改進的LSTM 相關網絡結構得到了廣泛的應用。例如，文獻[18]將降雨量的預報作為一個時空序列預報問題，應用LSTM 結合CNN 來預測一個地區在相對較短時間內的未來降雨強度；文獻[19]將海水海表面溫度（Sea Surface Temperature, SST）預測作為一個序列預測問題，建立了一個端到端可訓練的LSTM 神經網絡模型，從時空角度利用歷史數據預測未來的SST 值，各像素的局部相關性和整體性可以通過固定尺寸的板塊來表達和保持。LSTM 通過遺忘門和輸出激活功能的設計來處理信息的長短期記憶，其神經元結構如圖3 所示，它包含一個動態的門機制，由輸入門、輸出門、遺忘門和記憶單元組成[20–22]。

圖4 詳細的描述了LSTM 內部的數據流，其中遺忘門讀取上一個狀態 h _(t ?1) 和 當前輸入狀態 x_t的信息，通過 S igmoid層輸出一個在0 到1 之間的數值給每個細胞狀態 C_(t ?1)，C _(t ?1)中的數字決定從細胞狀態中丟棄什么信息，1 代表“完全保留”，0 代表“完全舍棄”。我們通過輸入層來決定什么樣的新信息將被更新并且放在細胞狀態中，首先將 h_(t ?1) 與 x_t輸入Sigmoid 函數確定將要更新的值，然后通過 t anh 層創建候選值向量隨后將舊狀態與 ft相乘，確定我們需要遺忘的信息，加上與的乘積產生新的候選值，最終我們根據新的細胞狀態來決定輸出什么值，通過Sigmoid 層決定輸出的細胞狀態，將細胞狀態通過tanh層進行處理并將其與 Sigmoid的輸出相乘得到這一時間的輸出，可以形式化的描述如下：

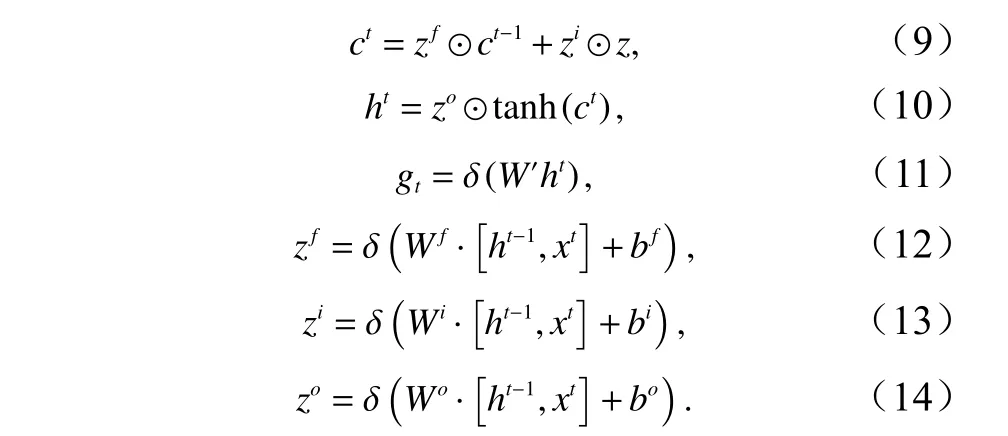
4.4 Merged-LSTM 時間序列學習結構

根據前面數據分析結果構建融合的LSTM 時間序列學習模型，模型結構如圖5 所示。模型的輸入數據分為兩類，其中第一類是根據4.2 節長短期依賴時間分析方法得到的短期依賴要素，標記為OS，即在5 d 內相關系數相似的因素類，另一類是根據長短期依賴時間分析方法得到的長期依賴要素，記為BS，即在5 d 到15 d 時間內相關系數相似的因素類。如圖5所示，從模型的第二層開始，我們分別對BS 和OS 兩類不同的依賴關系要素采用不同的結構進行訓練，其中一個用于訓練OS 序列，使用一層的LSTM 來進行短期依賴記憶；另一個用于專門訓練BS 的時序依賴關系，使用兩層的LSTM 來進行長期依賴記憶，之后使用一層Merge Layer 將兩類經過LSTM 訓練之后的數據合并起來，最后將輸出數據送入Rectified Linear Units 進行激活，以便達到更快的收斂速度，最后通過輸出層Linear 線性輸出[23]得到最終預測結果。

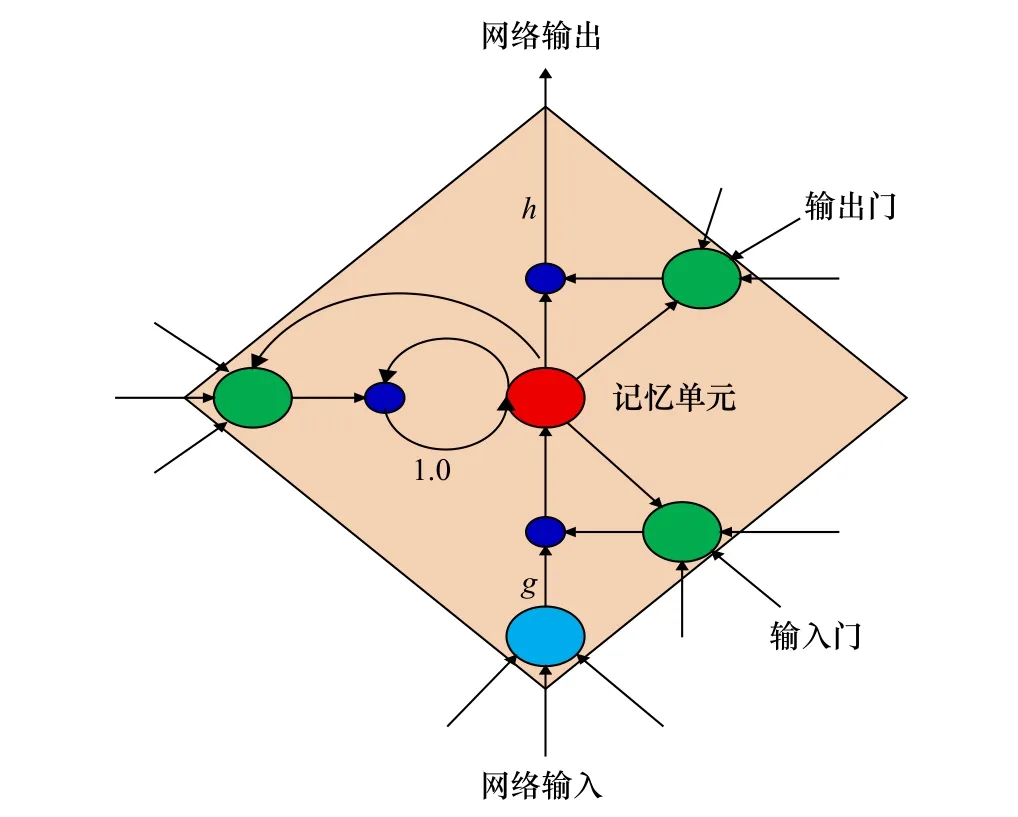
圖 3 LSTM 神經元結構Fig. 3 Neuron Structure of LSTM

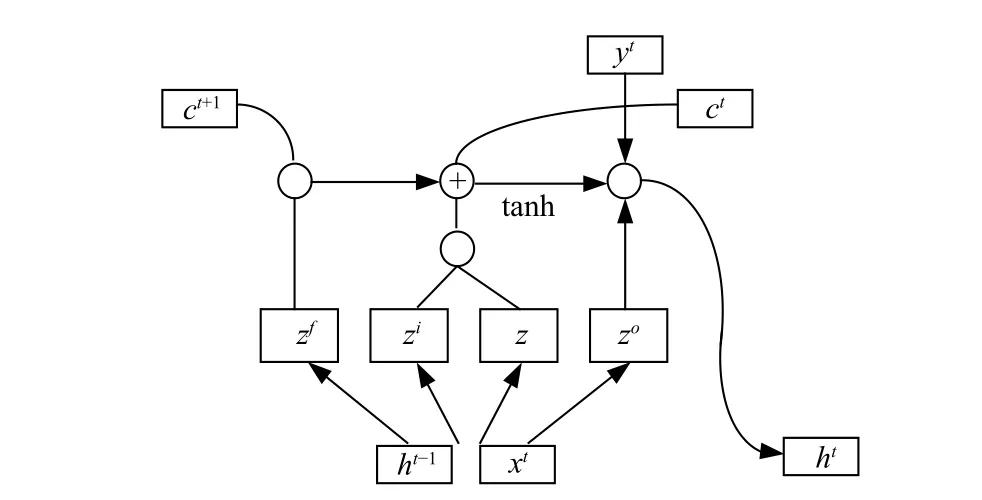
圖 4 LSTM 內部計算流程圖Fig. 4 LSTM internal calculation flow chart

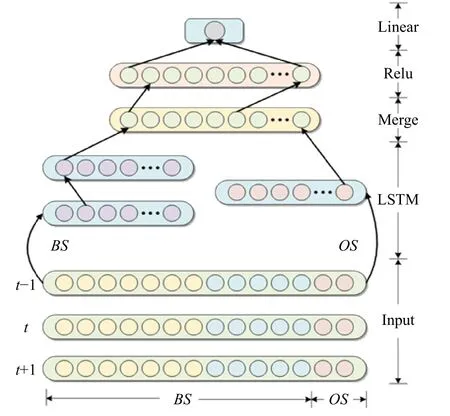
圖 5 Merged-LSTM 結構圖Fig. 5 The structure of Merged-LSTM

網絡采用如下交叉熵公式：

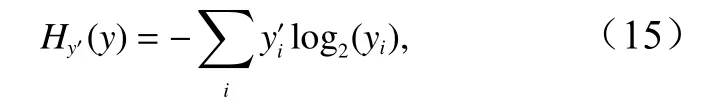
其中 y 是我們預測的分布， y′是真實的分布，交叉熵作為指標來衡量模型的預測用于描述真相的好壞，在這里我們通過梯度下降方法最小化交叉熵來使模型的輸出更符合真實分布。

5 實驗結果與分析

本文采用2.1 節的數據源去除無效數據，然后對數據進行歸一化和自相關性分析，然后利用多要素間關聯分析方法得到要素之間的關聯關系如圖6 所示。

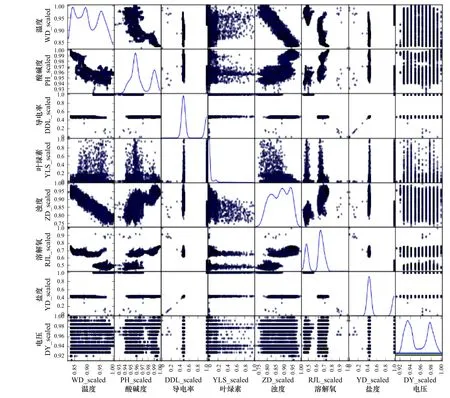
圖 6 要素間相似矩陣圖Fig. 6 Similarity matrix diagram between elements

圖6 的每一個小圖都表示任意兩個要素之間的相關程度，其中對角線所示的子圖為每個要素的自相關曲線，我們可以觀察葉綠素a 與其他各要素之間的關系。從圖中可以看到，葉綠素a 與其他要素間的相關散布矩陣多呈現有規則的點云形狀，形狀越規則，相關性越強。從分析結果可以看出各個屬性與葉綠素a 之間都存在一定的相關性，因此本文選取全部8 個要素作為預測葉綠素a 濃度的基礎數據。

根據選取的所有要素，利用長短期依賴時間分析法計算出其他要素與葉綠素a 濃度在不同時延下的相關系數，見表1 所示。

表1 為葉綠素a 濃度與各個要素在不同時延下的相關系數，每一列代表5 個數據的時延關系，根據計算出的相關系數，我們可以把采集到的不同維度進行分類，在本文中把相關系數絕對值0.2 以下的定義為短期依賴關系，0.2 以上的定義為長期依賴關系，這樣可以把這8 個要素劃分為兩類，一類是與葉綠素a 濃度具有長期依賴關系，另一類與葉綠素a 濃度具有短期依賴關系。不同的依賴關系分別用不同的神經網絡單元及層數訓練，然后在融合層進行信息融合，為模型建立提供依據。

本文模型中OS 子網絡中，每個隱藏層LSTM 神經元個數設置為64，BS 子網絡中，每個隱藏層LSTM神經元個數設置為128，參數利用隨機正態分布進行初始化，初始學習率設置為0.01，學習率按照lrt=lr0/(1+kt)進行遞減，其中 k為控制減緩幅度， t 為訓練次數，本文中 k 設置為0.005。訓練集數據為樣本數據的70%，驗證數據集為樣本數據的30%，由圖7 可知誤差下降速度較快，在訓練次數為300 次時基本達到收斂，并且在下降過程中沒有出現劇烈的抖動，表明本文所提出的模型結構具有收斂速度快和訓練穩定性高的優點。

我們對比了本文所提出的模型與傳統的多元線性回歸(Regression)，多層感知器(Multi-layer Perceptron, MLP)以及遞歸神經網絡(Recursive Neural Network, RNN)對葉綠素a 濃度的預測結果，圖8 為實驗對比分析圖，其中橫坐標為時間點的個數，共30 個時間點，每個時間點相差5 min，縱坐標為歸一化后的葉綠素a 濃度值。圖9 為實際葉綠素a 濃度值和預測葉綠素a 濃度值的真實誤差對比，從圖中可以看出這組實驗在預測誤差方面本文方法比以上所提的4 種方法低很多。

我們通過計算不同方法的平均誤差發現，本文所提出的模型在實驗中誤差結果別為0.11，取得了最好的結果。傳統的多元線性回歸的誤差結果為0.48，優于多層感知器模型MLP 的誤差結果0.49，遞歸神經網絡的誤差結果0.16，優于傳統的多元線性回歸的平均誤差結果。綜合以上分析，我們發現考慮不同要素在不同時間點之間的內部關系，對葉綠素a 濃度的預測結果準確性可以得到大幅度的提升，其次由于遞歸神經網絡將要素間的長短期依賴關系看做相同的整體，因此其預測誤差比本文所提出的模型大。同樣的，這也表明我們不能簡單的將多要素的信息看做一個整體，而是需要先對各要素間的長短期依賴關系進行分析，再依據分析結果設計合理的網絡結構。

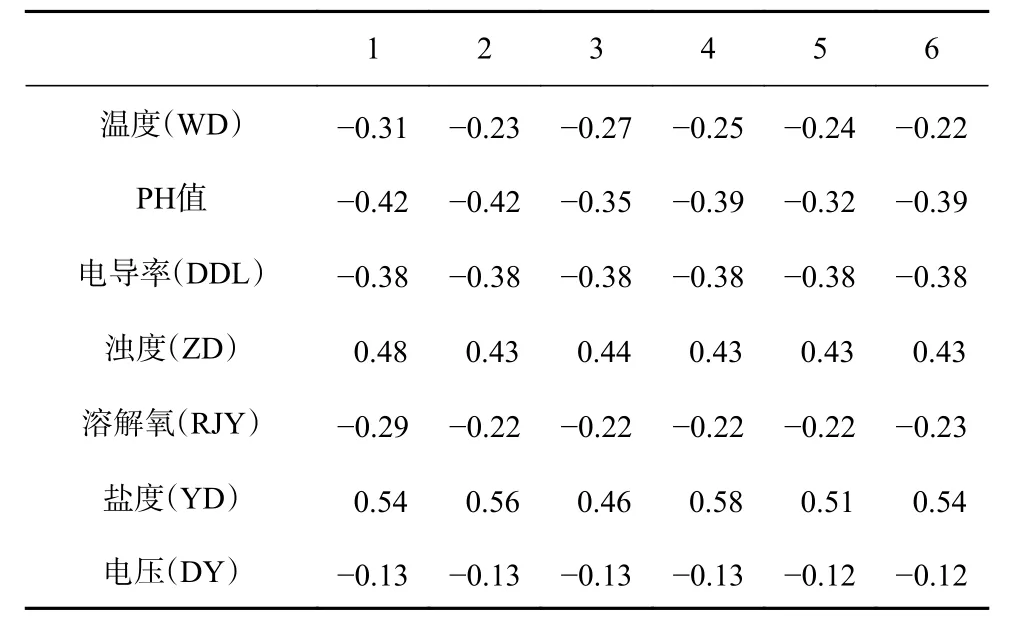
表 1 不同時延下相關系數Table 1 Correlation coefficient under different time delays

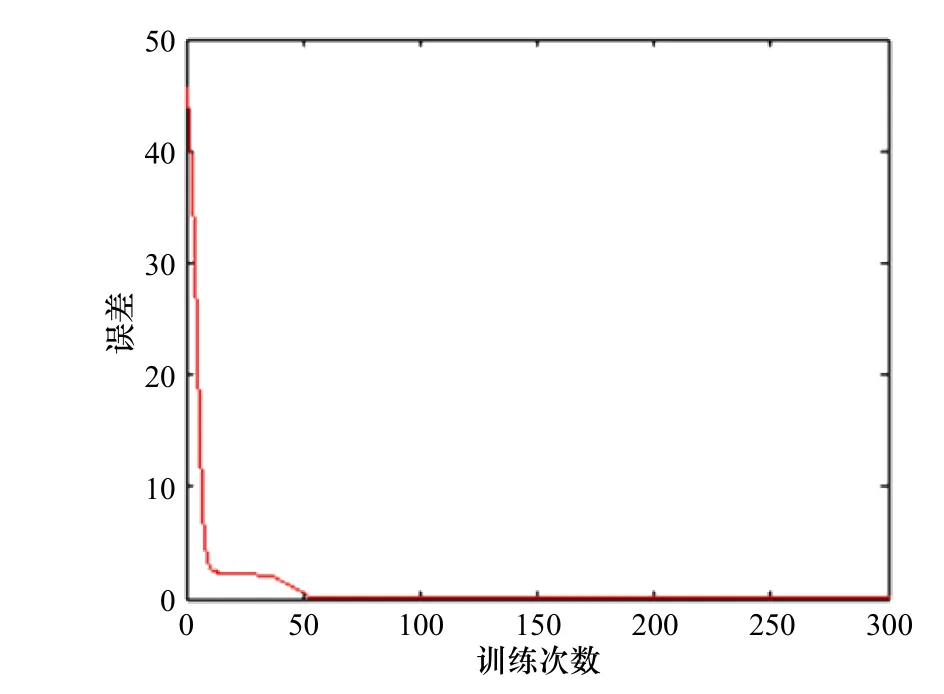
圖 7 模型訓練誤差下降情況Fig. 7 Decline of model training error

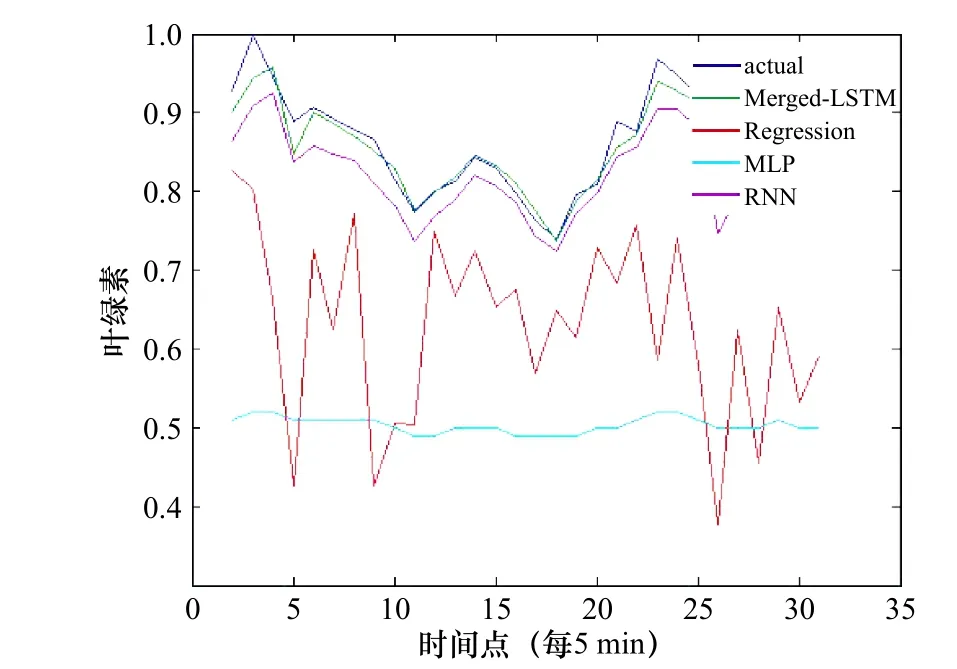
圖 8 實際葉綠素a 濃度值和預測葉綠素a 濃度值Fig. 8 Actual and predicted chlorophyll a concentration

6 結論

本文考慮到多要素與葉綠素a 濃度之間的關聯性，再加上多要素與葉綠素a 濃度的長短期依賴關系，并結合長短期記憶的人工神經網絡預測葉綠素a 濃度取得了較高的預測精度。

（1）本文分析了與葉綠素a 濃度相關要素的長短期依賴關系，發現在不同的時間點，各要素間依據相關系數可以分為兩種依賴關系，從查詢文獻中發現，本文作為第一次提出對于原始要素的分析研究。

（2）本文依據要素間不同的依賴關系所得的分類結果，我們將原始輸入要素分為兩個不同的子網絡進行訓練，不同的子網絡所采用的神經元和激活函數不同，最后在融合層進行特征的融合，該網絡結構具有一定創新性。本文所提出的網絡模型結構與Regression、MLP、RNN 在葉綠素a 濃度的預測結果中，本文的模型誤差均有大幅度的下降（圖8，圖9）。

（3）本文所提出的模型具有收斂速度快，訓練過程平穩的特點。從圖7 中可以發現，本文所提模型結構訓練誤差下降較快，在300 步后，誤差趨于收斂狀態，其次我們發現誤差下降過程平穩，沒有出現劇烈的抖動情況，這一現象說明了模型在收斂速度及訓練過程中的優點，另一方面也證明了本文所提模型的可行性。

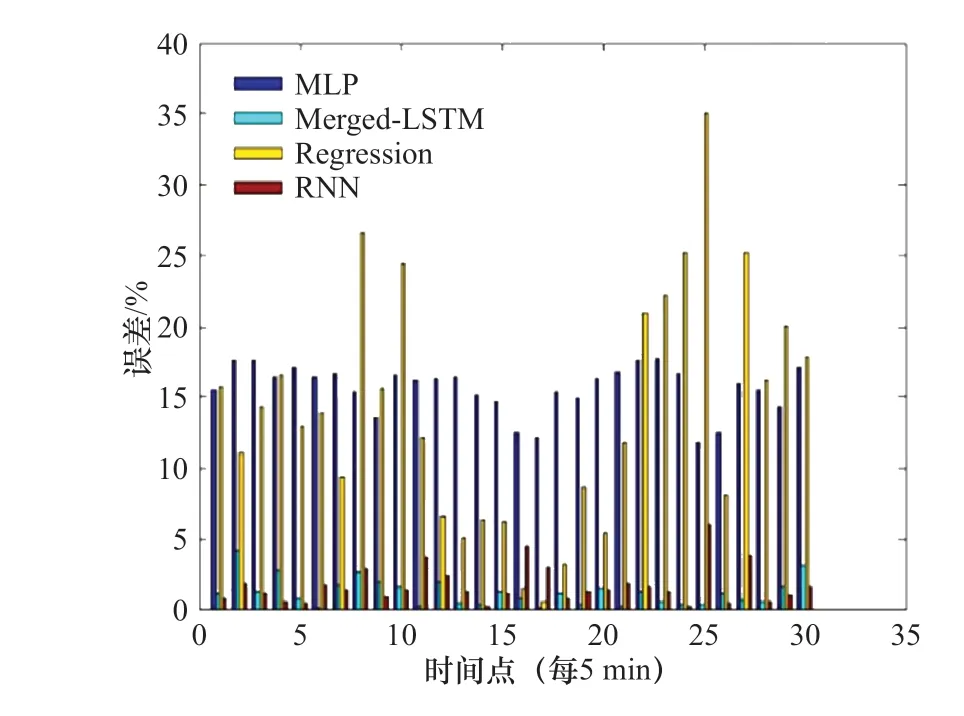
圖 9 實驗結果圖Fig. 9 Experimental results