染缸排產建模及滑動時間窗啟發式調度算法

隗千千，董興業，王煥政

(北京交通大學 計算機與信息技術學院，北京100044)

0 引言

染缸排產是為多染缸、多訂單、分批次的染色任務制定生產計劃的問題，需要考慮生產訂單分配、工藝約束、訂單要求和客戶要求等限制因素，是一個組合優化問題。由于缺乏可用的軟件工具，我國的印染車間制定染缸排產計劃時很大程度上還依賴于計劃人員的經驗。其染色工藝約束復雜，生產任務規模大，給計劃人員帶來了巨大的壓力，排產方案的質量也難以保證。

近年來，許多學者在染缸排產模型及調度算法方面作了許多研究。通常，染缸排產模型主要考慮完成時間、洗缸成本、染缸切換成本等。文獻[1]以最小化染色成本、洗缸成本、庫存成本、延誤代價為優化目標，提出了一種基于啟發式規則的改進極值優化算法用于求解小規模問題；文獻[2]考慮了產品拆分分批，最小化產品延誤代價和切換成本，使用遺傳算法求解；文獻[3]考慮了訂單的拆分和合并分批，以最小化延誤時間和最大化染缸利用率為目標，設計了構造型啟發式方法；文獻[4]以延誤代價和染缸利用率為目標，考慮相容作業組的拼缸、與作業順序相關的設置時間，構建了問題模型并提出了一種多目標人工蜂群算法；文獻[5]針對機器相同的排產調度問題，考慮產品分批、與作業順序相關的設置時間等因素，以最小化完工時間為目標，設計了混合整數線性規劃模型，將產品的調度過程分為批次構建和批次調度兩個子問題，使用多種群遺傳算法求解；文獻[6]在染缸容量上限和下限約束、訂單優先級約束、洗缸約束等約束條件下，使用量子遺傳算法，對訂單進行拆分與合并分批，可完成小規模問題的染缸排產調度。除了針對印染問題的研究，與之最相似的問題是批處理調度問題[7-10]。該類問題應用背景廣泛，包括半導體生產[11]、鋼鐵制造[12]、輪胎制造[13]、印刷線路板生產[14]等。若簡化約束條件，染缸排產調度問題屬于異構并行機、作業大小不同、作業組不相容、設置時間與作業順序相關的批處理調度問題，是NP-難問題。

實際生產中問題的規模往往很大，約束條件和生產限制因素更加復雜，對排產效率要求也比較高。一般情況下，一個染紗車間的月訂單量至少有500個，染缸數量有幾十個，排產調度時需要考慮產品的特殊工藝(如熒光產品)、頭缸生產以及染缸的維護計劃等約束。此外，現有生產計劃對染缸排產還存在一定的限制。相比之下，上述對染缸排產問題的研究中所構建的問題模型未考慮特殊工藝、頭缸生產、染缸維護計劃、進出缸并發約束，也未考慮增量調度，與實際生產條件相差較大，限制了算法的適用性；另外，雖然文獻中批處理調度問題的研究成果較多，但是這些算法不能用于本文所提出的問題模型。綜上所述，染缸排產模型及優化算法在實用性和適用性方面亟待提高。

本文根據印染企業的生產需求，以最小化延誤代價、染缸切換成本、洗缸成本為目標，在已有問題模型的基礎上，考慮產品頭缸、禁熒光、染缸維護、現有生產計劃安排等新的生產約束，建立更符合實際生產條件的染缸排產增量調度模型，并基于啟發式規則設計求解算法，提高排產效率，節約生產成本。

1 染缸排產調度問題模型

1.1 問題描述

染缸排產調度問題是通過對產品進行拆分分批或者合并分批將多個產品安排到多臺染缸中排產，需解決的問題是在不改變原生產計劃中產品批次劃分的情況下，對新增產品進行批次劃分，為各批次安排染缸，確定批次開始加工時間，在滿足各種約束條件的同時使調度目標最優。

印染企業的生產訂單首先由銷售部門下發給計劃部門，然后計劃部門根據實際生產情況制定生產計劃，并傳達給生產車間。每個產品從進入企業資源計劃系統到包裝入庫的處理過程可表示為如圖1所示的頂點活動(Activity On Vertex，AOV)圖。產品調度僅需要確定C4和C5的開始時間；由于排產過程不涉及C0和C6，因此它們可看作虛節點，時長為0天，其他節點的時長與具體產品有關；當產品沒有頭缸時，不需要工序C4。

圖1 生產流程AOV圖Fig. 1 AOV diagram of production process

染缸排產調度問題的約束條件包括以下幾個方面：

1) 染缸容量限制約束。批次加工量必須在所選染缸容量上限和下限之間，相同的容量上限為同一缸型。

2) 染缸維護時間約束。染缸有多個維護時間段，維護期間染缸不可用。

3) 加工時間約束。圖1中各工序在執行前，其前序工序必須完成，否則應延遲排產，延遲時間為其前序工序的最大準備時長。

4) 禁熒光約束。染缸加工熒光產品后需連續加工一定缸數的非熒光產品之后才能加工禁熒光產品。

5) 進出缸并發約束。批次在開始加工前和加工結束后有進缸和出缸操作，同一時刻執行進缸和出缸操作的數量有一個上限，該限制和工人資源量有關。

6) 拼缸約束。幾個產品合并在一個批次加工時，稱為拼缸；拼缸批次的各產品必須來自同一產品組。

7) 拆缸約束。一個產品拆分成幾個小的批次加工以適應染缸容量，稱為拆缸。為了保證大貨產品的生產質量，不同量級的產品的最小拆分閾值不同，拆分的各個批次中，最多有一個批次的生產量小于該拆分閾值，拆缸需盡可能拆分成大的批次；原生產計劃中已經拆缸的批次不允許再次拼缸；頭缸不允許拆缸。

8) 原生產計劃中已經拆缸或者拼缸的產品，再次調度時不再進行批次劃分。

本文首先對數據作了預處理：依次檢查產品的各項工序，計算產品的延遲排產時間，記為產品的釋放時間。例如，某產品的C1、C2、C3工序未完成，則其延遲排產天數為上述三工序的最大準備時長。由加工時間約束可知，產品的最早加工時間應不早于釋放時間。

1.2 模型構建

1.2.1 符號定義

1)集合和索引。

M為染缸集合，索引m；J為產品集合，索引i、j；B為批次集合，索引b、c；Jb為批次b的產品集合，Bj為產品j的批次集合；F為產品分組集合，索引f，Jf為組f的產品集合；FL_J為熒光的產品集合，FL_B為熒光的批次集合，FL0_J為禁熒光的產品集合，FL0_B為禁熒光的批次集合；SP為并發時間段集合，SMm為染缸m的維護時間集合，索引sp。

2)變量。

mb表示批次b使用的染缸，sb為批次b的開始加工時間，eb為批次b的結束加工時間，tb為批次b的染色類型；qjb表示產品j在批次b中的加工數量，hjb表示產品在批次中的生產狀態(若產品j在批次b中為頭缸，則值為1，否則為0)。

Stt′為從染色類型為t到染色類型為t′的洗缸時間；Pju為產品j在缸型為u的染缸的加工時長；ssp為時間段sp的開始時間，esp為時間段sp的結束時間，nsp為時間段sp的進出缸并發數量。

3)參數。

Z表示頭缸未確認時延遲排產時長，U表示批次任務的出缸時長，L表示批次任務的進缸時長，V表示熒光批次和禁熒光批次間隔序列長度，P表示進出缸最大并發數目。

1.2.2 模型表示

在染缸排產建模時，目標函數中主要考慮排產延誤、洗缸成本、染缸切換，而模型實用性主要體現在約束條件中。

用S表示一個可行解，則每個染缸的執行序列為一個部分解，染缸m部分序列可表示為Sm=(b1,b2,…,bk)。同一產品的不同批次之間更換染缸會造成批次的質量差異，產生染缸切換成本，染缸m上的批次序列的染缸切換成本為：

(1)

其中：

(2)

同一染缸的相鄰批次之間需要洗缸，洗缸時間與相鄰批次的染色類型有關，染色類型有白、淺、中、深四種，一般來說，淺色批次到深色批次的洗缸時間小于深色到淺色批次的洗缸時間。Stt′表示加工完染色類型為t的批次后，在加工染色類型為t′的批次之前的洗缸時間。染缸m上的批次序列的洗缸成本為：

(3)

每個產品都有交貨日期，延期交貨會有一定的懲罰，懲罰大小取決于產品的優先級權重和延誤時長，產品j的延誤代價可表示如下：

(4)

其中：

cj=max{eb|b∈Bj}

(5)

目標函數及約束條件如下：

(6)

s.t.

(7)

lap(sp,b)=0； ?m∈M,sp∈SMm,b∈Sm

(8)

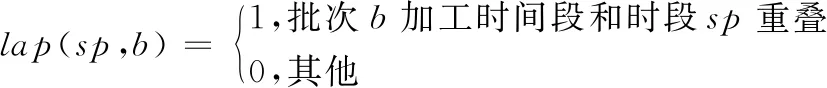
(9)

min {sb}≥rj;?j∈J，b∈Bj

(10)

In(f0(b,Sm),Sm)-In(b,Sm)≥V;

?m∈M,b,b0∈Sm,b∈FL_B

(11)

nsp≤P;?sp∈SP

(12)

fj1=fj2;?b∈B,j1,j2∈Jb

(13)

|MBj|≤1;?j∈J,b∈Bj,MBj={b|qjb≤thj}

(14)

(15)

(16)

qjb,sb,eb∈N

(17)

式(6)定義了調度目標，是染缸切換成本、洗缸成本和延誤代價三項成本的線性和。

式(7)表示染缸容量約束，批次加工量(各產品在該批次中加工量之和)應在染缸容量上限和下限之間；式(8)和式(9)表示染缸維護時間約束，任意批次的加工時間都不與染缸維護時間重疊；式(10)表示加工時間約束，產品的任意批次開始加工時間都晚于釋放時間；式(11)表示禁熒光約束，熒光批次b與其之后的第一個禁熒光批次之間至少間隔V個批次；式(12)表示進出缸并發約束，任意時間段sp執行進出缸操作的數量少于P；式(13)為產品的拼缸約束，批次中加工的產品都屬于同一產品組；式(14)為產品的拆缸約束，產品最多有一個批次加工數量小于拆缸閾值；式(15)為頭缸拆缸約束，若在批次中加工頭缸，則加工量為全部頭缸數量，即頭缸不允許拆分；式(16)為產品加工數量約束，產品總量等于已完成數量與各個批次加工數量之和；式(17)為變量的整數約束，即時間變量、批次數量均為整數。

問題模型中已知染缸數據、產品數據、現有生產計劃、排產參數等數據，求解產品的分批方案和新的排產計劃，其基本問題是并行批處理調度問題，已被證明是一個NP-難問題[15]，因此其衍生問題也是一個NP-難問題，采用傳統的數學規劃方法無法有效求解。染缸排產調度問題約束條件復雜，批次劃分和調度時間都是離散的，時間跨度較長，染缸和產品的數據規模較大，因此依據問題特點和模型約束，設計構造型啟發式方法快速求解是實際生產的迫切要求。

2 染缸排產調度優化算法

為簡化問題，作出如下假設：圖1中工序C1(向客戶確認顏色)、C2(原料備庫)、C3(生產復樣并確定復樣配方卡)的狀態隨調度日期更新，產品的釋放時間也隨之更新；批次一旦開始加工，就不能被中斷；當一個批次加工完成后，就從產品的原計劃生產列表中刪除，不再對下次調度產生影響；由于產品的頭缸不能拆缸，因此假設所有頭缸均存在單獨加工的缸型；缸型相同的染缸，其容量下限也相同；批次加工時間精確到分鐘，釋放日期、交貨日期精確到天。

圖2中所述產品調度算法是根據染缸的可用狀態和當前進出缸并發狀態，計算產品j最佳的分批方案和批次加工時間，基本步驟如下：

圖2 STWS算法流程Fig. 2 Flowchart of STWS algorithm

步驟1 若產品j的原計劃批次集合Bj不為空，則轉至步驟6；否則生成拼缸調度計劃PlanCj(動態拼缸算法)，即拼缸批次bj。

步驟2 若PlanCj不存在，則轉至步驟5；否則若PlanCj加工開始時間在workT內，Planj←PlanCj，算法結束。

步驟3 若|Jbj|>1，則生成|Jbj|≤1的計劃PlanC0j(動態拼缸算法)；否則轉至步驟5。

步驟4 若PlanC0j存在且不會發生延誤，則Planj←PlanCj，算法結束；否則若產品當前加工部分不可拆缸，則算法結束。

步驟5 生成拆缸計劃PlanSj(拆缸算法)，令Planj←PlanSj。

步驟6 調整PlanSj批次，選擇合適的染缸和加工時間(批次最佳排序算法)，優化延誤代價、換缸成本、洗缸成本，算法結束。

在使用動態拼缸算法和基于回溯搜索的拆缸算法對產品進行調度時，需要確定產品的待調度數量和產品的最晚加工完成日期。不同狀態下的產品調度數量不同，主要和頭缸有關，根據約束條件(15)和(16)，可得產品j的待調度數量qj′的計算方法為：

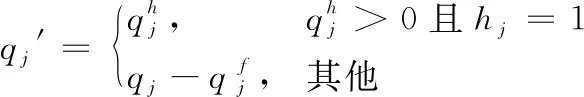
(18)

為降低延誤代價，產品發生延誤時，應該保證延誤最短，因此，在產品調度過程中，初次調度最晚加工完成日期(截止日期)均為交貨期，在不能成功調度時，最晚加工完成日期每次延后一天，進行迭代調度。

2.1 動態拼缸算法

動態拼缸(Dynamic Combination Batch，DCB)算法首先根據當前調度時間workT選擇滿足并發約束(12)的染缸集合。然后在同一最晚加工時間之前，對于集合中的每個染缸上，計算拼缸方案，將該組合問題轉化為一維背包問題，使用動態規劃算法計算產品j的最佳拼缸產品集合，并確定拼缸批次的加工時間，選擇第一個可行的拼缸批次返回。若所有拼缸批次都晚于最晚加工時間，則推遲該時間點，重新查找拼缸方案。最后是優化階段，在可用染缸集合中查找拼缸批次評價指標最小的染缸，確定批次所用染缸及開始加工時間。以下是DCB算法偽代碼描述。

算法1 動態拼缸算法。

輸入：待調度產品j；

輸出：拼缸批次b。

計算產品j的可拼缸產品集合combJ：

combJ={j′|j′∈J,j′∈Jfj,rj′≤workT}

計算產品j和combJ中產品的待調度數量

IF(workM為空) RETURN NULL

初始化最晚加工完成日期combD←dj，拼缸標記combF← false，染缸訪問序號i← 0

WHILE (true)

WHILE (i<|workM|)

計算滿足容量約束(7)的拼缸產品組合combJmi

IF (combJmi為空)i←i+1

ELSE

計算b在mi的加工時間，令combF← true

IF (eb≤combD) BREAK

ELSEi←i+1

END WHILE

IF(combF==false) RETURN NULL

ELSE

IF (eb≤combD) BREAK

ELSE 更新combD←combD+1，i← 0

END WHILE

workM′為workM中滿足批次b容量約束的染缸，計算b在workM′中各個染缸mi的加工時間，得到新的批次bi，則可行批次集合comB={bi|ebi≤combD}

計算bi∈comB所用利用率prbi和洗缸代價csbi，選擇拼缸批次評價指標Cbi最小的批次b；RETURNb

上述染缸利用率和缸批次評價指標的計算方式為：

(19)

Cbi=umi(1-prbi)+csbi

(20)

2.2 拆缸算法

2.2.1 基于回溯搜索的拆缸算法

由于產品拆缸有最小閾值限制，并且產品拆分時盡可能拆分為大的批次，若使用簡單貪心算法直接選擇最大容量的染缸進行拆分，會產生很多拆缸方案不可行的情況，因此本文提出基于回溯搜索的拆缸算法(Batch split Algorithm based on Backtracking Search， BABS)。

BABS是一種隱枚舉算法，計算滿足約束條件最佳拆缸方案，由大到小選擇染缸，在每個染缸上盡可能地續缸生產，直至拆缸不可行，此時刪除當前方案中已安排的最小染缸，回溯查找可用染缸，然后繼續分批，其偽代碼描述如下。

算法2 基于回溯搜索的拆缸算法。

輸入：待調度產品j；

輸出：拆缸方案PlanSj。

計算產品j的待調度數量qj′

獲得可用染缸workM，按缸型降序、可用時間升序排序

初始化最晚加工完成日期splitD←dj

初始化基本變量：可延誤拆缸標記splitF← false，拆分批次集合PlanSj← NULL，所用染缸的可加工最大量uC← 0、最小量lC← 0，染缸訪問序號i← 0

WHILE (true)

從i開始順次查找第一個滿足式(21)或(22)的染缸mi

IF (mi不存在)

WHILE (PlanSj!=NULL)

回溯查找新的可用染缸mi；BREAK

END WHILE

IF (mi不存在)

IF (splitF==true)

//可延期拆缸

splitD←splitD+1，重新初始化基本變量

CONTINUE

ELSE 產品拆缸失敗，算法異常結束

WHILE (true)

IF (mi滿足式(21)或(22))

在染缸mi上生成新的批次b

ELSE BREAK

IF (eb>splitD)

//可通過延期拆缸

更新splitF← true，i←i+1；BREAK

ELSE

lC←lmi+lC，uC←umi+uC

PlanSj←PlanSj∪b

END WHILE

IF (lC≤qj′≤umi) BREAK

END WHILE

調整PlanSj批次的加工數量，使相同缸型的批次加工數量盡可能均勻；RETURNPlanSj

回溯查找染缸的方法：首先刪除PlanSj最后加入的批次newb，然后令i← 0，從i開始順次查找第一個比newb所用缸型小且滿足式(21)或式(22)的染缸mi。

染缸可用條件判斷式：

lmi+lC≤qj′≤umi+uC

(21)

lmi≥thj并且lmi+lC≤qj′

(22)

2.2.2 拆缸優化算法

上述基于回溯搜索的拆缸算法中的基本準則是優先選擇大缸，查找滿足染缸容量約束和產品拆缸約束的拆缸組合方案，這種方式得到的拆缸方案大多使用染缸的缸型種類比較多，一個產品需要在多個染缸上生產，染缸切換成本比較高，產品質量穩定性也變差，因此最佳的拆缸方案是在較大的缸中續缸(而不是選擇最大的染缸和較小的染缸拆缸)。

拆缸優化(Batch Split Optimization，BSO)算法是在基本拆缸方案的基礎上，保證最晚加工完成時間相同、使用拆缸批次數量相同和優先選用大缸的準則，優化洗缸成本和染缸切換成本。每一輪優化都是在同一個最晚加工完成時間前，將生產量均分到較小的染缸中，如果不可行，則保留最大的一個批次，均分剩余加工部分，直到所有批次都被保留或者得到可行方案。以下是算法的偽代碼描述。

算法3 拆缸優化算法。

輸入：基礎拆缸方案PlanSj；

輸出：優化拆缸方案OPlanSj。

根據計算產品j的待調度數量qj′

獲得可用染缸workM，可用缸型typeM，按缸型降序、可用時間升序排序

根據PlanSj計算最晚加工完成日期splitD=max {eb|∈PlanSj}

初始化待拆缸數量n← |PlanSj|，所用染缸的可加工最大量uC← 0、最小量lC← 0；將PlanSj按照缸型從大到小排序

IF (n==1) RETURNPlanSj

WHILE (|PlanSj|>1且n>1)

在typeM中查找n缸可加工qj′的染缸m：

n*lm+lC≤qj′≤n*um+uC

IF (染缸m不存在)

刪除PlanSj中使用染缸缸型最大的批次bmax，

OPlanSj←OPlanSj∪bmax

ELSE

在splitD之前，在所有缸型為um的可用染缸中優先續缸加工n個批次，加入集合OPlanSj中

END WHILE

調整OPlanSj批次的加工數量，使相同缸型的批次加工數量盡可能均勻；

RETURNOPlanSj

2.3 批次最佳排序算法

使用BABS計算產品j的拆缸方案PlanSj(|PlanSj|>1)時，僅考慮交貨日期之前每個染缸上的最大加工能力，優先選擇了開始可用時間最早的染缸。由于染缸有維護計劃，可能發生這種情況：可用時間最早的染缸，其維護時段很長且開始時間很早，進而可用時間段相對其他同缸型的染缸較短，批次選擇染缸數目較多。一方面會增加洗缸成本，另一方面也會增加切換成本，導致產品質量不穩定。

在原生產計劃中已經拆缸或者拼缸的產品，產品的批次劃分已經確定，但是具體的染缸未確定，因此需要確定合適的染缸以及加工時間。

以上兩種場景都需要進行批次調度，本文設計了批次最佳排序(Batch Optimal Sorting，BOS)算法，調整批次在各個染缸上的生產順序，使得產品j的延誤時間最短，染缸切換成本、洗缸成本最小。將產品的各個批次按照缸型分組，對使用同一種染缸缸型的批次，統一在指定缸型的染缸上調度，每一組都搜索一個最長續缸方案。以下是算法步驟描述：

步驟1 設置最佳方案最晚加工完成日期combD為max{eb|b∈PlanSj}。

步驟2 將PlanSj中的批次按照批次所使用缸型降序排序，計算PlanSj使用的所有染缸缸型集合MType，設置MType訪問序號i為0，最佳調整方案為OPlanSj。

步驟3 對染缸進行篩選，獲得指定缸型染缸workM。

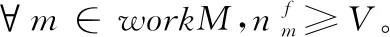
步驟4 若訪問序號i≥|PlanSj|，則批次調整完成，算法結束；否則，獲得PlanSj中使用染缸缸型為tyi的批次Btyi，獲得workM中缸型為tyi的染缸Mtyi。

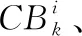
(23)

2.4 進出缸并發控制策略

由于整個調度過程是按照時間先后順序進行的，并發時間段的占用不可逆，調度時每個批次可用時間段僅和當前并發狀態和染缸狀態相關。

上述DCB算法、BABS、BSO算法和BOS算法在查找批次在染缸上的可用時間段時，需要嚴格滿足染缸的維護時間約束和并發時間段約束(進出缸時間段同時滿足并發約束)；產品生成可行計劃后，按照批次的時間先后順序，依次分配到指定染缸上，每分配一個批次，都重新劃分時間段，更新集合SP以及各時間段的并發數量nsp。

3 實驗評測

本章首先給出了實驗所用的參數和數據集，然后將STWS算法與人工排產方案進行對比，最后對算法的增量調度進行評測。

本文所使用的產品和染缸數據均從真實數據集中隨機抽取，調度日期為2018年4月1日，染色類型均勻分布。

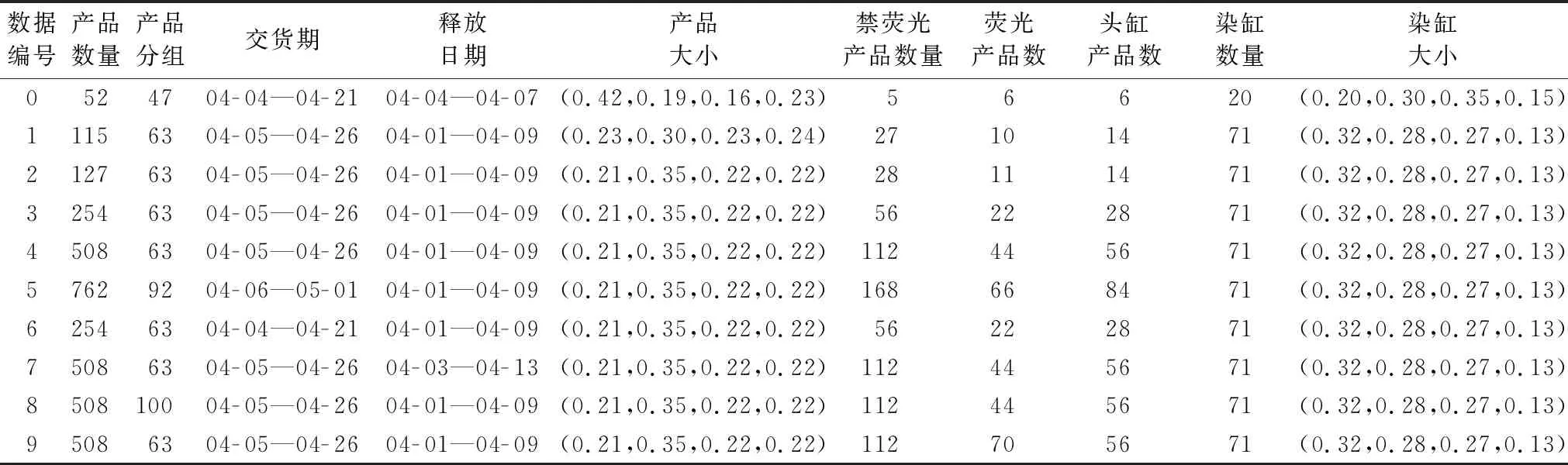
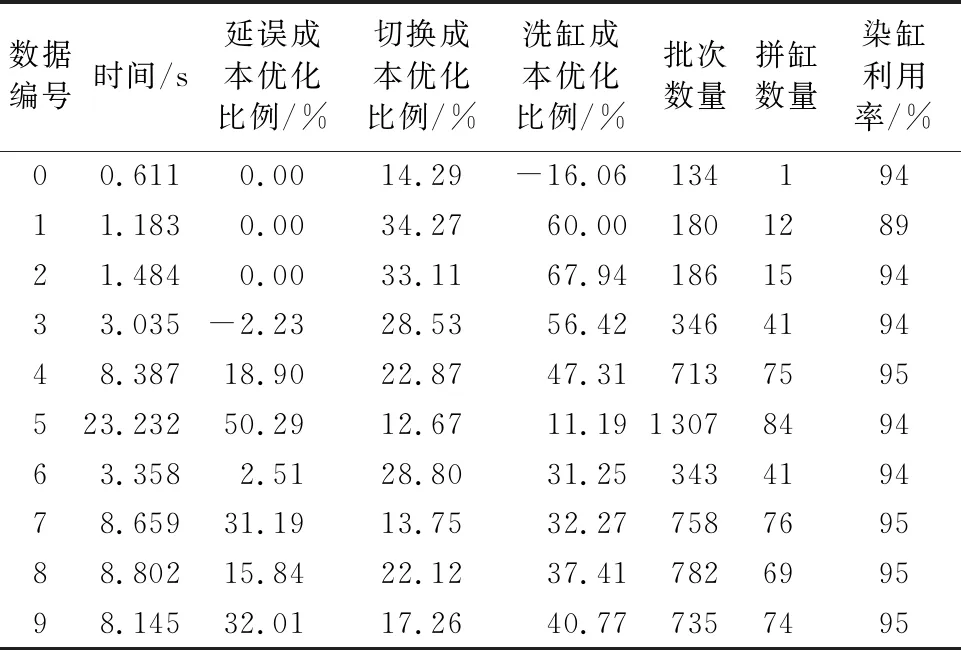
根據產品生產量將產品分為4類：小(1≤qj≤100)、中(100

表1列出了算法需要的參數取值列表。

表2列出了實驗中使用的測試數據集，其初始調度計劃均為空。其中第6組數據是第3組數據的各個產品的交貨期整體提前1～5天所得，其他數據與3號相同，第7、8、9組數據是對第4組數據部分處理得到的：第7組數據延遲了產品的釋放日期；第8組數據減小了可拼缸數目，即在產品數量相同的情況下增加了分組數目；第9組數據增加了熒光產品所占比例。

表1 參數取值列表 Tab. 1 List of parameter values

表2 實驗中使用的數據集 Tab. 2 Dataset used in the experiment

人工排缸方案一般是由經驗豐富的計劃員完成，約束執行往往不是很嚴格，當實際排產發生約束沖突時，只能通過延遲染缸的后續批次或者取消某些批次來緩解，使得排產不能按照原計劃實施。這里使用普通規則(General Rule，GR)算法來模擬人工排缸過程，并與STWS算法對比。與STWS類似，GR算法是按照產品的優先級順序(交貨日期升序、產品優先級權重降序、釋放日期升序排序)，依次對產品進行調度；但是GR算法在產品調度時沒有使用最優調度策略，而是使用貪心方法對產品進行拆缸和拼缸；批次調度時，選擇洗缸時間最短的染缸依次調度，不再進行迭代優化。表3為GR算法的調度結果。

表3 GR算法調度結果 Tab. 3 Scheduling results using GR algorithm

使用STWS進行調度，可得到如表4所示的調度結果，其中，延誤成本優化比例=(GR算法延誤成-STWS算法延誤成本)/GR算法延誤成本，同理可得切換成本優化比例、洗缸成本優化比例。從調度結果可以看到，在數據規模適中(產品數量在100到500左右)的情況下，該算法可在10 s內給出可行方案。相對于GR算法，STWS算法的染缸切換成本、洗缸成本明顯減小，批次數量有所減少、拼缸批次有所增加，染缸利用率明顯提高，以上結果說明動態拼缸算法和拆缸算法有利于更好地利用染缸的生產能力；在延誤代價方面，當數據規模較大時，STWS算法優化效果顯著，最高可優化50%以上，數據規模較小時，優化不明顯，這是因為產品數據較少時，可優化空間也有限；除第0組數據外，洗缸成本均有大幅度降低，說明批次最佳排序算法能有效安排同一產品的不同批次進行續缸生產，從而節約了洗缸成本；對于第0組數據，洗缸成本上升的主要原因是批次調度時為增加續缸而選擇了首次洗缸成本較高的染缸。綜合以上幾個方面，STWS算法性能優于GR算法。

表4 STWS算法相比GR算法的優化結果 Tab. 4 Optimization results of STWS algorithm compared to GR algorithm

從表4的第4、7、8、9組數據的調度結果可以看到，在數據規模適中時，無論什么特點的數據，STWS算法性能都比較穩定，延誤代價優化程度穩定在20%～30%，切換成本優化程度在10%～20%，洗缸成本優化程度在30%～50%，總體優化效果都較為明顯。

第4組數據的產品數據是在第3組數據的產品數據的基礎上加入了一些新的產品得到的，因此將第3組數據的調度計劃作為第4組數據初始計劃用于增量調度測試，表5為增量調度結果。相對于第4組數據的無初始調度計劃的調度結果，增量調度的消耗時間短，這是由于增量調度時調度計劃中已經分批的產品不再經過分批過程，從而節約了調度時間。不過，由于已調度過的產品的批次劃分不能改變，減小了優化空間，因此各項成本值均有所增加，拼缸批次數量減少，染缸利用率有所降低。

表5 STWS算法在第4組數據上的增量調度比較 Tab. 5 Incremental scheduling of STWS algorithm on the 4th data

4 結語

根據印染車間的生產需求，考慮產品的多樣化、異構并行機、批次劃分約束、頭缸約束、禁熒光約束、染缸維護計劃等實際場景，建立了染缸排產增量調度模型。本文提出了構造型啟發式算法——滑動時間窗調度(STWS)算法，按照一定的規則和邏輯對產品進行調度，最小化延誤代價、洗缸成本、染缸切換成本。產品調度過程中，設計了動態拼缸(DCB)算法和拆缸算法(BABS、BSO)進行批次劃分，使用批次最佳排序算法調度批次。通過實驗對比，檢驗了STWS算法增量調度的性能，在數據規模適中時，STWS算法能夠在10 s內給出可行方案，相比人工排產方案，該算法顯著地降低了生產成本和延誤代價，目前已在某企業的生產系統中上線運營。

由于算法大多數場景都是增量調度模式，批次劃分僅限于第一次調度的產品，批次劃分確定后，批次的調度是影響生產代價的重要因素，因此批次調度的全局優化是接下來的研究重點。