LMS算法自適應均衡器的設計

周 超

（華南理工大學廣州學院，廣東 510800）

均衡技術是通信領域三大技術之一，時域均衡具有很強的實時性，被廣泛使用。通過軟件或數字芯片，可以實現數字濾波器的設計，而不必依賴電感、電容等模擬元件。本研究通過系統建模、仿真的方式完成了均衡內部參數的設計。在參數選取上克服了隨意性并節省了系統資源，對均衡的開發具有一定的參考意義。

1 均衡模型

LMS算法使用最小均方誤差準則，并采用最速下降梯度算法[3]。LMS算法可以概括為兩個過程：濾波和參數調整。第一步初始化濾波器抽頭系數矢量；然后求解當n=n+1時濾波器的輸出；最后求出誤差值并調整抽頭系數值[3]。具體公式為：

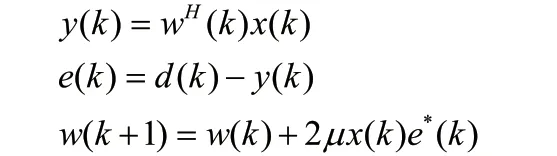
因此，均衡效果的優劣受到信號期望值d（k）、濾波器抽頭更新步長μ、抽頭數量的影響。判決反饋盲均衡器的期望值e（k）由接收信號的判決值替代，因為接收信號本身含有發送信號的信息[3]。

2 LMS判決反饋盲均衡算法仿真

圖1是通信系統使用LMS判決反饋盲均衡與未使用均衡時的效果對比。從圖1的a、b中顯示出使用均衡后，原本混疊的碼元顯著地分開了。圖1中c的誤碼率數據表明，使用均衡后的通信質量明顯提高。

圖1 LMS判決反饋盲均衡使用前后效果對比

為了更清晰地觀察該均衡方案的校正效果，因此在同等條件下將信道誤碼率提高到 進行仿真，其中誤碼率統計部分每一百個碼元顯示一個點，圖2為仿真結果。

據圖2可知，在信道誤碼率是7.4204*10-3時，LMS判決反饋盲均衡器仍然能通過少量碼元就調整好參數，進而適應信道特性，降低系統的誤碼率。因此，在該環境下LMS判決反饋盲均衡是一種有效的方法。

圖3為LMS判決反饋盲均衡器在信道誤碼率分別為7.4204*10-3和3.7201*10-3環境下、抽頭更新步長μ分別為1/32、1/64、1/128時的誤碼曲線。據圖可知，在步長μ取不同值時，系統穩定后的余差相近。因而主要從系統收斂速度、工程實現難易、資源占用大小三個角度進行考慮（相較于除法運算，FPGA更適合移位操作，因此更新步長選取2n值），所以選用1/32作為抽頭系數更新步長值。

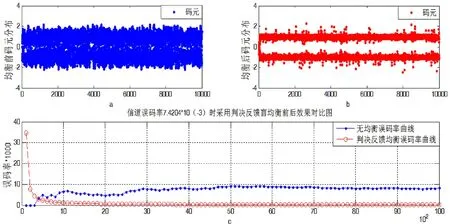
圖2 LMS判決反饋盲均衡前后效果對比

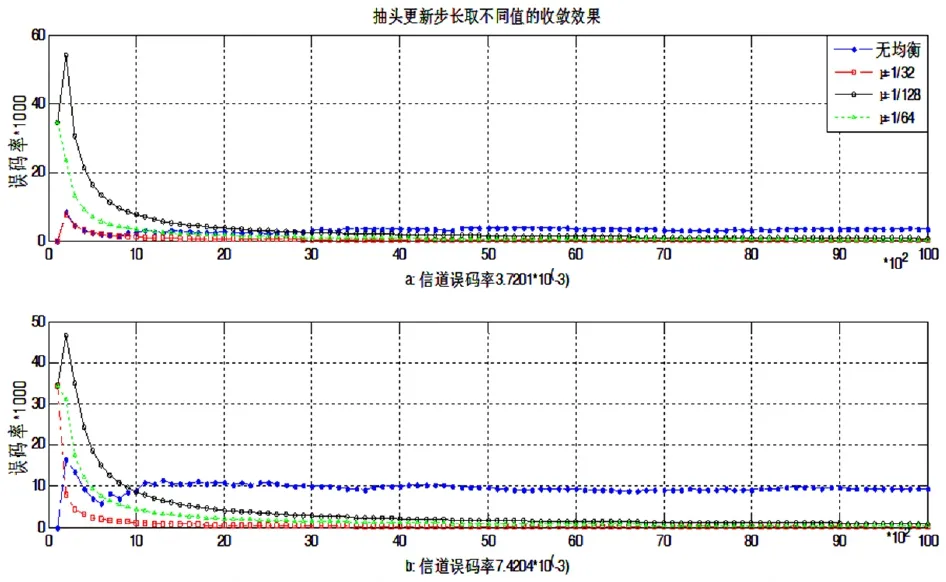
圖3 更新步長仿真結果

若更新步長一定，即使將均衡濾波器長度不斷加長，結果也不會有大的改變。圖4為在更新步長μ取1/32時，抽頭個數分別取5、7、9、11時的誤碼率仿真結果。由圖可知，抽頭個數分別為5、7、9、11的均衡器均能快速收斂，此時從資源占用、收斂后的誤碼率方面考慮，采用5級抽頭的濾波器。

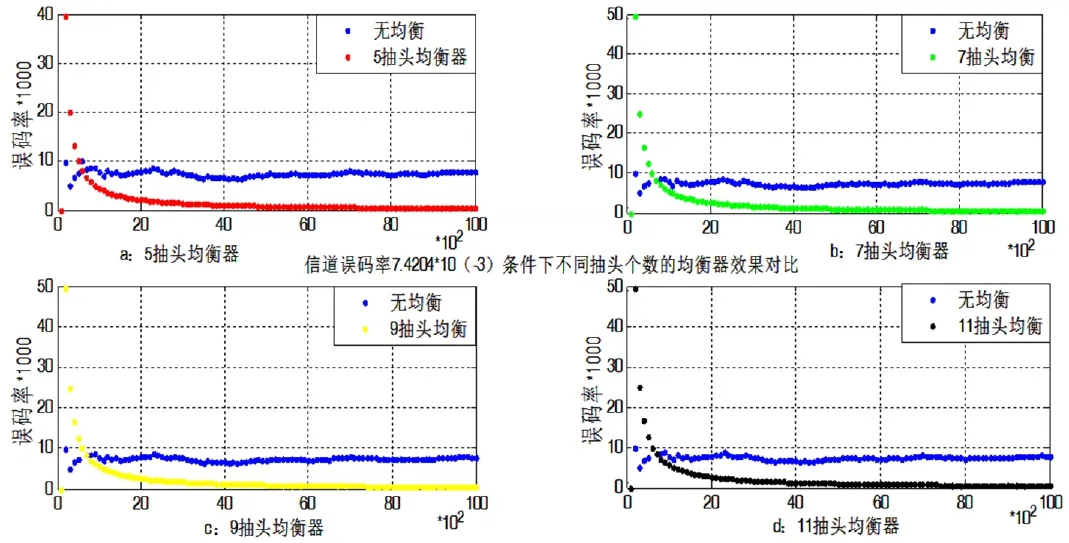
圖4 不同抽頭個數LMS判決反饋均衡仿真結果

通過仿真結果可以得到均衡的設計參數，圖5給出了均衡器的內部組成框圖，信號在4級延時后得到第一個輸出。

圖5 均衡器內部組成框圖

3 結束語

本文首先驗證了LMS算法判決反饋盲均衡在高碼率環境下的均衡效果；進而通過MATLAB仿真確定了均衡器的濾波器級數、抽頭更新步長值等均衡器內部設計參數；采用本文能夠有效的實現基于LMS算法的自適應數字均衡器的設計。