低復雜度頻域迭代均衡技術

王曉春，陳佳怡，董 超

(1.中國電子科技集團公司第五十四研究所，河北 石家莊 050081；2.陸軍邊海防學院，新疆 烏魯木齊 830001；3.北京郵電大學，北京 100786)

0 引言

迭代均衡最早是受迭代信道譯碼思想產生的。隨著Turbo碼[1-2]的引入，信道譯碼器能夠輸出似然比軟信息，該信道能夠反映信道譯碼結果的可靠度。通過將信道譯碼軟信息反饋到前端均衡器，均衡器的系數能夠根據信道反饋的可靠性進行優化。根據信道譯碼的可靠性，在每次迭代處理過程中，前端均衡器的系數需要進行更新。隨著迭代的進行，均衡器和譯碼器的性能最終收斂。該方法可以用于無線傳輸的多徑信道中，該信道中存在的多徑效應引入的符號間干擾，能夠通過信道反饋輔助下的均衡加以消除[3-5]。在迭代均衡處理中，是以數據塊為單位進行處理，每個數據塊之前添加前綴，前綴的長度需要大于最大多徑時延。通過引入前綴，使得每個數據塊之間沒有相互干擾，從而使得均衡處理能夠在數據塊之間獨立進行。同時由于前綴的存在，使得信號均衡能夠在頻域進行，通過頻域的等效處理，能夠有效降低計算復雜度。

1 信號模型

本文的迭代均衡都是以數據塊為處理單位進行，并需要用到頻域計算，在均衡處理的過程中，需要用到快速傅里葉變換(FFT)。近年來，隨著數字信號處理技術的發展和器件處理能力的提高，FFT往往能夠通過數字處理芯片上的專用IP核實現。針對時域數據塊，能夠通過FFT變換，將其變換到頻域，然后在頻域進行相應的信號處理。根據前綴形式不同，數據塊主要有循環前綴和導頻前綴2種形式。

具有循環前綴的數據塊結構如圖1所示。

圖1 具有循環前綴的數據塊結構
Fig.1 The data block structure with cyclic prefix

如圖1所示，在具有循環前綴的數據塊中，數據長度等于N，該長度也是FFT的點數；數據塊末尾L個數據符號，被復制到該數據塊的起始位置，被稱為循環前綴。循環前綴的長度L需要大于無線信道的最大多徑時延。由于循環前綴的存在，對于一個數據塊的數據來說，能夠通過FFT，進行具有低復雜度特征的頻域均衡。

具有導頻前綴的數據塊結構如圖2所示。

圖2 具有導頻前綴的數據塊結構
Fig.2 The data block structure with pilot prefix

從圖2可以看出，每個數據塊中數據的長度是M，導頻長度為L，M+L之和N等于FFT的點數，導頻的長度L需要大于無線信道的最大多徑時延。對于相鄰的數據塊，采用的導頻樣式也是相同的。基于以上設置，對于總長為N的數據塊來說，也能夠通過FFT，進行低復雜度頻域均衡。在實際的4G LTE和5G NR系統中，傳輸數據塊采用的都是循環前綴的方式，因此以下的數學模型主要針對循環前綴的數據塊展開。

假設FFT的點數為N，則針對循環前綴的數據塊，其信號模型可以統一寫為：

y=Hx+n，

(1)

式中，y∈N×1表示N維的接收信號；向量x∈N×1表示N維的發送信號向量；n∈N×1表示N維的噪聲向量，其服從復高斯分布(0,n0IN)。由于循環前綴的存在，H∈N×N具有循環平移的形式，即H的每一行(列)都可以通過第一行(列)做循環平移獲得，其具體表達式為：

(2)

式中，L表示時域上多徑時延的長度。根據H的循環平移特性，其頻域信道響應矩陣具有對角化特性

G=FHFH=diag{g0,g1,…,gN-1}。

(3)

對角線元素gk,0≤k≤N-1表示在第k個子載波上的信道響應，它的表達式為：

(4)

2 頻域迭代均衡

迭代均衡算法可以在頻域實現[6]。在迭代均衡當中，需要用到信道譯碼器反饋的外信息。根據前一節的定義，對于發送符號向量x中的第i個元素，表示為xi，0≤i≤N-1，還假設發送符號采用QPSK調制。因此，xi可以表示為：

(5)

式中，bi,1，bi,2分別表示xi在實部和虛部各自承載的比特。假設信道譯碼器反饋的外信息用似然比形式表示，則對應bi,1，bi,2的外信息似然比分別表示為lbi,1，lbi,2。在迭代均衡過程中，需要用到譯碼反饋以均衡和方差的形式進行表征。根據似然比，比特均衡和方差的計算公式為：

(6)

(7)

進一步，對應調制符號xi的均值和方差分別表示為：

(8)

vxi=0.5vbi,1+0.5vbi,2,0≤i≤N-1。

(9)

在后續的頻域均衡中，需要用到式(8)和式(9)提供的均值和方差的信息。

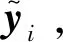
(10)

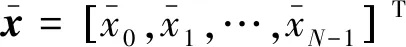
(11)

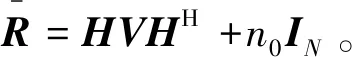
(12)

根據矩陣求逆公式，式(12)可以表示為：

(13)

通過收集所有的xi，均衡結果可以寫成向量的形式：

(14)

式中，矩陣Λ是對角矩陣，其表達式為：

(15)

后續希望能夠通過頻域處理降低式(14)中均衡計算的復雜度。首先引入：

(16)

(17)

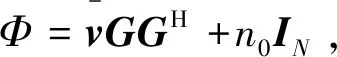
進一步，式(15)中包含的矩陣乘法也可以寫成頻域等價形式：

(18)

根據時—頻域變換的形式，式(18)中計算得到的矩陣其對角線元素相同，因此式(15)可以進一步表示為：

(19)

因此，式(14)的均衡能夠在頻域實現，其頻域處理的表達式為：

(20)

正是基于以上頻域對角化特性，對于接收信號的均衡能夠在頻域實現，此時頻域均衡的復雜度是O(NlogN)的，該復雜度同信道多徑時延的長度無關。

3 仿真結果

Proakis C信道迭代均衡仿真結果如圖3所示。

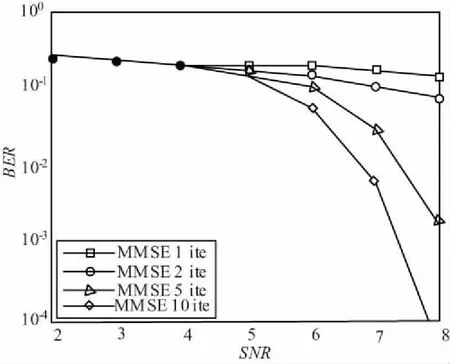
圖3 Proakis C信道迭代均衡仿真結果Fig.3 The iterative equalization performance in proakis C channel

基于以上均衡算法進行了性能仿真。多徑信道模型采用Proakis C信道，多項式為[13,15]8，碼率為0.5，采用QPSK調制，數據塊的長度N=1 024。

從圖3的仿真結果可以看出，經過MMSE迭代均衡10次之后，接收端誤比特率能夠獲得比較明顯的性能增益。

4 最新進展

前述的MMSE均衡方法在多徑衰落信道中具有較強的適用性，但是當信道多徑干擾較為嚴重時，迭代收斂的速度較慢。為了能夠有效加快收斂，文獻[7]進一步引入了序列信息可靠度作為優化指標，通過Cholesky分解，實現信道譯碼軟反饋下的序列符號檢測。進一步，文獻[8]通過引入雙向判決反饋均衡，考慮判決反饋的可靠性，實現嚴重符號間干擾信道中的性能優化。

近年來，基于因子圖的消息傳遞算法[9]被引入到符號間干擾信道的均衡中，尤其是Approximate Message Passing (AMP)算法[10]，Generalized Approximate Message Passing (GAMP)算法[11-12]，通過有效的數學近似，降低了復雜度，同時優化了檢測性能。文獻[13]表明，將GAMP算法用于循環前綴的數據塊均衡，并與信道譯碼構成迭代接收機結構，其迭代收斂性和檢測性能要優于文獻[6]中的算法，并且該均衡算法能夠在頻域實現。

除此之外，基于期望傳播(Expectation Propagation，EP)的檢測算法，也能夠被用于符號間干擾信道的均衡中。文獻[14]將EP形式的均衡器加入到迭代接收機結構中，該均衡器是在時域實現的；文獻[15]采用了EP形式的判決反饋均衡器；文獻[16]中的EP均衡器具有時域抽頭延時線的結構；文獻[17]提出的EP均衡器能夠在頻域實現，降低了均衡復雜度。

5 結束語

迭代均衡是隨著Turbo碼的出現而產生的，其主要設計思想是將信道譯碼軟信息輸出，反饋到前端的均衡器，用于重構干擾分量，從而消除多徑、多天線、多用戶傳輸帶來的干擾，提高接收機的可靠性。隨著Turbo碼、LDPC碼技術的不斷發展，信道譯碼能夠提供的軟反饋信息的可靠性不斷得到改善，同時前端的均衡器結合頻域均衡、判決反饋均衡等技術也在不斷向前發展。隨著基礎信號處理器件和芯片計算能力的不斷提高，迭代均衡已經成為提升接收機性能的一條重要技術途徑，并在實用化系統中得到了廣泛應用。