基于神經網絡和DP算法的PHEV能量管理策略研究

李開放　田一鳴

摘 要：以某款PHEV為研究對象，利用DP算法求得UDDS工況下離線最優控制序列。利用神經網絡對離線最優控制序列及對應汽車狀態進行學習訓練，建立控制變量神經網絡在線預測模型。仿真結果表明，所設計策略實現了離線最優控制變量的良好跟隨，且燃油經濟性提升明顯。

關鍵詞：PHEV 能量管理策略 DP算法 神經網絡

Research on PHEV Energy Management Strategy Based on Neural Network and DP Algorithm

Li Kaifang Tian Yiming

Abstract：Taking a PHEV as the research object， the DP algorithm is used to obtain the offline optimal control sequence under UDDS conditions. The article uses the neural network to learn and train the offline optimal control sequence and the corresponding car state， and establish an online prediction model of the control variable neural network. The simulation results show that the designed strategy achieves a good follow-up of the offline optimal control variables， and fuel economy is significantly improved.

Key words：PHEV， energy management strategy， DP algorithm， neural network

1 引言

能量管理策略是PHEV核心技術之一[1]，其本質是基于工況，發動機和電機的功率分配問題，以期獲得最佳的整車燃油經濟性。與其他策略相比，全局最優策略能獲得理論上最小的燃油消耗值[2]，但其必須在工況已知的情況下，預先求出電機轉矩或發動機轉矩的最優控制序列，然后在仿真或實際實驗中，嚴格對照時間步長，一一離線調用上述最優序列。本文首先利用動態規劃（DP）算法求得PHEV在UDDS工況下的離線最優電機轉矩和傳動比序列，該序列與當前所對應的汽車狀態構成離線數據庫，然后基于BP神經網絡，對該數據庫進行學習訓練，建立控制變量在線預測模型，該模型實現了離線最優控制序列的在線應用，而不需要依照仿真步長，嚴格一一對應調用離線最優控制序列，為后續進一步PHEV基于不同工況的在線能量管理策略研究提供一定理論依據。

2 基于DP算法的離線最優控制序列獲取

DP算法又稱為Bellman優化算法[3]，該算法通過將某個復雜系統求解問題拆分成若干相互關聯子問題，從而將整體求解步驟化，通過局部求解逆推獲得全局最優解。本文所研究PHEV是一款雙軸并聯式混合動力汽車，具有發動機和電機兩套動力源。動力系統需求功率與發動機功率和電機功率關系如公式（1）所示。

Preq（t）=Pe（t）+Pm（t）? ? ? ? ? ? ? ? （1）

式中：Preq（t）為每一時刻車輪需求功率;Pe（t）為發動機功率，Pm（t）為電機功率。

在整車參數及動力系統結構已知，汽車行駛工況確定的前提下，決定動力系統總需求轉矩的只有傳動比。且根據公式（1）可知，電機轉矩和發動機轉矩二者在一個確定的前提下另一個自然確定。因此，本文選擇傳動比和電機轉矩作為DP算法中的控制變量。狀態變量反應汽車當前的一種狀態，本文選擇選擇蓄電池荷電狀態（SOC）以及傳動比作為狀態變量。

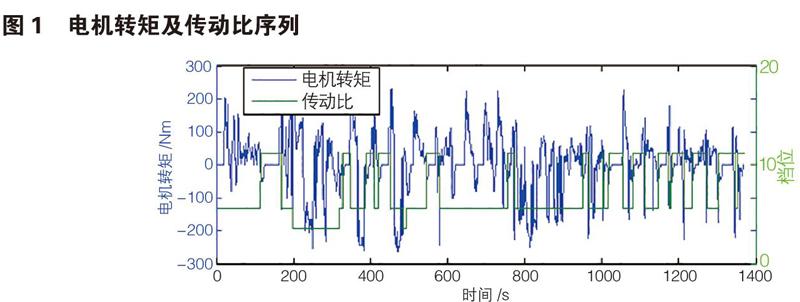
本文主要研究PHEV的燃油經濟性，不涉及排放問題，因此以全局燃油消耗作為最終的目標函數。基于上述原理，編寫DP算法程序，以UDDS工況作為實驗工況，求得該工況下電機轉矩和傳動比序列如圖1所示。

3 基于神經網絡的控制變量在線預測模型設計

3.1 神經網絡基本原理

神經網絡又稱人工神經網絡，由大量神經元（節點）通過一定的連接方式構成，是一種模仿人腦處理信息方式的復雜數學模型，具有學習、記憶和智能處理計算的功能[4]。由于神經網絡具有優越的數據處理分析能力，目前已經成為了許多專業領域一種必不可少的分析工具。根據神經元連接方式不同，神經網絡可分為多種結構。其中BP神經網絡是應用較為普遍的一種網絡。BP神經網絡自學習和自適應性能好，并且還具備良好的魯棒性和泛化能力，理論成熟，因此本文采用BP神經網絡對上述所獲得的離線最優控制變量序列及對應的汽車狀態進行學習訓練，設計控制變量在線預測模型。

3.2 在線預測神經網絡模型設計

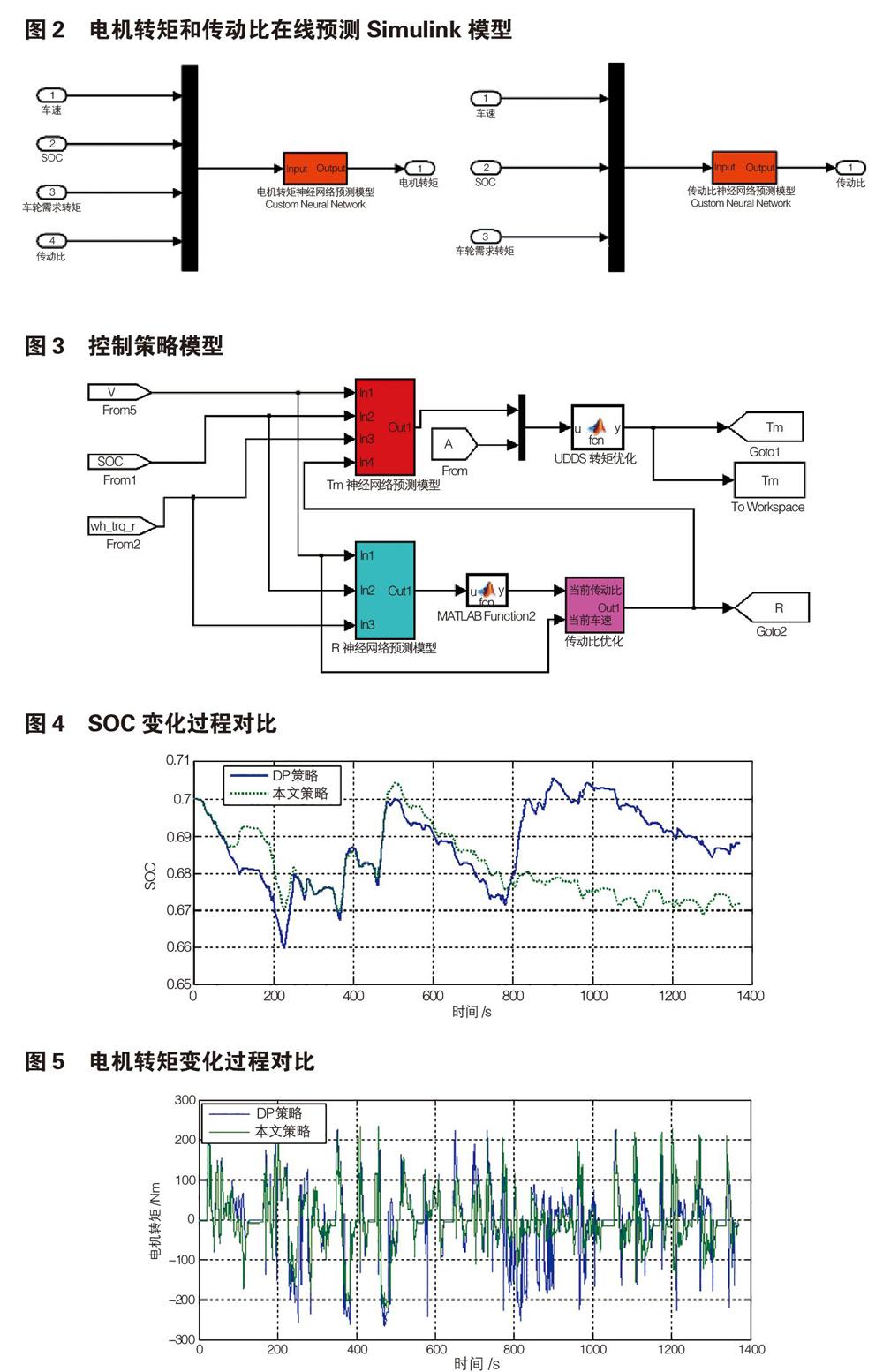
對于單隱含層BP神經網絡，在數據庫樣本個數確定的前提下，為保證網絡訓練的精度，還應確定合適的神經元節點數。本文研究中，通過試湊法，分別以最高網絡回歸值和訓練準確率為目標來獲得最佳的神經元節點數。通過試驗，電機轉矩網絡預測模型選擇節點數為12，其模型的回歸值為0.96;傳動比網絡預測模型選擇節點數為15;其模型的訓練精度為97%，學習訓練結果較為合理。在此基礎上，建立電機轉矩和傳動比神經網絡在線預測Simulink模型，如圖2所示。

4 策略仿真及結果分析

本文所建立控制策略模型核心部分如圖3所示，將圖3所搭建模型嵌入到整車模型之中，使用UDDS工況進行仿真驗證。基于DP算法的離線最優能量管理策略和本文所搭建策略下SOC變化過程對比;圖4為兩種策略下電機轉矩變化過程對比。

由圖4可知，在本文設計策略下，SOC變化范圍為0.661至0.706，范圍波動較小。且SOC變化軌跡與DP策略下軌跡大致相同。圖5電機轉矩值進一步驗證了圖中10中SOC變化過程，且本文策略下電機轉矩變化過程與DP策略下也大致相同。綜上所述，表明所設計的控制變量神經網絡預測模型性能良好，實現了對離線最優序列的良好跟隨。將SOC末值修正至同一水平后燃油消耗對比可知[5]，本文所設計策略燃油消耗為9.18 L/100km，相比于離線最優策略的7.30 L/100km，燃油消耗有一定幅度提升，但相比于默認的電機助力控制策略的11.51 L/100km，其燃油消耗仍然節約了14.8%，燃油經濟性提升明顯。

5 結束語

本文針對某款PHEV，基于DP算法和神經網絡建立一種能量管理策略，實現了離線最優控制序列的在線應用，SOC離線最優軌跡的良好跟隨，且整車燃油經濟性提升明顯，為后續進一步的研究提供了依據。

參考文獻：

[1]秦大同，趙新慶，蘇嶺，楊官龍.插電式混合動力汽車變參數能量管理策略[J].中國公路學報，2015，28（02）：112-118.

[2]蘇嶺，曾育平，秦大同.插電式混合動力汽車能量管理策略研究現狀和發展趨勢[J].重慶大學學報，2017，40（02）：10-15.

[3]勾華棟. 基于動態規劃的并聯混合動力客車能量管理策略研究[D].吉林大學，2015.

[4] 李友坤. BP神經網絡的研究分析及改進應用[D].安徽理工大學，2012.

[5]趙春陽. 基于行駛工況辨識的混合動力客車控制策略研究[D].吉林大學，2015.