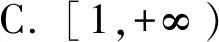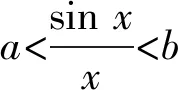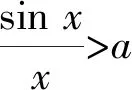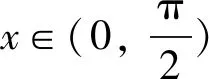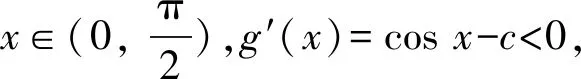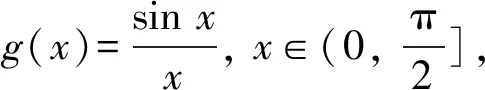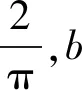當導數遇上三角
林國紅
函數與導數問題是高考壓軸題的常客,也是整套試題中的重頭戲,是最具區分度的亮麗風景所在.隨著高考命題的深入開展,導數壓軸題的命制并沒有走入桎梏,反而涌現出越來越多的典型、新穎的考題.
2019年全國卷Ⅰ文科和理科的函數與導數問題是與三角函數交會的題型,引起師生的較大反響,這類試題可謂多姿多彩,也常考常新.由于三角函數有其獨特的性質,且表達式中含有三角函數無論怎么求導,都會出現含三角函數,從而使問題的后續求解較為困難.因此,如何破解這類函數與導數問題是教師和學生面臨的一大難題.本文筆者以近年高考或模擬考試中與三角函數有關的試題為例,進行分類解答,供讀者參考,希望能拋磚引玉,提高讀者復習效率.
1 函數的極值點與零點問題

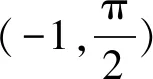
(2)f(x)有且僅有2個零點.

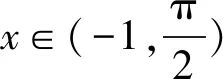
(2)易知f(x)的定義域為(-1,+∞).
① 當x∈(-1,0]時,由(1)知,f′(x)在(-1,0)單調遞增,而f′(0)=0,所以當x∈(-1,0)時,f′(x)<0,故f(x)在(-1,0)單調遞減,又f(0)=0,從而x=0是f(x)在(-1,0]的唯一零點.
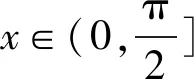
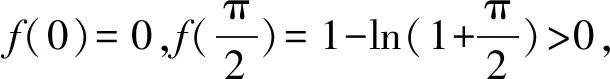

④ 當x∈(π,+∞)時,ln (x+1)>1,所以f(x)<0,從而f(x)在(π,+∞)沒有零點.
綜上,f(x)有且僅有2個零點.

(1)證明:f′(x)在區間(0,π)存在唯一零點;
(2)若x∈[0,π]時,f(x)≥ax,求a的取值范圍.

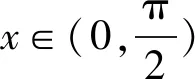
(2)由題設知f(π)≥aπ,f(π)=0,可得a≤0.由(1)知,f′(x)在(0,π)只有一個零點,設為x0,且當x∈(0,x0)時,f′(x)>0;當x∈(x0,π)時,f′(x)<0,所以f(x)在(0,x0)單調遞增,在(x0,π)單調遞減.
又f(0)=0,f(π)=0,所以當x∈[0,π]時,f(x)≥0.又當a≤0,x∈[0,π]時,ax≤0,故f(x)≥ax.因此,a的取值范圍是(-∞,0].

2)要求證一個函數有且只有一個零點,可先用函數零點的存在性定理證明函數存在零點,再證明函數為單調函數.求證函數零點的唯一性,其依據是如果函數f(x)在區間[a,b]上是單調函數,并且f(a)·f(b)<0,則函數f(x)在區間(a,b)上至多有一個零點.如果要證明函數有多個零點,一般要將區間進行分類討論.此類題型考查導數的綜合應用,涉及函數的單調性、函數的零點等多個知識點,綜合考查函數與方程、轉化與化歸、分類討論等思想.
2 函數的極值與最值問題

(1)求曲線y=f(x)在點(0,f(0))處的切線方程;
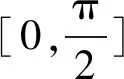

(2)設h(x)=f′(x)=ex(cosx-sinx)-1,則
h′(x)=ex(cosx-sinx-sinx-cosx)=-2exsinx.
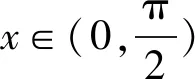
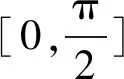

(1)若a≤1,證明:f(x)是定義域上的增函數;
(2)是否存在a,使得f(x)在x=0處取得極小值?說明理由.

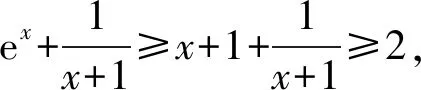
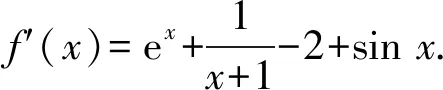


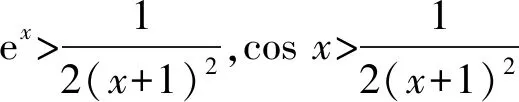
因此,存在a=2,使得f(x)在x=0處取得極小值f(0)=0.

3 證明函數不等式

(1)若函數f(x)存在極小值點,求m的取值范圍;
(2)證明:f(x+m) (2)當m≤0時,有f(x+m)=xln (x+m)≤xlnx,若xlnx ① 若x∈(0,1],則ex+cosx-1>0,xlnx≤0,所以xlnx 綜上,f(x+m) (1)若x=x0時,f(x)取得極小值f(x0),求實數a及f(x0)的取值范圍; (2)當a=π,0 s(x)>s(π)=1+mln π>1. (1)求證:f(x)≤0; 由上述例子可看出,導數與三角函數交會的問題題型眾多,函數的表達式多是三角函數與ex,lnx相結合,主要考查函數的單調性、零點、極值與最值、恒成立等問題.由于三角函數的特殊性,所以試題不僅考查導數公式和導數的運算法則,還考查三角函數中的恒等變換(倍角公式,化一公式等)、周期性、有界性、常見的三角不等式等.思想方面主要考查轉化與化歸、方程與函數、數形結合、以直代曲等.總之,這類問題綜合考查考生邏輯思維、轉化、推理與運算等能力,綜合度較高,對于考生運用所學知識,尋找合理的解題策略以及推理論證能力有較高的要求. 因此,在復習備考中要注重突出主干知識,導數試題注重對導數的幾何意義、運算法則、導數在研究函數中的應用等方面進行考查.函數單調性是核心,要深化對函數單調性的認識,復習時需注重導數法在函數單調性中的應用.同時,還需注重變式訓練,注意揭示解題規律,歸納提煉方法,即復習時要善于總結,將涉及三角函數的導數試題分類探究,并歸納出常用的解法與注意事項.變式訓練可以有效地培養學生思維的靈活性和創造性,而歸納反思則可把解題的思想方法納入自己的知識系統,舉一反三,觸類旁通.
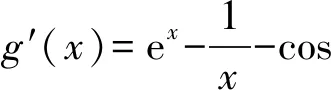
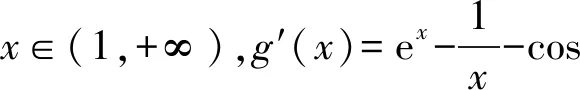


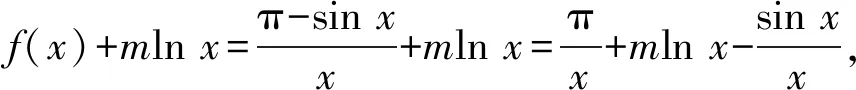
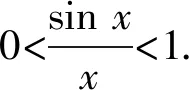
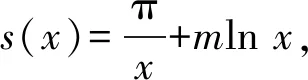
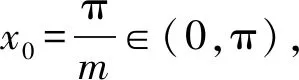
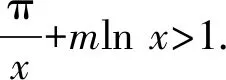

4 恒成立問題