一種風電聯軸器脹緊套強度校核方法

王習林，秦中正，胡偉輝，彭浩坤

(中國中車 株洲時代新材料科技股份有限公司，湖南 株洲412007)

0 引 言

脹緊套聯接是一種經過螺栓作用產生的抱緊力實現軸和機件聯接的裝置，具有結構簡單、承載大、過載保護及在沖擊載荷下性能優良等優點。在風力發電機組風電聯軸器中，脹緊套主要用來傳遞轉矩并提供過載保護作用，在整個風力發電機組中具有重要作用，所以對脹緊套強度的校核是保證風力發電機正常運行中極為重要的一環。脹緊套由外套、內套及螺栓組成，如圖1所示。

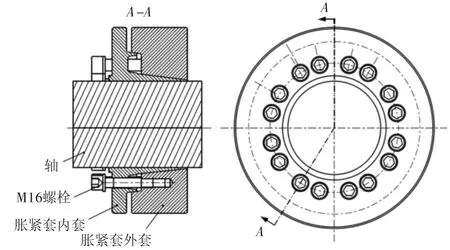
圖1 脹緊套與軸配合結果

承受內壓和外壓的脹緊套可簡化為受壓作用下的圓筒[1]，強度計算一般常用厚壁圓筒理論，對于脹緊套的內部應力為平均應力，其應力的分布無法通過計算準確獲得，而有限元分析的方式無法判定其有效性，因此本文對脹緊套進行理論計算及有限元分析的對比，與此同時對實際產品進行應力應變測試，驗證有限元分析的準確性，得出有限元分析與實際應力應變測試結果較為接近，有限元分析結果具有較高準確性的結論。

1 脹緊套強度理論計算

對于厚壁圓筒的脹緊套，最大應力發生在內表面[2]，因此強度校核只需校核內表面上的最大應力，且間隙越小，內表面上應力越大，故采用最小間隙進行計算。脹緊套內套除了承受內壓和外壓外，還承受扭轉切應力。

定義各參數如下：a為強度校核時部件外徑；b為部件內徑；p1為部件內徑所受內壓；p2為部件外徑處所受外壓；d1為軸與脹緊套內套接觸面直徑；d2為脹緊套內套與外套配合面的平均直徑；d3為脹緊套外套外徑；di為部件任意位置處的直徑；p1min為內套與軸配合面間隙最小時的壓強；p2min為內套與外套錐面處的壓強；d為螺栓直徑，此處為16 mm；T為單個螺栓擰緊力矩，取235 N·m；f為螺栓摩擦因數，取0.12；n為螺栓數量；F為總的軸向載荷；W為內外套接觸面正壓力；β為錐面半角；μ為內外套接觸面摩擦因數，取0.08；L為內外套接觸面長度；E為彈性模量；R為內套與軸最小間隙；Δp為消除間隙所需壓強。

根據第四強度理論（Miss屈服條件）公式[3]：

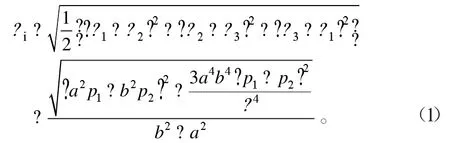
當ρ為內徑時，σi達到極大值，式（1）可簡化為

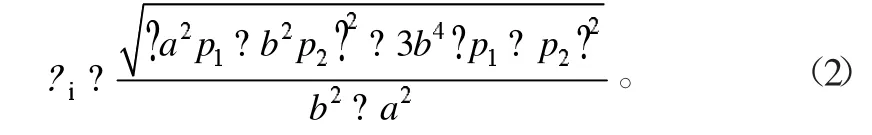
根據力學公式及消除間隙法計算公式：

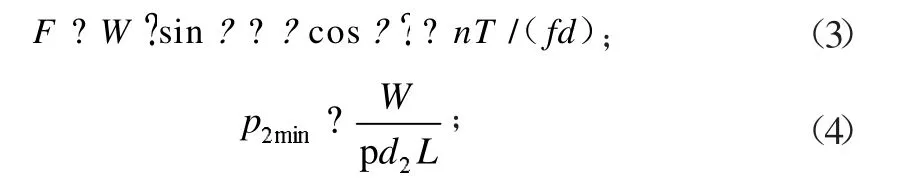
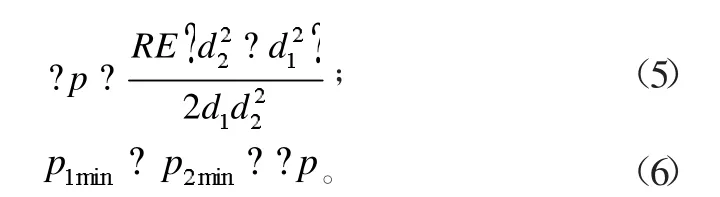
將各參數代入式（3）～式（6），可計算內外套接觸面處壓強p2min及內套與軸接觸面處間隙最小時的壓強p1min。

1）校核外套。外套圓錐面處受外壓為零，內壓為p2min，代入式（2），則外套最大應力為

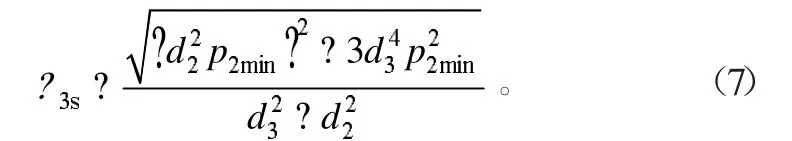
2）校核內套。內套所受外壓為p2min，內壓為p1min，代入式（2），則內套最大應力為

扭轉切應力計算公式為

式中：M為傳遞的轉矩；

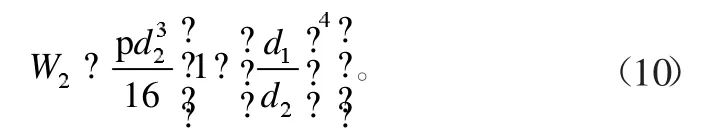
內套最大等效應力為

根據脹緊套各部件的強度校核，計算結果顯示，外套最大應力為638 MPa，內套最大應力為427 MPa，均小于屈服強度（650 MPa）。

2 脹緊套有限元分析

2.1 有限元建模及說明

該有限元分析運用ABAQUS6.11軟件進行計算，本文及分析中所采用單位系統為SI，即mm、N、MPa，脹 緊 套 內套、外套及軸的材料為42CrMo，所有單元采用C3D8R 單元模擬，單元數為82 105個，脹緊套有限元模型及網格模型如圖2所示。

圖2 脹緊套有限元模型及網格模型

2.2 載荷及邊界條件

該模型有4個接觸體，即脹緊套外套、脹緊套內套、螺栓、軸，四者之間均建立接觸關系如圖3所示。本分析中，脹緊套內外環及與軸的摩擦因數為0.08，螺栓摩擦因數為0.12。螺栓上施加預緊載荷（位移），對稱面分別施加對稱約束，脹緊套外套底部固定約束，如圖4所示。

2.3 計算結果及分析

2.3.1 加載載荷分析

在螺栓預緊力載荷作用下，將施加力的載荷等效為螺栓的位移載荷，通過測試和估算不同預緊力下脹緊套內套和外套間位移（A尺寸變化量），A尺寸位置如圖5所示，可得測試結果及估算結果如圖6所示。從圖6可知，計算提取的預緊力與測試結果誤差在10%以內，計算模型與實際較為符合，可以用位移載荷替代螺栓預緊力載荷。

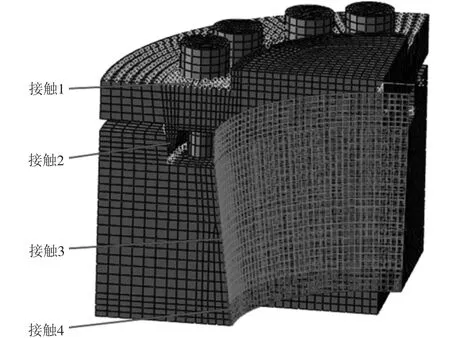
圖3 接觸關系示意圖

預緊力的計算根據公式:T=F·f·d，式中：T為緊固力矩；F為預緊力；f為螺栓摩擦因數，取0.12；d為螺栓直徑，該脹緊套選用螺栓為M16螺栓，等級為10.9級。當緊固力矩為235 N·m時，對應預緊力為122.4 kN。

2.3.2 螺栓預緊力為122.4 kN時的結構強度校核

根據2.3.1節計算結果，模型施加與螺栓極限預緊力122.4 kN等效的位移載荷，得到脹緊套各個部位的Mises應力分布如圖7～圖8所示。

從計算結果來看，脹緊套外套應力最大處為短錐面及螺紋口端面處，長錐面靠近螺紋口處局部，最大Mises應力654 MPa，脹緊套內套應力最大處在螺栓連接通孔端面處，為662 MPa，兩者最大Mises應力均略超過屈服極限（≥650MPa），局部存在部分塑性變形，而內套錐面最大應力為420 MPa，錐面上應力小于屈服極限，未發生塑性變形。參考《脹套圓錐過盈聯接的有限元數值分析》相關內容[4]，脹緊套錐面兩端局部塑性屈服符合該類產品應用實際情況，以不超過材料的抗拉強度（≥900 MPa）作為判斷依據，說明脹緊套強度滿足要求。

圖4 有限元載荷及邊界條件

圖5 測試內外套間隙位移示意圖

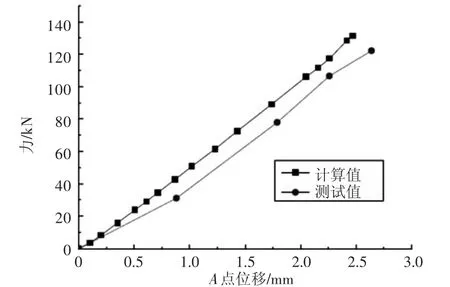
圖6 A點位移與螺栓預緊力關系計算值與測試值

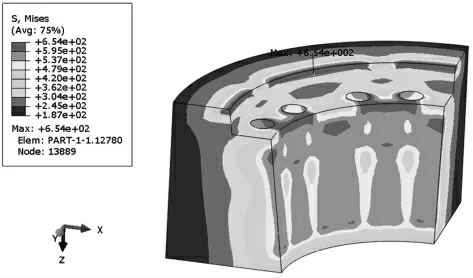
圖7 122.4 kN螺栓預緊力下，外套的Mises 應力分布

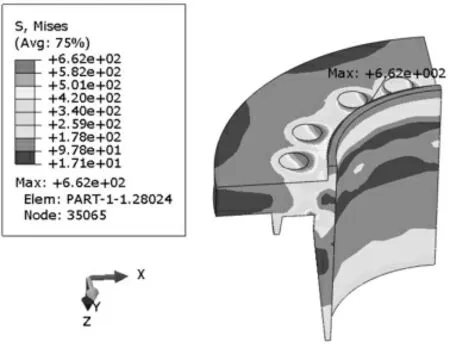
圖8 122.4 kN螺栓預緊力下，內套的Mises 應力分布

對比分析理論計算結果和有限元計算結果見表1，從表中可看出兩者在內外脹套錐面的最大應力較為接近。

提取脹緊套外套環向應力（距離外套底端42 mm處），其應力值大小如圖9所示，由分析可知，脹緊套外套在距離底端42 mm處環向應力大小較一致，約150 MPa。

表1 理論計算機有限元計算結果對比 MPa

3 脹緊套的應力測試

3.1 測試說明

3.1.1 應變片粘貼及測點布置

砂紙打磨聯軸器脹緊套試驗件貼片處，去除表面氧化物，使貼片位置平滑并用酒精清洗，要求打磨方向與應變片絲柵方向成45°角左右。貼片時在應變片上覆蓋聚乙烯薄膜并均勻滾壓應變片，擠出多余粘接劑和氣泡，貼片方向與主應力方向要求一致，貼片位置及圓柱坐標定義如表2和圖10所示（脹緊套外圓面布置2個單向應變片和1個應變花測點）。

3.1.2 試驗工況

通過轉矩扳手對螺栓施加相應大小的緊固力矩，分三階段依次加載：第一階段加載轉矩60 N·m；第二階段加載1500 N·m；第三階段加載235 N·m（相當于預緊力122.4 kN）。

脹緊套內外套均為42CrMo， 材料屈服強度為650 MPa，彈性模量E為207 GPa，泊松比μ為0.3。

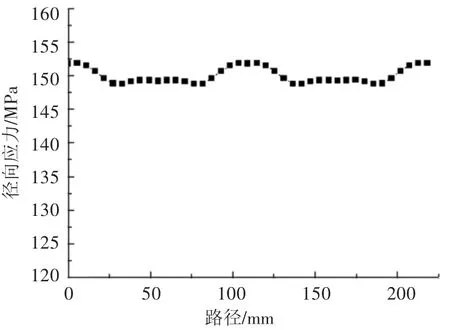
圖9 外套環向路徑的應力曲線

表2 測點位置說明

3.2 測試結果

測試時采集3組正常應變測試數據，先取每組數據中各載荷穩定時域曲線段的平均值，再取3組數據的算術平均值，得到表3所示應變測試結果。

在彈性變形范圍內，對表3中應變數據進行計算，得到各測點在被測工況下S1～S2單片測點應力值，以及E1應變花測點主應力值和等效應力值，計算方法如下：

單個應變片應力根據σ=Eε，E 為207 GPa，泊松比μ為0.3，計算結果如表4所示，由表4可知，在第三階段脹緊套外套圓周切向S1、S2、E1-0°的應力值分別為165.3 MPa、174.6 MPa、170.3 MPa，與有限元分析計算結果（150 MPa）接近。

圖10 貼片測點

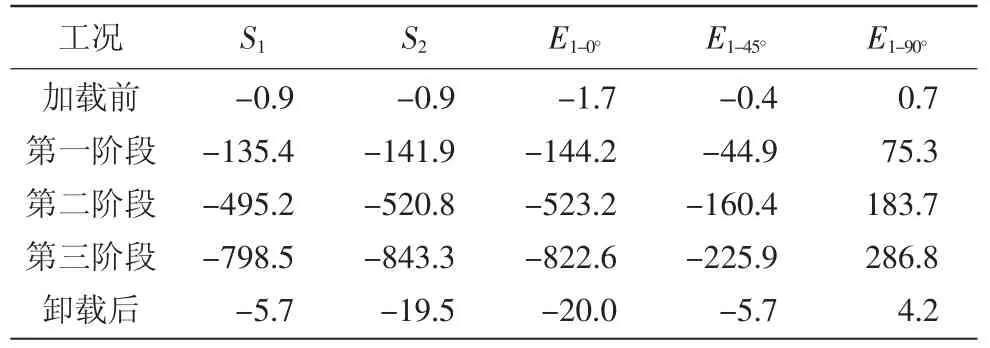
表3 各階段下各測點的應變測試結果 10-6

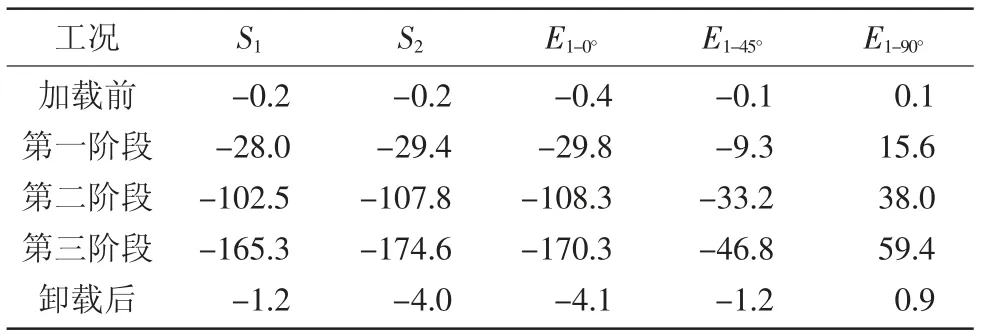
表4 各階段下各測點的應變計算結果10-6

4 結 論

1）對比分析理論計算結果和有限元計算結果表明，兩者在內外脹套錐面的最大應力較為接近，內套最大應力約420 MPa，外套錐面最大應力約650 MPa，略高出屈服強度，遠小于抗拉強度，在彈塑性變形階段，但錐面兩端局部塑性屈服符合該類產品應用實際情況。

2）對比分析實際產品距外套底端42 mm處的應力應變測試結果及有限元分析結果，表明實際測量結果與有限元計算結果接近，有限元分析結果有較好的準確性，可判斷本文對脹緊套的有限元分析方法可作為風電聯軸器脹緊套的強度校核方法之一。