拉曼光譜結合稀疏非負最小二乘算法用于混合物組分識別

顏凡 朱啟兵 黃敏 劉財政 張麗文 張恒

摘?要?拉曼光譜數據含有與被測物質組分相對應的指紋譜信息，是混合物組分識別的有效方法。傳統(tǒng)的拉曼光譜法用于混合物組分檢測時， 存在光譜特征提取困難、搜索比對算法性能容易受數據庫大小影響、識別精度難以保證等問題。針對此問題，本研究提出了一種基于稀疏非負最小二乘算法的混合物組分拉曼光譜識別方法。本方法將待識別的混合物光譜數據看作是各種純凈物光譜數據的線性表示;考慮到混合物組分數量相對于數據庫中純凈物數量具有稀疏特性，利用稀疏最小二乘算法獲得混合物光譜在純凈物光譜數據中的線性表示系數;并根據統(tǒng)計學中的2δ準則確定疑似組分;在此基礎上，利用迭代最小二乘算法并結合T檢驗方法，實現混合物組分的最終識別。本研究基于自建的500種純凈物拉曼光譜數據庫，對組分等體積比混合的19個混合物樣本和不同體積比的81個樣本進行了組分識別。結果表明，在等體積比情況下，本算法的查準率為90.24%，查全率為88.10%;對于不同體積比的混合物樣本，整體查準率為93.22%，查全率為83.65%， 表明此算法具有良好的穩(wěn)定性和準確度。

關鍵詞?混合物組分識別; 拉曼光譜; 稀疏非負最小二乘算法

1?引 言

混合物組分識別一直是分析化學中的難題。質譜和色譜分析法、化學實驗室法、固相萃取法等[1，2]組分識別方法雖然具有較高的靈敏度和精確度，但是無法滿足快速、簡便的檢測要求。近年來，基于拉曼光譜的檢測分析方法由于具有無損、非接觸、無化學污染、檢測時間短、檢測結果準確、重復性好、適用于大多數有機和無機化合物等優(yōu)點，得到了廣泛的應用[3～5]。然而，通過數學解析的方法提取拉曼光譜中包含的分子結構信息仍然具有很大的挑戰(zhàn)，特別是復雜的混合物光譜。目前，研究者已開發(fā)了各種化學計量學方法用于鑒定拉曼光譜中的成分。

搜索算法與數據庫相結合是解決混合物組分識別的一個重要方法。數據庫為解釋拉曼光譜提供強大的工具，隨著數據庫規(guī)模的增加，各種各樣的搜索算法應運而生。大量的搜尋方法是通過采用相關系數、歐幾里得距離、絕對值相關性和最小二乘法比較相似性，但是這些方法僅適用于檢測純物質[6]。在實際應用中，多組分的樣本是很常見的，因此，迫切需要開發(fā)鑒定混合物組分的算法。

Vignesh等[7]提出了一種混合物分析算法。該算法是首先通過搜索算法以生成樣本中可能存在的疑似物質列表，然后計算列表中每種物質的偏相關值，使用建立的廣義線性模型將偏相關值轉換為確定的成分在混合中真實存在的概率。但是該方法估計的概率的有效性取決于搜索算法的準確性，若搜索算法錯過多組分混合物中的一個或多個真實組分，則其估算的概率不可信。

馬靖[8]提出了一種基于激光拉曼光譜技術的二維分析方法，通過綜合分析特征譜線及若干特征譜線的強度比來測定混合溶液中存在的有機化合物，但特征峰的選取需要根據相關文獻資料及光譜標識規(guī)律確定。

Zhang等[9]通過自定義的匹配質量結合反向搜索對混合物進行定性分析，但匹配質量是根據兩種物質拉曼光譜的峰位與峰強定義的，其結果依賴于尋峰算法的準確性。黃培賢等[10]提出了一種子空間重合判斷法，將測得的混合物光譜視為向量，通過計算混合拉曼光譜與標準樣品數據庫拉曼光譜的子空間夾角，并依據子空間夾角變化確定混合物組分。Fan等[11]提出了一種基于卷積神經網絡（CNN）模型的混合物組分識別方法，得到了比傳統(tǒng)建模方法更優(yōu)的結果。針對由甲醇、乙腈、蒸餾水構成的三元混合物，能正確定性識別組分的最低體積濃度為4%。

綜上，現有的拉曼光譜混合物組分識別方法多依賴于拉曼光譜的譜峰特征提取，并逐一比對數據庫中物質與被測物質拉曼光譜特征的相似性。在實際測量中，當混合物中組分較多時，其拉曼光譜譜峰的重疊較為嚴重，給譜峰的特征提取與相似性計算帶來了極大困難。同時，當數據庫規(guī)模較大時，這種逐一比對的方法將極為耗時，并會產生較大的識別誤差[12]。

在拉曼光譜數據庫完備的情況下，混合物的拉曼光譜在數學上可視為拉曼光譜數據庫中拉曼光譜信號的線性表示。通常情況下，混合物組分相比于數據庫中的物質是稀疏的，換言之，混合物拉曼光譜數據在數據庫上的表示系數是稀疏的。近年來，信號的稀疏表示被廣泛的運用在信號處理等領域。本研究基于這種稀疏性質，提出了一種基于稀疏非負最小二乘算法（Sparse non-negative least squares algorithm，SNNLS）的混合物拉曼光譜識別方法。此方法通過計算混合物拉曼光譜數據在光譜數據庫中的稀疏表示系數，利用統(tǒng)計學中的2δ準則獲取較小的混合物成分疑似物質庫; 在此基礎上，利用迭代最小二乘算法和T檢驗方法，確定混合物的組分。基于自建的500種純凈物質數據庫，對組分等體積比混合物（19個樣本）和不同體積比的三元、四元混合物（81個樣本）進行了組分識別。結果表明，此算法具有良好的穩(wěn)定性和準確度。

2?算法原理與實驗

2.1?實驗儀器與實驗樣本

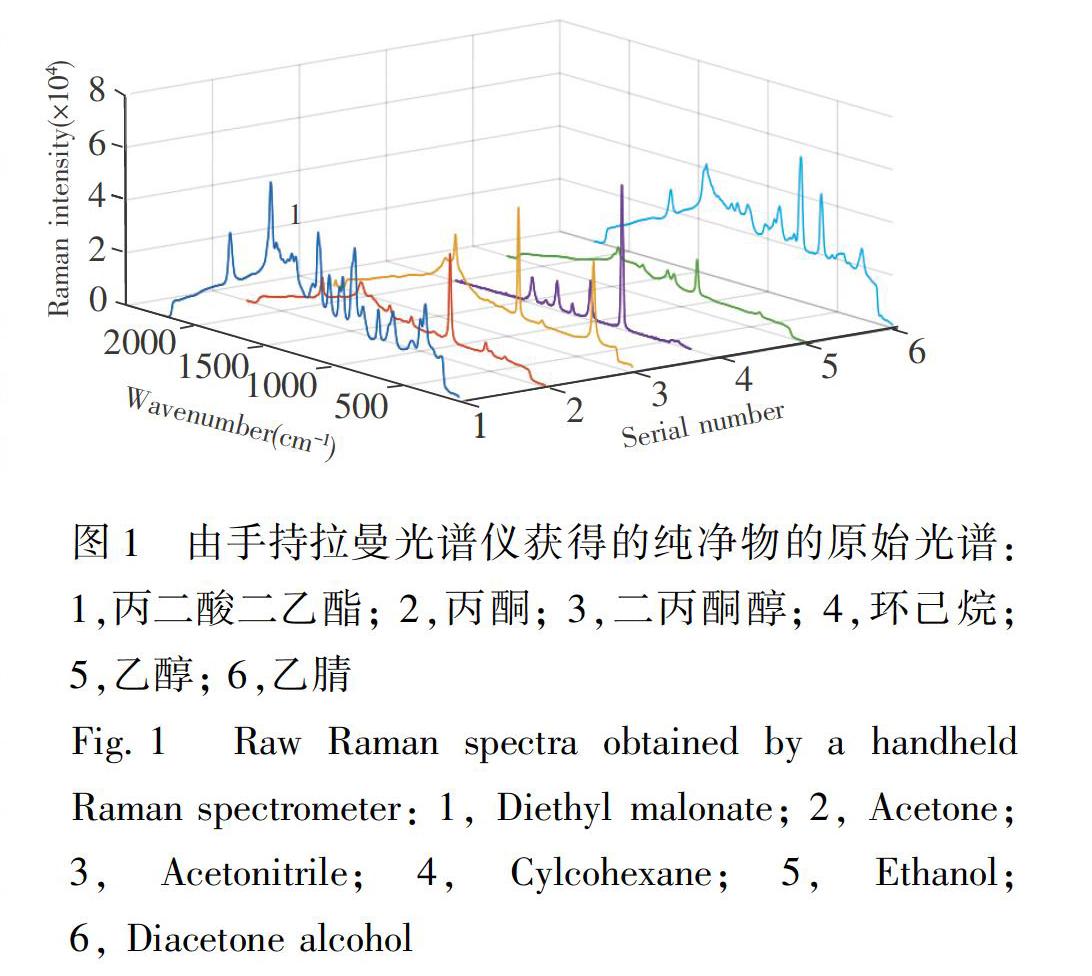
拉曼光譜數據用Finder Edge手持拉曼光譜儀（北京卓立漢光儀器有限公司）采集，激發(fā)源為785 nm激光器，激光功率350 mW， 光譜范圍150～2700 cm1，光譜分辨率為8～10 cm1 。 采集了500種純凈物在相同環(huán)境下的拉曼光譜數據，積分時間設置為1s，功率值約為70 mW，室內環(huán)境溫度約為23℃。500種純凈物數據庫由北京卓立漢光儀器有限公司建立，主要由常見化學物質和管制品組成。其中常見化學物質購于國藥集團化學試劑北京有限公司，純度為二級品，適用于重要分析和一般性研究工作; 管制品來源于公安機關，純度在98%以上。利用這500種純凈物的拉曼光譜數據（經過預處理）作為純凈物拉曼數據庫。在公共安全中，對一些有毒、有害、易燃易爆等物質的準確檢測至關重要。因此，本研究選擇了丙二酸二乙酯、丙酮、二丙酮醇、環(huán)己烷、乙醇、乙腈6種純凈物配制混合物，采集其拉曼光譜對算法進行驗證。

圖1為6種純凈物的原始光譜圖。由于這6種物質在常溫下物理狀態(tài)相同，都為無色液體，并且大部分為有毒有害物質，或易燃危險品（如乙醇），它們的分子結構比較類似，任意兩種物質的拉曼光譜都存在部分譜峰重疊情況（圖1）。考慮到純凈物譜峰之間的相互重疊現象，按組分等體積比混合配制了19個二元、三元混合物，表1為19個混合物樣本的組成; 考慮到各組分不同體積比混合對拉曼光譜數據的影響，配制了5種三元混合物樣本和3種四元混合物樣本，其中三元混合物樣本配制了9種不同的體積比，四元混合物樣本配制了12種不同的體積比，共81個樣本，部分樣本信息如表2所示。

2.2?SNNLS算法闡述

由于在實際環(huán)境中，混合物的組分可能多種多樣，要完全對其定性分析則需要龐大的拉曼光譜數據庫。SNNLS算法利用所有純凈物的全譜信息進行定性分析，避免了通過特征提取等降維操作改變數據結構、丟失有用信息的缺陷; 同時，SNNLS算法可獲取待識別物質在整個數據庫物質上的投影系數，克服了遍歷搜索方法存在的計算復雜度大的缺點。

設A∈Rm+n+為所有純凈物光譜數據構成的非負矩陣（m為光譜維數，n為純凈物樣本個數），則對于任意一個待識別混合物光譜y∈Rm+， 可由純凈物光譜矩陣A線性表示，其表示系數為向量x，即y=Ax。 x向量中各分量xi，i=1， 2， … n的大小與待識別物質中所含純凈物的濃度相關，在純凈物數據庫完備且數量較大的情況下，表示系數向量x是稀疏非負的。因此，本研究構造一個一范數稀疏非負約束方程，求解表示系數向量x：

minf（x）=‖Ax-y‖2+λ‖x‖1（1）

s.t.?xi≥0

其中，xi表示待識別光譜y在第i個純凈物下的表示系數。λ為稀疏懲罰因子，用于控制解向量x的稀疏性，其值越大，相應的解x越稀疏，本研究設置稀疏懲罰因子λ=n100（其中n為光譜數據庫樣本總數）。

將方程（1）轉換為無約束的對數障礙函數ni=1lnxi， 以方便求解：

minF（x）=‖Ax-y‖2+λni=1xi-Δnni=1lnxi（2）

其中，Δ=‖Ax-y‖2+λ‖x‖1-（-（Ax-y）T（Ax-y）-（Ax-y）Ty）， Δ越趨近于零， 代表此時的解x越靠近最優(yōu)解。隨著x逐漸向最優(yōu)解靠近， Δ逐步減小，相應的懲罰項-Δnni=1lnxi會隨著解x逐步逼近最優(yōu)解而趨近于零 [13]。對方程（2）的求解可采用牛頓內點法，算法的具體步驟如下： 步驟（1）對于待測光譜y和已知的純組分光譜數據庫A，設定初始解x1=（1，1，...，1）n×1， 循環(huán)次數初始化為k=1， 初始步長α=1，步長縮減因子s=0.5，控制參數c=0.5; 步驟（2）?若Δ<10-3，則退出循環(huán)，并輸出xk， 否則通過牛頓法確定迭代方向dxk=-F'（xk）F″（xk）; 步驟（3）?若步長α滿足F（xk+αdxk）≤F（xk）+αcF（xk）dxk，以及xki≥0 （i=1，2，...，n），則轉步驟（5）， 否則轉步驟（4）; 步驟（4）?令α=s·α，轉步驟（3）; 步驟（5）?令xk+1=xk+α·dx， k=k+1， 轉步驟（2）。

2.3?混合物組分的確定

相比于實驗室用高精度拉曼光譜系統(tǒng)，手持式拉曼光譜儀的測量環(huán)境難以控制，且儀器的分辨率普遍偏低，從而導致純凈物光譜存在較大的測量誤差。在純凈物光譜數據庫較大的條件下，利用SNNLS獲得的解向量雖然是稀疏的，但很難直接通過解向量的系數大小判斷物質是否存在。考慮到方程（2）獲得的表達系數xi是稀疏的，即在解向量x中， xi值較大的數量很少，可認為是一個小概率事件（相對于整個解向量x而言）。 借助于統(tǒng)計分布思想，將取值落在（μ-2δ， μ+2δ）外的xi認為是小概率事件，其中，μ和δ分別為向量x的均值和標準差。如果xi落在（μ-2δ， μ+2δ）， 則代表數據庫中的第i種物質為不相關物質，反之，將其歸為疑似物質。

通過上述方法獲得的疑似物質仍然偏多，為進一步確定疑似物質，本研究將疑似物質的光譜按照對應的系數xi，由大到小進行排列，得到B=（b1，b2，...，bL），其中，b1，b2，...，bL為數據庫A中L個疑似純凈物光譜。對前l(fā)（l=1， 2， … L）個純凈物光譜b1，b2，...，bl與待測樣本光譜y， 利用最小二乘算法求取擬合系數xl1，xl2，...，xll， 并計算殘差Δl=y-b1xl1-b2xl2-…，-blxll， Δl∈Rm。 重復此過程，可得到不同基底下的擬合殘差序列Δl，l=1， 2， … L。T檢驗使用t分布理論來推斷差異發(fā)生的概率，從而比較兩列數據是否存在顯著差異。本研究對以上殘差使用T檢驗確定混合物的組分。按照順序依此計算兩兩殘差的P值，若P（Δl-1， Δl）<0.01， 則代表兩殘差之間有顯著差異。即相對于前l(fā)-1個疑似純凈物光譜（b1， b2， …， bl-1）所擬合的殘差序列Δl-l， 第l個疑似物質光譜bl的引入， 對擬合殘差有較大貢獻，應作為疑似物質保留; 反之，可認為第l個疑似物質對整體擬合誤差沒有貢獻，可排除。通過上述途徑，可進一步縮小疑似物質庫，實現對待測混合物的定性識別。

2.4?算法評價指標

對于混合物成分定性識別問題，查準率（Precision ratio， P）和查全率（Recall ratio， R）是最為常用的兩個性能指標，本研究采用這兩個指標評價算法的性能。P反映了檢測的準確性，其定義為所檢出的混合物中真實存在的組分占檢出組分總數的百分比; R反映了檢測的全面性，其定義為所檢出的混合物中真實存在的組分占混合物組分總數的百分比。其定義公式如下：

P=TPTP+FP（3）

R=TPTP+FN（4）

其中， TP為實際存在于混合物中并被檢測到的物質; FP為實際不存在于混合物中但被檢測到的物質; FN為實際存在于混合物中但未被檢測到的物質。

3?結果與討論

3.1?光譜預處理

由圖1可見，物質原始光譜中含有熒光背景和噪聲等干擾，影響混合物組分的正確識別。因此，在建立數據庫并應用檢測算法之前，需對原始光譜進行預處理，去除干擾成分。小波變換由于具有高低頻信號分離的特點，可在不丟失原信號重要信息成分的前提下，將原光譜信號進行濾化處理，消除噪音信息，重構出更加清晰的光譜特征，從而提高了信號的清晰度，為信號的預處理提供了更方便的條件。本研究利用連續(xù)小波變換和懲罰最小二乘函數擬合背景線，去除熒光背景和噪聲[14]。選取墨西哥帽小波作為母波，其數學表達式如下：

Ψ（x）=23π

14（1-x2）e

x2/2（5）

圖2A為S20樣本在9種不同體積比下的拉曼原始光譜圖，可見含有較強的熒光背景; 圖2B為背景校正后的拉曼光譜圖，可見通過連續(xù)小波函數和懲罰最小二乘法相結合的方法進行背景校正后，消除了熒光背景產生的基線對物質拉曼光譜的影響，保留了光譜的有用信息。

3.2?算法的優(yōu)勢

本研究通過制備的組分等體積比混合的混合物樣本（表1），對SNNLS和文獻[9]提出的RSearch-NNLS算法進行比較，具體的自由參數設置與文獻[9]一致，表3給出了具體的性能對比。RSearch-NNLS通過檢測光譜的峰強與峰位計算混合物光譜與純物質的相似度。由表3可見，RSearch-NNLS的FP指標較高，其查準率僅為70.59%; 而本研究提出的SNNLS算法中僅出現4例FP，查準率達到90.24%，查全率也相對提高了2.39%。上述結果表明， SNNLS算法采用光譜的全波段數據進行混合物組分識別，避免了通過尋峰以及重疊峰的分解可能出現漏峰，以及重疊峰分解不完全等對識別精度的影響。

3.3?數據庫的大小對算法的影響

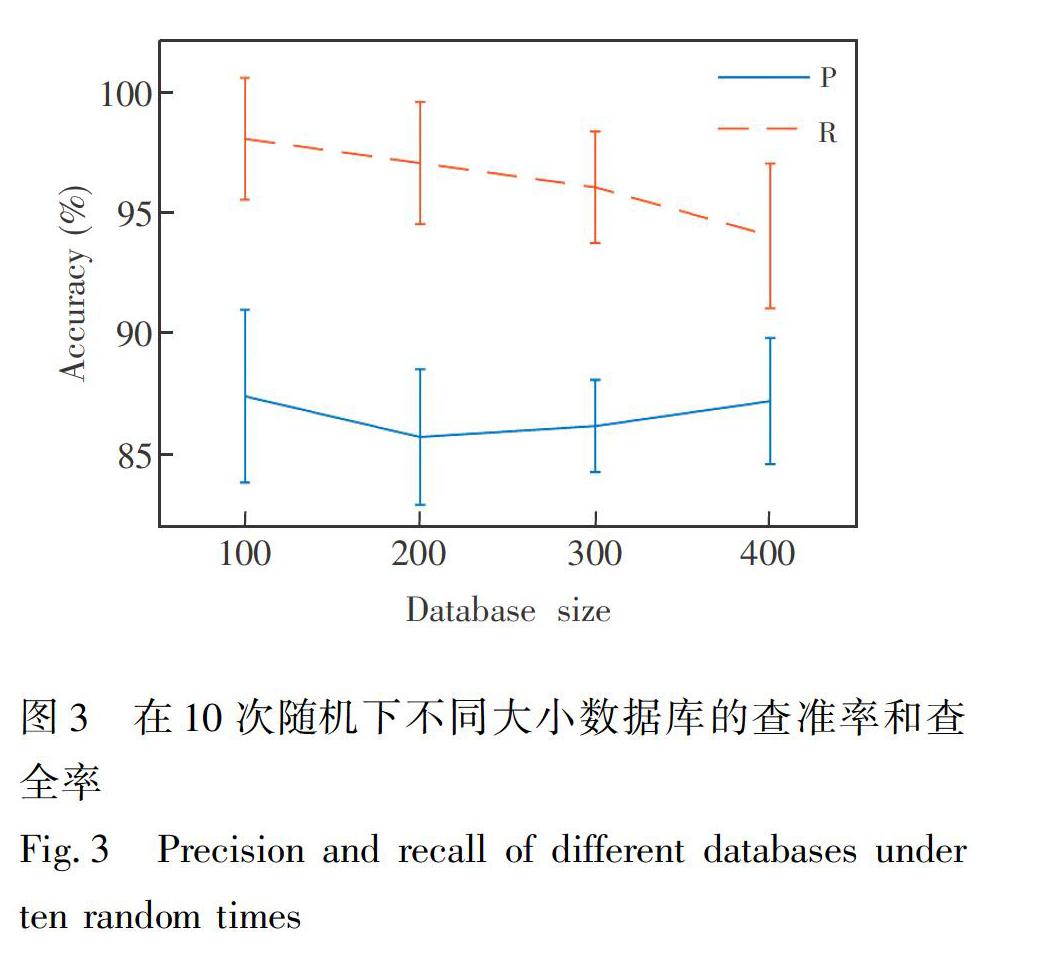
為了檢驗數據庫大小的變化對SNNLS算法的影響，從自建的500種純凈物的數據庫當中，隨機產生大小為100、200、300、400的子數據庫。為保證所產生的子數據庫相對于制備的混合物樣本具有完備性，本研究將含有制備混合物樣本的6種純凈物預先固定于子數據中，然后依次隨機抽取94、194、294、394種純凈物構成100、200、300、400的子數據庫，同一尺寸隨機抽取10次。根據隨機生成的子數據庫采用SNNLS依此對混合物進行檢測，結果如圖3所示，隨著數據庫規(guī)模增大，查準率的均值波動小于2%，最大方差為3.6%; 查全率的均值每次雖會逐步下降，但每次下降不超過2%，最低精度也大于90%，說明此算法在數據庫規(guī)模增加時檢測結果依然穩(wěn)定，具有良好的魯棒性和準確性。

3.4?數據庫不完備時算法的性能

在實際的檢測中，有時可能會出現數據庫不完備（數據庫中不含有混合物中部分組分）的情況。為了模擬這種情況，本研究從數據庫中人為刪除了一些存在于混合物中的組分，然后用SNNLS對混合物進行定性識別。如從數據庫中移除純凈物丙二酸二乙酯的拉曼光譜，對含有丙二酸二乙酯組分的混合物樣本S1、S4、S6、S11、S15、S16和S18（表1）進行識別，以檢驗算法的性能。采用同樣方法，依次檢測制備混合物組分的其它5種純凈物缺失的情況。

由表4可知，由于SNNLS算法需要在誤差范圍內盡可能地擬合待測樣本光譜，算法會搜尋到類似缺失項的光譜進行填充，這導致了大量FP的出現，降低了查準率，但平均查全率仍然維持在較高的水平（79.25%），這表明在數據庫不完備的情況下，所關注的混合物中的物質也可大部分被檢出。

3.5?混合物各組分體積濃度變化對算法的影響

考慮到混合物中各組分在不同體積比混合下對應的拉曼光譜具有差異性（圖2），而光譜數據的差異常會對各組分的識別產生重要影響。因此，本研究通過制備不同體積比的三元、四元混合物樣本（表2），對SNNLS和Rsearch-NNLS算法性能進行比較（表5），SNNLS算法中，丙酮、二丙酮醇的查準率和查全率要明顯優(yōu)于Rsearch-NNLS，但乙醇的FN指標相對較高（22）。其原因可能是乙醇的拉曼吸收峰相對較少，在其濃度較低時會出現漏檢的情況，導致查全率下降; 而RSearch-NNLS算法中，FN指標相對穩(wěn)定，不受各組分拉曼吸收峰多少的影響，這是因為RSearch-NNLS通過拉曼譜峰的峰強與峰位計算混合物光譜與純物質的相似度。從整體結果來看，相較于RSearch-NNLS，SNNLS的查準率和查全率分別提高了17.78%和3.04%。上述結果表明，SNNLS算法在保證解稀疏的前提下，通過調整數據庫中每種純凈物的系數對混合物光譜進行擬合，使殘差最小化，組分能正確定性識別與其所占的體積濃度和本身的拉曼吸收峰數量有關，總體上能正確定性識別組分的體積濃度在10%以上。

4?結 論

本研究提出了一種拉曼光譜中混合物的定性分析SNNLS算法，直接將全波段作為輸入信息進行定性識別，在保證解稀疏的前提下，通過調整數據庫中每種純凈物的系數對混合物光譜進行擬合，使殘差最小化，實現混合物的定性分析。利用500種純凈物構成的數據庫進行了實驗驗證，結果表明，在等體積比混合的19個混合物樣本中，算法的查全率為88.10%，查準率可達90.24%，與RSearch-NNLS相比，查全率提高了2.39%，查準率提高了19.65%; 在不同體積比的81個混合物樣本中，查全率和查準率分別為83.65%和93.22%，證明了此算法的穩(wěn)定性和準確性。此外，本研究也模擬了不完備數據庫下的混合物識別情況，結果表明，算法的平均查全率為79.25%，表明在數據庫不完備的情況下，混合物中的物質大部分也可被檢測到，證明算法具有較好的魯棒性。在混合物中組分的特征峰較少且濃度較低，或不同組分構建的混合物具有類似的拉曼光譜特征（峰位、強度）時，算法存在組分特征難以充分挖掘、性能降低的問題。如何提高上述情況下的定性分析結果，將是未來需要解決的問題。

References

1?LIU Bin， LIU Yun-Hu. Food Science and Technology， 2018， 43（6）： 317-321

劉 彬， 劉云虎. 食品科技， 2018， 43（6）： 317-321

2?WU Li-Sa， ZHAO Ming-Yue， GE Chang， CAI He-Qing， JI Ling-Bo， HU You-Chi， HU Jun. Tobacco Science & Technology，2018，51（4）：46-52

吳麗灑， 趙明月， 葛 暢， 蔡何青， 姬凌波， 胡有持， 胡 軍.煙草科技，2018，51（4）：46-52

3?Stckel S， Kirchhoff J， Neugebauer U， Rsch P， Popp J. J. Raman Spectrosc.，2016，47（1）：89-109

4?Penido C A F D， Pacheco M T T， Lednev I K， Silveira L. J. Raman Spectrosc.，2016，47（1）：28-38

5?Li Y S， Church J S. J. Food Drug Anal.，2014，22（1）：29-48

6?Shashilov V A， Lednev I K. Chem. Rev.，2010，110（10）： 5692-5713

7?Vignesh T， Shanmukh S， Yarra M， Botonjic-Sehic E， Grassi J， Boudries H， Dasaratha S. Appl. Spectrosc.，2012，66（3）： 334-340

8?MA Jing. Spectroscopy and Spectral Analysis，2014，34（7）： 1865-1868

馬 靖. 光譜學與光譜分析，2014，34（7）： 1865-1868

9?Zhang Z M， Chen X Q， Lu H M， Liang Y Z， Fan W， Xu D， Zhou J， Ye F， Yang Z Y. Chemometr. Intell. Lab. Syst.，2014，137： 10-20

10?HUANG Pei-Xian， YAO Zhi-Xiang， SU Hui， SUN Kuo. Journal of Instrumental Analysis，2013，32（3）：281-286

黃培賢， 姚志湘， 粟 暉， 孫 闊.分析測試學報，2013，32（3）：281-286

11?Fan X， Ming W， Zeng H， Zhang Z M， Lu H M. Analyst，2019，144（5）：1789-1798

12?HU Zhi-Yu， WANG Qiang. Journal of Test and Measurement Technology，2016，30（5）： 400-405

胡志裕， 王 強.測試技術學報，2016，30（5）： 400-405

13?Koh K. Stanford University，2009： 59-66

14?Zhang Z M， Chen S， Liang Y Z， Liu Z X， Zhang Q M， Ding L X， Ye F， Zhou H. J. Raman Spectrosc.，2010，41（6）： 659-669

Identification of Mixture Components Using Sparse Non-Negative

Least Squares Algorithm Base on Raman Spectroscopy

YAN Fan1， ZHU Qi-Bing*1， HUANG Min1， LIU Cai-Zheng1， ZHANG Li-Wen2， ZHANG Heng2

1（Key Laboratory of Advanced Process Control for Light Industy，

Ministry of Education， Jiangnan University， Wuxi 214122， China）

2（Beijing Zhuoli Hanguang Instrument Co. Ltd.， Beijing 101102， China）

Abstract?Raman spectral data contain fingerprint spectral information corresponding to the components of the measured substances， which is an effective method to identify the components of mixtures. The traditional mixture component detection methods based on Raman spectrum have some issues such as the difficulty in extracting spectral features， the performance of search and peak matching algorithms is easily affected by the database， and the recognition accuracy is difficult to guarantee. To overcome these problems， a method of mixture components recognition using Raman spectrum based on sparse non-negative least squares algorithm is proposed. In this method， the spectral data of the mixture to be recognized is regarded as the linear representation of the spectral data of all kinds of pure substances. Considering the sparse characteristic of the mixture components quantity relative to the pure substance quantity in the database， the linear representation coefficient of the mixture spectrum in the pure substance spectrum data is obtained by the sparse non-negative least squares algorithm. And the suspected components are determined according to the statistical 2δ principle. On this basis， the iterative least squares algorithm combined with the T-distribution test method is used to realize the final identification of the mixture components. The Raman spectral data of 500 pure substances are used to build a standard database for identification of the experimental sample of 19 mixtures with equal volume ratio of components and 81 mixtures with different volume ratio of components. The results show that the precision is 90.24% and the recall is 88.10% under the condition of equal volume ratios， and the precision is 93.22% and the recall is 83.65% under the condition of different volume ratios， which proves the good stability and accuracy of the proposed algorithm.

Keywords?Identification of mixture components;Raman spectroscopy;Sparse non-negative least squares algorithm

（Received 6 May 2019;accepted 15 November 2019）

This work was supported by the National Natural Science Foundation of China （No. 61775086）.